唯一性逻辑及其BP神经网络侦测*

张雨浓，邓健豪，金 龙，刘锦荣，殷勇华

(1.中山大学信息科学与技术学院，广东广州 510006;2.中山大学软件学院，广东广州 510006)

人工神经网络 (Artificial Neural Network，以下简称神经网络)是模拟生物神经系统的组织结构、处理方式和系统功能的简化系统［1］。神经网络作为一种并行的计算模型，能够在被建模对象的结构及参数均未知的情况下，通过训练，自适应地获取输入与输出之间的非线性映射关系［2］。由于其优秀的非线性映射、泛化、自组织及自我学习能力，神经网络已被广泛地应用于计算机科学技术、信息与通信工程、电气工程、人工智能、模式识别和控制工程等学科和领域［1，3］。

BP(Back Propagation)神经网络是由Rumelhart和McClelland等人于1986年提出的一种前向监督型神经网络［4］，由于其采用基于梯度下降思想的误差回传 (即BP)学习算法而得名。BP神经网络结构简单，具有较强的非线性映射能力，是目前应用最为广泛的神经网络模型及算法之一［1，4－5］。

本文创新地提出了唯一性逻辑，并展望了唯一性逻辑可能的应用前景。通过计算机数值实验验证，我们发现所提出的基于BP神经网络的模型可以准确有效地实现唯一性侦测。

1 唯一性逻辑

所谓唯一性逻辑，就是判断输入向量中是否存在唯一分量的逻辑。

定义 对于输入向量(x1，x2，…，xm)，若有且只有一个输入分量xk，使得xk≠xi，i∈{a|a=1，2，…，m且a≠k}，则称输入向量 (x1，x2，…，xm)具有唯一性，其中输入分量xk是唯一的。

例如，对于二值四输入的情况，若输入向量为(0，0，1，1)，则不具有唯一性;若输入为(1，0，0，0)，则第一个输入分量1是唯一的。

以下列举部分唯一性逻辑可能的应用前景。

首先，唯一性逻辑可以用于查找异常。例如，在生产工业中，需要对大量的同种类产品进行检验时，可以设定一系列的测试用例;对于这些测试用例，所有的产品都应具有相同的响应。若某一件产品的响应与其它产品的均不相同，通过唯一性检测，就可以马上定位出该产品，然后对其进行检查。

另外，若输入表示投票，则可以找出与众不同的一票。由于该票是唯一的、与众不同的，它代表了不同的意见，也许有着特殊的意义，需要作进一步探究。

总的来说，由于唯一性逻辑是新颖的，它的应用还有待开发。

2 用于唯一性侦测的BP神经网络

BP神经网络泛指那些采用误差后向传播算法的多层前向神经网络模型［1］。图1给出了一个三层结构的BP神经网络模型，包含输入层、隐含层和输出层。相邻两层的各个神经元彼此相连，且神经元之间的连接强度用连接权值来表示。当神经元将输入端的各个信号进行加权求和后，神经元的第二步工作就是通过激励函数对求和信号进行变换处理［1］，处理后的信号则为神经元的最终输出。

BP学习算法的思想是，依据神经网络实际输出与期望输出之间误差的负梯度方向，通过迭代，从后往前逐层地修正各层神经元之间的连接权值［6－9］，以使网络获得良好的逼近能力。

BP 学习算法的主要步骤为［10－11］:

1)初始化网络的权值和阈值;

2)计算网络各层输出向量和输出误差;

3)根据网络的输出误差，通过反向传播来修正权值和阈值;

4)重复2)和3)，直到符合特定条件。

2.1 训练算法

神经网络的训练算法是决定神经网络预测效率和收敛速度的关键［12］。传统BP训练算法存在着一些固有的缺陷［6－8］，例如易陷入局部极小点、学习收敛速度慢和网络结构难以确定等。为了克服传统BP算法的缺点，有许多新的改进算法和方法被提出［6－7，13］。这些方法包括增加动量项的 BP 学习算法、可变学习率的BP算法、弹性BP学习算法、共轭梯度法改进算法和Levenberg-Marquardt算法等。

本文实验采用了Levenberg-Marquardt算法，该算法同时具有梯度法和牛顿法的优点，是BP神经网络中最优越的算法之一［14］，具有训练速度快的特点。

2.2 网络结构

一般而言，具有一层隐含层的BP神经网络足够应付大多数应用［15］。相关理论研究证明［16－17］，一个以Sigmoid函数为隐含层神经元激励函数的三层神经网络可以逼近任意连续函数，具有强大的非线性映射能力。然而，当BP神经网络含有多个隐含层时，网络会变得过于复杂，有可能产生多个局部极小值以及导致较慢的收敛速度和较大的误差［15］。因此，本文采用单隐含层结构，单极Sigmoid函数作为隐含层和输出层的激励函数，理论上可以实现唯一性逻辑。

单极 Sigmoid 激励函数为［6－7］

其中，c为倾斜参数，其变化会影响Sigmoid函数的形状。由于该函数是全局可微的，这一优点在BP等梯度类学习算法中有着良好的效果。

由于输出层使用Sigmoid激励函数，这使得输出值为介于0到1的实数，因此，需通过四舍五入将最后输出值转换成整数0或1。

由于三层BP神经网络只有一层隐含层，因此，隐含层神经元数是比较重要的一个参数。计算机数值实验中，首先给定较小初始隐含层神经元数，构成一个结构较小的BP网络进行训练。如果在规定的训练次数内没有满足收敛条件，则停止训练，并逐渐增加隐含层神经元数，形成新的BP神经网络再重新训练。

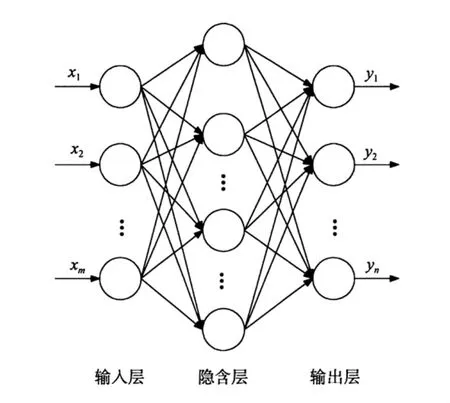
图1 一个三层结构的BP神经网络模型Fig.1 A 3-layer BP neural network model

3 三输入唯一性侦测实验

本文使用三层BP神经网络来实现三输入唯一性侦测。输入层神经元数为3，输出层神经元数为2。经过计算机数值实验，我们发现隐含层神经元数为5时网络收敛速度和训练效果最好。

3.1 训练样本

在本次实验中，所有样本都是二值的 (0或1)。唯一性侦测网络的输出为唯一输入分量的位置的二进制表示。

对于三输入的BP神经网络，有两个输出，代表四种情况，分别是:没有唯一性，第1分量是唯一的，第2分量是唯一的和第3分量是唯一的。所有8个训练样本及其含义如表1所示。

计算机实验的目标就是把网络训练到可以正确识别所有样本，即实现唯一性侦测。

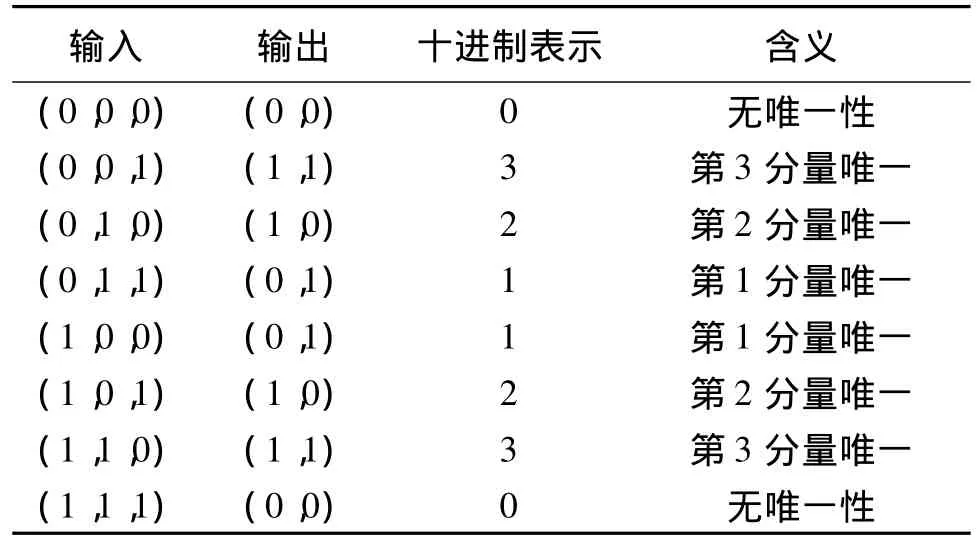
表1 三输入唯一性侦测网络的训练样本Table 1 Training examples for 3-input uniqueness detection network

3.2 实验结果

经过多次实验，我们发现，使用上述的三层BP神经网络结构和Levenberg-Marquardt算法，可以在短时间内成功地训练出用于唯一性侦测的三输入神经网络。

图2为三输入唯一性侦测网络在训练过程中的均方误差 (Mean Squared Error，MSE)变化图。具体而言，均方误差为测试值与目标值之差的平方的均值:

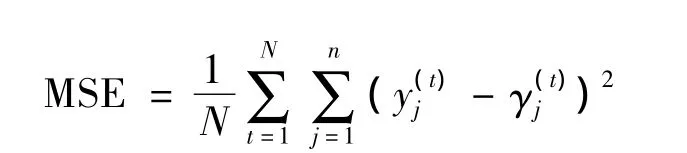
从图2可以看出，在第10次迭代完成时，MSE下降到目标误差值以下，训练结束。为了便于观察实验结果，将多输出向量转换成十进制的数字。从图3可以看出，训练完成后的网络对全部8个样本的测试结果与样本目标值完全一致。

4 四输入唯一性侦测实验

四输入的唯一性侦测网络的输入层神经元数为4，输出层神经元数为3。经过计算机数值实验，我们发现隐含层神经元数为15时网络收敛速度和训练效果最好。

4.1 训练样本

对于四输入的BP神经网络，有三个输出，代表五种情况，分别是:没有唯一性，第1分量是唯一的，第2分量是唯一的，第3分量是唯一的和第4分量是唯一的。表2为四输入的唯一性侦测网络的全部16个训练样本及其含义。

4.2 实验结果

图4为四输入唯一性侦测网络在训练过程中的MSE变化图，图5为训练后网络的测试结果。

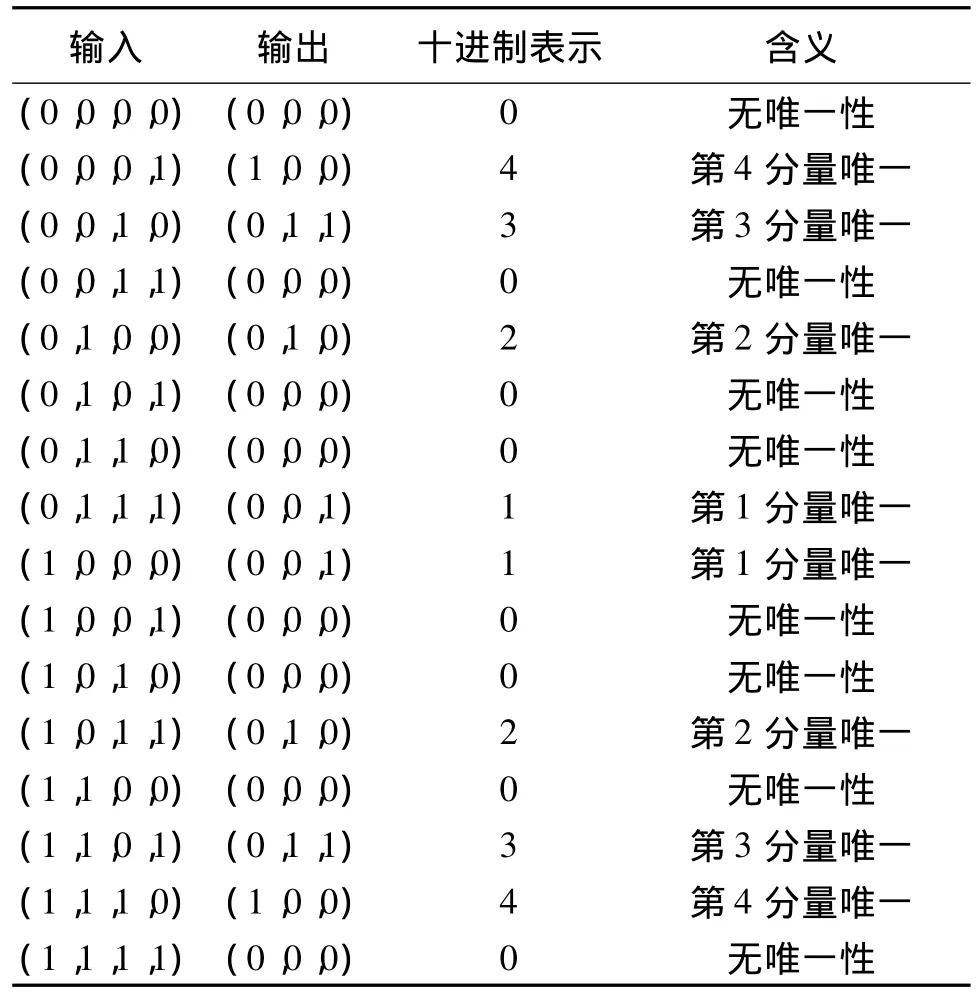
表2 四输入唯一性侦测网络的训练样本Table 2 Training examples for 4-input uniqueness detection network

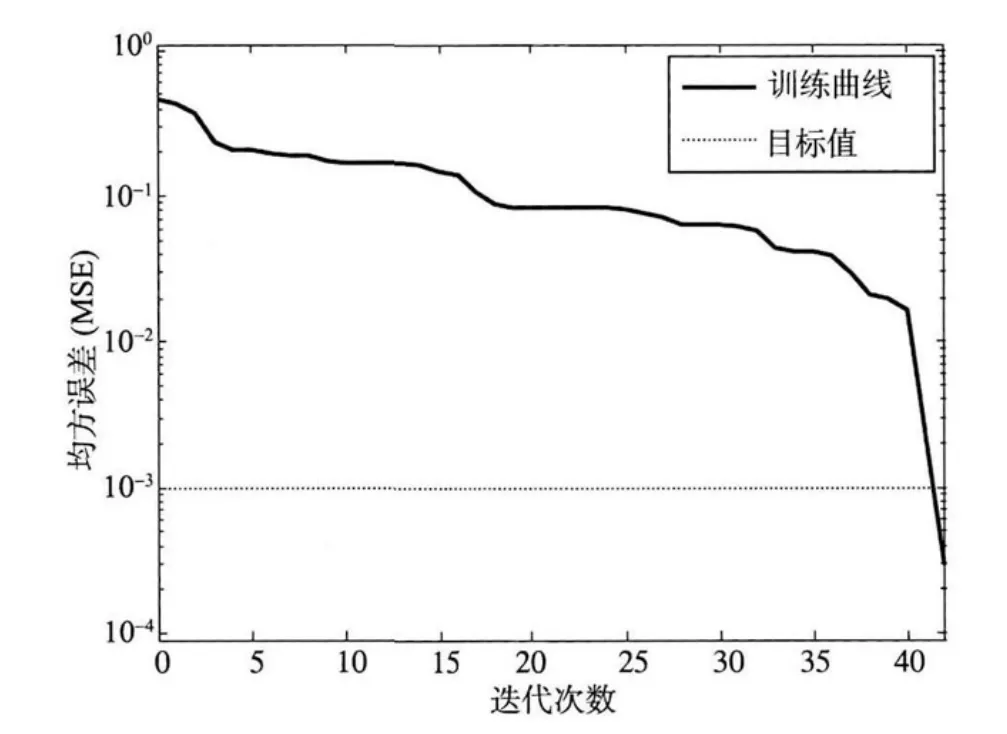
图4 四输入唯一性侦测网络的MSE变化图Fig.4 MSE curve of 4-input uniqueness detection network

从图4可以看出，在第42次迭代完成时，MSE下降到目标误差值以下，训练结束。从图5可以看出，学习完成后的网络对全部16个样本的测试结果与样本目标值完全一致。

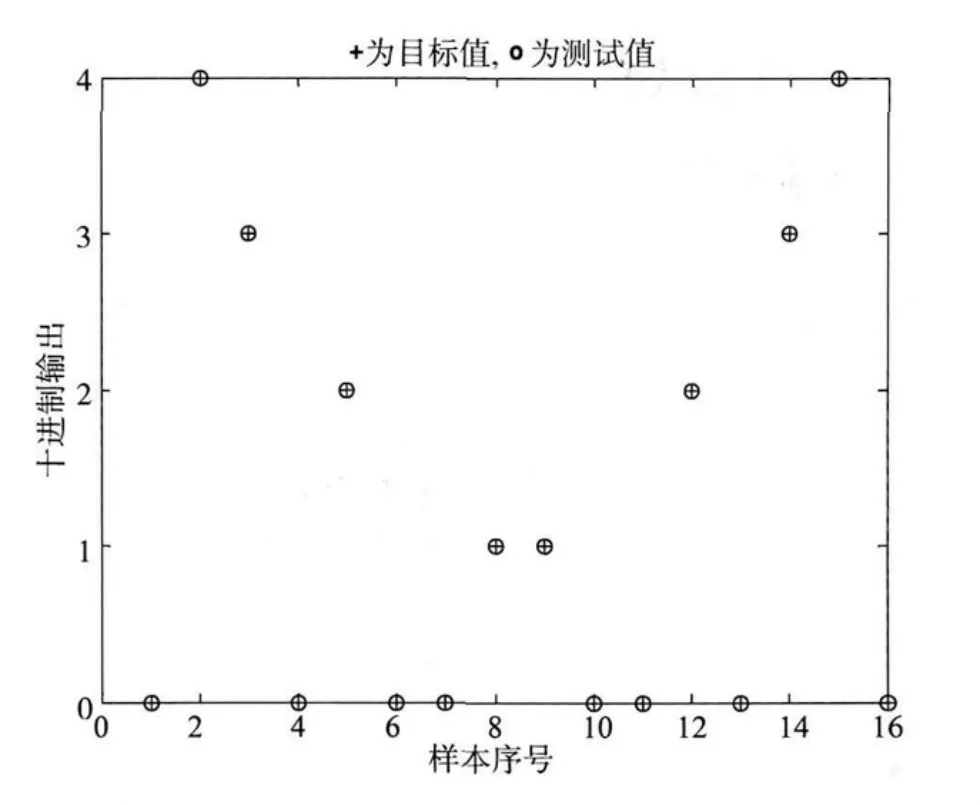
图5 四输入唯一性侦测网络的测试结果Fig.5 Results of 4-input uniqueness detection network

5 五输入唯一性侦测实验

五输入的唯一性侦测网络的训练方法与三、四输入的类似。表3为五输入的唯一性侦测网络的全部32个训练样本。

图6为5输入唯一性侦测网络在训练过程中的MSE变化图，图7为训练后网络的测试结果。实验结果显示训练完成后的五输入的网络对全部32个样本的测试结果与样本目标值完全一致。

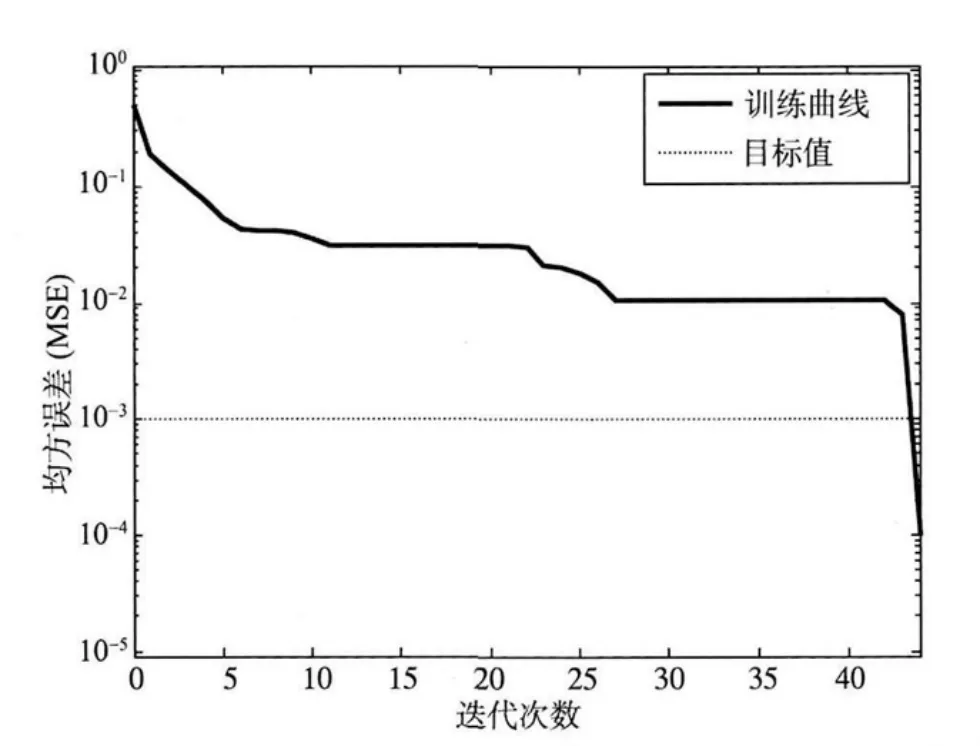
图6 五输入唯一性侦测网络的MSE变化图Fig.6 MSE curve of 5-input uniqueness detection network

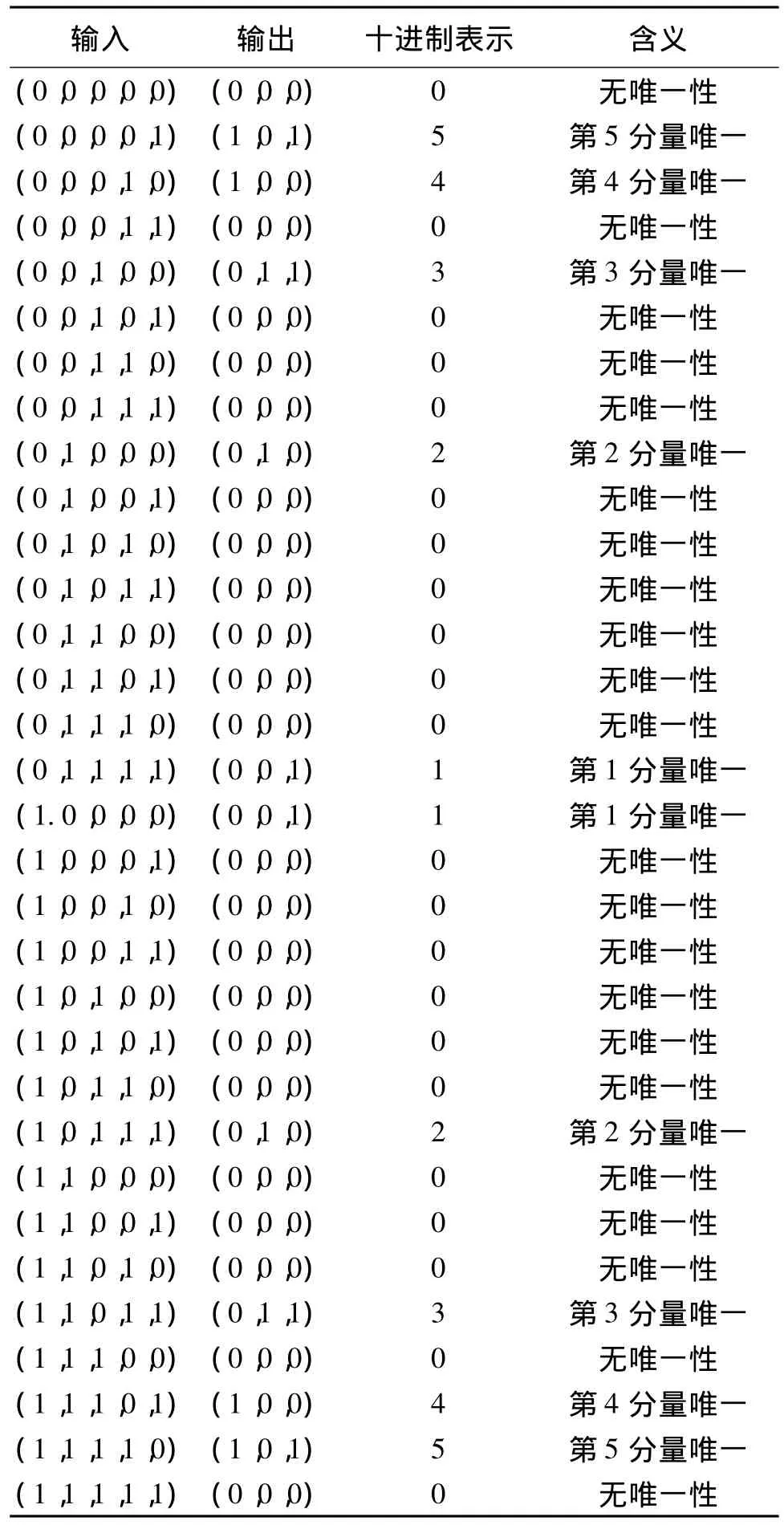
表3 五输入唯一性侦测网络的训练样本Table 3 Training examples for 5-input uniqueness detection network

6 结论

本文首先提出了唯一性逻辑的概念并给出其定义，指出了唯一性逻辑可能的应用前景。然后，通过计算机数值实验验证了BP神经网络实现唯一性侦测的可行性。实验证明，使用Levenberg-Marquardt算法可以快速、有效地训练出用于唯一性侦测的三层BP神经网络。

我们实现了三、四和五输入唯一性逻辑的BP神经网络侦测，为唯一性逻辑打下了理论和实验基础，有利于未来的实际应用以及推广到多输入的唯一性逻辑。

图7 五输入唯一性侦测网络的测试结果Fig.7 Results of 5-input uniqueness detection network

［1］张雨浓，杨逸文，李巍.神经网络权值直接确定法［M］.广州:中山大学出版社，2010.

［2］ZHANG Y N，LI W，YI C F，et al.A weights-directlydeter-mined simple neural network for nonlinear system identification［C］∥Proceedings of the IEEE International Conference on Fuzzy Systems，2008:455 －460.

［3］STATAKE T，KATSUMI M，NAKAMURA N.Neural network approach for minimizing the makespan of the general job-shop［J］.International Journal of Production Economics，1994，33:67 －74.

［4］RUMELHART D，MCCLELLAND J.Parallel Distributed Processing:Explorations in the Microstructure of Cognition［M］.Cambridge:MIT Press，1986.

［5］张雨浓，谭宁，李展，等.求解线性不定方程组所展现的BP与Hopfield类型神经网络的学习同质性研究［J］.中山大学学报:自然科学版，2010，49(2):1－7.

［6］张青贵.人工神经网络导论［M］.北京:中国水利水电出版社，2004.

［7］HAM F M，KOSTANIC I.Principles of neurocom-puting for science and engineering［M］.New York:McGraw-Hill Companies Inc，2001.

［8］成素梅，郝中华.BP神经网络的哲学思考［J］.科学技术与辩证法，2008，25(4):20－25.

［9］周政.BP神经网络的发展现状综述［J］.山西电子技术，2008，2:90－92.

［10］HAGAN M，DEMUTH H，BEALE M.Neural network design［M］.Beijing:China Machine Press，2002.

［11］HAYKIN S.Neural networks and learning machines［M］.Beijing:China Machine Press，2009.

［12］陈志坚，孟建熠，严晓浪，等.基于神经网络的重构指令预取机制及其可扩展架构［J］.电子学报，2012，40(7):1476－1480.

［13］高雪鹏，丛爽.BP网络改进算法的性能对比研究［J］.控制与决策，2001，16(2):167－171.

［14］苏高利，邓芳萍.论基于MATLAB语言的BP神经网络的改进算法［J］.科技通报，2003，19(2):130－135.

［15］FUH K H，WANG S B.Force modeling and forecasting in creep feed grinding using improved BP neural network［J］.International Journal of Machine Tools and Manufacture，1997，37(8):1167 －1178.

［16］HORNIK K，STINCHCOMBE M，WHITE H.Multilayer feed forward networks are universal approximators［J］.Neural Networks，1989，2(5):359－366.

［17］CHEN T，CHEN H.Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems［J］.IEEE Transactions on Neural Networks，1995，6(4):911－917.