镁基多孔材料准静态压缩行为与吸能特性研究

郝刚领，韩福生，王伟国

（1延安大学 物理与电子信息学院 材料物理研究所，陕西 延安 716000；2中国科学院 固体物理研究所 材料物理重点实验室，合肥 230031）

以高效能量吸收、高效热换、高效减振降噪等为特征的超轻多孔材料在航空航天、探月、铁路运输、汽车、环保、国防等领域具有重大的应用背景，成为金属材料研究最活跃的前沿领域之一［1－3］，两年一届的国际会议 “Porous Metals and Metallic Foams”，参会国家和参会人数的持续增加更是体现了对该类材料的重视。中国在2006年启动了国家重点基础研究发展计划（973）“超轻多孔材料和结构创新构型的多功能化基础研究”，2011年又实现了该项目的滚动立项（2011CB610300），这些都反映了中国对超轻多孔材料的重大目标需求和攻关决心。多孔材料作为一类兼有结构性和功能性的材料，具有非常广泛的应用背景，而降低多孔金属材料的密度，提高其功能性水平，是目前超轻多孔材料的重要发展方向之一。

目前，研究和应用最多的超轻多孔金属是铝基多孔金属材料，因为该类材料已有较完善的制备工艺（如：熔体发泡法，渗流法）和用于指导实际应用生产的性能数据库。而另一类超轻多孔金属材料－镁基多孔材料的研究还处于起步阶段，它的研究远较铝基多孔材料滞后，其中，性能研究的不足是其滞后的主要表现之一。究其原因，一方面起源于对镁基多孔材料的重视程度不够，另一方面受制于镁基多孔材料制备工艺的局限。但这种状况正在改变，以镁基多孔材料力学性能的研究为例，日本 Yamada等［4，5］对精密铸造法（石膏型渗流技术）制备的高孔隙率（一般＞90%）多孔AZ91D镁合金的准静态、动态压缩性能进行了系统考察，Wen等［6，7］也对低孔隙率（＜45%）、小孔径（微米量级）的多孔镁进行了初步研究。

本研究基于前期探索的镁基多孔材料的一种新型制备工艺［8］，对孔隙率在40%～80%，孔径在毫米量级内变化的多孔镁和多孔AZ91D镁合金的准静态压缩应力－应变曲线，损伤、破坏和能量吸收行为进行了系统考察，并探讨了相应的响应规律及其微观机制。

1 材料制备与实验方法

1.1 样品与测试装置

本实验选用工业纯镁和AZ91D镁合金粉末为基体，选用尿素颗粒为造孔剂。采用可去除填充颗粒的粉末冶金技术进行镁基多孔材料的制备。具体制备过程包括四个阶段，“均混＋压制＋脱溶＋烧结”，详细的工艺流程和制备参数见文献［8］。需要说明的是，制备中为了防止镁的氧化，脱溶在弱碱性水溶液中进行，烧结在流通的高纯氩（纯度＞99.999%）气氛下进行，同时，为了保证炉体内空气充分排净，高纯氩气流通之前，炉体先预抽真空（真空度不低于10－3Pa）。另外，合理控制烧结温度和保温时间非常重要，过高的烧结温度或过长的保温时间都易造成样品的氧化，降低样品的屈服强度，对样品屈服强度和烧结温度以及保温时间依赖关系的考察发现，烧结温度在600～630℃，保温时间在2.5h左右，产品的屈服强度最高，详情可参阅文献［8］。本实验中，样品参数变化范围为：孔径：0.5～2.0mm，孔隙率40%～80%。典型的镁基多孔材料形貌如图1所示。试样密度采用称重法测取，在计算相对密度时，取工业纯镁的密度为1.74g／mm3，工业AZ91D镁合金为1.80g／mm3。

准静态压缩是在Sans／CMT4204万能材料试验机上进行，该试验机由加载系统、测量系统及伺候系统组成，通过电子计算机来控制和数据的处理，实验精度±10－3。压缩采用的应变速率为2mm／min。试样的尺寸为φ20mm×20mm的圆柱体，试样尺寸比孔径大一个量级以上，能够代表材料的宏观力学性能。

图1 孔隙率为70%的多孔AZ91D镁合金的形貌 （a）孔径0.75mm；（b）孔径1.25mm；（c）孔径1.75mmFig.1 Morphology of the porous AZ91Dalloy with the porosity of 70%（a）pore size of 0.75mm；（b）pore size of 1.25mm；（c）pore size of 1.75mm

1.2 计算方法

通常用吸能本领（单位体积所吸收的能量C和吸能效率E）来表征多孔材料的吸能特性［9－11］，计算方法分别如下：

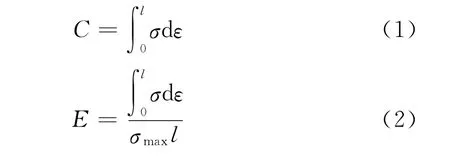
式中：σ为压缩应力，满足σ＝f（ε）；ε为应变；l为所考察的最大应变；σmax为位移σ后最大的压缩应力。

由式（1）和（2）式可知，吸能本领等于应力－应变曲线下所包含的面积，吸能效率则等于真实泡沫材料和理想泡沫材料（其压缩应力应变曲线为一水平线）压缩到相同应变时所吸收能量的比值，它实际上反映了材料吸能性能的优劣，对于工程设计来说是一非常重要的参量。

1.3 多孔材料单向压缩形变模型

理论和实验均已证明，多孔材料不论是弹性的、塑性的还是脆性的，压缩形变过程都可以分成三个部分：线性弹性区、塑性坍塌区或脆性破裂区（以下称之为平台区）和致密化区。不同的区域对应不同的响应函数。关于多孔固体压缩形变的本构模型较多，其中引用最多的是Gibson与Ashby的正六面体单胞模型［12］，借助于此模型，Gibson和Ashby运用量纲分析方法与标准梁理论，模拟了开孔泡沫材料孔变形与时效机制，得出了在单轴压缩条件下，开孔泡沫材料的屈服强度（或称坍塌强度与相对密度ρ＊／ρs之间的关系为：

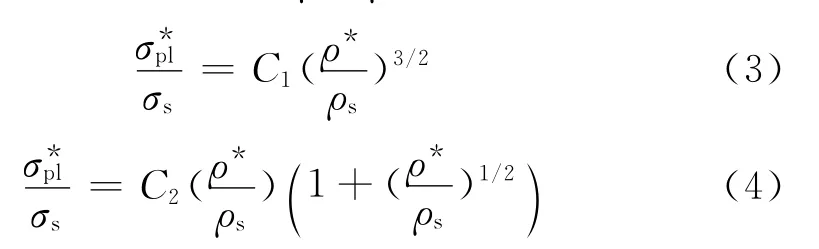
其中，C1和C2是与孔特征相关的常数，通过分析及实验验证，大多数开孔泡沫材料的C1＝0.3，C2＝0.23。式（3）一般只适用于相对密度低于0.3的多孔材料，而式（4）中由于包含了对相对密度的修正项，因此适合于相对密度高于0.3的多孔材料。

这种量纲分析的模型只依赖于所假定的变形模式，对所选取的胞体材料不敏感，如果把多孔样品中的孔洞看作球形，并且将胞壁简化为梁，那么胞体的受压问题也可以简化为梁的弯曲问题。

2 实验结果与分析

2.1 压缩应力－应变曲线特征及其微观机制

多孔纯镁和多孔AZ91D镁合金的压缩应力－应变曲线分别如图2和图3所示。可以看出，两种材料的应力－应变曲线具有如下特征：

图2 相对密度对多孔镁压缩应力－应变行为的影响Fig.2 Dependence of compressive stress－strain behavior of the porous Mg on the relative density

图3 相对密度对多孔AZ91D镁合金压缩应力－应变行为的影响Fig.3 Dependence of compressive stress－strain behavior of the porous AZ91Dalloy on the relative density

（1）与其他多孔固体材料类似，多孔镁和多孔AZ91D具有明显的三个阶段特征，即弹性区、脆性坍塌区（平台区）和致密区。线性弹性区所对应的应变值很小，均小于5%，该值与基体成分关系不大。在平台区，应力－应变曲线并非一水平线，而是锯齿状波动。当试样中所有孔壁都接触以后，即进入致密化区，应变增加导致孔隙的进一步减小以及基体的压缩变形。

（2）基体成分不同，力学性能明显不同，相同应变量下，多孔AZ91D的应力均高于多孔镁；基体的不同还影响到曲线形状的差异，多孔镁的曲线相对光滑，说明形变过程相对平稳，而多孔AZ91D在经历弹性段以后，曲线变得起伏很大，呈锯齿状，这主要是因为AZ91D镁合金的常温组织中，一般存在α－Mg和β－Mg17Al12两个相，其中β相本身很脆，且通常以类似网络状结构分布于α－Mg相的晶界处，使多孔AZ91D合金塑性很低，加上材料中孔洞边缘产生的应力集中，该脆性在多孔AZ91D的压缩中表现得更为突出。

尽管两种多孔材料在曲线形状上有所差别，但总体上说两者都属于脆性多孔金属，具有相同的脆性断裂机制。进入平台区之后，开始出现裂纹（如图4箭头所示）以及孔壁的断裂破碎，并伴随有碎块与基体的脱离。在应变量较小时，裂纹首先形成并集中于一些孔壁相对薄弱的区域，此时碎块和坍塌区也就仅限于一个窄小的区域内，与该区相邻的胞体仍然保持着弹性状态，随应变的增加，裂纹开始生长，并进而向整个基体内扩展，扩展的结果造成大量分离碎块的产生，进而在应力下的粉碎。由于基体较脆，裂纹的形成、孔壁的断裂以及碎块和基体的脱离都是突发式的。当应力超过某一值后，将有裂纹的产生以及碎体和基体的脱离，应力由此得到松弛而下降到较低值，随应变的增加，应力便会重新升高，直至新裂纹的产生而引起新碎体与基体的脱离。整个试样的破碎粉化即以这种方式重复下去，这也就是应力－应变曲线出现上下波动的原因，进入致密区后，分离的碎块在应力下完全粉化并和已粉化的粉体逐渐被压实而致密化。

图4 孔隙率为70.2%，孔径为1.25mm多孔AZ91D镁合金的横向压缩截面（a）应变量0.05；（b）应变量0.10Fig.4 Transverse compressive section of the porous AZ91Dalloy with the porosity and pore size of 70.2%and 1.25mm （a）strain of 0.05；（b）strain of 0.10

（3）压缩曲线上呈现出明显的两个屈服点，即上屈服点和下屈服点，分别对应于上屈服强度和下屈服强度。

2.2 相对密度和孔径对镁基多孔材料压缩性能影响

2.2.1 相对密度的影响

相对密度是多孔材料最重要的特征参数之一，几乎所有的压缩本构模型，都包含了相对密度对多孔材料力学性能的影响。图2和3分别给出了相对密度对多孔镁、多孔AZ91D压缩力学性能的影响，从图2和图3可以看出，相对密度对多孔材料的力学性能有显著影响，随相对密度的增加，压缩应力－应变曲线呈现以下的变化：（1）相同应变量下，曲线的应力逐渐增高；（2）弹性段的斜率变大。如果取应力－应变曲线上上屈服点所对应的应力作为多孔材料的屈服强度，则可得两种多孔材料的屈服强度随相对密度的变化关系，如图5和图6所示。

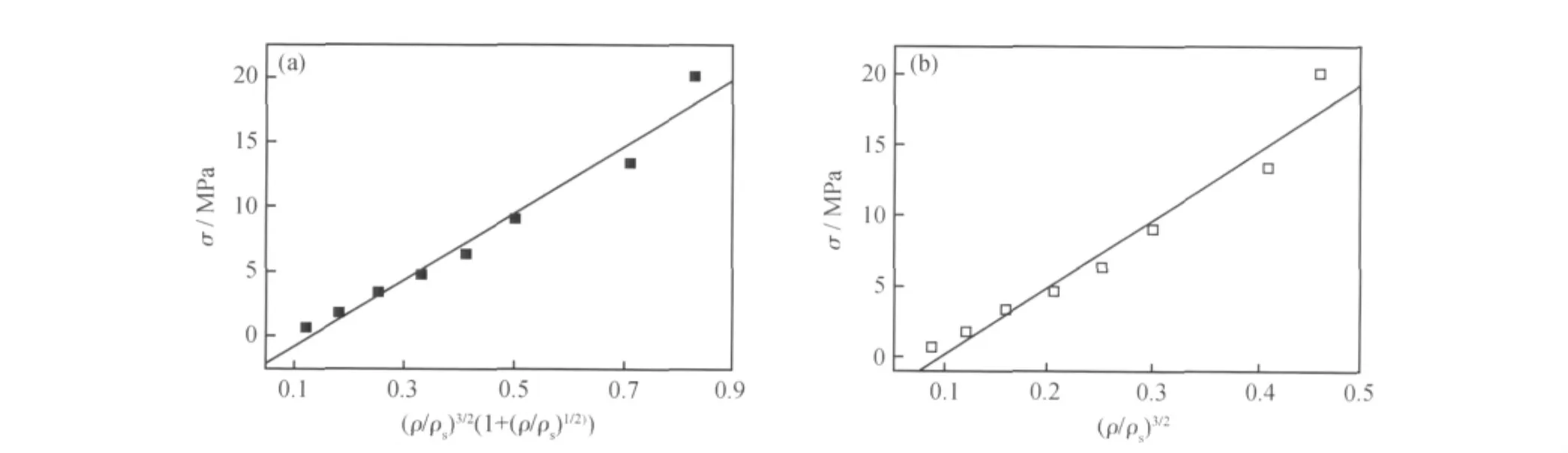
图5 多孔镁屈服强度与相对密度的关系 （a）按照公式（4）拟合；（b）按照公式（3）拟合Fig.5 Dependence of the yield strength of the porous Mg on the relative density（a）fitting according to the formula（4）；（b）fitting according to the formula（3）

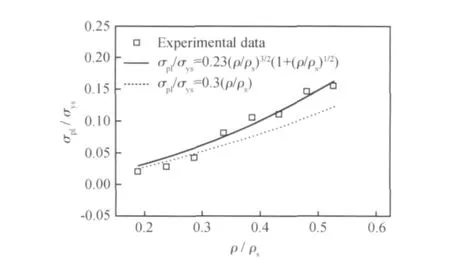
图6 多孔AZ91D镁合金屈服强度与相对密度的关系Fig.6 Dependence of the yield strength of the porous AZ91Dalloy on the relative density

对多孔镁来讲，它的屈服强度和相对密度之间的关系（见图5）基本符合关系式（4），但相对密度较大时偏离较大，数据也较分散；对于多孔AZ91D镁合金（见图6），它较好地符合标准梁模型，即在相对密度＜0.3时，其屈服强度和相对密度之间的关系满足关系式（3），在相对密度＞0.3时，满足修正后的关系式（4）。

2.2.2 孔径的影响

孔径是多孔金属材料的重要参数之一。研究结果表明，孔径对多孔镁和多孔AZ91D都没有明显的影响。如图7和图8所示，在相对密度基本相同的条件下，两种多孔材料的压缩应力－应变曲线基本重合，如取上屈服点所对应的压缩应力作为屈服应力，则不同孔径的多孔材料的屈服强度基本相同。

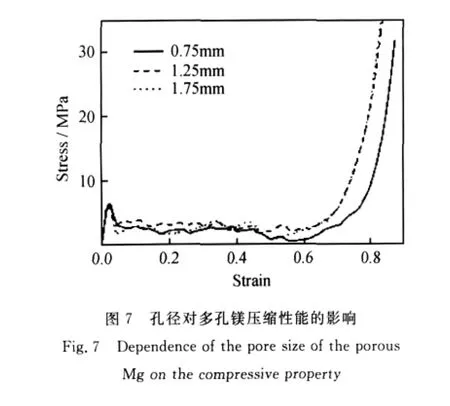
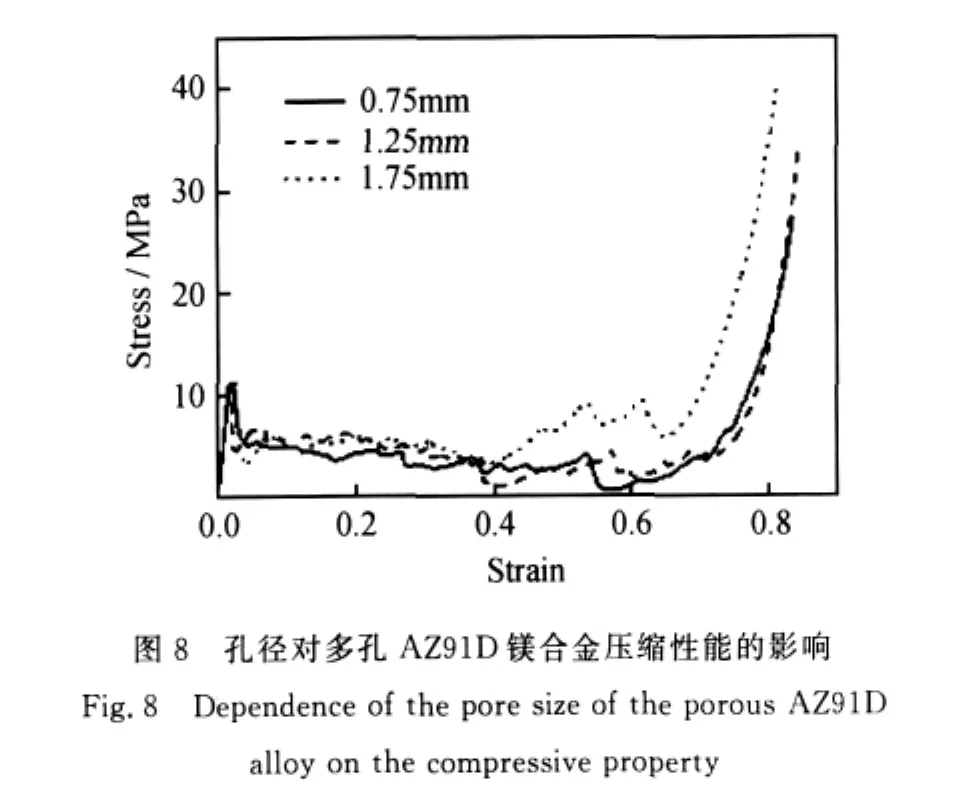
上述实验结果可用Gibson的正六面体单胞模型和梁理论来理解［12］：根据Gibson的模型，开孔材料的屈服强度σ与单胞孔边长l及孔边厚度t的关系为：

其中σys表示基体的屈服强度，又由于单胞模型的相对密度可表示为

这就说明，如果相对密度相同，虽然孔的大小（l）发生变化，但t／l比值却能基本保持不变，则屈服强度对孔径没有明显的依赖性。

2.3 能量吸收特征

2.3.1 吸能本领

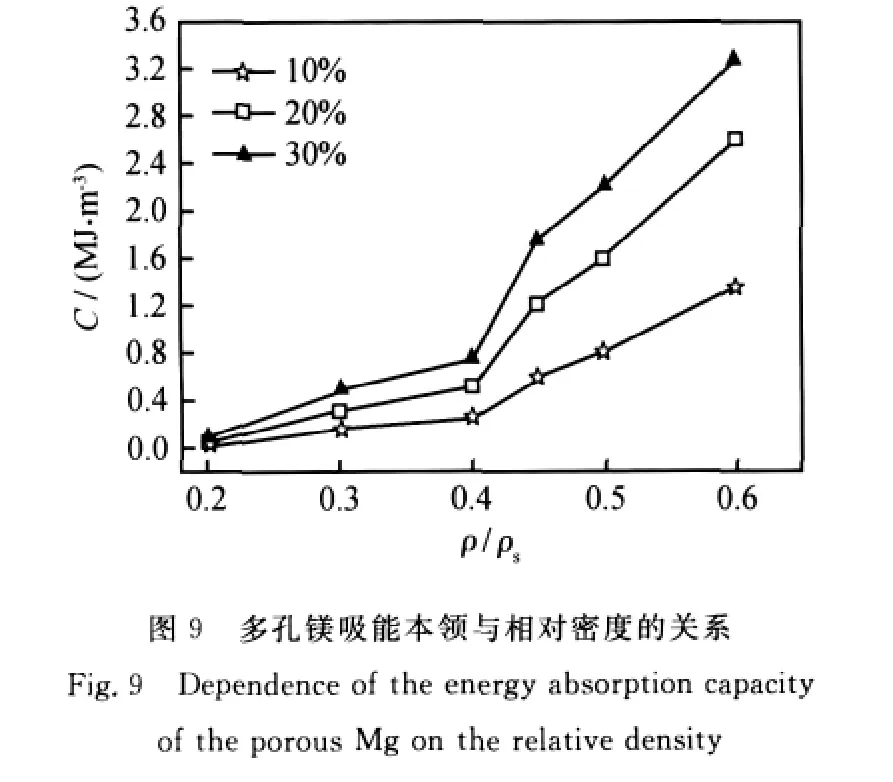
根据定义（见式（1）），材料吸能本领不仅与应力－应变曲线形状有关，而且和应变量l有关。为便于比较，分别测试了应变为0.1，0.2和0.3（均在平台区）时的吸能本领随密度的变化，如图9和图10所示，可以看出具有如下特征：

（1）多孔样品的吸能本领随相对密度的增加而增加；

（2）多孔AZ91D镁合金的吸能本领明显高于多孔镁，这与其基体具有较高的屈服强度有关。

一般来讲，多孔金属在压缩变形过程中的能量损耗主要由以下几个部分组成：

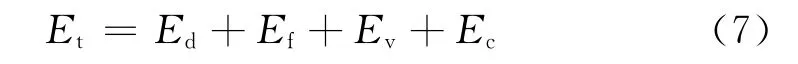
等式右边各项依次为：基体变形产生的能量损耗、孔壁接触时滑移摩擦产生的损耗、开孔中流体的黏滞性流动产生的损耗以及闭孔中气体不可压缩产生的损耗。显然，Ed和Ef对能量损耗的贡献最大。Ed主要取决于多孔材料的屈服强度和应变硬化率的大小，这也是多孔AZ91D镁合金具有较高吸能本领的原因。

2.3.2 吸能效率

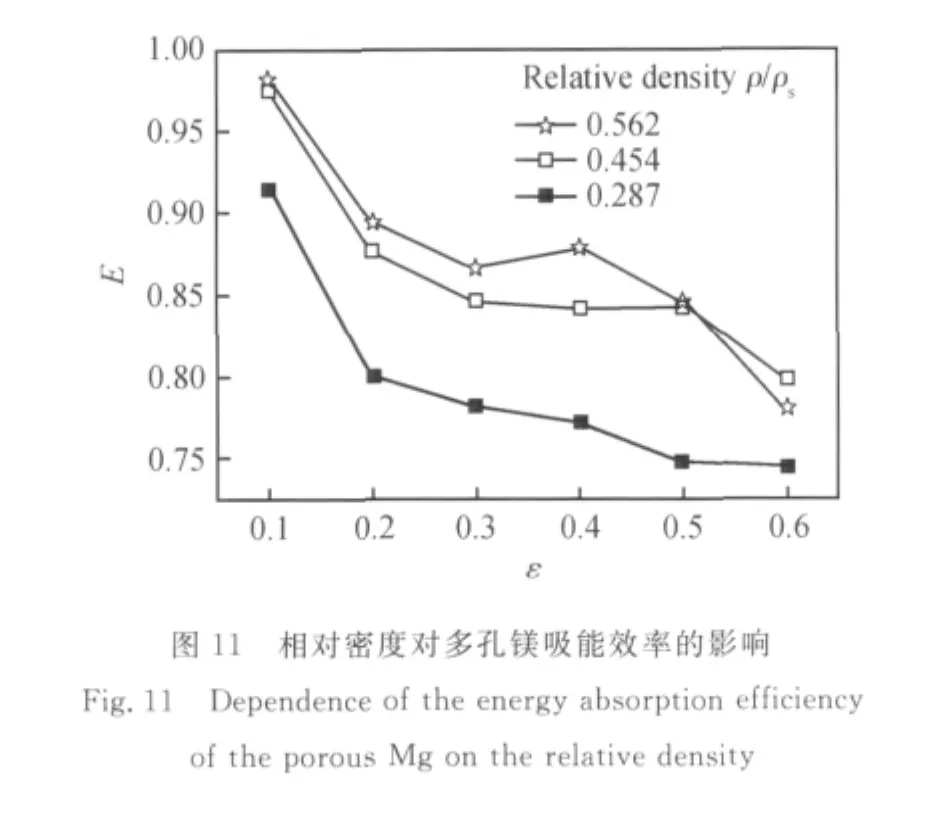
从式（2）可以看出，吸能效率大小取决于应力－应变曲线的形状，平台区越平坦，则吸能效率越高。对于多孔镁来说，它的压缩应力－应变曲线既不同于普通的塑性多孔金属，也不同于理想的吸能材料，存在明显的上屈服点和下屈服点，且下屈服点的应力远低于上屈服点的应力。因此，仅以平台区计算材料的吸能效率，即从下屈服点到致密化起点之间的区域，如图11和图12所示。可以看出，多孔纯镁和多孔AZ91D镁合金都具有较高的吸能效率，在所讨论的范围内，都大于0.6。随应变量增加，吸能效率逐渐下降。随相对密度增加，多孔纯镁吸能效率逐渐增加，但多孔AZ91D镁合金却起伏较大。造成这种现象的原因是多孔AZ91D镁合金压缩应力－应变曲线波动较大。总之，多孔纯镁的吸能效率高于多孔AZ91D镁合金的吸能效率。

3 结论

（1）多孔纯镁和多孔AZ91D镁合金的压缩应力应变行为与一般多孔金属相似，由线性弹性区、平台区和致密化区三个区域组成，但其压缩应力应变曲线波动很大，具有脆性断裂特征。

（2）多孔纯镁和多孔AZ91D镁合金的压缩屈服强度和相对密度的关系符合Gibson－Ashby模型。

（3）多孔纯镁和多孔AZ91D镁合金吸能本领随相对密度增加而增加，相同条件下，多孔AZ91D镁合金的吸能本领高于多孔纯镁，而多孔纯镁的吸能效率高于多孔AZ91D镁合金。

［1］BANHART J.Manufacture，characterization and application of cellular metals and metal foams［J］.Prog Mater Sci，2001，46（6）：559－632.

［2］NAKAJIMA H，KANETAKE N.Porous metals and metal foaming technology［A］.Proceedings of 4thinternational conference on porous metals and metal foaming technology［C］.Kyoto：Japan Institute of Metals，2006.1－10.

［3］何德平.超轻多孔金属 ［M］.北京：科学出版社，2006.1－7.

［4］YAMADA Y，SHIMOJIMA K，SAKAGUCHI Y，et al.Compressive properties of open－cellular SG91AAl and AZ91Mg［J］.Materials Science and Engineering A，1999，272（2）：455－458.

［5］MUKAI T，KANAHASHI H，YAMADA Y，et al.Dynamic compressive behavior of an ultra－lightweight magnesium foam［J］.Scr Mater，1999，41（4）：365－371.

［6］WEN C E，MABUCHI M，YAMADA Y，et al.Processing of biocompatible porous Ti and Mg ［J］.Scr Mater，2001，45（10－19）：1147－1153.

［7］WEN C E，YAMADA Y，SHIMOJIMA K，et al.Compressibility of porous magnesium foam：dependency on porosity and pore size［J］.Materials Letters，2004，58（3－4）：357－360.

［8］HAO Gang－ling，HAN Fu－sheng，LI Wei－dong.Processing and mechanical properties of magnesium foam ［J］.Journal of Porous Materials，2009，16（2）：251－256.

［9］GENT A N，RUSCH K C.Permeability of open－cell foamed materials［J］.J Cell Plast，1966，2（1）：46－51.

［10］THORNTON P H，MAGEE C L.The deformation of aluminium foams［J］.Metall Trans A，1975，6（6）：1253－1263.

［11］MILTZ J，GRUENBAUM G.Evaluation of cushioning properties of plastic foams from compressive measurements［J］.Polymer Eng Sci，1981，21（15）：1010－1014.

［12］GIBSON L J，ASHBY M F.Cellular Solids：Structure and Properties［M］.2nd ed.Cambridge：Cambridge University Press，1997.175－235.