基于晶粒旋转的纳晶材料非均匀变形行为研究*
韩雪平,周剑秋
(南京工业大学 机械与动力工程学院,江苏 南京 210009)
0 引 言
纳晶材料由于其独特的力学性能而引起了国内外研究人员广泛的关注[1-2]。一般来讲,相对于粗晶材料而言,纳晶材料虽然具有高强度,但其延展性很低,这种低延展性在很大程度上影响了纳晶材料的工程应用。
最近的研究表明,纳晶材料中剪切带的形成和发展是导致其延性降低、材料过早断裂的主要原因。Ramesh 等人[3]发现了在纳米Fe 的压缩过程中观察到的剪切带产生和发展的现象。Wei 等人[4]对块状纳晶W 在准静态和动态载荷下进行了压缩测试,结果显示有局部剪切化现象出现,并且剪切局部化现象随着变形的增加而增多。Ma 等人[5]发现在纳米Cu 的拉伸过程中也存在剪切带产生和发展的现象。此外,朱荣涛等人[6]对粗晶与纳晶镍片进行了拉伸试验,结果表明,粗晶镍的塑性变形是均匀的,而纳晶镍的塑性变形表现出局部剪切带化。刘龙飞等人[7]对金属玻璃发生剪切失稳形成剪切带的行为进行了分析。
综合上述研究可以发现,纳晶材料中的剪切带化现象已经成为材料塑性变形中不容忽视的一种机理。迄今为止,剪切带的本构模型和剪切带的基本物理特性仍没有定论,急需通过更先进的试验方法和完美的理论模型来加以验证。
最近,基于晶粒旋转的几何软化机理,Ramesh 等人[8]提出了一种纳晶剪切带演化的本构模型,该模型很好地预测了纳晶材料内剪切带的发展及剪切带宽度的变化,但是他们没有考虑晶粒取向分布对剪切带演化的影响。
基于以上分析,本研究提出一个新的基于晶粒旋转的剪切带演化模型,同时考虑晶粒取向分布以及晶粒尺寸对剪切带演化产生的影响。
1 晶粒旋转的剪切带演化模型
1.1 扩散驱动的晶界滑移引起的晶粒旋转
目前,许多关于晶粒旋转的研究[9]均假设晶粒旋转的驱动力是晶粒的一个净扭矩,这一扭矩来自于周围晶粒间的与晶界角有关的晶界能的变化。
基于Raj 和Ashby[10]的扩散驱动晶界滑移理论,Moldovan 等人[11]研究了具有任意截面的柱形晶粒的旋转,其关于扩散驱动的晶界滑移引起的晶粒旋转示意图如图1 所示。
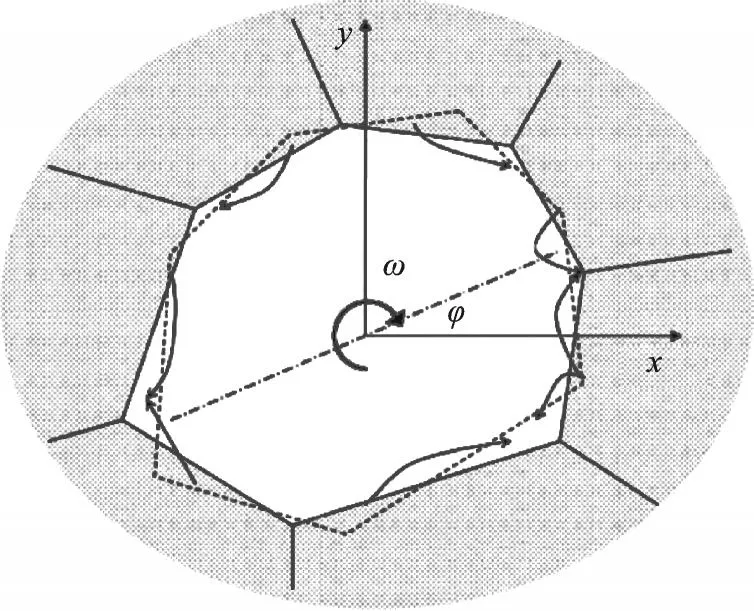
图1 扩散驱动的晶界滑移引起的晶粒旋转示意图
那么,对于一个给定的晶粒i 而言,作用于其质心的累积旋转扭矩为:

式中:h—圆柱晶粒的柱高,Li—各个晶界的截面长度,γi—长度为Li的晶界对应的晶界能,θi—长度为Li的晶界对应的晶界角,dγidθi—晶粒 i 的所有晶界累积而成的晶界能梯度。
众所周知,对于对晶体材料来说,晶界可以分成高角度晶界(θi15 °)和低角度晶界(θi<15 °)。虽然晶界的种类与材料的制造过程及材料本身的性质有关,但总体来说大部分的晶界都是高角度晶界。因此,本研究可以合理地假设,每个晶粒只有一个低角度晶界,其他的都是高角度晶界。Read-Shockley[12]公式很好地解释了低角度晶界的晶界能随晶界角的变化。根据Read-Shockley 公式,高角度晶界和低角度晶界的晶界可表示为:

其中:

式中:G—弹性剪切模量,b—伯格斯矢量,ν—泊松比,A—常数。
至此,通过量化表示晶粒的累积晶界能梯度,公式(1)中的累积扭矩公式可改写成:
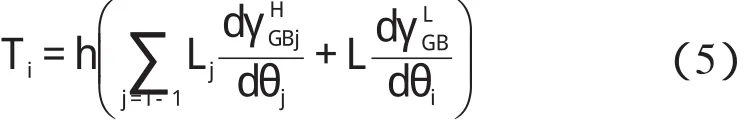
将式(2,3)代入式(5)中,经简化计算,可得晶粒旋转扭矩的简化表达式为:
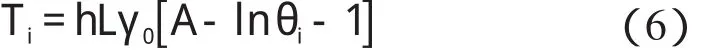
为了分析扩散驱动的晶界滑移引起的晶粒旋转,Moldovan 等人把晶粒旋转看作是一个粘性过程,提出了关于晶粒质心的角速度,即晶粒的旋转速度为(如图2 所示):

式中:ϕi—晶粒取向;M—在扭矩Ti作用下晶粒的旋转迁移率,并且这一迁移率与平均晶粒尺寸有很大的关系。
扩散驱动的晶界滑移引起的晶粒旋转的均匀化表述如图2 所示。
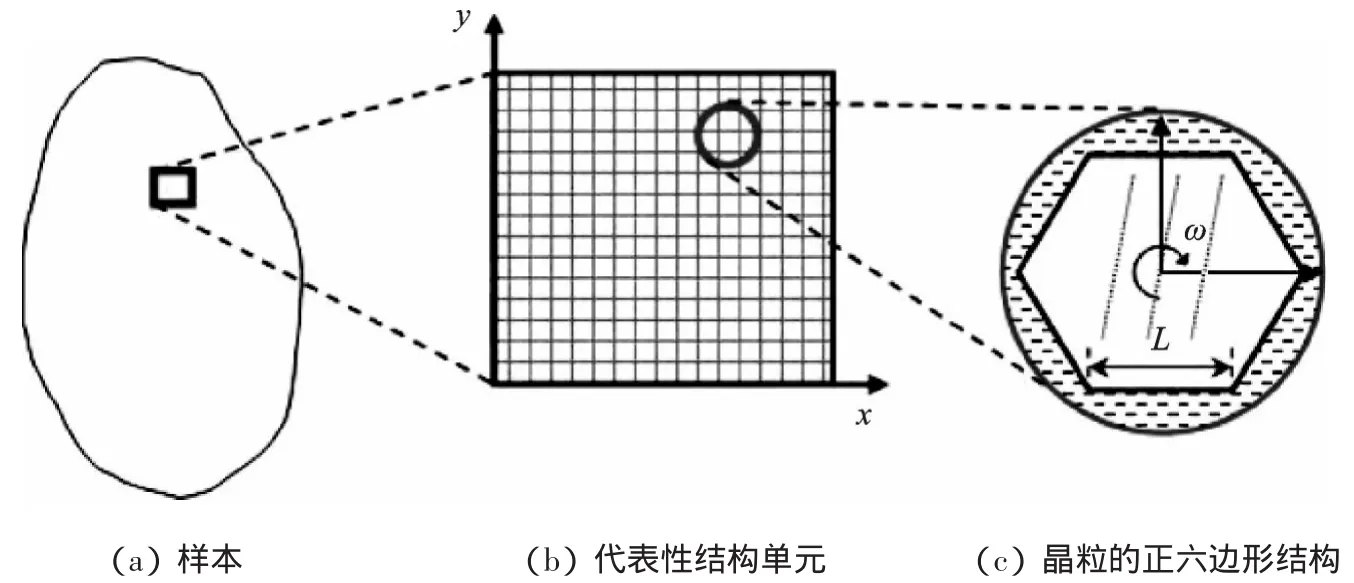
图2 扩散驱动的晶界滑移引起的晶粒旋转的均匀化表述
Moldovan 等人通过对旋转迁移率的不同表述,分别考虑了晶界扩散和晶格扩散对晶粒旋转的影响,并对多晶钯给出了一个特征长度dc=1.8μm。依据这个特征长度,当晶粒尺寸小于dc时,晶界扩散是晶粒旋转的主要机制;相反,当晶粒尺寸大于dc时,晶格扩散则起主导作用。
而对于纳米晶体材料(d<100 nm)来说,研究者可以认为晶粒旋转的主要驱动力来自晶界的扩散,但是,他们并没有考虑外来应力对晶界滑移和晶粒旋转所带来的影响。而Kim 等人[13]所利用的能量守恒方法,则考虑了外来应力对晶界滑移所造成的影响。
利用这一理论,本研究把外来应力对晶粒旋转的影响归结于对晶界滑移的影响,并且在Moldovan 模型的基础上重新定义了晶粒旋转的迁移率。
其迁移率可表示为:
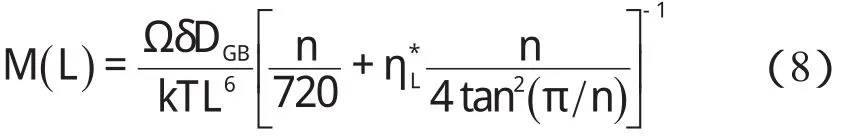
式中:η*L—基于Kim 等人的方法提出的一个定义粘度,可表示为:

式中:ηGB—晶界滑移的有效粘度,可表示为:

式中:n—晶粒的晶界数量,Ω—原子的体积,δ—晶粒周围晶界的扩散宽度(也就是晶界的宽度),DGB—晶界的扩散系数,L—晶界的长度,k—玻尔兹曼常数,T—相关的绝对温度。
将式(6,8)代入式(7),可得晶粒的旋转角速度为:
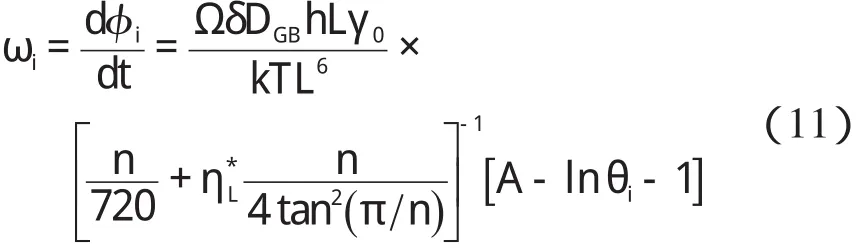
为了更简便地计算晶粒的旋转,本研究假设所有晶粒截面的形状都是n=6 的正六边形,该截面的正六边形结构如图2(c)所示;并设定晶界的长度等于晶粒的半径(L=d/2),柱形晶粒的柱高与晶粒尺寸相等(h=d),则式(11)可进一步简化为:
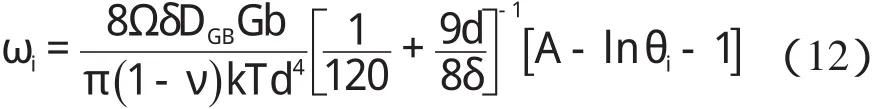
1.2 剪切带的演化
基于剪切带的特点以及晶粒旋转的理论,按照晶粒取向与剪切方向的差异,本研究将晶粒分成剪切带内容易发生滑移的软晶粒和剪切带外只发生扩散蠕变的硬晶粒。
为了描述剪切带的演化,本研究考虑了一个代表性结构单元,如图2(b)所示。在这一单元中含有N 个晶粒,其中有Ns个软晶粒,这里用一个软化因子来表示软晶粒的比例分数。
随着晶粒的旋转,软晶粒的数量不断增加,软化因子η也随之变化,软化因子能够反映这一结构单元内晶粒旋转的情况。进而软化因子的变化就形成了一个软化机制,这一软化机制产生了越来越多的晶粒取向趋向于剪切方向的结构单元,在外力作用下,就形成了剪切带区域(η=1),晶粒旋转导致的剪切带演化示意图如图3 所示。
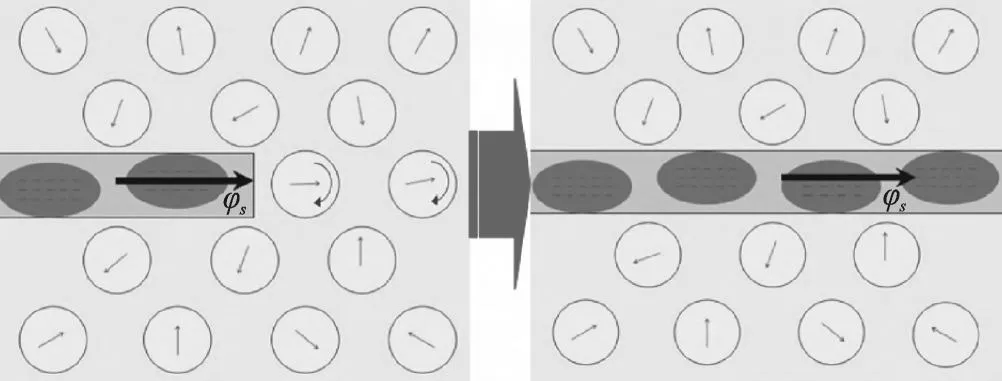
图3 晶粒旋转导致的剪切带演化示意图
因此,本研究就以软化因子的变化来描述剪切带的演化。
前面已经对单个晶粒的旋转进行了相应的分析,而这并不能表述整个结构单元内软化因子的演化,如图2(b)所示。为了进一步精确表述晶粒旋转引起的剪切带的演化,研究者必须将单个晶粒的旋转与软化因子的演化联系起来。
在此,本研究采用类似于Ramesh 等人提出的一个加权平均值方法,均匀化地表述整个结构单元的晶粒取向ϕ,进而建立了一个软化因子的均匀化演化机制。
那么,在整个结构单元内,所有晶粒的平均晶粒取向可表示为:

进一步地,本研究通过一个Delta 函数形式的补偿函数(式中:ϕs—剪切方向),对晶粒取向进行一个加权平均来计算软晶粒的比例分数(即软化因子)η,即:

则软化因子η的平均变化率可表述为:

进一步合并公式(12,15),可得:
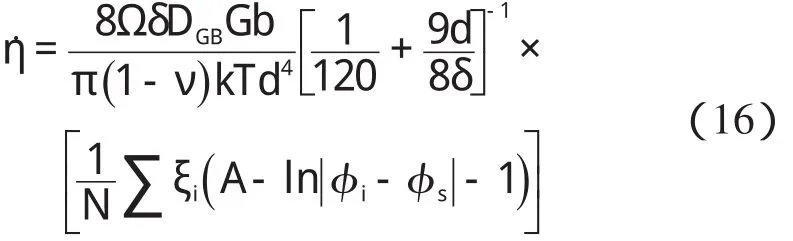
本研究把式(16)中第二个中括号内的项近似等同于一个连续的二阶导数,则式(16)可进一步简化为:

其中:

式中:Sˉmax—结构单元内晶粒的平均最大Schmid 因子值。
式(18)可以被看做是基于晶界扩散引起的晶粒旋转的剪切带演化机制,它与晶粒的尺寸、晶粒取向以及塑性变形的时间有关。
2 结果与讨论
2.1 晶粒取向对剪切带演化的影响
对于单晶来说,Schmid 因子S max=0.5 时屈服强度最低,即这种取向最软。对于纳米晶体材料而言,每一个晶粒都可以看作是单晶结构。但是,在纳米晶体材料中,各个晶粒之间的最大Schmid 因子值却各不相同。
本研究采用Brahme 的方法[14],以一个指数函数的形式给出了初始软化因子值与Schmid 因子(晶粒取向)之间的关系,即:

笔者以Cheng 等人进行的纳晶铜(d=62 nm)的拉伸试验为例,计算不同应变下软化因子的变化。纳晶铜材料的相关参数如表1 所示(应变率为1 ×10-4s-1)。
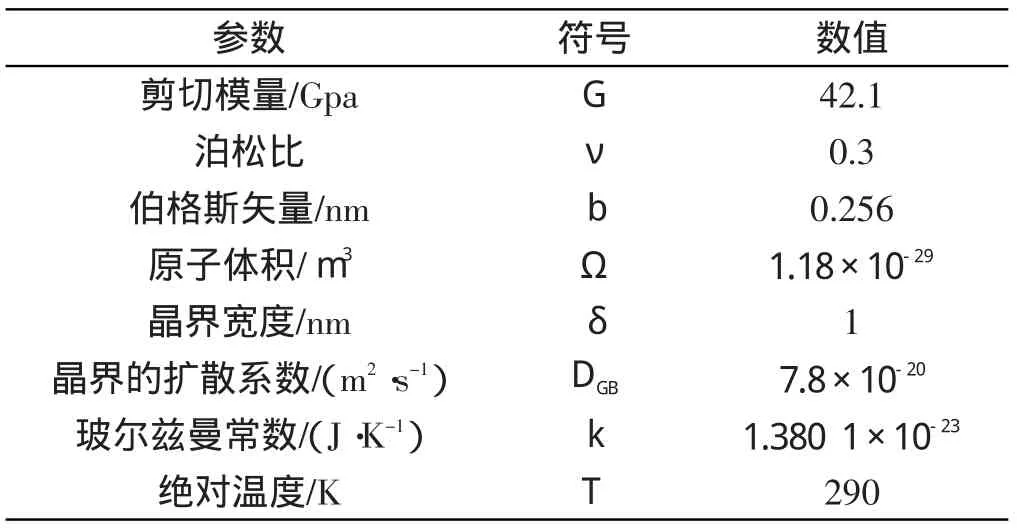
表1 纳晶铜的材料参数
本研究将图2(b)中的结构单元分成500 个晶粒集合,假定每个晶粒集合的平均最大Schmid 因子值相差0.001,根据晶粒集合的软化因子η的演化方程式(17),在不同的塑性应变值下,软化因子与平均Schmid 因子的演化如图4 所示。

图4 不同平均Schmid 因子值下,软化因子随塑性变形的演化
从图4 中可以看出,随着应变的增加,对于拥有不同的平均最大Schmid 因子值的晶粒集合,它们的软化因子值普遍有所增加。
2.2 晶粒尺寸对剪切带演化的影响
通常来说,纳米晶体材料的力学性能与晶粒尺寸有关。最近,Ramesh 等人研究了晶粒尺寸与剪切带演化的影响,但他们只考虑单一剪切带的演化,并没有考虑剪切带在纵向以及整个样本空间内总的剪切带体积的变化。
本研究中,笔者提出了基于晶粒旋转的剪切带演化机制,通过均匀化表述整个样本空间内晶粒的旋转,将剪切带的演化推广到整个空间内,从空间上研究剪切带的总的体积分数的演化。在本研究的模型中,通过晶粒尺寸对晶粒旋转的影响,考虑晶粒尺寸对剪切带演化的影响。
从公式(17)可以看出,晶粒尺寸的影响主要来自本研究给定的与扩散有关的系数ℜ。以纳晶铜为例(相关参数如表1 所示),本研究分别考虑了3 个晶粒尺寸:60 nm、100 nm 和200 nm,应变率为1 ×10-3s-1,所有样本给定相同的初始最大平均施密特因子值Sˉmax=0.3。3 种尺寸对应的剪切带体积分数的演化如图5 所示。
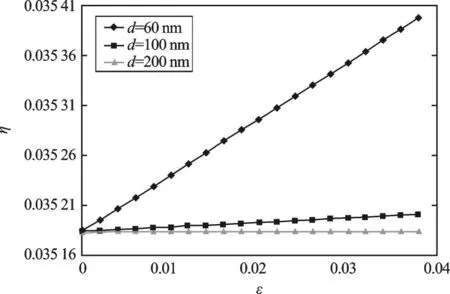
图5 不同晶粒尺寸下剪切带体积分数的演化
从图5 中可以看出,在相同的应变下,晶粒尺寸越大,剪切带的体积分数越小,这与剪切带的实验研究结果相吻合。这主要是因为:在给定的应变率下,用来表述剪切带演化的软化因子η与ℜ成正比,而ℜ与晶粒尺寸成反比关系,因此,软化因子与晶粒尺寸也成反比关系。
3 结束语
基于剪切带的特点以及晶粒旋转的表述,本研究按照晶粒取向与剪切方向的差异,将晶粒分成剪切带内容易发生滑移的软晶粒和剪切带外只发生扩散蠕变的硬晶粒,并根据扩散驱动的晶界滑移引起的晶粒旋转理论构建了一个描述剪切带演化的模型。在这一模型中,本研究同时考虑了晶粒尺寸和晶粒取向分布对剪切带演化所带来的影响。
研究结果表明:在相同的晶粒尺寸下,随着应变的增加,对于拥有不同的最大平均Schmid 因子值的晶粒集合,剪切带的体积分数普遍有所增加;在相同的应变和初始最大平均Schmid 因子值下,晶粒尺寸越大,剪切带的体积分数越小。
(References):
[1]MEYERS M A,MISHRA A,BENSON D J.Mechanical properties of nanocrystalline materials[J].Progress M ate⁃rials Science,2006,51(4):427-556.
[2]DAOM,LU L,ASARO R J,etal.Toward a quantitative un⁃derstanding of mechanical behavior of nanocrystalline met⁃als[J].Acta Mater,2007,55(12):4041-4065.
[3]JIA D,RAMESH K T,MA E.Effects of nanocrystalline and ultrafine grain sizes on constitutive behavior and shear bands in iron[J].Acta M ater,2003,51(12):495-3509.
[4]WEI Q,RAMESH K T,MA E,etal.Plastic flow local⁃ization in bulk tungsten with ultrafine microstructure[J].App lied Physics Letters,2005,86(10):101907-1-101907-3.
[5]CHENG S,MA E,WANG Y M,etal.Tensile properties of in situ consolidated nanocrystalline Cu[J].ActaM ater,2005,53(5):1521-1533.
[6]朱荣涛,周剑秋,霍如肖.粗晶与纳晶镍片拉伸力学行为[J].稀有金属材料与工程,2011,40(3):470-472.
[7]刘龙飞,胡 静,蔡志鹏,等.影响金属玻璃中剪切带行为的微观机制[J].固体力学学报,2012,33(1):69-74.
[8]JOSHI S P,RAMESH K T.Rotational diffusion and grain size dependent shear instability in nanostructured materials[J].Acta M ater,2008,56(2):282-291.
[9]HARRIS K E,SINGH V V,KING A H.Grain rotation in thin films of gold[J].Physical Review,1998,46(8):2623-2633.
[10]RAJR,ASHBY M F.On grain boundary sliding and diffu⁃sional creep[J].M etall Trans,1971(2):1113-1127.
[11]MOLDOVAN D,WOLF D,PHILLPOT SR.Theory of diffu⁃sion accommodated grain rotation in columnar polycryatal⁃line microstructures[J].Acta M ater,2001,49(17):3521-3532.
[12]READ W T,SHOCKLEY W.Dislocation Models of Crystal Grain Boundaries[J].Physical Review,1950,78(3):275-289.
[13]KIM H S,ESTRIN Y.Phasemixturemodeling of the strain rate dependentmechanical behavior of nanostructured mate⁃rials[J].Acta M ater,2005,53(3):765-772.
[14]BRAHME A,ALVIM H,SAYLOR D,etal.3D reconstruc⁃tion ofmicrostructure in a commercial purity aluminum[J].Scripta M ater,2006,55(1):75-80.

