橡胶减振元件加速寿命试验的仿真研究*

王伯平，翟敬宇，李雅淑，韩清凯

（1.空军航空大学 航空理论系，吉林 长春 130022；

2.东北大学 机械工程与自动化学院，辽宁 沈阳 110819；3.大连理工大学 机械工程学院，辽宁 大连 116024）

0 引 言

加速寿命试验属于统计试验范畴，它是在进行合理工程及统计假设的基础上，利用与物理失效规律相关的统计模型对在超出正常应力水平的加速环境下获得的可靠性信息进行转换，得到产品在额定应力水平下可靠性特征可复现的数值估计的一种试验方法。简言之，加速寿命试验是在保持失效机理不变的条件下，通过加大试验应力来缩短试验周期的一种寿命试验方法。该方法可以缩短试验时间，提高试验效率，降低试验成本[1-2]。

最早的机械结构零部件的可靠性、耐久性或者疲劳试验都是在试验场完成的，研究者通过机器的实际运转来估计零部件的可靠性指标。随着产品生产周期的不断缩短，加速试验已得到越来越多生产厂商的重视，其主要原因有两个：①加速试验可以明显缩短试验时间，降低试验成本，减少试验过程中的人力和物力消耗；②加速试验的许多试验因素都是可控的，可以得到很好的试验效果[3-6]。常用的加速寿命试验方法有恒定应力、序进应力和步进应力3 种[7-8]。

本研究选择某橡胶减振元件进行其加速寿命试验的仿真分析，首先建立其三维及有限元模型，然后通过对橡胶减振元件进行模态和瞬态分析，利用计算机仿真模拟加速试验过程。通过施加3 种不同的位移载荷，获取破坏周期，对比分析3 组试验数据，研究不同加载条件对其疲劳寿命的影响，并比较加速效果。

1 橡胶减振元件的有限元分析模型

橡胶减振元件作为主要的承力零件，容易发生破坏，并且对于橡胶制品来说，疲劳寿命一般高达106～108次，想要获得完整的试验数据，需要非常长的时间，因此笔者研究了橡胶减振元件的加速寿命试验问题。

本研究采用CATIA 软件建立了三维模型，该橡胶减振元件三维模型如图1 所示。

图1 橡胶减振元件三维模型

将三维实体模型导入ABAQUS 后，考虑整体网格划分质量及以往的经验，本研究选用C3D8H 单元模拟橡胶部分，C3D8R 单元模拟金属部分来建立有限元网格模型，该橡胶减振元件有限元模型如图2 所示，共划分了1 439 个单元。

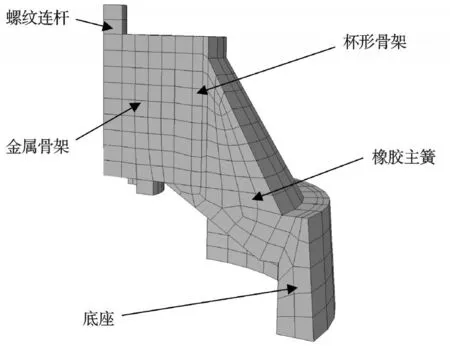
图2 橡胶减振元件有限元模型

本研究对减振元件的各部分赋予不同的材料，其特性参数如表1 所示。

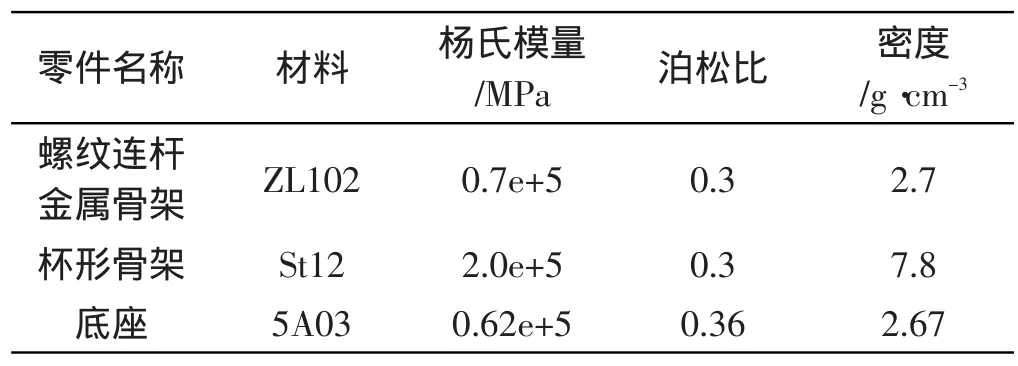
表1 橡胶减振元件各部分材料及其参数

对橡胶减振元件进行分析时，笔者将橡胶材料视为超弹性材料。超弹性材料的工程应力-应变本构关系由应变能势函数对应变不变量的导数来表达。描述橡胶类材料的力学性能的应变能势函数形式有许多种，这里采用二参数的Mooney-Rivilin 模型，即：

式中：U—应变能密度；C10，C01—Rivilin 系数，均为正定常数；I1，I2—第1、2 阶应变不变量。

二参数的Mooney-Rivilin 模型假定应变能密度是主应变常量的一次项函数，可以较好地描述橡胶类不可压缩超弹性材料在大变形下的力学特性，该模型对150%以下的应变具有很好的拟合能力[9-10]。

在采用有限元软件进行仿真计算时，研究者只需确定C10和C01 两个Rivilin 系数。常用的确定方法有经验公式、实验测试等几种。在本研究中，采用文献[11]中提供的橡胶材料本构关系力学试验数据，由ABAQUS软件应用最小二乘拟合，获得C10=0.175 529 415，C01=4.367 353 597E-3。

2 橡胶减振元件的模态分析

试验台的振动速度有一定的限制要求。它主要与由试验台、试验卡具、机械零部件等组成的试验系统动力学参数有关，特别是与试验系统的一阶固有频率关系密切。

由于加速实验台的固有频率相当高，本研究只考虑橡胶减振元件的模态。限于条件，笔者无法采用试验方法确定橡胶减振元件的固有频率。由于橡胶减振元件工作时承受的激振频率在26.7 Hz～166.7 Hz 之间，或者小于10 Hz，而在橡胶减振元件设计的过程中必然会避开易引起共振的频率范围，故其固有频率范围必定在10 Hz～26.7 Hz 之间，或者大于166.7 Hz。

因此，振动台的振动速度提升到10 Hz 也不会引起整个实验系统的共振。而常规的耐久性振动试验的试验频率为1 Hz，从模态分析的角度来看，加速试验的速度有很大的提升空间。

为了避免整个试验系统与动载荷p()t 之间不必要的动力学匹配，疲劳试验的速度极限 ft应该控制在整个实验系统的一阶固有频率的1/2 以下，即：

式中：ft—系统加载频率（cycles/s）上限，fn1—系统的一阶固有频率。

本研究中，ft取的最大值为5 Hz。

3 橡胶减振元件的瞬态分析

在分析复杂的非线性问题时，若施加位移载荷，就不必通过反复迭代来找到每个时间增量步上的位移解，使得收敛的难度大大降低。因此，本研究对橡胶减振元件上表面施加随时间变化的位移载荷。

将位移载荷分为3 组，第1 组加载过程两个阶段的幅值分别为25mm 和12.5mm，位移载荷如图3 所示。

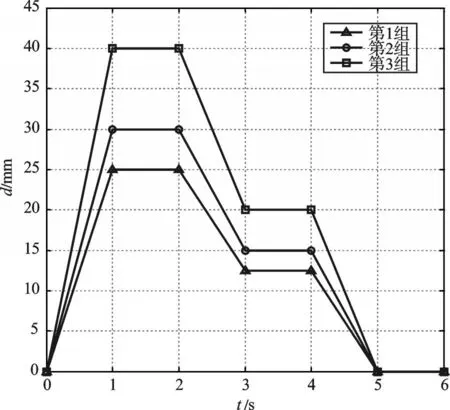
图3 位移载荷

本研究进行了应力分析，并得到橡胶减振元件的平均应力分布如图4 所示。从图4 中可以看出，橡胶主簧的根部应力最大，易于发生疲劳破坏。

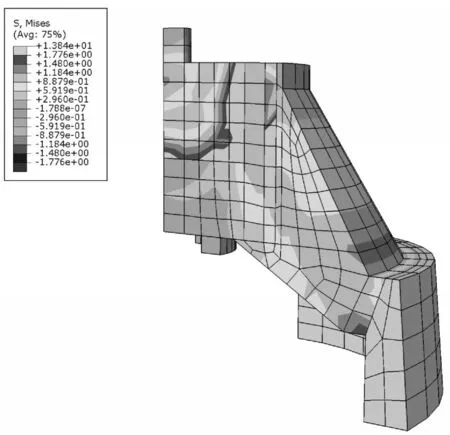
图4 橡胶减振元件的应力分布

提取橡胶减振元件危险部位的应变-时间历程曲线，如图5 所示（第1 组）。从图5 中可知，峰值点处的应变为0.421 62，仿真持续的时间为6 s。

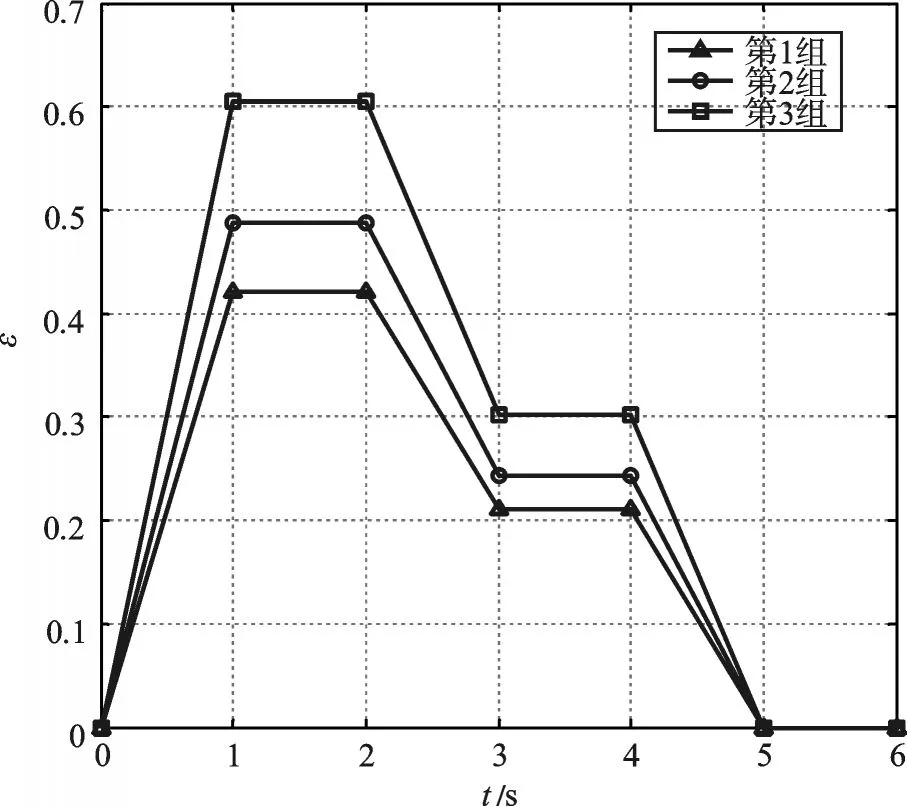
图5 危险部位应变-时间历程

本研究提升随时间变化的位移载荷的幅值，即，第2 组阶段幅值为（30 mm，15 mm），第3 组阶段幅值为（40 mm，20 mm）。位移载荷如图3 所示。3 组加载方式相同，只是幅值不同，因此橡胶减振元件的危险部位不变。提取危险部位在这两种加载条件下的应变-时间历程，如图5 所示。从图5 中可以看出，第1 组和第2组峰值点处的应变分别为0.487 526 和0.605 343。

4 寿命估计

橡胶的疲劳寿命Nf可用Manson-Coffin 关系来表述，即：

式中：n，C—与环境有关的材料常数。

该式是适用于分析橡胶材料疲劳寿命的经验公式之一。

在空气中，n 取4.6，某种橡胶材料的真实应变幅-疲劳寿命曲线如图6 所示。由上文计算出的3 组不同加载方式下峰值点处的应变值，可从图6 中得出对应的振动周期。

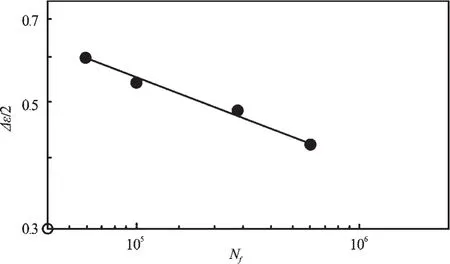
图6 某种橡胶材料在空气中的应变幅-疲劳寿命关系曲线

当本研究对橡胶减振元件加载阶段幅值为（25 mm，12.5 mm）的位移载荷时，计算得到疲劳试验需要590 000 个循环。在同样的累积损伤、疲劳破坏模型的条件下，提高加载的等级，疲劳试验的周期数就相应地缩短。

其他两组计算结果如表2 所示。

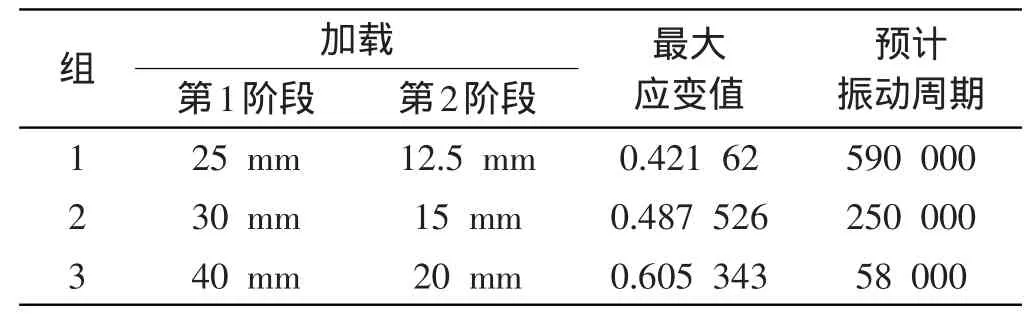
表2 等效疲劳试验数据

从表2 中可以看出，第1 组加载（阶段幅值分别为25 mm 和12.5 mm，所需实验周期为590 000）可以被第2 组（阶段幅值分别为30mm 和15mm，所需实验周期为250 000）或第3 组加载（阶段幅值分别为40 mm和20mm，所需实验周期为58 000）所取代。

这些不同的加载在理论上可以导致相同的疲劳破坏。但是，有一点需要指出的是，在改变加载的同时，疲劳破坏的变化也需要注意。这是因为，加载的周期数较多时，零部件的损伤是弹性的，当过大地提高加载级别、缩短加载周期数时，损伤的形式可能会变成塑性的。

5 结束语

本研究对发动机橡胶减振元件的的加速寿命试验问题进行了仿真研究。

首先，本研究在建立了橡胶减振元件三维实体及有限元网格模型的基础上，分析得出其一阶固有频率范围为10 Hz～26.5 Hz，由动力学匹配关系确定了加速寿命试验系统的极限频率为5 Hz。

然后，对上述模型进行了瞬态动力学分析。对模型施加3 组不同幅值的位移载荷（（25mm，12.5mm）、（30 mm，15 mm）、（40 mm，20 mm）），获得了3 组不同加载方式下峰值点处的应变值分别为0.421 62、0.487 526、0.605 343。

最后，由橡胶材料的应变幅-疲劳寿命关系曲线，获得了3 种加载条件下的预计振动周期为5.9 ×105、2.5 ×105、2.5 ×104。第2 种加载方式获得的破坏周期比第1 种缩短了3 倍，第3 种比第1 种缩短了近12 倍。仿真试验结果表明，试验的加速效果明显，试验周期大大减小。

（References）：

[1]王霄锋，管迪华.汽车零部件耐久性试验方法研究[J].汽车工程，1992，14（4）：224-229.

[2]王霄锋.汽车可靠性工程基础[M].北京：清华大学出版社，2007.

[3]KLYATISLM.The Strategy of Accelerated Reliability Test⁃ing Development for Car Components[N].SAE Paper，2000-01-1195.

[4]KLYATIS L M，KLYATIS E.Accelerated Reliability Test⁃ing Problems Solving[N].SAE Paper，2004-01-1139.

[5]LEDESMA R，JENAWAY L，WANG Y.Development of Ac⁃celerated Durability tests for Commercial Vehicle Suspen⁃sion Components[N].SAE Paper，2005-01-3565.

[6]RISAM G S，BALAKRISHNAN S，PATIL M G.Methodolo⁃gy for Accelerated Vibration Durability Test on Electrody⁃namic Shaker[N].SAE Paper，2006-32-0081.

[7]潘 骏，刘红杰，陈文华，等.航天电连接器步进应力加速寿命试验研究[J].机电工程，2011，28（2）：172-183.

[8]陈文华，刘俊俊，潘 骏，等.步进应力加速寿命试验方案优化设计理论与方法[J].机械工程学报，2009，46（10）：182-187.

[9]才建军.汽车发动机液压悬置的动特性仿真与试验研究[D].沈阳：东北大学机械工程与自动化学院，2007.

[10]洪欢欢，吴茂敏，陈 建，等.基于油锯减振的转换桥方法研究[J].轻工机械，2011，29（4）：11-16.

[11]祖景平，钱英莉，周华樟.ABAQUS6.6 基础教程与实例详解[M].北京：中国水利水电出版社，2008.