液压挖掘机标准负载工况的研究*
于洪光,高 峰*,柳桂国,杨庆华
(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310014;2.浙江工商职业技术学院,浙江 宁波 315012)
0 引 言
对于室内加载试验,负载的模拟一直是实验的重点与难点,模拟的准确与否直接影响到试验结果的准确性。目前,我国还未出台有关挖掘机负载工况的相关标准,大部分挖掘机研发试验还是以特定的现场作业为准[1-2]。但标准工况在相关领域已有研究,如城市道路有美国的FTP-75工况、欧洲的ECE-15工况等,在汽车研发的道路模拟实验中发挥了重要的作用。一般说来,合成工况的方法有两种:一种是取自实测记录,如美国的FTP-75工况;另一种是由实测数据强制合成,如欧洲的ECE-15工况[3]。
Kruse and Huls最先提出了一种数据合成的方法。该方法以工作循环周期内包含的工况数为准则数,从实测数据中节选一定数量的工作周期,在时间序列上将各种工作模式连接成标准工况。Andre等则是对速度一时间曲线进行分析,把每个行驶段看作是一系列的动力学序列,将不同类型的序列连接在一起。瑞典的Ericsson通过对大量实验数据的分析处理,从中提取出62个特征参数,应用统计方法,从中筛选出16个相互独立的特征参数,用于工况的合成。Kuhler and Karstens等则提出了基于平均速度、平均加速度、平均减速度、一个行驶段的平均距离及平均加减变化次数等10个强制性参数合成的一个行驶工况。国内的研究机构,如香港理工大学、中国环境科学研究院、天津大学等采用的方法大多与该方法类似,只是参数的选择及参数的个数略有不同[4]。
由于挖掘机工况复杂,信号突变较多,用特征参数强制合成很难复现原始波形,本研究采用Kruse and Huls的方法,以每个工作周期内包含的不同工作模式为聚类对象,最终在时域上合成完整的挖掘机负载工况,并将计算所得负载工况与样本信号的相似度进行比较,从而验证该方法的可行性。
1 信号特点分析
1.1 周期性强
液压挖掘机工作过程具有明显的周期性,一个工作循环大致包含挖掘、满斗举升回转、卸载和空斗返回等工况,因此采集到的负载也应呈现明显的周期性。
本研究对样本信号作自相关分析[5],样本信号自相关函数图像如图1所示。

图1 样本自相关函数
由图1可看出,在t稍微偏离0的时候信号大幅衰减且呈现周期性波动,根据自相关函数的性质,自相关函数具有与周期信号相同的周期性,进一步验证了挖掘机负载的周期性。
1.2 多突变
在研究道路行驶工况中,研究者常采用建立运动学特征表的办法,用一定数量的特征参数确定信号所属的运动模式,以达到对每个工作模式分别聚类的效果,最终合成行驶工况。由图1不难看出,挖掘机负载信号存在大量的突变信号,而在道路行驶工况中不存在这样的突变,因此在道路行驶工况研究中被广泛运用的平均加速时间、平均减速时间、最大加速度、最大减速度等特征值不能用来描述负载信号。其次在验证工况有效性时,道路行驶工况研究中多通过计算大量特征参数的误差来综合分析所得工况的有效性,该方法同样不适用于挖掘机负载工况。
1.3 工况结构复杂
虽然挖掘机每个工作循环中包含了特定的几个工作模式,但与道路行驶工况相比,各工作模式在负载信号中体现的并不明显,呈现的波动要远多于实际工作模式,因此分割节点的选取不应以工作模式为依据。
2 挖掘机负载工况的研究
2.1 样本长度的选取方法
从工程实际考虑,样本长度过长会造成不必要的人力、物力的浪费,过短则会使采样结果不能真实反映实际工作情况,因而确定实验样本长度是很有必要的。本研究采用近似均值估计法计算挖掘机负载样本长度,为信号采集及验证负载工况的有效性提供依据[6]。
2.2 负载工况制定
(1)本研究通过EMD自适应滤波获取单工作周期子样本序列[7],其流程图如图2所示。
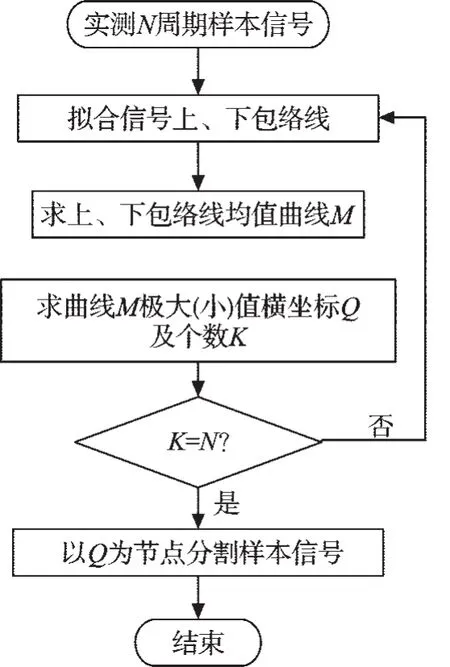
图2 获取单工作周期子样本序列程序流程图
(2)获取单工作周期内分割节点。实测信号中每个完整的波峰可代表挖掘机的一个独立的动作,以此为依据求取节点分割信号。由于每个动作的波形中掺杂有大量小的波动,要求取的节点实际上是信号的局部最值,为排除其他极值点的干扰,本研究首先对信号做平滑处理,采用加噪边界模糊化后再拟合包络线的方法去除小的波动,最终保留与挖掘机实际工作相对应的主要波动。最后采用求极值点的办法将信号分割,获取对应不同动作的信号片段。
Matlab程序流程图如图3所示。
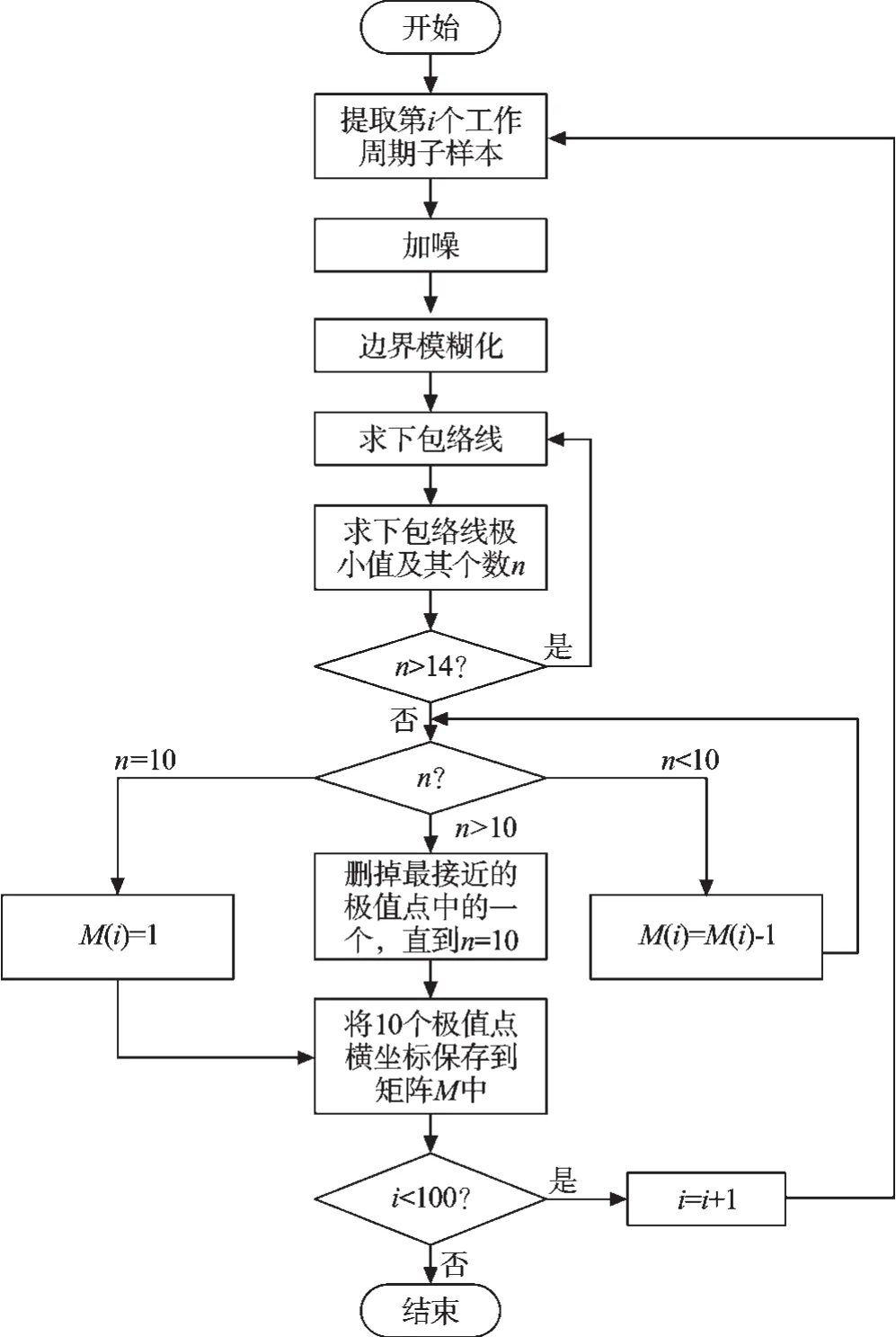
图3 获取单工作周期内分割节点程序流程图
2.3 合成工况
本研究通过上步求取分割节点后将每个周期的样本信号分割成9个主要的运动片段,在时序上这9个片段是一一对应的,将每个片段分别做统计处理,为完整复现信号的突变特性同时不被个别不稳定噪声干扰,采用对所提取的单个动作的样本信号作求同处理的方法,从而最大限度地保留了信号的主要成分,删掉了个别噪声,而且保留了各动作在整个循环工况中的比例,最后将统计结果合成为标准工况。
2.4 相关性分析
皮尔森相关系数也称皮尔森积矩相关系数,是一种线性相关系数。皮尔森相关系数是用来反映两个变量线性相关程度的统计量。相关系数用r表示,其中n为样本量,即:

式中:x—实测样本数据,y—负载标准工况,r—两个变量间线性相关强弱的程度。
r的取值在-1与+1之间,若r>0,表明两个变量是正相关,即一个变量的值越大,另一个变量的值也会越大;若r<0,表明两个变量是负相关,即一个变量的值越大另一个变量的值反而会越小。r的绝对值越大表明相关性越强。
3 实验结果与分析
3.1 样本长度计算
本研究按大约5个工作循环为一个子样本,可求得采集的20个子样序列的均值,分别求出均值序列的标准差S()xˉ和均值。根据相对统计误差的定义可计算相对统计误差:

本研究根据计算结果给定统计误差εr为2%。以作为相对误差,置信度为68.3%,且:
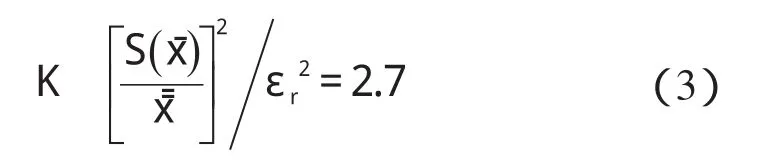
取K=3,可得样本长度为3×5=15斗。以作为相对误差,置信度为95.4%,且:
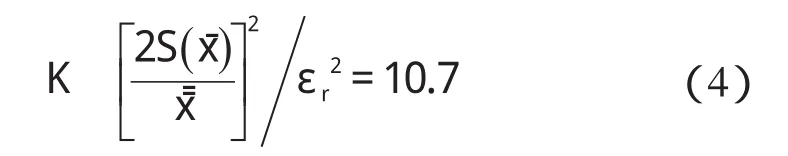
取K=11,可得到样本长度为11×5=55斗[8]。
3.2 合成工况
(1)EMD自适应滤波获取单工作周期子样本序列,获取分割节点如图4所示。
(2)运动片段分割。
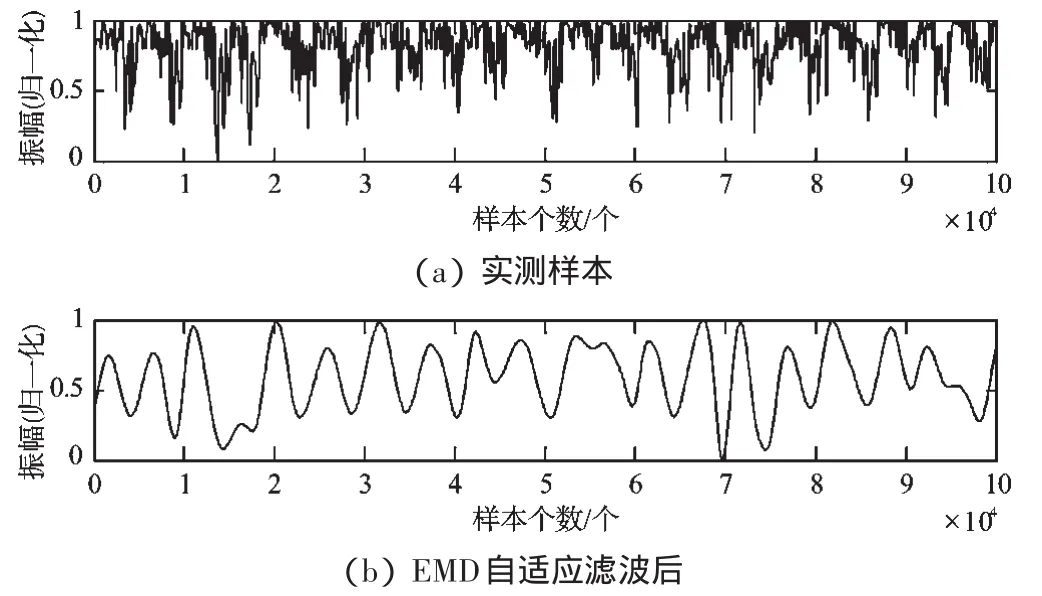
图4 EMD自适应滤波获取周期节点
某工作周期内分割节点提取过程及效果如图5所示:
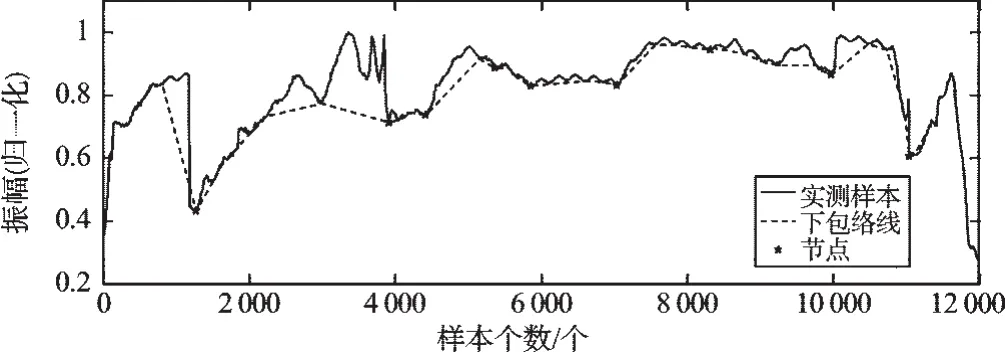
图5 某工作周期内分割节点的提取
(3)合成工况与样本信号对照。
样本信号与本研究方法得出的标准负载工况对照图如图6所示。
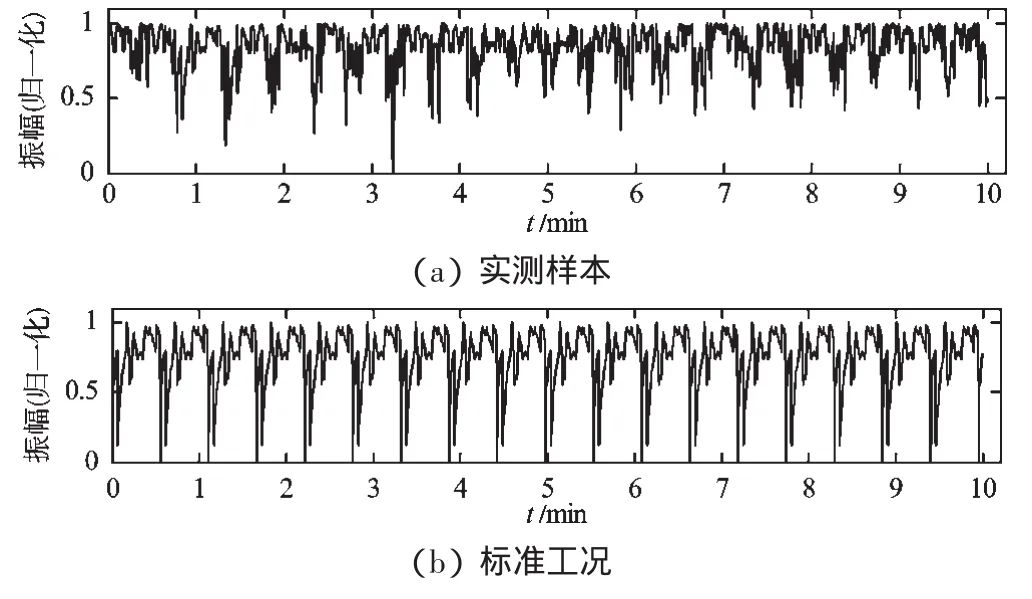
图6 样本与标准工况约20个工作周期的对照图
3.3 相似度分析
(1)线性相关性。本研究通过计算标准负载工况与实测样本信号的皮尔森相关系数,以验证两者的线性相关性,从而可以验证该方法得到的标准工况与实测样本信号的相似度。式(1)中,样本量n为390 274,经计算,得标准工况与原始信号的皮尔森相关系数为0.957 1,具有较高的线性相关性。
(2)统计特性对比[9]。统计特性对照表如表1所示。由表1可以看出,实测样本与标准工况在统计特性上具有较高的一致性。
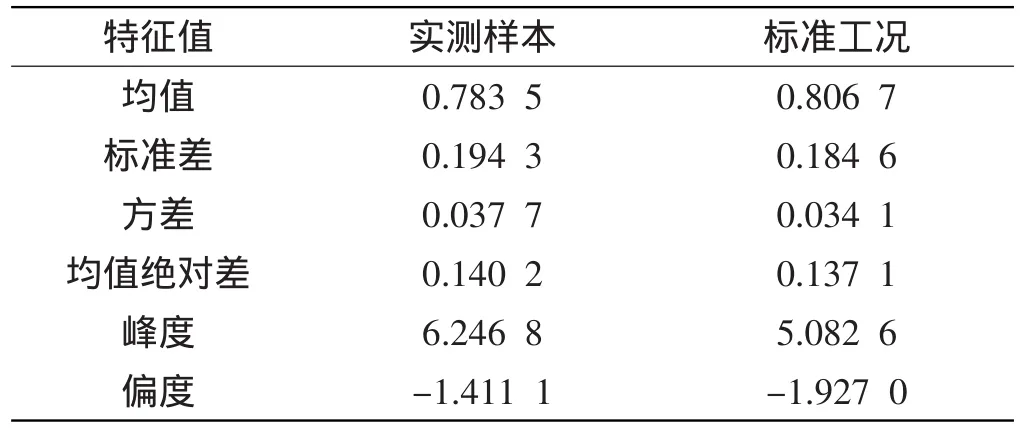
表1 统计特性对照表
3.4 局限性
该工况合成的方法首先要求信号要有稳定的周期性,因此对不具有周期性的负载工况不适用。
4 结束语
(1)本研究采用近似均值估计法计算得到挖掘机负载信号最低采样长度为55斗,为挖掘机负载工况制定提供了合理有效的样本长度。
(2)基于Kruse and Huls提出的工况合成的方法,本研究结合挖掘机实际工作模式,通过有效次数求信号包络线的方法求取分割节点,对不同工作模式作统计分析,最终在时域上合成完整的负载工况,通过计算标准工况与实测样本信号的皮尔森相关系数以及主要的统计特征值。研究结果表明,该方法合成的标准负载工况与实测样本具有较高的相似度。
(References):
[1] 邸鹏远,史文辉,李 隽,等.液压挖掘机能耗试验与评价方法[R].国家工程机械质量监督检验中心,2009.
[2] 高 峰.液压挖掘机节能控制技术的研究[D].杭州:浙江大学机械工程学系,2001:10-14.
[3] ANDRE M,HICKMAN A J,HASSEL D,et al.Driving Cy⁃cles for Emission Measurements under EuropeanConditions[N].SAE Papers,950926,1995.
[4] 姚志良.北京市汽车行驶工况和汽车排放特性的研究[D].北京:北京工商大学化学与环境工程学院,2004:1-23.
[5] 黄娇英.基于EMD和自相关分析的轮胎音频信号处理[J].电子测量与仪器学报,2009(9):37-41.
[6] 张云龙.装载机传动系载荷样本长度的确定[J].工程机械,1994,25(6):16-18.
[7] SUJAN K R.MOLLA M K I.Harmonic modification and data adaptive filtering based approach to robust pitch esti⁃mation[J].International Journal of Speech Technology,2011,14(4):339-349.
[8] VAHEDI E,ZEIN E L,PRICE W W.Dynamic load model⁃ing in large scale stability studies[J].IEEE Transactions on Power Systems,1988,3(3):1039-1045.
[9] 苏金明,阮沈勇.MATLAB6.1实用指南[M].北京:电子工业出版社,2002.

