动力学模型在荧光定量PCR数据处理中的优势

刘彦礼 李旭 苏振成 徐明恺 张惠文

自1993年第一次出现有关荧光定量PCR技术的记录，1996年ABI（Applied Biosystems）公司使荧光定量PCR（real-time fluomgenetic quantitative PCR，FQ-PCR）技术商业化，并制造出第一台荧光定量PCR仪，迄今因该技术较以往核酸定量研究方法，如Nothern blotting、RNase-protection、Semiquantitative RT-PCR等，具有灵敏度高、特异性和可靠性好、自动化程度高、具实时性和准确性等特点，所以目前广泛应用于分子生物学研究和医学研究等领域［1-4］。实时荧光定量PCR是在PCR定性技术基础上发展起来的核酸定量技术。它是通过在PCR反应体系中加入荧光基团（探针类和染料类），利用每个循环末对荧光信号积累的捕捉来实时监测整个PCR进程，从而建立起荧光量与初始模板量的对应关系，最后通过标准曲线对未知模板进行定量分析的方法［5］。对于荧光定量PCR数据分析方法包括绝对定量和相对定量两种。前者是应用精确定量的标准品，构建标准曲线，以此来定量未知样品中初始基因拷贝数。虽然该方法能够直接得到目的基因的拷贝数，且具有稳定、直观等优点，但是其数据可靠的前提是得到精确定量的标准品，鉴于目前核酸定量技术的不足，标准品的制备无统一标准，所以数据缺乏可比性；而且标准品与试验样品扩增效率的差异也影响了该方法应用；再者绝对定量也不适合高通量的定量分析。而相对定量在一定程度上弥补了绝对定量的不足，其是指在测定目的基因的同时测定一内源性稳定表达内参基因，通过比较处理前后的目的基因相对于内参基因归一化的比值，来衡量目的基因在处理前后的表达差异，并不需要确定目的基因具体的拷贝数。尽管相对定量存在着一定的缺点，但其仍是目前处理荧光定量数据的主流方法，尤其是定量mRNA拷贝数［6］。本试验在用上述3种方法就行处理数据的过程中，假定未稀释样品为对照（control），不同的稀释梯度的样品为处理（sample），理论上目的基因IL-10的变化率为1。最终通过比较不同方法计算的结果与理论值的差异进行分析，旨在探讨动力学模型在定量结果的可靠性、方便性及经费节约方面的应用前景。

1 材料与方法

1.1 材料

1.1.1 主要试剂和仪器 Taq DNA 聚合酶、SYBR Premix Ex TaqTMⅡ（Perfect Real Time）购自大连宝生物工程有限公司；ABI 7000型实时荧光定量 PCR扩增仪为美国ABI公司生产；Univeral Hood SN-75S型紫外凝胶成像系统为美国Bio-Rad公司生产。

1.1.2 试验样品 本试验所应用的内参基因（β-actin）与目的基因（IL-10）的cDNA由本课题组通过反转录得到，并对得到的cDNA进行5倍的梯度稀释。

1.2 方法

1.2.1 荧光定量PCR反应条件确定 利用体外转录生成的 cDNA 作为模板，从多次重复性试验中发现，该检测方法最适反应总体积25μL，其中模板1μL；最适的引物浓度为0.4μmol/L，其余组分浓度依据试剂盒使用说明。最适循环参数为：95℃ 30；之后 95℃ 5s，60℃ 30s，72℃ 31s，40 个循环 ；最终72℃ 5min。PCR反应完成后以60℃为起点做产物的熔解曲线。β-actin特异性引物（F：5'-TGGAATCCTGTGGCATCCATGAAAC-3'，R：5'-TAAAACGCAGCTCAGTAACAGTCCG-3'）与IL-10的特异性引物（F：5'-ACCTGGTAGAAGTGATGCCCCAGGCA-3'，R ：5'-CTATGCAGTTGATGAAGATGTCAAA-3'），扩增片段大小分别为348bp和237bp［7］，由华大基因合成。

1.2.2 相对定量方法

1.2.2.12－△△Ct法 该方法是传统的处理荧光定量数据的方法，其通过假设目标基因与内参基因扩增效率相等且均为100％，即Etarget=Eref= 1［8］，这样大大简化了试验数据的处理过程，其数学模型基于PCR指数扩增的公式：

Xn= X0×（1+ E）n

其中Xn是循环数为n时基因的拷贝数，X0为初始基因拷贝数，E为基因的扩增效率，Ct代表目标扩增产物达到设定阈值所经历的循环数，因此

XCt-target= X0-target×（1+ Etarget）Ct-target=Ktarget

其中XCt-target为目标基因达到设定阈值时的拷贝数，X0-target为目标基因初始拷贝数，Ct-target为目标基因扩增到设定阈值时的循环数，对于目标基因和内参基因来说，达到阈值时其基因拷贝数固定，所以Ktarget为常数，同理：

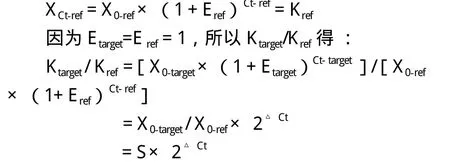
其中X0-target/X0-ref代表经过内参基因归一化处理的初始目标基因拷贝数的比值，用S表示；△Ct表示目标基因和内参基因Ct值的差异，△Ct = Cttarget － Ct-ref；Ktarget/Kref为一常数，设为K，对公式进行变形得：

S = K × 2－△Ct

因此用处理后样品的Ssample除以处理前样品的Scontrol得到：

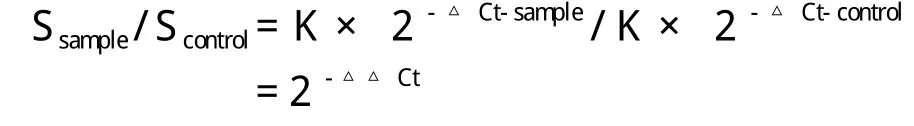
公式中的－△△Ct = △Ctsample－△Ctcontrol

1.2.2.2 双标准曲线法 该方法应用上述准备好的梯度稀释cDNA分别做出目的基因与管家基因的标准曲线，然后从各自的标准曲线上求出初始模板量，经管家基因归一化处理后，求出目的基因的相对含量［9，10］。其也基于PCR指数扩增的公式：

Xn= X0×（1 + E）n

其中Xn是循环数为n时基因的拷贝数，X0为初始基因拷贝数，E为基因的扩增效率，当荧光值达到阈值时其数学公式表示如下：

XCt= X0×（1 + E）Ct

两边同时取对数：log XCt= Ct×log（1 + E）+ log X0，变形得：

Ct = － log X0/log（1+E）＋ log XCt/log（1+ E）

由于达到阈值时，XCt和E为常数，所以设

a = － 1/log（1 + E）；b = log XCt/log（1 + E）

则公式转化为线性方程：

Ct = a×log X0＋ b

由此构建出基因初始拷贝数与Ct的线性关系。从而通过求出未知样本内目标基因的Ct值即可求出目标基因的相对初始拷贝数。通过上述模型，我们进行目标基因的相对定量：

由以上公式可以求出X（target-control）（处理前样品中目标基因的相对初始拷贝数）、X（ref-control）、X（target-sample）和X（ref-sample），归一化处理表示目的基因在处理前后的表达差异率Ratio为：

Ratio =［X（target-sample）/X（ref-sample）］/［X（target-control）/X（ref-control）］

将 a = － 1 /log（1 + E）；b = log XCt/log（1 + E）带入公式后，整理得：

Ratio =（1+Etarget）△Ct（control-sample）/（1+Eref）△Ct（control-sample）

若假设上述公式Etarget=Eref= 1，则ratio =2－△△Ct，其中－△△ Ct = △ Cttarget－△ Ctref，因此可以将2－△△Ct法作为双标准曲线法的一个特例。

1.2.2.3 基于动力学的相对定量方法 通过上述两种计算方法的比较，可以明确基因的扩增效率对后期数据处理的影响，并且这种影响通过指数形式进行放大。上述两种计算方法假定PCR反应在指数扩增期时效率相等，但实际情况却是在制备样品cDNA的过程中，已经将不同浓度的盐、酚、氯仿、乙醇等带入到样品中，这些有毒物质将不同程度的抑制酶的活性，使实际的扩增效率低于理想值；并且在样品的梯度稀释过程中，这些有毒物质也被稀释，

因此减少了对酶的抑制，这就造成了梯度稀释样品本身的扩增效率就不一致，从而使通过双标准曲线法得到的值与真实值有差异［11］。针对这种情况，近年来许多文献［12-16］提出通过模拟荧光定量PCR仪所给出的样品扩增曲线建立荧光量与Ct值之间的直线或曲线，以此来获得反应的扩增效率或基因初始拷贝数，并且设计出一系列方便试验人员进行试验的模型和软件。该模型假定在单一PCR扩增反应的指数期内期扩增效率恒定，建立荧光量的对数值与Ct值之间的线性关系，从而获得反应扩增效率，经管家基因归一化处理后得到目的基因在处理前后的表达差异。其模型与双标准曲线法相似，但不是通过对样品梯度稀释获得标准曲线间接获得扩增效率，而是利用每个梯度样品的真实扩增曲线来获得我们需要的荧光量和与之对应的Ct值，从而直接得出该梯度PCR反应的扩增效率。Ramakers等［8］在此基础上设计出软件LinRegPCR以为广大研究者提供方便。由假设可知：

Fn= F0×（1 + E）n

其中Fn是循环数为n时基因扩增产物的荧光量，F0为初始基因的荧光量，E为基因的扩增效率。当荧光值达到阈值时数学公式表示如下：

FCt= F0×（1 + E）Ct

两边同时取对数：log FCt= Ct×log（1 + E）+log F0变形得：Ct = log FCt/log（1 + E）－log F0/log（1 + E）

因为是单一反应模板量恒定，所以log F0为一常数，且E值恒定。

若设 a = 1/log（1 + E）；b = log F0/log（1 + E），则公式简化为：

Ct = a × log FCt－ b

当在扩增的指数期，通过取一系列的荧光值以及与之对应的Ct值，线性拟合求出E值后，带入公式：Ratio =（1+Etarget）△ Ct（control-sample）/（1+Eref）△ Ct（control-sample）

通过Ratio值反应出目的基因在处理前后的表达差异。

2 结果

2.1 荧光定量PCR操作特异性与重复性检验

试验通过荧光定量PCR给出的熔解链曲线（图1），并辅助以琼脂糖凝胶电泳验证该方法的特异性（图2），从图1中熔解链曲线只有单一的峰以及图2中琼脂糖凝胶电泳跑出的单一条带，这些都很好的说明了所采用引物的高特异性；同时通过对同一样品在3个时间点，每个时间点上做3个重复以验证方法的可重复性和稳定性，通过特异性和重复性检验很好地保障了试验数据的可靠性。

图1 β-actin和IL-10熔解链曲线

图2 荧光定量PCR仪扩增结果

2.2 梯度稀释样品荧光定量结果

对于样品cDNA进行5倍梯度稀释后，每个梯度3个重复，测得相应β-actin和IL-10的平均Ct值如表1所示。

2.3 三种相对定量方法结果

2.3.12－△△Ct法定量结果 由表3数据通过2－△△Ct方法计算出目的基因IL-10通过内参基因β-actin归一化处理后变化率如表2所示。

2.3.2 双标准曲线法定量结果 由表3数据构建β-actin和IL-10的标准曲线（图3），利用线性拟合得到的斜率计算出Eβ-actin=0.5959，EIL-10=0.6886；通过前述公式计算出目的基因IL-10经内参基因β-actin归一化处理后变化率如表3所示。

2.3.3 基于动力学的相对定量方法结果 根据动力学相对定量方法原理，在β-actin和IL-10扩增曲线的直线部分（图4-a）随机采集5个点，获得与之对应的荧光量与Ct值，线性拟合得到相应的扩增效率（图4-b），通过相应公式得出目的基因IL-10经内参基因β-actin归一化处理后变化（表4）。

表1 荧光定量5倍梯度稀释后样品的数据

表2 2－△△Ct法定量结果

表3 双标准曲线法定量结果

3 讨论

3种模型处理数据的结果见表5。理论上同一样品梯度稀释后，其作为样品的各个梯度中目的基因经表达差异率（Ratio）和经内参基因归一化处理后相对于对照应为常数1。相同的原始数据通过3种模型处理后的定量结果与理论值比较，从均值、方差以及变异系数方面都说明动力学方法要优于双标准曲线法和2－△△Ct法。动力学方法与双标准曲线法计算出内参基因与目的基因的扩增效率均小于1，这与实际PCR过程的动力学相符，也直接说明了2-△△Ct法本身的前提条件就存在着不足，而且动力学方法所计算得到的每个梯度扩增效率随着稀释梯度的增加也随之增加，进一步证明了模板制备中存在的有毒物质在PCR反应过程中对酶活性的影响。

图3 β-actin和IL-10的标准曲线

图4 β-actin和IL-10的扩增曲线及直线部分线性拟合

表4 动力学方法定量结果

表 5 三种数学模型处理结果的比较

但因2－△△Ct法对假设的简化使得该方法只需一个变量（Ct值），即可快速获得结果；同时，目的基因表达差异率越大该方法的可靠性就越高，故现在仍被广泛使用；双标准曲线法通过构建标准曲线获得内参基因与目的基因的扩增效率，然而标准品稀释的同时也稀释了抑制PCR反应的有毒物质，使由该方法得到的扩增效率与真实值有一定误差，并且通过这种方法所构建的标准曲线消耗了更多的定量试剂，增加了试验成本，所以现在应用较少。随着荧光定量上游技术的突破，试验所得原始数据的可靠性越来越高，而动力学模型因以实时定量曲线为基础通过线性拟合计算得到每一个基因的扩增效率，所以通过模型有效的屏蔽了PCR反应过程中潜在的影响因素，计算所得扩增效率的可靠性也随之越来越高；同时因省去标准曲线来计算扩增效率，减少了试剂的消耗，降低了试验成本，节省了有限的模板；而且针对动力学模型使用过程中遇到的线性拟合的问题，已经开发出多款供研究者利用的软件，如LinRegPCR。

4 结论

在荧光定量PCR相对定量的数据处理过程中，通过实例对3种处理数据模型的精确性进行比较，发现动力学模型＞双标准曲线法＞2－△△Ct法；此外应用动力学模型在节约试验成本以及模板等方面的优势也使其成为荧光定量研究领域中的一个热点，围绕其开发的多款软件也表明该模型具有很大的发展前景。

［1］ Higuchi R, Fockler C, Dollinger G, et al.Kinetic PCR analysis-Real-timemonitoring of DNA amplification reactions.Biotechnology,1993, 11（9）：1026-1030.

［2］ Heid CA, Stevens J, Livak KJ, et al.Real time quantitative PCR.Genome Research, 1996, 6（10）：986-994.

［3］ VanGuilder HD, Vrana KE, Freeman WM.Twenty-five years of quantitative PCR for gene expression analysis.Biotechniques, 2008,44（5）：619-626.

［4］ Thellin O, ElMoualij B, Heinen E, Zorzi W.A decade of improvements in quantification of gene expression and internal standard selection.Biotechnology Advances, 2009, 27（4）：323-333.

［5］ Tevfik Dorak M（Ed.）.Real-time PCR［M］.New York：Taylor＆ Francis Group, 2006.

［6］ Valasekl MA, Repa JJ.The power of real-time PCR.Advances in Physiology Education, 2005, 29（3）：151-159.

［7］ Ulett GC, Ketheesan N, Hirst RG.Cytokine gene expression in innately susceptible BALB/cmice and relatively resistant C57BL/6mice during infection with virulent Burkholderia pseudomallei.Infect Immun, 2000, 68（4）：2034-2042.

［8］ Ramakers C, Ruijter JM, Deprez RHL, et al.Assum-ption-free analysis of quantitative real-time polymerase chain reac-tion（PCR）data.Neuroscience Letters, 2003, 339（1）：62-66.

［9］ Pfaffl MW.A newmathematicalmodel for relative quantification in real-time RT-PCR.Nucleic Acids Research, 2001, 29（9）：e45.

［10］ 张驰宇, 徐顺高, 黄新祥.一种新颖简便的荧光实时RT-PCR相对定量方法的建立.生物化学与生物物理进展, 2005, 32（9）：883-888.

［11］ Liu W, Saint DA.A new quantitativemethod of real time reverse transcription polymerase chain reaction assay based on simulation of polymerase chain reaction kinetics.Analytical Biochemistry,2002, 302（1）：52-59.

［12］ Goll R, Olsen T, Cui GL, et al.Evaluation of absolute quantitation by nonlinear regression in probe-based real-time PCR.BMC Bioinformatics, 2006, 7：107.

［13］ Rutledge RG.Sigmoidal curve-fitting redefines quantitative realtime PCR with the prospective of developing automatedhighthroughput applications.Nucleic Acids Research, 2004, 32（22）：e178.

［14］ Tichopad A, Dilger M, Schwarz G, et al.Standardized determination of real-time PCR effciency from a single reaction set-up.Nucleic Acids Research, 2003, 31（20）：e122.

［15］ Alvarez MJ, Vila-Ortiz GJ, Salibe MC, et al.Model based analysis of real-time PCR data from DNA binding dye protocols.BMC Bioinformatics, 2007, 8：85.