具有时滞和阶段结构的捕食系统的分析

崔 信

（晋中职业技术学院，山西 晋中030600）

自从Aiello和Freedman建立了具有阶段结构的种群模型［1］之后，具有阶段结构的生物模型受到众多学者的重视［2－3］。文献［4］讨论了文献［3］对应的自治系统的一致持久性及具有无限时滞的阶段结构模型的持久性；文献［5－6］讨论了食饵和捕食者都具有阶段结构的周期捕食系统的一致持久性和正周期解的存在性；文献［7］研究了食饵具有阶段结构和捕食者具有消化时滞τ的阶段结构捕食模型的全局稳定性和永久持续生存。上述文献中考虑的出生率都是关于种群密度的线性函数，而考虑非线性出生率的种群模型研究较少［8］。本文在文献［8］基础上，考虑食饵种群具有阶段结构及非线性出生率，而捕食者种群仅捕食幼年食饵。我们建立模型如下：

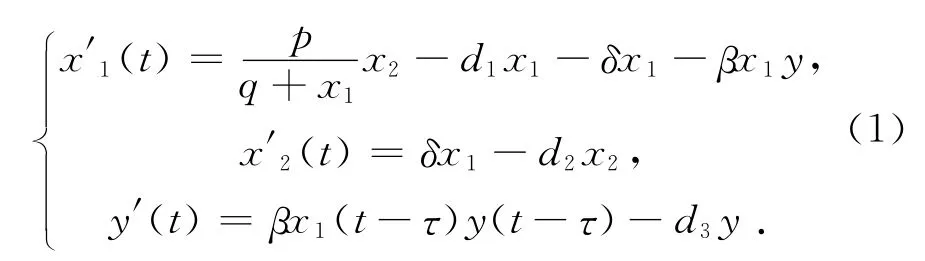
其中：x1（t），x2（t）分别是食饵种群的幼年种群和成年种群的密度函数，y（t）是捕食者种群的密度函数。模型（1）的建立基于下列基本假设：

（H1）食饵种群：幼年食饵种群具有非线性出生率p／（q＋x1），幼年体食饵的死亡率为d1，幼体向成体的转化率为δ，成体食饵的死亡率d2．

（H2）捕食者种群：假定这里捕食者只捕食幼年食饵，捕食者的生存依赖于幼年种群的生存状况。捕食者的死亡率为d3，消耗率为β，捕食者种群并不及时繁殖，而是经过一段消化时间τ之后才繁殖。参数p，q，d1，d2，d3，δ，β都是正常数。

系统（1）的初始条件为：

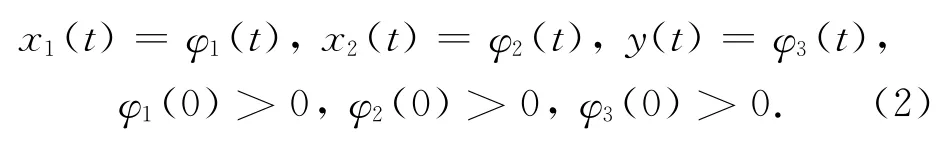
其中，φi（t）（i＝1，2，3）是［－τ，0］上的非负连续函数。

1 预备知识

易知系统（1）满足初始条件（2）的解具有正性。我们首先讨论解的有界性。

定理1 当存在常数M1＞0，M2＞0，使得系统（1）－（2）的任一解 （x1（t），x2（t），x3（t）），当t充分大时，满足x1（t）＜M1，x2（t）＜M1，y（t）＜M2。

证明 首先考察系统（1）缺少捕食者种群的子系统

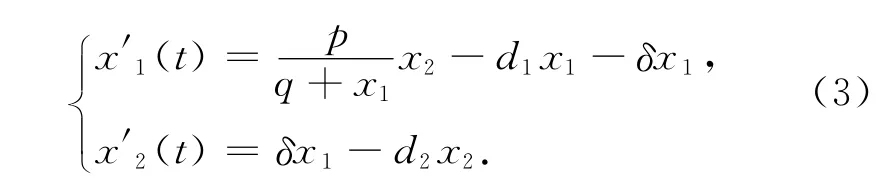
这里系统满足初始条件x1（0）＞0，x2（0）＞0．

记V（t）＝x1＋x2．把方程（3）两边同时相加可得：

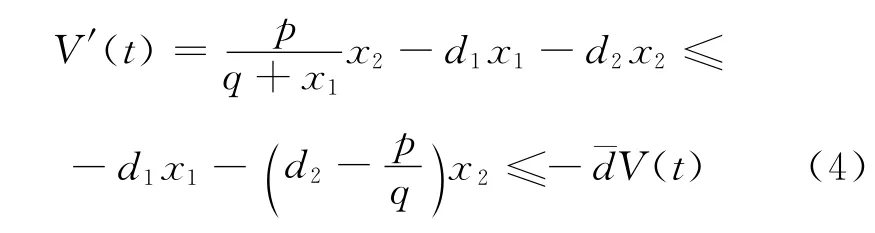
从（4）式易知，存在M1＞0，对所有的t＞0有0＜V（t）＜M1．由解的正性可知0＜x1（t），x2（t）＜M1．

下面考虑函数W（t）＝x1（t－τ）＋y（t）．计算W沿系统（1）的解的导数，得到

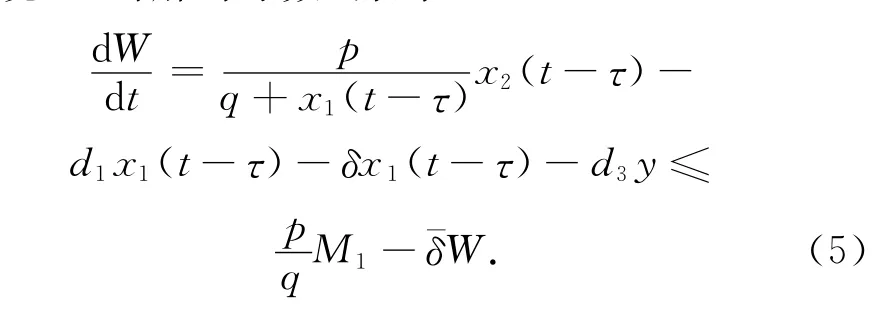
从（5）式知，存在正数M2，当t充分大时，有0＜W（t）＜M2，从而有y（t）＜M2．定理得证。

2 局部稳定性与周期解

系统（1）总存在平衡点E0（0，0，0）．

0不稳定；

0近稳定。

31界平衡点是不稳定的；ii．当d3＜βx¯1时，平衡点E1是局部渐近稳定的。

证明 1）系统（1）在平衡点E0（0，0，0）处的特征方程为

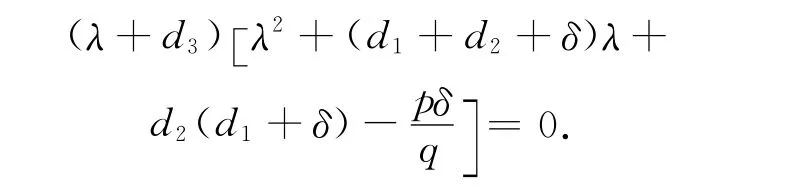
易见，当pδ＞qd2（d1＋δ）时，E0（0，0，0）是一鞍点；当pδ＜qd2（d1＋δ）时，平衡点E0（0，0，0）局部渐近稳定。

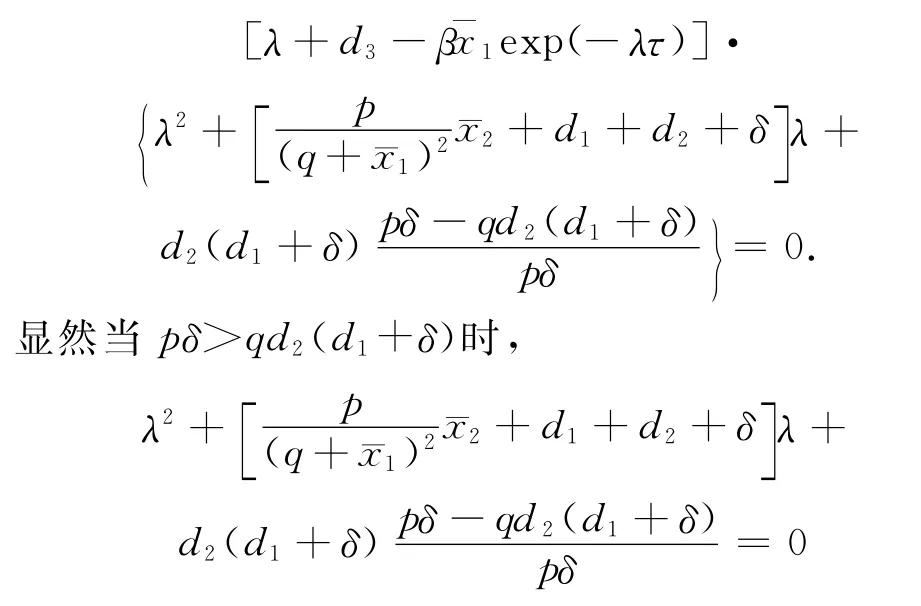
存在两个根λ2＜0，λ3＜0，另一个特征根λ1由λ＋d3－exp（－λτ）＝0的解给出。

i．当d3＞时，注意到y＝λ和y＝的图形必须相交于λ的一个正值，因此平衡点E1是不稳定的。

ii．当d3＜时，方程0的解λ1＜0．因此平衡点E1是局部渐近稳定的。证毕。

证明 系统（1）在平衡点E2（x＊1，x＊2，y＊）处的特征方程为

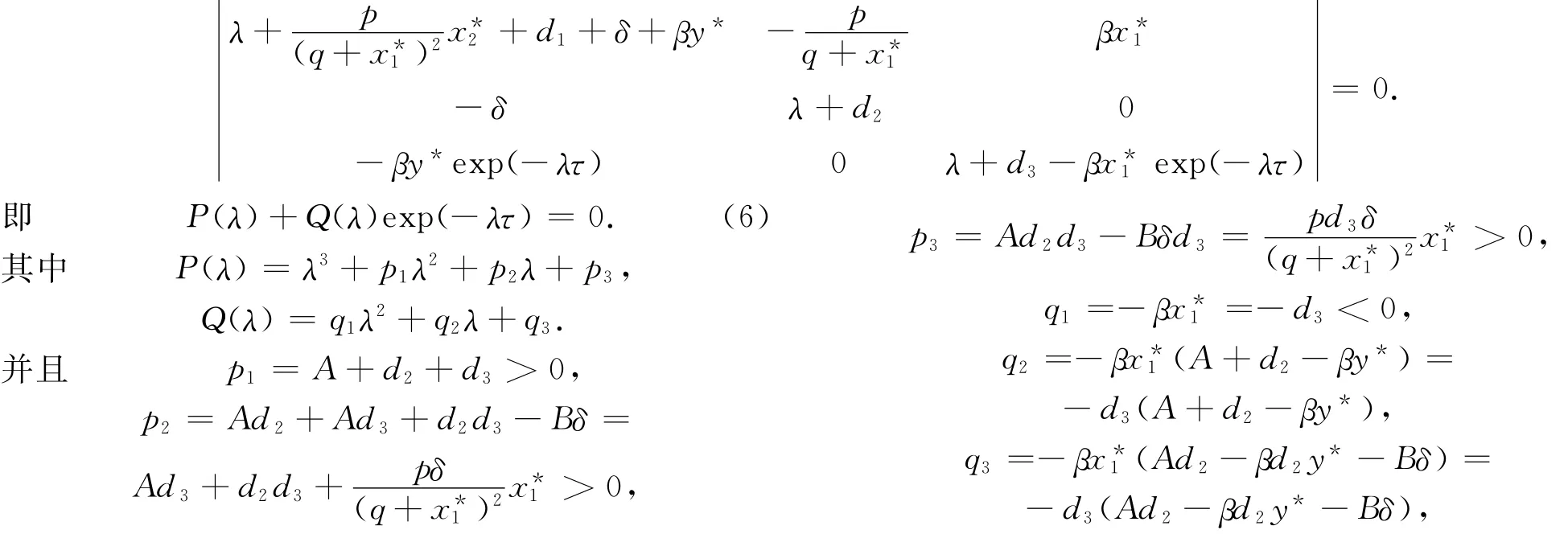
由Routh－Hurwitz准则知方程（7）的所有根均具有负实部当且仅当

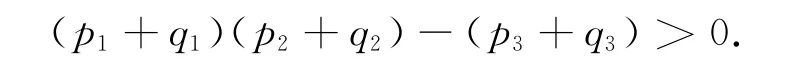
从而当τ＝0或τ很小时，正平衡点E2局部渐近稳定。

证明 首先要证明在平衡点E2处的特征方程（6）有一对纯虚根±iω．

如果λ＝±iω是方程（6）的一对纯虚根，将λ＝±iω代入（6）并分离实部和虚部得：

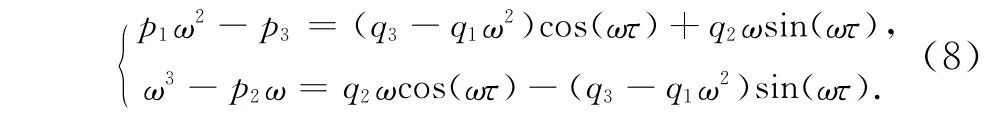
上式两边同时平方并相加得：

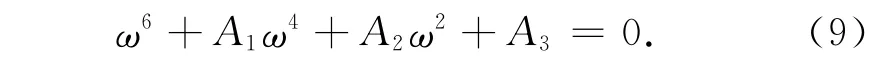
其中，A1＝p21－2p2－q21＝A2＋d22＋2Bδ＞0，

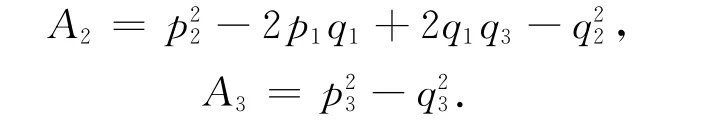
令Ω＝ω2，则式（9）化为

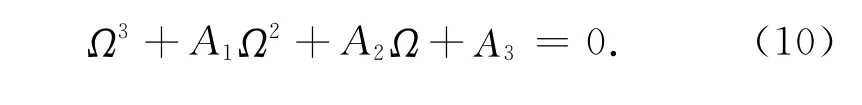
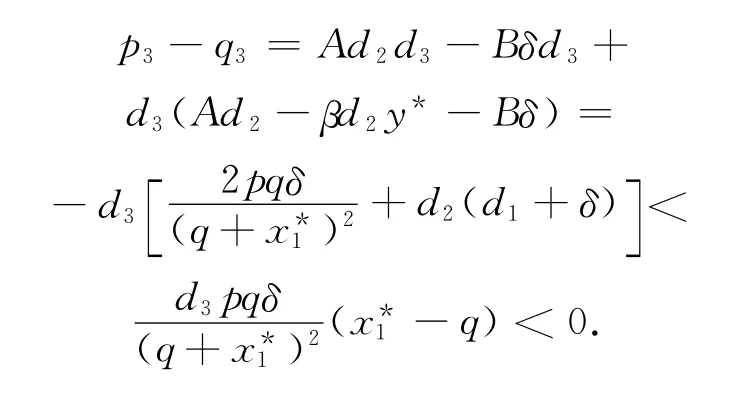
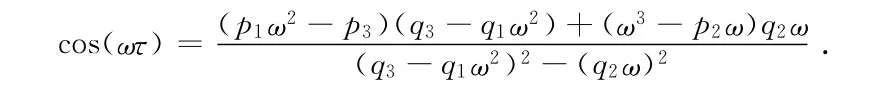
故相应于ω0的τn由下式给出：

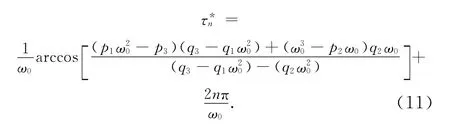
因为τ＝0时，E2局部稳定，从而由Butler引理［9］知，在定理的条件下，平衡点E2对所有的τ≤τ0（τ0＝τ＊0，n＝0）仍是局部渐近稳定的。由于（11）有唯一正根，根据Cooke［10］的结论，下列横截条件成立：

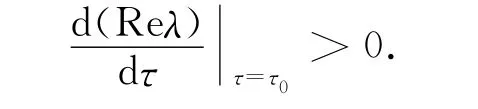
事实上，对（6）两边同时求导得：

3 全局稳定性

类似文献［11］中定理3．2的证明，得到下列定理。

定理5 当pδ＜qd2（d1＋δ）时，平衡点E0（0，0，0）全局渐近稳定。

定理6 若pδ＞qd2（d1＋δ）和d3＜满足，并且βM1＜b3，则系统（1）的边界平衡点E1是全局渐近稳定的。这里M1如定理1中所述。

证明 由于满足pδ＞qd2（d1＋δ）和d3＜，系统（1）的边界平衡点E1是局部渐近稳定的，我们只需

首先考虑系统（1）的第三个方程。可得：

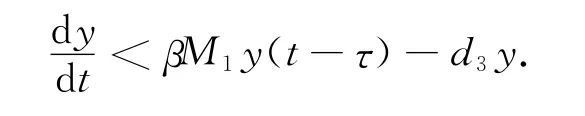
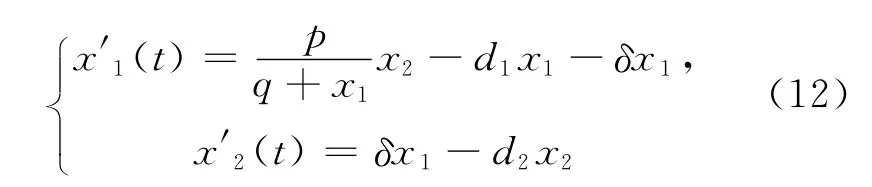
作时间参数变换。设dt＝（q＋x1）dτ，则系统（12）变为

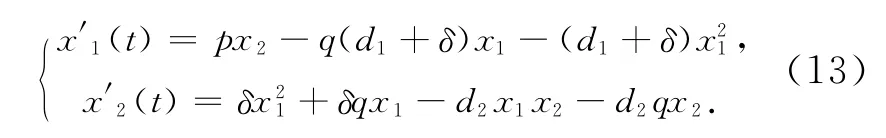
作量纲一变换：

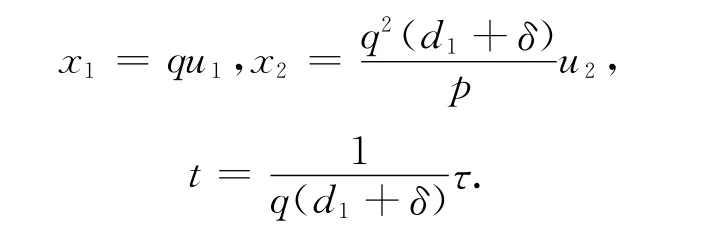
则系统（13）变为

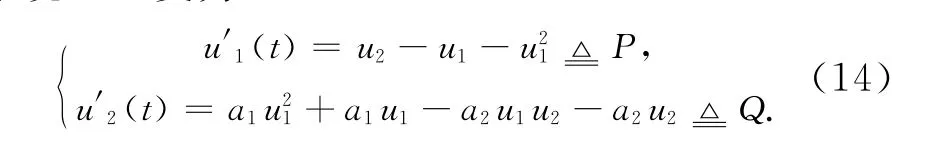
当pδ＞qd2（d1＋δ），即a1＞a2系统（14）有2个非负平衡点），且（0，0）总是一鞍点是局部渐近稳定的。其中

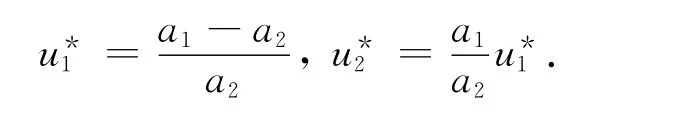
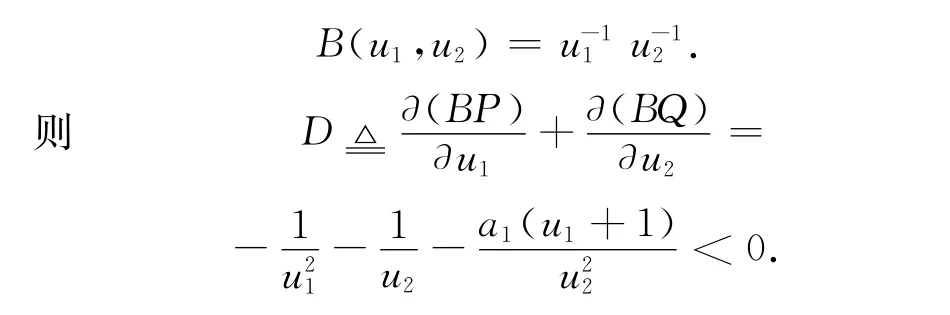
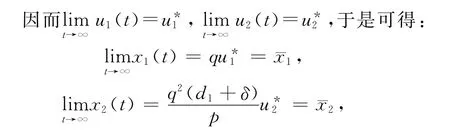
证毕。

［1］ Aiello W G，Freedman H I．A time－delay model of single－species growth with stage structure［J］．Math Biosci，1990，101：139－153．

［2］ Chen Fengde．Permanence of periodic holling type predator－prey system with stage structure for prey［J］．Applied Mathematics and Computation，2006，182：1849－1860．

［3］ Wei Fengying，Wang Ke．Permanence of variable coefficients predator－prey system with stage structure［J］．Applied Mathematics and Computation，2006，180：594－598．

［4］ Wei Fengying，Wang Ke．Permanence of some stage structured ecosystems with finite and infinite delay［J］．Applied Mathematics and Computation，2007，189：902－909．

［5］ Xu Rui，Chaplain M A J，Davidson F A．Permanence and periodicity of a delayed ratio－dependent predator－prey model with stage structure［J］．Math Anal Appl，2005，303：602－621．

［6］ Xu Rui，Wang Zhiqiang．Periodic solutions of a nonautonomous predator－prey system with stag structure and time delay［J］．Journal of Computation and Applied Mathematics，2006，196：70－86．

［7］ 师向云，郭振．一类具有时滞和阶段结构的捕食系统的全局分析［J］．信阳师范学院学报：自然科学版，2008，21（1）：32－35．

［8］ 黄旭玲，文玉婵．非线性生育率的阶段结构系统的定性分析［J］．玉林师范学院学报：自然科学版，2004，25（5）：1－3．

［9］ Freedman H I，Sree H R V．The Trade－off between mutual interference and time lags in predator－prey systems［J］．Bull Mathe Biol，1983，45：9912－1003．

［10］ Cooke K L，Van D D，Riessche P．On zeros of some transcendental functions［J］．Funkcial Evac，1986，29：77－90．

［11］ Xiao Yanni，Chen Lansun．A ratio－dependent predator－prey model with disease in the prey［J］．Appl Math Comput，2002，131：397－414．