基于Fluent的具有防渗墙堤基的渗流场数值模拟分析
张 瑜,李治勤
(太原理工大学 水利科学与工程学院,太原030024)
江河堤防是防洪体系的基础,是防洪保安的重要屏障,但多数堤防是人力填筑,坝身及堤基缺乏可靠的渗流控制措施是历年汛期发生险情的重要原因。在堤防加固过程中,掌握堤身工作及地基的渗流特点,采用合理的渗流控制措施是确保堤防安全度汛的重要前提[1]。渗流对水利工程的影响是多方面的,其中主要是渗透变形或渗透破坏,这种渗流问题对水利工程影响最大。河道溃口出现的原因大多是由于渗透破坏所致,只要河道中堤防的临水侧和背水侧存在水头差,堤防就会有渗流发生。当产生渗流的渗透比大于土的临界比时,土体将产生渗透破坏[2]。
在各种地基基础上堤防经过渗流计算,当堤防地基背水坡或堤后地面渗流出溢点不能满足规范要求,或经汛期曾出现过严重的渗漏管涌、流土破坏时,应采取除险加固措施。目前,经常采用的堤防渗流控制措施主要有三类,即垂直防渗墙、水平压盖技术和减压井技术。垂直防渗措施技术主要适用于强透水层厚度不大于二元结构堤基和防渗依托层埋深较浅且厚度较大的多元结构堤基[3]。
研究水利工程中的渗流问题的方法很多,归纳起来可分为三类,即基于各种公式计算渗流特性的理论方法、基于绘制流网图确定渗流特性的图解方法和利用模拟原理确定渗流特性的数值模拟和物理模拟实验方法[4]。数值模拟法又称为数值法,随着计算机的高速发展,这种方法应用的越来越广泛。Fluent是模拟复杂渗流场较为理想的软件,其采用有限体积法划分网格和建立离散方程[5]。Fluent的多孔介质模型在渗流问题方面有着很好的模拟结果,杨海英[6]等采用该软件模拟了金沙峡电站坝区的渗流场,宋永占[7]模拟了重力坝渗流场,而对于具有防渗墙的河道堤防的防渗效果的分析还很少见,应用Fluent软件进行渗流计算时,程序所能计算的网格数比应用有限元法计算时所能够计算的网格数大很多,计算速度快且精度高。笔者采用FLuent数值模拟方法分析堤基无防渗墙与采取防渗墙措施情况下的渗流场情况,综合分析防渗墙不同深度下的防渗效果,为采取防渗控制措施提供依据,对促进渗流分析技术的发展具有重要的意义。
1 计算模型及工况
1.1 计算模型
笔者针对某河道治理工程中堤防防渗问题,堤防背水面地下水位在设计河底水平面以上0.5m,河道蓄水位2m,如图1,计算区域为含防渗墙浆砌石堤防下沿河道横剖面方向的矩形二维剖面区域,计算区域的深度取10m,按半无限地基计算,计算区域的宽度取22m。假定浆砌石堤防与防渗墙均不透水,模型底面为不透水边界,其他面边界条件指定为墙,堤防内侧设计河底水平面为已知压力进口的边界条件,堤防背侧与设计河底齐平的水平面设定为已知压力出口的边界条件,整个计算区域设定为fluid区域,在进行求解时设定为多孔介质模型。
按四边形网格进行单元剖分,区域划分见图1。
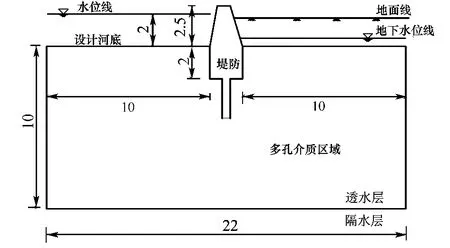
图1 计算模型无网格示意图(单位:m)
对于防渗墙不同深度的坝基渗流区域建立物理模型并划分网格后设置计算模型,采用Fluent6.3.26默认的求解器及运行参考压力。黏性模型为层流模型,速度压力耦合公式采用求解压力耦合方程组的半隐式方法即SIMPLE算法,欠松弛银子和离散格式等采用默认值,计算的收敛精读采用默认值0.001。
1.2 计算工况
按照上述方法建模,划分网格,设置求解模型,输入相关参数,分别对防渗墙深0,2,2.5,3,3.5,4,4.5,5,5.5,6m 的工况进行渗流场的数值模拟。
2 多孔介质模型的设置及参数的选取
多孔介质模型进行设置时应设定穿越多孔介质的流体,并为渗流流体指定方向,使用笛卡尔坐标系定义系数的基本方法是在二维问题中定义一个方向矢量,在三维问题中定义两个互相垂直的方向矢量[8]。本文的二维渗流场指定一个沿剖面垂直向下的矢量作为需要的方向。另外需要根据实际情况定制多孔介质的孔隙率及相关阻力系数,
根据渗流理论达西定律的表达式为:
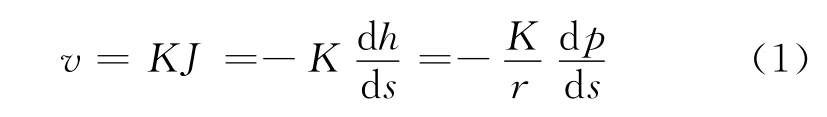
对Fluent计算程序,达西定律表达为:
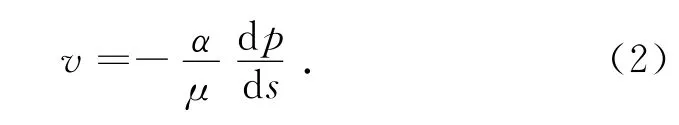
式中:K为渗透系数;J为渗透坡降;h为水头;p为渗透压力;s为渗径;r为水的容重。因此,
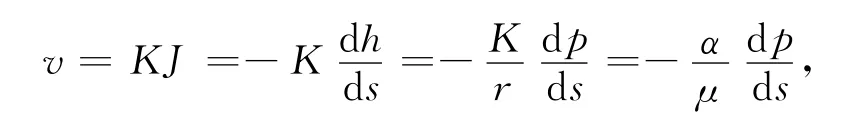
可以推出:
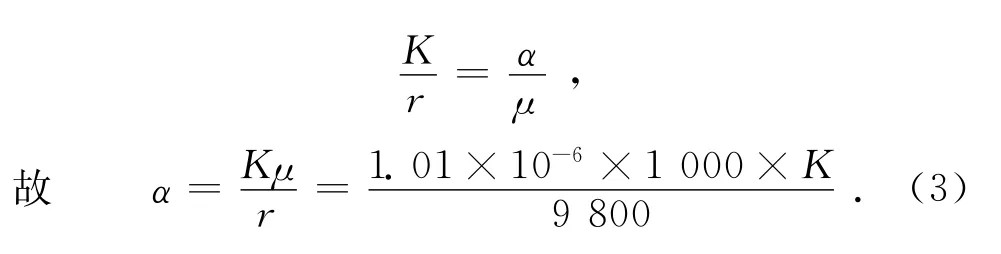
本文涉及的坝基渗流场,由于流体流速慢属于层流运动,可忽略其惯性损失项,因此,运用有限体积法多孔介质模型计算渗流场时,整个渗流场的地质条件仅由参数α确定和区分[9]。文中渗透系数K=1.5×10-4m/s,代入式(3)中得α=1.55×10-11,因此多孔介质模型中1/α=6.45×1010。
3 计算分析的理论依据
当含水层中各点的运动要素(如水头及流速)与时间无关时,称为稳定渗流,反之各点的运动要素与时间有关则为非稳定渗流,将达西定律代入连续性方程则可得不可压密介质中的渗流基本方程即为稳定渗流微分方程:
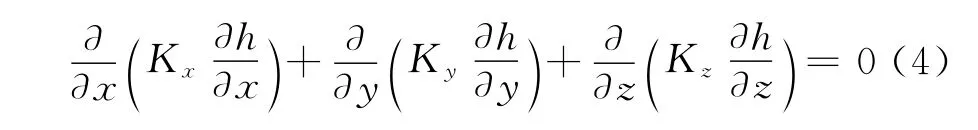
当各向渗透性为常数时,上式变为:
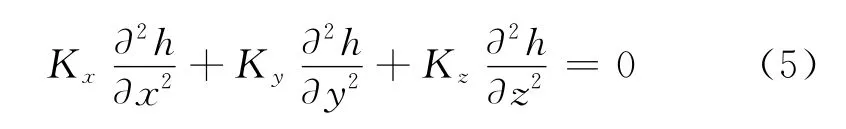
若为各向同性时,上式变为拉普拉斯方程:
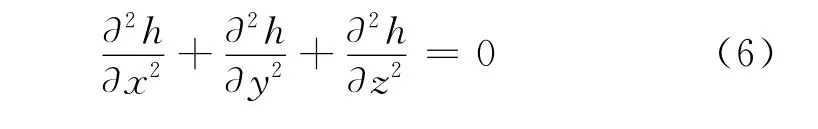
4 模拟结果及分析
堤防的渗流变性主要是管涌,流土,接触冲刷等渗流变形,因此,对堤防渗流场分析主要是研究堤防背水侧的渗流稳定。渗流速度与渗流量是堤防渗流分析的主要内容,通过对不同防渗墙深度工况下堤防的渗流场数值模拟,可得出堤基背水侧渗流场出口截面速度散点图,举典型的四种工况如图2所示。
堤后表层或者浅部弱透水层底面承受的水头压力超过该底面以上土层的重量后会造成土层的隆起和抬动,此即抗浮稳定问题[10],因此,对堤防渗透破坏来说,在模拟分析研究堤防渗流场时,除了考虑渗流速度和渗流量外,还应研究堤防地基基础受到的扬压力。通过模拟分析可得不同防渗墙深度下堤防渗流场的等压线图,举四种典型的工况如图3所示。
由防渗墙不同深度时渗流场的出口截面速度图及等压线分布图可得出渗流量及扬压力与防渗墙深度的关系曲线如图4和图5所示。
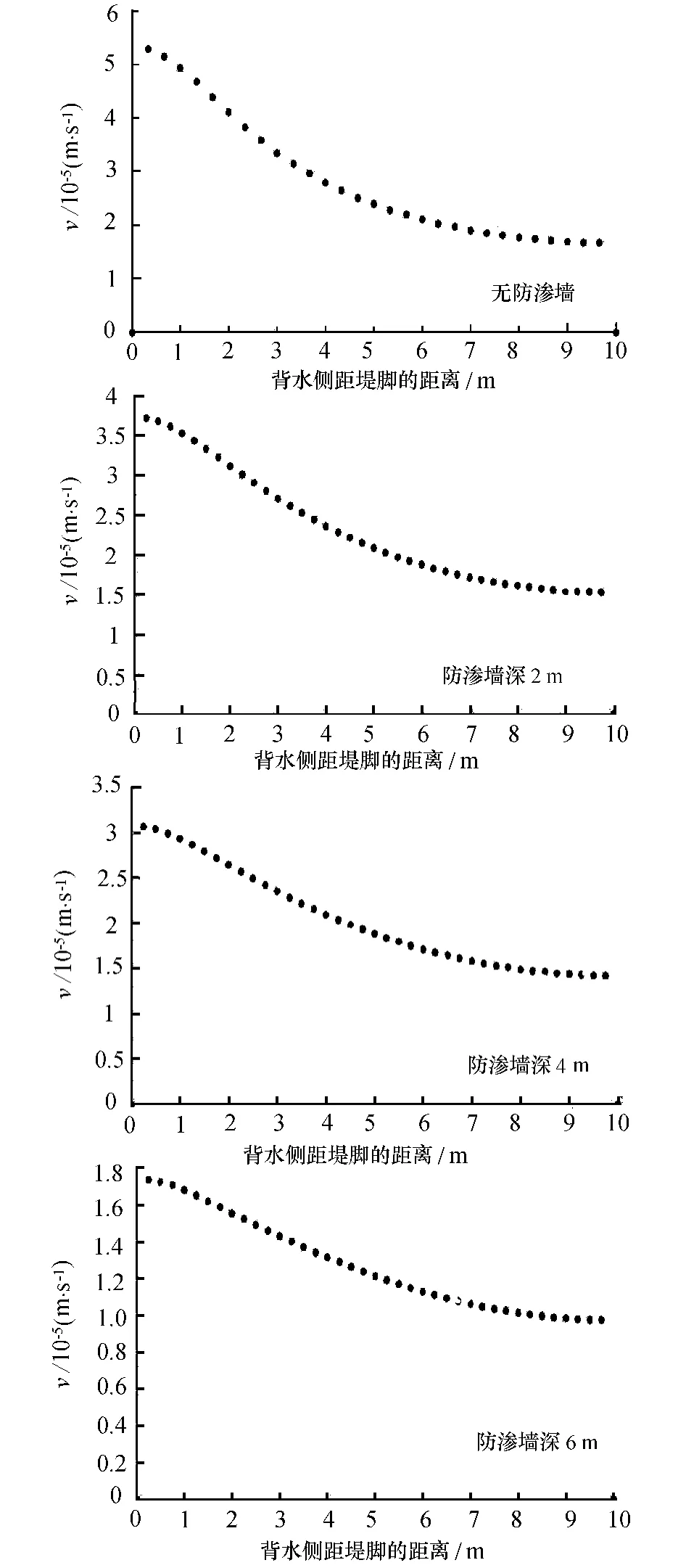
图2 不同深度防渗墙渗流场出口截面速度分布
图中F0和Q0为没有防渗墙时的堤基渗流量和扬压力,此值作为比较的参考值,F和Q为设置防渗墙时数值模拟出来的扬压力和渗流量,文中主要在F/F0和Q/Q0之值的基础上进行分析研究,以便于对结果进行定性分析。
根据上述数值模拟的结果,F/F0和Q/Q0随防渗墙深度的变化如表1所示。
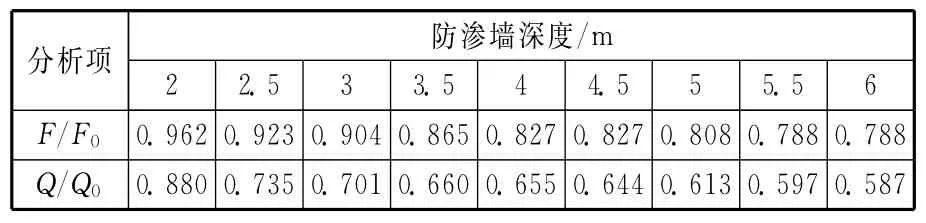
表1 模拟结果
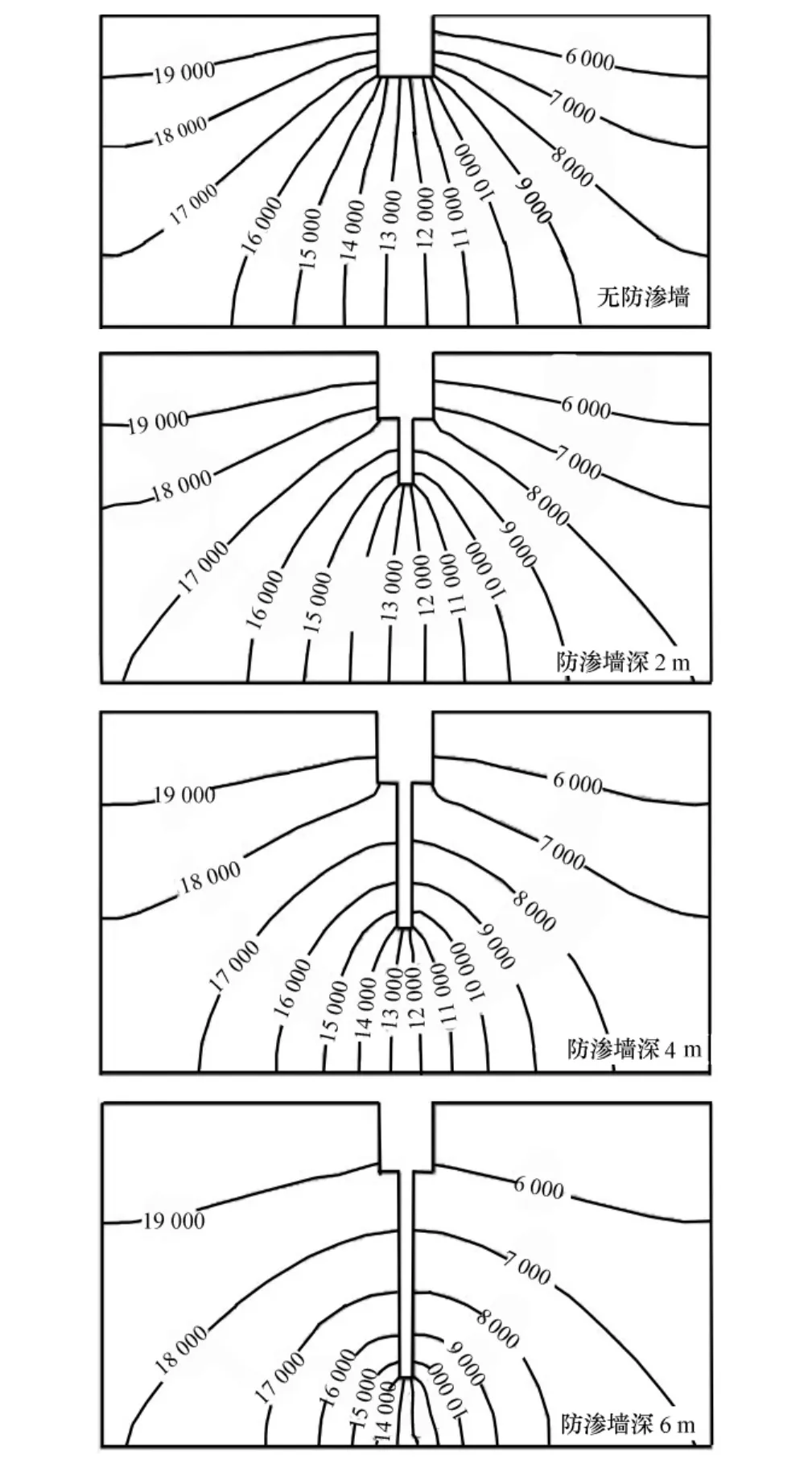
图3 不同深度防渗墙渗流场出口截面压力分布
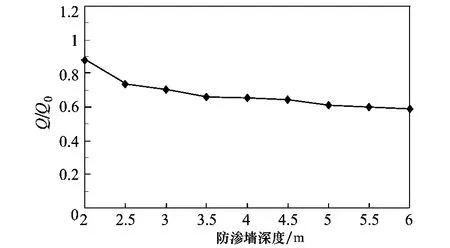
图4 防渗墙深度与渗流量关系曲线
由图2~5与表1可得:
1)防渗墙变深时,堤防背水侧的溢出点距堤基变远,延长了渗径,堤基的渗流量和扬压力都得到了有效的消杀,曲线都有下降的趋势。扬压力比值降低幅度最大达0.788,渗流量比值降低幅度最大达0.587,由此说明防渗墙对降低渗流量十分有效,对于降低扬压力的作用效果较弱。
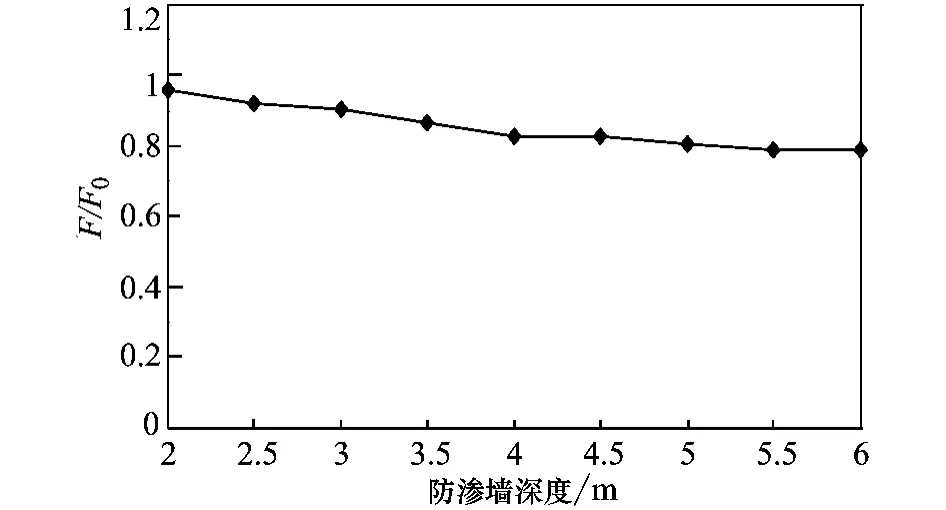
图5 防渗墙深度与扬压力关系曲线
2)防渗墙深度越大,曲线趋势趋向平缓,扬压力及渗流量的值变化微弱,甚至不再改变。这说明防渗墙的深度所起的防渗作用不是无限制的,而是存在一个合理的深度,对于本文讨论的深10m的均质各向同性的堤基推荐防渗墙深度5m。
5 结论
通过对具有防渗墙堤防的渗流场数值模拟及分析,现得出如下结论:防渗墙对堤防渗流量及扬压力具有良好的防渗效果,防渗墙深度达到一定时渗流量及扬压力变化微弱,说明防渗墙在防渗工程中具有一定的合理深度。本研究为河道工程中的渗流问题提供了参考及依据。
[1] 刘铁龙.堤防渗流控制特点及其设计[J].西北水电,2004(04):36-40.
[2] 赵勇,魏虹.河道堤防除险原因及整治方法[J].农业工程,2004(02):48-49.
[3] 罗茜文.堤防渗流控制技术研究发展[J].节水灌溉,2012(5):52-55.
[4] 苑莲菊.工程渗流力学及应用[M].北京:中国建材工业出版社,2001.
[5] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2006.
[6] 杨海英.采用有限体积法进行闸坝堤基渗流分析与防渗措施研究[D].西安:西安理工大学,2005.
[7] 宋永占.基于有限体积法的砼重力坝坝基防渗排水措施分析研究[D].兰州:兰州理工大学,2011.
[8] 韩占忠.Fluent流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2008.
[9] 钟小彦.基于介质模型和VOF法渗流场数值模拟[D].西安:西安理工大学,2010.
[10] 刘心岩.堤防渗流状态及防渗墙结构型式分析[J].黑龙江水利科技,2004(07):3-5.

