最优有界控制下色噪声驱动多时滞拟线性系统瞬态响应*
戚鲁媛,徐 伟,高维廷
(1.西北工业大学理学院,陕西 西安 710129;2.西北工业大学电子信息学院,陕西 西安 710129)
引 言
随机因素在自然界中广泛存在。随机振子的响应问题是理论研究及工程应用中的热点问题[1~3]。瞬态响应是响应问题的一个重要方面,研究系统的瞬态响应可以从时域方面诠释随机振子的运动性态。Fokker-Planck-Kolmogorov(FPK)方程方法是扩散过程理论的主要方法,通过求解FPK方程得到系统的转移概率密度可用以分析系统响应控制、信息熵等问题[4,5]。由于FPK方程的复杂性,只有少数特殊的系统具有理论精确解[6]。虽然相关领域的学者们在稳态FPK方程理论求解方面进行了大量的研究工作[7,8],但瞬态FPK方程的解仍是极难解决的一个问题,目前只能借助理论分析与数值计算 相 结 合 的 方 式 进 行 近 似 求 解[9,10]。1968 年,Bhandari和Sherrer首次应用Galerkin法求解FPK方程的平稳解[11],而后 Wen将其发展到求解FPK方程的瞬态解[12]。2007年,Spanos结合基于等价线性化的随机平均法和Galerkin法研究了白噪声激励的非线性系统的瞬态响应[13]。
时滞现象广泛存在于物理、生物和控制等自然科学与工程实践领域中。研究瞬态响应概率密度时考虑到时滞的作用具有重要的理论及实践意义。文献[14]中基于广义谐和函数随机平均法和Galerkin法研究了白噪声激励的时滞强非线性系统的瞬态响应。虽然白噪声模型在理论上便于处理,但研究表明实际噪声模型应为有色噪声。与有色噪声相关的研究工作已经渗入到随机动力学的各个分支:文献[15]中研究了色噪声激励下非对称双稳系统的平均首次穿越时间,文献[16]中研究了色噪声激励的双稳 Duffing-Van Der Pol振子的随机分岔,文献[17]中研究了色噪声激励的非线性系统的稳态响应,文献[18]中研究了非高斯色噪声作用下 Van Der Pol-Duffing振子的稳定性。但是,色噪声激励的时滞非线性系统的瞬态响应相关研究却少见报道。当系统中含有时滞与非白噪声时,随机平均法是一种有力的理论分析工具。该方法不但可以避免非白噪声引起的FPK方程的扩维现象,而且可以降低FPK方程的维数,从而简化理论分析和数值计算。
考虑到工程安全,瞬态响应需要被控制在安全范围内,因此考虑瞬态响应的最优控制问题是非常有必要的。鉴于实际控制器发生装置只能产生有限的控制力,故而研究最优有界控制是符合工程实际的。很多学者已经关注到随机非线性振子的最优有界控制问题,例如文献[19]中利用最优有界控制率成功地降低了系统的稳态响应。然而基于瞬态求解FPK方程技术研究随机时滞拟线性系统的最优有界控制问题未见报道。
综上所述,本文提出了色噪声激励的时滞拟线性系统瞬态响应的最优有界控制问题。将时滞系统转化为等价的非时滞系统后应用标准随机平均法得到振幅过程的部分平均Itô随机微分方程。再由动态规划准则导出最优有界控制率进而得到完全平均的FPK方程。利用Galerkin方法近似求解此FPK方程即得到系统近似瞬态响应。最后将该方法应用到受最优有界控制率作用的色噪声激励的时滞Duffing-Van Der Pol振 子 得 到 理 论 解,并 利 用Monte-Carlo模拟方法证明理论解的有效性,利用该方法综合讨论了色噪声、时滞和控制力参数以及共振对瞬态响应的影响。
1 模型提出和化简
色噪声激励多时滞拟线性受控系统的方程为


1.1 时滞化简
假设存在小量δ,当ξ0,H,F和u为δ阶小量且fkSk(ω)为δ1/2阶小量时,系统(1)是拟线性系统[20],采用标准随机平均法,引入如下变换




利用式(3)和(4),系统(1)可转化为如下非时滞系统

1.2 部分平均Itô随机微分方程
将式(2)代入式(5)得到A(t)和Θ(t)的方程组,如下

式中m1,m2,σ1k和σ2k的具体表达形式为:

由式(6)中第1式的系数m1(A,Θ)和σ1k看出,关于A(t)的微分方程不显含Θ(t),故A(t)收敛于一维Markov扩散过程[22]

式中B(t)为单位维纳过程,且

方程(10)对应的FPK方程为

方程(14)的初始条件设为

2 最优有界控制和完全平均FPK方程
振幅可以代表系统响应程度,降低振幅可降低系统响应。以减小振幅为目标,在[0,tf]上考虑最优遍历控制,假设控制力满足如下约束条件

式中u0表示控制力界值。

值函数为

由动态规划准则和式(10)[23],得动态规划方程为

终值条件为



将式(21)代入式(11)并按式(13)完成所有平均过程,得到如下完全平均的漂移系数

将式(22)代入式(14)即得到全平均FPK方程。
3 FPK方程近似瞬态解
3.1 正交基空间
首先考虑系统(1)的退化线性系统
通过化学与生物活性相结合的筛选模式得到真菌Penicillium sp. H1,这株菌主要代谢产生二萜类物质,即3个二萜类化合物(1~3),其中化合物1为新化合物。发现化合物1和2有中等强度的香蕉枯萎病菌抑制活性(MIC分别为32.0和16.0 μg/mL)。结果表明海洋来源的青霉作为生物活性物质的来源具有进一步研究和开发的价值。

在式(22)中令u0=0,H=0,F=0并代入式(14)得到退化线性系统的FPK方程为
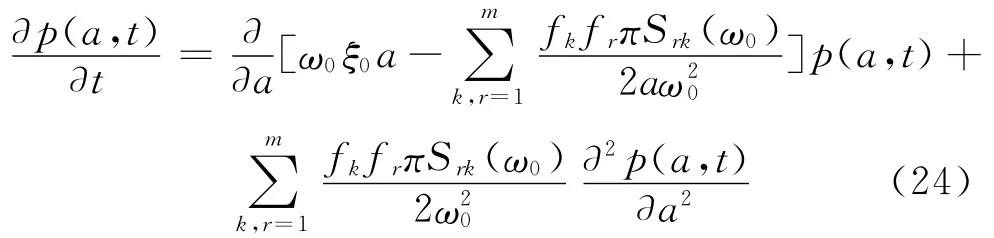
由FPK方程本征函数法得关于式(24)的本征方程[24]

式中λn为特征值,Zλ为特征函数。

式(26)满足Laguerre多项式微分方程,由此可得一组特征值λn和基函数An:

式中Ln(·)表示第n阶Laguerre多项式。
由式(28)和Laguerre多项式性质得基函数满足

式中δj,n是 Kronecher Delta符号。
式(24)的解可以表示为

3.2 近似瞬态解
首先将式(14)的解近似写成如下形式

将式(31),(32)代入式(14)并整理得如下误差参量:


将式(33)代入式(34)并结合式(30)进行化简得到关于cj(j=0,1,…)的常微分方程组如下:

联合式(15),(32)可得式(35)的初始条件:cj=0。
系统j阶响应矩表达式为

4 算例分析
本章用一个例子具体分析理论求解过程。色噪声模型为高斯白噪声的二阶滤过过程,表示为

式中和βk为正常数,Wk(t)为零均值且强度为2Dk的高斯白噪声,色噪声(37)的谱密度为

令

式中ω0和ξ0与式(1)中相同;a1,a2和β0均为常数,ε为正常数表示非线性阻尼强度。考虑一个色噪声激励的情况,即f1=1。将式(21),(39)和(40)代入式(1)得到最优有界控制率作用的色噪声激励的双时滞Duffing-Van Der Pol振子

4.1 理论分析
将式(39)和(40)代入式(22)整理可得

由式(14)得与系统(41)相应的FPK方程为

由式(27)~(29)得到相应的特征值和基函数为:

由式(33),(39),(40)得相应的误差参量为

结合Laguerre多项式的性质得到如下化简关系式:
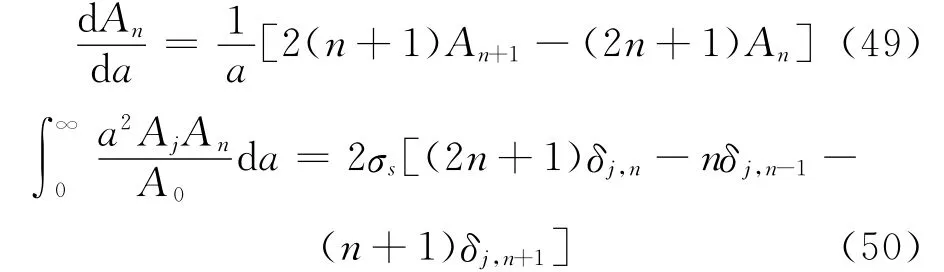
将式(39),(40)代入式(35)并利用式(49),(50)化简最终得到关于cj(t)的常微分方程组如下:

当cj的下标为负时认为其不存在。实际计算中应当对式(51)进行合理截断以便数值求解,将cj(t)的近似解代入式(32)得到p(a,t)。
4.2 数值分析
本节利用数值计算直观说明色噪声、时滞、控制力参数以及共振对系统瞬态响应的影响,并对系统(1)进行MCS来验证理论求解的有效性。数值计算中固定的系统参数为:ω0=1,ξ0=0.02,β0=0.5,a1=a2=0.01,ε=5。

图1 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0Fig.1 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS: τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0

图2 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0.01Fig.2 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0.01

图3 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0.03Fig.3 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=0.5,u0=0.03
图1~3讨论了控制力参数u0对瞬态概率密度p(a,t)的影响。图1画出了当u0=0时,在式(51)中取21项计算所得的p(a,t)的图像,图2是令u0=0.01并在式(51)中截断到j=20得到的结果,图3是令u0=0.03并在式(51)中截断到j=35得到的结果。如图所示:理论解和MCS解吻合程度好,证明了理论和数值求解的有效性。比较图1~3看出:p(a,t)随控制力增大向左偏移并且此偏移随时间增大越来越明显。随控制力u0增大p(a,t)将集中在较小振幅值范围内并在较小幅值处达到峰值。从概率的观点可以解释为:系统将以较大概率在较小程度响应,即最优有界控制率成功地降低了系统的瞬态响应。正如文献[13]中指出的,当计算的项数达到一定程度时,由计算项数不同而引起的计算误差可忽略。根据本文的数值计算过程发现,当计算项数大于100时,由于计算项数不同引起的误差便可以忽略。当u0由0.03继续增大时(u0≪1),需计算至少30项能得到较好结果,即系统中涉及到的非线性行为越复杂所需要计算的项数就越多。
图2,4和5讨论了在相同条件下,不同的时滞参数对p(a,t)的影响,计算过程中式(51)截断到j=20。以图4作为参考并分析得到:τ1=τ2=4.7(图5)时p(a,t)向左偏移的程度比τ1=τ2=0.5(图2)时p(a,t)向左偏移的程度大,即τ1=τ2=4.7时的系统响应程度较小。在相同控制力作用下,时滞因素使得系统的瞬态响应产生了明显变化,即时滞可以影响控制力的作用。另外,联合式(3),(4)可以得到在平均意义下系统(41)的等效线性阻尼系数为ξ1=ξ0-0.005(cosτ2-sinτ1),即时滞作用主要通过影响系统的线性阻尼部分来影响系统的瞬态响应。

图4 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=1.5,D1=1,□1=3,β1=0.5,u0=0.01Fig.4 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=1.5,D1=1,□1=3,β1=0.5,u0=0.01

图5 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=4.7,D1=1,□1=3,β1=0.5,u0=0.01Fig.5 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=4.7,D1=1,□1=3,β1=0.5,u0=0.01
图6和7讨论了不同色噪声参数对系统瞬态响应的影响,计算过程中式(51)截断到j=20。图6中令□1=3.5其余参数保持与图2中相同,对比图2和6发现:当□1=3.5时p(a,t)明显向左偏移并且在较小幅值达到峰值,从一个侧面说明了适当增大□1可降低系统瞬态响应程度。图7中令β1=1.0其余参数与图2中相同。对比图2和7看出:较大的β1使得p(a,t)集中在较小的振幅值范围内并在较小幅值处达到峰值,这也说明了适当增大β1可降低系统的瞬态响应。综合图2,6和7看出:在相同控制力条件下,适当改变色噪声参数可加强控制力的作用。在工程实践中当控制力有限时,可通过噪声的作用加强控制效果。
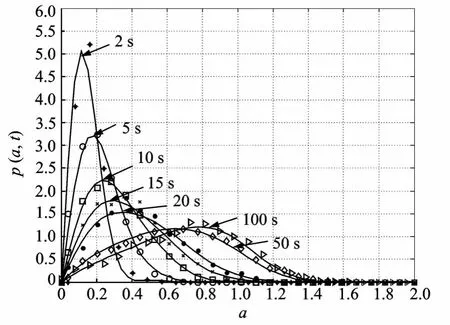
图6 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3.5,β1=0.5,u0=0.01Fig.6 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3.5,β1=0.5,u0=0.01

图7 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=1,u0=0.01Fig.7 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=1,□1=3,β1=1,u0=0.01
图8中给出了当系统频率ω0与激励频率□1相接近时系统的瞬态响应,计算过程中式(51)截断到j=20。由图可见:理论解和MCS解拟合程度高证明了共振条件下理论求解方法的也是有效的。

图8 p(a,t)的曲线,—理论解,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=0.03,□1=1.1,β1=1,u0=0.001Fig.8 Curves of p(a,t),—theory solution,*○□×●◇▷ MCS:τ1=τ2=0.5,D1=0.03,□1=1.1,β1=1,u0=0.001
图1~8的综合讨论说明了文中所提的理论方法可有效计算受最优有界控制的色噪声激励的时滞拟线性系统的瞬态响应。
5 结 论
本文系统地研究了最优有界控制力作用下色噪声激励的多时滞拟线性系统的瞬态响应概率密度。主要包括以下两个部分:(1)引入最优有界控制率来控制色噪声激励的多时滞拟线性系统的瞬态响应,并提出了求解其瞬态响应概率密度的近似方法。该方法包括如下四个方面:首先将时滞方程转化为等价的非时滞方程;其次利用标准随机平均法得到系统振幅过程的部分平均Itô随机微分方程;利用动态规划原理并结合控制力有界的条件导出了最优有界控制率,将其代入部分平均Itô随机微分方程并完成所有平均过程得到完全平均的FPK方程;利用FPK方程本征函数法得到一组正交基空间并在此基空间内进行Galerkin变分得到系统的近似瞬态响应。(2)以受最优有界控制率作用的色噪声激励的Duffing-Van Der Pol振子为算例实现上述求解过程,利用数值计算综合讨论了控制力、时滞和色噪声参数以及共振条件下系统的瞬态响应概率密度并采用MCS证明了所有理论解的有效性。本文涉及的系统是拟线性系统,关于受控的强非线性系统的瞬态响应问题还有待于进一步研究。
[1] 王洪礼,姚士磊,葛根,等.形状记忆合金梁在随机激励下的随机分岔与首次穿越[J].振动与冲击,2012,31(9):24—28.
Wang Hongli,Yao Shilei,Ge Gen,et al.Stochastic bifurecation and first-passage failure of shape memory alloy beam subjevted to stochastic excitation[J].Journal of Vibration and Shork,2012,31(9):24—28.
[2] 孙忠奎,徐伟,杨晓丽.窄带激励下带有时滞反馈的非线性动力系统的响应[J].振动工程学报,2006,19(1):57—64.
Sun Zhongkui,Xu Wei,Yang Xiaoli.Response of nonlinear system to randon narrow-band excitation with time delay state feedback [J].Journal of Vibration Engingeering,2006,19(1):57—64.
[3] 方同.工程随机振动[M].北京:国防工业出版社,1995.
[4] Zhu W Q,Huang Z L,Ko J M,et al.Optimal feedback control for strongly non-linear systems excited by bounded noise [J].Jurnal of Sound and Vibration,2004,274(3):701—724.
[5] Guo P R,Xu W,Liu D.Upper bound for the time derivative of entropy for a stochastic dynamical system with double singularities driven by non-Gaussian noise[J].Chinese Physics B,2010,19(3):030520-1-6.
[6] Caughey T K,Dienes J K.Analysis of a nonlinear first-order system with a white noise input[J].Journal of Applied Physics,1961,32(11):2 476—2 479.
[7] Feng C S,Wu Y J,Zhu W Q.Response of Duffing system with delayed feedback control under combined harmonic and real noise excitations [J].Communications in Nonlinear Science and Numerical Simulation,2009,14(6):2 542—2 550.
[8] Feng C S,Zhu W Q.Response of harmonically and stochastically excited strongly nonlinear oscillators with delayed feedback bang-bang control[J].Journal of Zhejiang University-Science A,2009,10(1):54—61.
[9] Xie W X,Xu W,Cai L.Path integration of Duffing-Rayleigh oscillator subject to harmonic and stochastic excitations[J].Applied Mathematics and Computation,2005,171(2):870—884.
[10]Li J,Yan Q,Chen J B.Stochastic modeling of engineering dynamic excitations for stochastic dynamics of structures[J].Probabilistic Engineering Mechanics,2012,27(1):19—28.
[11]Bhandari R G,Sherrer R E.Random vibrations in discrete nonlinear dynamic systems[J].Journal of Mechanical Engineering Science,1968,10(2):168—174.
[12]Wen Y K.Approximate method for nonlinear random vibration [J].Journal of the Engineering Mechanics Division,1975,101(4):389—401.
[13]Spanos P D,Sofi A,Di Paola M.Nonstationary response envelope probability densities of nonlinear oscillators[J].Journal of Applied Mechanics,2007,74(2):315—324.
[14]Jin X L,Huang Z L.Nonstationary probability densities of strongly nonlinear single-degree-of-freedom oscillators with time delay [J].Nonlinear Dynamics,2010,59(1):195—206.
[15]张娜敏,徐伟,王超庆.色噪声驱动的非对称双稳系统 的平均首次穿越时间[J].物理学报,2007,56(9):5 083—5 087.
Zhang Namin,Xu Wei,Wang Chaoqing.The mean first-passage time for an asymmetric bistable system driven by multiplicative colored and addictive white noise with a correlated noise[J].Acta Physica Sinica,2007,56(9):5 083—5 087.
[16]Xu Y,Gu R C,Zhang H Q,et al.Stochastic bifurecations in a bistable Duffing-Van der Pol oscillator with colored noise[J].Physical Review E,2011,83(5):0562151-6.
[17]吴勇军,朱位秋.色噪声激励下 Duffing-Rayleigh-Mathieu系统的稳态响应 [J].振动工程学报,2009,22(2):207—212.
Wu Yongjun,Zhu Weiqiu.Stationary response of Duffing-Rayleigh-Mathieu system under colored noise excitation [J].Journal of Vibration and Engineering,2009,22(2):207—212.
[18]杨建华,胡栋梁,刘先斌.非高斯色噪声激励下Van der pol Duffing振子的随机稳定性 [J].振动工程学报,2011,24(1):240—250.
Yang J H,Hu D L,Liu X B.The Stochastic stability of a Van der pol Duffing oscillator under a non Gaussian colored noise excitation [J].Journal of Vibration and Engineering,2011,24(1):240—250.
[19]Zhu W Q,Deng M L.Optimal bounded control for minmizing the response of quasi-integrable Hamiltonian systems[J].Internatinal Journal of Non-linear Mechanics,2004,39(9):1 535—1 546.
[20]朱位秋.随机振动[M].北京:科学出版社,1992:285—287.
[21]Feng J,Zhu W Q,Liu Z H.Stochastic optimal timedelay control of quasi-integrable Hamiltonian systems[J].Communications in Nonlinear Science and Numerical Simulation.2011,16(8):2 978—2 984.
[22]Khasminskii R Z.A limit theorem for the solution of differential equations with random right-hand sides[J].Theory of Probability and Its Applications,1966,11(3):390—406.
[23]朱位秋.非线性随机动力学与控制[M].北京:科学出版社,2003:405—407.
[24]Gardiner C W.Handbook of Stochastic Methods for Physics,Chemistry and the Natural Science[M].2nd ed.Berlin:Springer-Velarge,1983.

