船舶噪声源的传递率矩阵识别方法及试验验证＊

张 磊，曹跃云，杨自春，何元安

（1．海军工程大学动力工程学院，湖北 武汉 430033；2．中国船舶工业集团公司船舶系统工程部，北京 100036）

引 言

船舶的噪声源识别或噪声传播途径识别问题是噪声控制中首要的也是最重要的工作［1］。通过振动噪声源识别研究，可以有效估计船舶各个噪声源对水噪声（包括辐射噪声和自噪声）的贡献量，及对噪声源进行相应的空间定位。从而指导船舶减振降噪措施的正确实施和辅助噪声系统的声学设计和噪声预报。另外，当机器或设备出现故障时，其声信号特性一般会改变，因而通过噪声源识别研究，也有助于对机器设备进行状态检测和故障诊断，可以及时地掌握机械的运行状态，准确查找故障，提高船舶的声学性能。

由于船舶结构及其工作环境的复杂性、特殊性，使其具有噪声源耦合强烈、试验实施难度大和测试信号易受环境干扰等特点，使得当前各种方法在实船噪声源识别上的应用往往难以令人满意［2］。目前解决此类噪声源识别问题较为有效的方法是近年来在汽车噪声源研究领域发展起来的传递路径分析（Transfer Path Analysis，TPA）方法［3，4］，但其过程繁琐、试验复杂，且难以准确反映设备在运行状况下的真实振动噪声特性。为了避免上述缺点，一种基于传递率矩阵方法的噪声传递路径分析方法被提出［5］。随着分析中主要应用运行工况时的响应数据，TMM 也被称为工况 TPA（Operational Transfer Path Analysis，OPA）方法［6，7］。即使 TMM 具有众多优点，但在实际工程应用中仍存在3种缺陷［7］：由于结构的模态影响，输入振源间存在交叉耦合缺陷；实际工况的限制可能导致传递特性估计不准确；遗漏部分传递路径，TMM的拟合总值对比不能识别。从TMM实际应用中的缺陷看，有必要对TMM进行改进，在保持效率的同时提高分析准确性。

1 TPA法与TMM的基本原理

TPA方法的基本原理是：机械设备工作状态下辐射声场中的声压响应值等于其与各噪声源之间的频响函数和工作状态下各噪声源处的激励力乘积的叠加［3］，即

式中F（w）为工作状态下的激励力列向量；P（w）为工作状态下声场中声压响应的列向量；HFP（w）为各噪声源到辐射声场中声压响应的频响函数，它不仅是激励频率的函数，还和响应点、激励点的位置有关，但与激励的幅值无关。

直接测量工作状态下的耦合激励力在实际操作中会遇到很多问题，间接测量法不需要嵌入力传感器，这可以在一定程度上避免直接测量法的不足，因而它是工程中常用的方法。逆矩阵法就是一种有效的获取耦合激励力的间接法［3］，该方法需测量力／加速度传递函数，结合实测振动响应X（w），可获得力估计为

以上TPA方法在实际应用中将面临很多问题，不利于工程应用。于是，将式（3）带入式（1）得到基于TMM方程

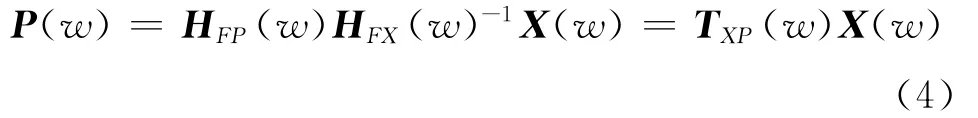
式中 振动输入响应X（w）可以为力信号、振动加速度信号、声压信号、位移信号等。

TMM没有进行载荷识别，而采用响应－响应的方式。由于结构的模态特性，一个激励点的激振力将在其他路径上引起振动，这种输入信号之间有着较复杂的交叉耦合关系很容易导致主要路径的识别错误。对于该问题，实际应用中主要结合一些先验信息（如设备的特征频率等），选取紧挨振源且振动响应较大，并能反映振源频率较全面的振动加速度测点作为振源输入。对于耦合性较弱的振源是可行的，但振源耦合性较强或振源测点在共振和反共振频率时却很难得到理想的效果。由式（1）和（2）可知，为了避免输入振源之间的交叉耦合性，需满足频响函数矩阵HFX（w）为对角矩阵，即每个路径处的振动响应X（w）仅与相应的激励力有关。在船舶机械设备振源特性分析时，1kHz以下的低频段内，可将机械设备和基座以及整个减振器的接触单元认为是点接触［8］。根据复刚度法［3］，主动方（设备）与被动方（基座）中间通过弹性件（隔振器）连接，耦合连接件与主动方和被动方的两端连接处都产生位移。机械设备通过隔振装置作用到基座，其工作力按下式求得

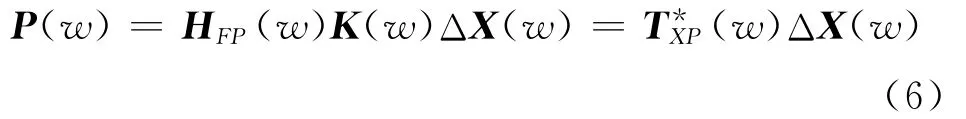
此处将隔振器两端的位移响应之差ΔX（w）视为输入振源，因HFX（w）－1＝K（w），可知HFX（w）为对角矩阵，即振源ΔX（w）在一定程度上避免了输入振源之间的交叉耦合性。且只需要输入输出的加速度响应来求得传递函数矩阵（w），而不需要获得复刚度矩阵K（w）或频响函数矩阵HFX（w）。

TMM关键的一个部分就是计算系统的传递特性矩阵（w），该矩阵里所有元素都是从同一次试验数据中得到的，所有的输入都是在同一时刻进行的，将式（6）两边取转置得

式中m，n表示输入输出的自由度数。如果定义船体结构系统的传递函数矩阵是线性时不变的，对于r个不同的测量工况满足

TMM是一种理论简单且快速的方法，该方法仅需要运转工况时振源响应和目标点的声压响应值。利用在不同工况下由振源测点到目标点的声压响应所形成的传递矩阵，即可分析每一个传递路径对目标点的贡献，进而识别出主要噪声源。但实际工程应用中有效地实现TMM是非常困难的，仍面临以下问题：

（a）输入信号之间的相干性以及实际工况的限制产生病态矩阵求逆等问题，可能导致不可靠的传递特性估计。可采用截断总体最小二乘（TTLS）方法避免矩阵求逆存在的不适定问题［9］，TTLS考虑了振源输入矩阵ΔX和声压目标点矩阵P同时存在测量误差，优于传统的基于最小二乘（LS）的奇异值截断方法。

（b）遗漏部分传递路径，TMM合成总贡献不能识别。可用重相干函数检测是否有重要传递路径被遗漏［10］，假设本文路径数目均已知。

2 船舶振动－声辐射仿真计算及结果分析

利用CAE技术进行船舶结构振－声耦合计算，以验证TMM在船舶噪声源识别中的可行性与正确性。利用ansys创建船舶结构有限元模型（船长15 m，最宽处2．5m，高1m），如图1所示。假设舱段内有5台机械设备，设备1#，2#，3#在同一个舱段内，将振动设备等效为集中质量系统，在集中质量系统上施加的激励载荷，每个集中质量系统通过4个弹簧－阻尼单元与甲板相连。利用Virtual．Lab对船舶辐射噪声声场指向性和辐射噪声衰减进行仿真计算，可知与船舶夹角130°的轴线位上有最大辐射声压幅值。同时通过船舶辐射噪声衰减仿真结果，与船舶垂直距离50～100m范围内的声场均满足球面波衰减规律（远场测量条件）。综上，此次仿真将声场测点位置选为轴长100m，与船夹角130°处。

基于Virtual．lab软件进行船舶部分浸入水中（吃水深度0．5m）的声振耦合计算，即先把声场的一部分离散成声学有限元网格，进行声固耦合声学有限元分析，接着在声学有限元网格的外表面上定义声学无限元，然后定义场点网格。最终获得船舶振动响应和声场中的声压响应，为贴合工程实际，数据处理时将加入随机噪声的影响。工况包括5台振动设备同时作用和每个设备单独作用，分析频率f＝20～300Hz。

图1 船舶结构有限元模型Fig．1 Finite element model of the ship structure

2．1 声场噪声合成与验证

模型中一台设备有4个机脚与甲板相连，选择设备均布置规则且测点位置对称。在低频范围内，通过设备单独开启，检测设备各机脚测点振动响应之间的相干性，检测发现：单个设备各测点之间在关注的频段内相干性均较强（＞0．8），此时可选择任一一个测点作为振源输入，为保证信噪比，选择振动响应最大的测点。再利用1节中提到的重相干系数检测所有设备的振源测点对声场目标点的相关性，在关注的频段内各振源与目标点的重相干系数值均＞0．8，即可认为所选振源测点能够反映目标点的所有信息［10］。通过 MATLAB编制TMM程序对5个振源在某一工况下到船外目标点声压贡献量进行合成，基于两种输入振源的合成值与实际值均吻合非常好，如图2所示。由于测得的数据在模型计算中被应用了两次，合成声与实测噪声吻合较好并不能一定保证TMM的有效性。例如：由图3，4可知，以加速度作为振源时，尽管总合成声与实际吻合较好，但单条路径对目标点的响应与实际值偏差较大。可见，只有在解决了1节中的几个关键问题，结果才是可信的。假如不理解TMM的原理，将很容易被结果误导。而本文以ΔX（w）作为输入振源建立的模型在有效地解决了TMM应用中面临的关键问题，结果可信，也证明了船外噪声传递路径模型和仿真计算模型的正确性。

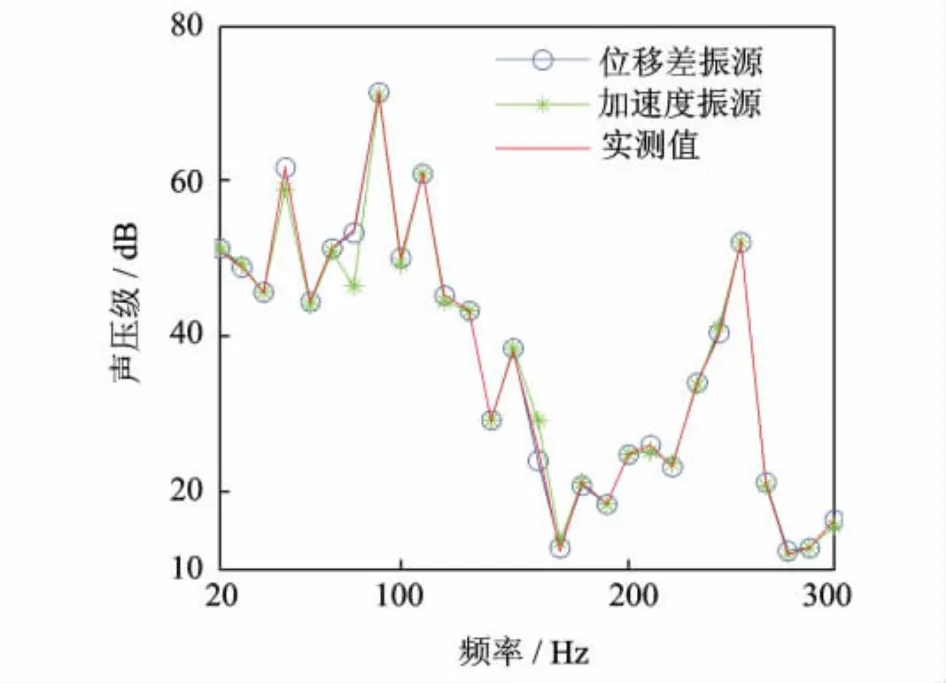
图2 噪声实测值与合成值比较Fig．2 Contrast of synthesized and actual noise

2．2 噪声贡献量分析

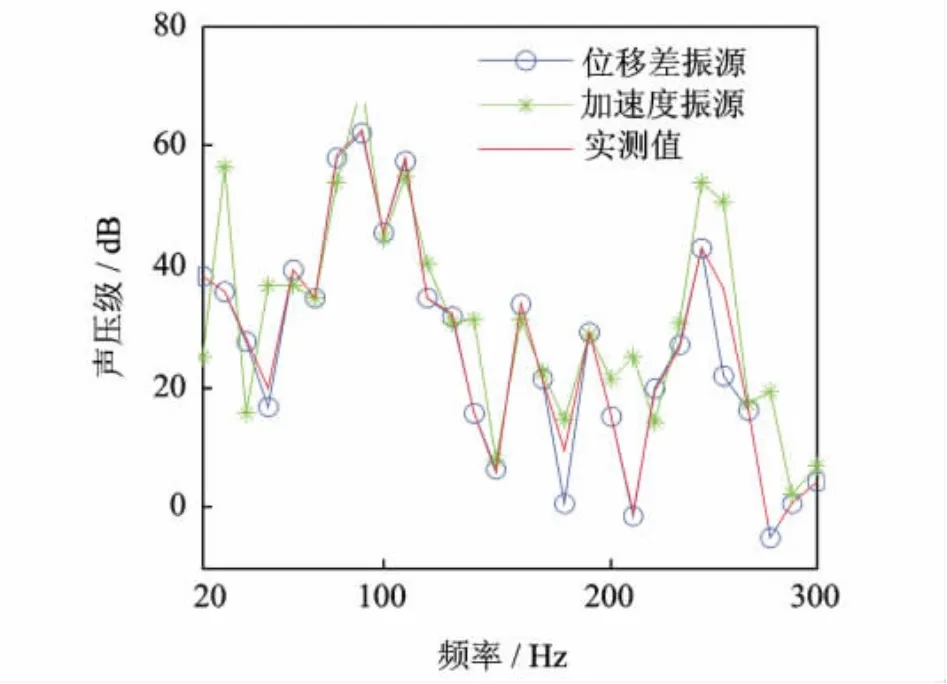
图3 1#设备合成和实测噪声对比图Fig．3 Contrast of synthesized and actual noise of 1#

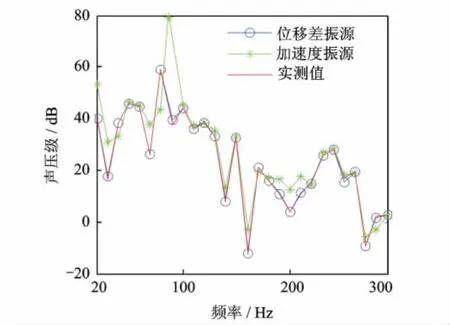
图4 5#设备合成和实测噪声对比图Fig．4 Contrast of synthesized and actual noise of 5#

以加速度响应和本文引入的位移差ΔX（w）作为输入振源时，1#和5#设备的路径到目标点的合成噪声与设备单独开启时船外目标点噪声的对比如图3和4所示。可以看出：以加速度作为振源时，由于受到了其他振源的交叉耦合作用，TMM合成结果与实际计算结果吻合较差。路径5在一个独立的舱内，其受到其他振源的耦合较弱，结果误差较小。而路径1受其他路径的耦合作用较强，导致其误差更大。由于低频段各振源之间的交叉耦合性较强，图中低频时的结果要劣于高频时的结果。图中以ΔX（w）作为输入振源可以在一定程度上避免振源间交叉耦合作用的影响，基于此振源的目标点噪声合成值与实测结果吻合较好，除个别频率点外，误差均不超过3dB。以整个频段的总声压级为基本量，5条传递路径对目标点噪声的总贡献量排序分别为2#＞1#＞3#＞5#＞4#，此结果与分布运转法得到的结果完全一致，证明了本文TMM在船舶机械设备噪声源识别和贡献量分析中的有效性。

3 实船海上振动－声辐射试验及数据分析

为了进一步验证TMM在实船机械设备噪声源识别中的有效性，本文进行了实船锚泊状态下的振动－声辐射试验，试验在水域宽阔的海上进行，背景噪声满足测试要求，试验主要分析低频段特性，主要测试的振动噪声源为设备1、设备2、设备3。试验首先采用便携式振动设备在船内进行设备振动情况的预评价，为振源识别提供测点选取的基础数据，然后在每个设备选择2个典型的机脚，在每个机脚的隔振器两端即设备和基座上分别各布置1个三向加速度传感器，布置在紧挨机脚并尽量避免将测点布置在振型的节点处。试验中共布置三向加速度计12个，在船外部指定水域指向性较大的方向布放3枚水听器采集声场数据，水听器布放深度与设备所在位置基本保持同一水平面。试验典型设备与传感器示意图如图5所示。

图5 典型设备与传感器图Fig．5 Typical equipment and sensors

试验中船外的辐射噪声与船体的结构振动数据实现了同时基采集，并对声场信号进行了时延的修正。为有效地实现TMM，各设备在不同的转速或负载的条件下工作，尽可能多的变化设备的工况组合，共测得了15组不同工况的组合，每组工况采样6次。并对3台设备分别单独开启，用以验证TMM结果是否正确。

3．1 船外噪声合成与验证

使用便捷设备对各机脚的振动情况进行预评价，得出同一设备的各机脚间的振动相关性较强。因此，进行噪声源识别时取每个设备一个机脚处的测点（为保证信噪比，优选振动响应较大的测点作为振源）。由于本文所选低频段内的测试数据相干性较好，且该频段受其他因素的干扰也相对较小，所以将隔振器与机械设备、基座接合部位按点接触处理。考虑x，y，z向的振动传递即每个设备3个路径点，总路径点数m＝9。通过TMM程序对3个振源（9个路径点）到船外目标点声压贡献量进行合成，并与实测结果相比（选取一个信噪比较高的水听器作为目标点），结果见图6。可以看出，船外目标点的合成声与实测噪声的频谱频域分布基本一致，主要峰值频率均能一一对应，且对应幅值吻合较好。通过TTLS修正的结果要优于LS修正的结果，即TTLS可以有效地缓解振动输入矩阵ΔX在求逆过程中的不适定问题，有效地避免了振动加速度和声压响应的测量噪声引起传递函数矩阵估计的不稳定。

图6 噪声实测值和合成值比较Fig．6 Contrast of synthesized and actual noise

图7为设备3在不同形式输入振源条件下，船外目标点的噪声合成值与实测值的比较图。图中以振动加速度作为振源时，因振源间存在耦合效应，计算误差普遍偏大，在0．05～0．6的低频段内尤为明显。在频率点0．2和0．65左右出现了较大的误差，分析认为：可能由于设备1振动耦合所致。而以输入位移之差ΔX（w）作为输入振源时，可有效地减轻各路径点间交叉耦合作用的影响，其主要峰值频率点处噪声合成值与实测值吻合较好，进一步证明了TMM方法的有效性。

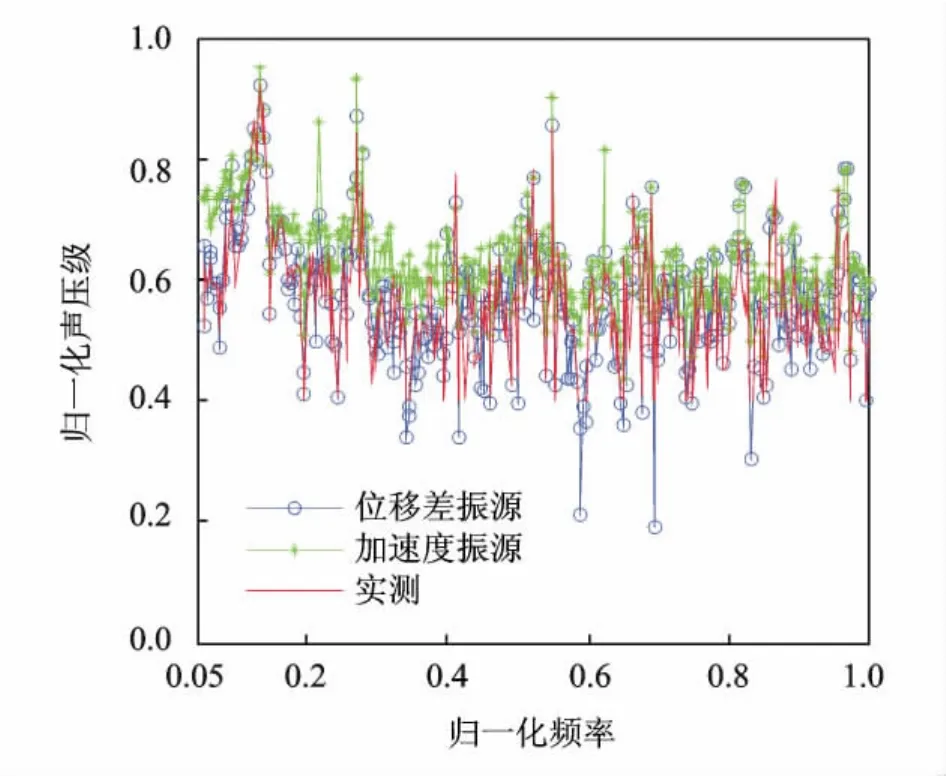
图7 设备3合成和实测噪声对比图Fig．7 Contrast of synthesized and actual noise of 3#

3．2 噪声贡献量分析

为分析3个设备9条路径对目标点的贡献量，给出噪声贡献频谱云图如图8所示。图中显示，y1，y2和z3路径在整个频段内具有较大贡献，在0．15频率点附近目标点的噪声总合成较大，此处各路径的贡献量排序为z3＞y2＞y1＞z2＞x2＞x1＞x3＞y3＞z1。以频点0．05到1整个频带内的声压级为基本量，得到各路径的对目标点的噪声贡献量排序为z3＞y1＞x3＞z2＞x1＞z1＞y3＞x2＞y2，由此得出3个设备的总贡献量排序为设备3＞设备2＞设备1，该结果与某设备单开的实测结果完全一致。可见，TMM方法在噪声贡献量排序分析中具有较高的可靠性，且可对关心的单个频率点或频带进行针对性的分析，适用性更强。

图8 噪声频谱云图Fig．8 Cloud map of noise frequency spectrum

利用噪声的贡献谱图分析时，值得注意的是，一条具体的传递路径所传递的能量引起的声压贡献与幅值和相位相关，如图8中存在某些频率点处各路径均有较大的贡献，但是总的贡献量依然很小，这可能是由于不同路径之间的相位反向，使得总的贡献量降低。因此，在进行传递路径分析时，先弄清楚各路径所传递噪声的相位是特别重要的。

由图9贡献量的极坐标图可分析各传递路径的幅值和相位对目标点声压响应的影响，图中以目标点总合成噪声的相位116．6°为基准相位，即图中x向。可见，传递路径矢量和x向夹角越小对总合成的影响越大，当与x向同向时，增加目标点的噪声总合成值；反之，抵消了总合成的噪声值。在进行噪声源及其传播路径的识别和控制时，要特别注意与x向夹角小且幅值大的传递路径，如图中传递路径z1，y2，z2，x2，y3，z3对目标点的噪声响应起增强效果，传递路径x1，y1，x3对目标点的噪声响应起削弱效果。综上，在机械噪声源识别和贡献量排序时，考虑各传递路径的幅值和相位的影响更符合实际情况，且更有利于减振降噪措施的正确实施。

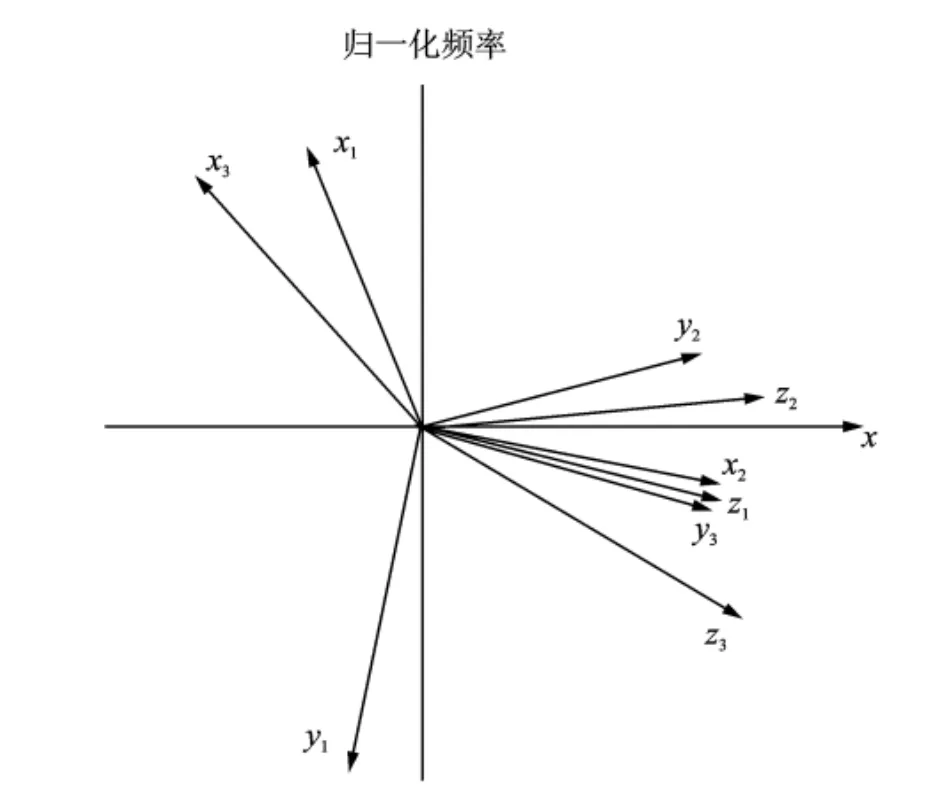
图9 各路径贡献的矢量图Fig．9 Vector superposition of each transfer path

4 结 论

传递率矩阵方法（TMM）在船舶噪声源识别中具有快速、理论简单和真实反映设备运行特性等优点，这些优点都是传统方法难以比拟的。但在实际工程应用中该方法仍存在缺陷，文章全面分析了这些缺陷并提出解决方案，重点解决了振源间存在交叉耦合的缺陷。基于TPA理论提出一种新的基于传递率矩阵方法（TMM）的噪声传递路径分析模型，通过船舶水中振动－声辐射仿真分析和实船海上振动－声辐射试验对新模型进行验证。结果显示，该模型有效地避免了输入振源之间的交叉耦合，能够高效、准确地进行船舶噪声源识别和贡献量分析，进而指导船舶的声学设计和噪声预报，同时为船舶的振动噪声治理提供有效的依据。

［1］ 杨德森．水下航行器噪声分析及主要噪声源识别［D］．哈尔滨：哈尔滨工程大学，1998．

YANG Desen．Noise sources identification and analysis for underwater vehicles［D］．Harbin：Harbin Enginerring University，1988．

［2］ 章林柯，何琳，朱石坚．潜艇主要噪声源识别方法研究［J］．噪声与振动控制，2006，（4）：7—10．

ZHANG Linke，HE Lin，ZHU Shijian．Review on the methods of identification of submarine main noise sources［J］．Noise and Vibration Control，2006，（4）：7—10．

［3］ Knapen P L．Transfer path analysis related to booming，performed on a car［D］．The Netherlands：Eindhoven University of Technology，2006．

［4］ 田雄，李宏成，吕先锋，等．基于传递路径试验分析的变速器敲击噪声优化［J］．振动工程学报，2010，23（6）：642—648．

TIAN Xiong，LI Hongcheng，LU Xianfeng，et al．A study on transmission rattle noise optimization based on transfer path test analysis［J］．Journal of Vibration Engineering，2010，23（6）：642—648．

［5］ Noumura K，Yoshida J．Method of transfer path analysis for interior vehicle sound by actual measurement data［A］．Proceedings of JSAE Annual Congress［C］．Yokohama，Japan，2006：7—12．

［6］ Klerk D D，Ossipov A．Operational transfer path analysis：Theory，guidelines and tire noise application［J］．Mechanical Systems and Signal Processing，2010，（24）：1 950—1 962．

［7］ Gajdatsy P，Janssens K，Desmet W，et al．Application of the transmissibility concept in transfer path analysis［J］．Mechanical Systems and Signal Processing，2010，（24）：1 963—1 976．

［8］ 原春晖．机械设备振动源特性测试方法研究［D］．武汉：华中科技大学，2006．

YUAN Chunhui．A study on the test approaches of characterization of machinery as vibrational sources［D］．Wuhan：Huazhong University of Science and Technology，2006．

［9］ Diana M S，Sabine V H．Level choice in truncated total least squares［J］．Computational Statistics and Data Analysis，2007，52：1 103—1 118．

［10］Qiu Y，Griffin M J．Transmission of vibration to the backrest of a car seat evaluated with multi－input models［J］．Journal of Sound and Vibration，2004，274：297—321．