小波相关排列熵和HMM 在故障预测中的应用＊

冯辅周，司爱威，江鹏程

（装甲兵工程学院机械工程系，北京 100072）

引 言

机械系统的大部分故障都不是瞬时发生的，而是渐进性的，其故障演变往往经历发生、发展直至恶化的过程，而且有征兆可寻。统计表明装备机械系统的大部分故障是具有时间依存性的、可预知的趋势性故障，采用科学有效的故障预测方法往往能够揭示故障的发展变化，有利于避免设备恶性事故和继发性事故的发生。

故障预测包括3个重要环节：特征提取、退化状态识别和剩余寿命或故障概率预测。其中，特征提取是故障预测的关键技术，直接关系到退化状态识别的准确性和故障预测的精度。然而，在故障发生前系统发展变化的特征信息是一种早期故障信息，其具有的弱信息特征导致信噪比较低，在故障预测中有用信息往往被复杂系统的时变、非线性运行特征、工况和负载变化、环境干扰和测试系统噪声等非故障信息所淹没，如何从强噪声背景中提取微弱特征信号，是该领域研究的一个热点和难点。

目前，对于微弱信号的检测还没有一种特别有效的方法。自从Donoho等提出了小波阈值去噪方法后［1］，小波分析便广泛应用于微弱信号检测，但在实际应用中效果并非十分理想。而且Donoho提出的硬阈值和软阈值方法中均有一定的缺陷：在硬阈值方法中，由于阈值函数在所取的阈值处不连续，用该方法得到的小波系数对信号进行重构时会引起波动；由软阈值方法得到的小波系数虽然连续，但这些系数与实际信号经小波分析得到的系数存在误差，这就直接影响着重构信号与真实信号的逼近程度。有学者利用小波多分辨率分析的特点［2，3］，对微弱信号进行处理，在强背景噪声下显现并增强信号的目标特性，提高信噪比。但当信号非常微弱时，信号经小波分析处理后，有用信号分量的功率仍然小于噪声信号分量功率，甚至有可能仍然相当微弱，比噪声小几个数量级甚至被噪声淹没，或者在某些特定场合下噪声特性与白噪声特性不符合，使得利用小波变换降噪受到限制。同时，当噪声频率与信号频率接近或重合时，抑制噪声的同时，有用信号往往也不可避免地受到损害，这极大影响了微弱信号的检测。

针对这一问题，本文基于小波熵理论的基本思想，引入滤波效果良好的小波相关滤波法和对信号微弱变化特征敏感的排列熵算法，定义了一种新的小波熵概念——小波相关排列熵（wavelet correlation permutation entropy，WCPE），进而提出了一种基于小波相关排列熵的特征提取新方法。试验表明，该方法能有效地表征轴承早期故障特征。

另外，传统的故障预测方法停留在静态观测的基础上，仅取某一时刻的特征信息进行比较分析，这往往忽视了故障发生前后的关联信息，没有揭示系统潜在状态所发生的变化特征，因而也难于对故障的发生和发展做出准确预测。

隐马 尔 可 夫 模 型 （Hidden Markov Model，HMM）是一种动态模式识别工具，适用于动态过程时间序列建模并具有较强的时序模式分类能力，而且特别适用于非平稳、重复再现性不佳的信号分析。本文引入HMM，结合基于小波相关排列熵的特征提取方法，探讨其应用于机械系统故障预测的技术和方法。试验结果表明该方法能有效地识别系统的退化状态，并能准确地预测故障发生的概率。

1 小波相关排列熵特征提取方法

1．1 小波相关滤波法原理

小波相关滤波法降噪的基本思想是基于小波分解后相邻层系数的相关性，相邻分解层的小波系数直接相乘后，突变信号分量会得到增强，而噪声信号分量变得更加微弱，利用阈值检验，从噪声中检出重要的信号边缘，并移除噪声，使得信号的信噪比大大提高［4，5］。小波相关滤波方法具有容易实现和鲁棒性好等特点，可以应用于在线监测与诊断系统进行实时信息处理。

直接将信号小波变换系数值在几个分解层次上进行相关运算（记为Cl（m，n）），可以相当准确地确定信号边缘或其他重要特征的位置。

式中W表示信号的小波变换，m表示分解层数，N表示离散信号的点数，n表示时间，l表示直接相乘所包含的层数。若M表示总的分解层数，则应该有m＜M－l＋1。当某个局部存在信号边缘或其他重要特征时，这种方法可以将背景噪声除去。直接将信号数据进行尺度空间相关，将锐化和增强信号的主要边缘，同时噪声和次要边缘将被压缩。小波相关滤波法的具体计算过程可参考文献［6］。

1．2 排列熵理论

排列熵（Permutation Entropy，PE）是近年来新兴的一门研究自然界中的不规则性以及非线性系统的算法，它可以将以前不能定量描述或是很难定量描述的复杂系统用一种较为简便的方法描述出来。排列熵反映了一维时间序列复杂度，对信号变化具有较高的敏感性，可以很好地放大系统的微变信号，同时检测出复杂系统的动力学突变［7］。由于系统设备在即将发生异常或故障时，其非线性因素的影响是不同的，所表现的信号复杂性也会不一样。因此，利用排列熵进行早期故障诊断是可行的。

排列熵的大小表示时间序列｛X（i），i＝1，2，…，n｝的随机程度：排列熵的值越小，说明时间序列越规则，反之，则时间序列越接近随机。排列熵的变化反映并放大了时间序列的微小细节变化。排列熵的具体计算方法可参考文献［8］。

1．3 小波相关排列熵原理

当机械系统发生早期故障时，故障信息微弱，信噪比较低，直接进行小波分解无法提取出微弱的故障信息。小波相关滤波法不仅可以对目标信号有效降噪，而且不会有分辨率的损失。因此，采用小波相关滤波法可以提取信号微弱的故障特征信息，得到信噪比较高的各层重构信号。基于上述小波熵理论和对突变信号变化敏感的排列熵算法，对小波相关滤波处理后的各频段重构信号进行排列熵分析，即可得到各频段信号的排列熵复杂度，由此来识别机械系统的运行状态。

信号x（n）经过小波相关滤波降噪处理后，得到各分解层次下较高信噪比的高频系数：Dj｛dj（k），k＝1，2，…，N，j＝1，2，…M｝和低频系数C，它们分别包含了信号从高频到低频不同频带的信息，体现了不同分解层次下局部特征的直观估计。为了定量描述各频段小波系数所包含的故障特征信息，还需从得到的各层小波系数中提取反映设备运行状态的特征参数，有利于系统运行状态的分析和识别。在此可以把小波相关滤波降噪处理后的得到的各层小波系数Dj（j＝1，2，…，m，m＋1）看成对信号x（n）的一种划分，定义这种划分的测度为

式中dF（j）（k）为dj（k）的傅里叶变换。

借鉴小波熵的基本思想，定义小波相关排列熵为：将pj（k）进行相空间重构，按上述排列熵算法，依次求取经小波相关滤波后各层的排列熵值。

1．4 小波相关排列熵特征提取步骤

根据上述小波排列熵的计算方法，结合振动信号特征提取的实际需求，可总结基于小波相关排列熵的特征提取步骤如图1所示。

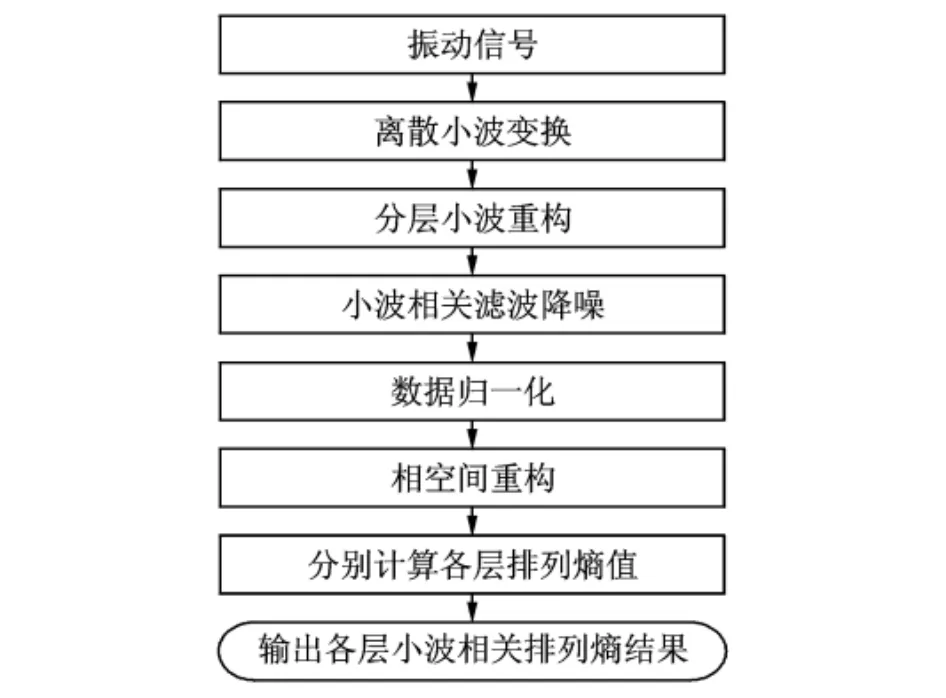
图1 小波相关排列熵特征提取步骤Fig．1 Feature extraction approach of WCPE

首先是对信号进行m层离散小波分解，得到各层的小波系数Dj＝｛dj（k），j＝1，2，…，m，m＋1｝，并对各层小波系数分层进行重构；然后，利用小波相关滤波法对各层小波重构后的信号进行逐层降噪处理，得到信噪比较高的各层分量；之后，在依据式（2）对降噪后的各层分量进行归一化处理的基础上，选取合适的嵌入维数和延迟时间，对其进行分层相空间重构，得到各层分量的相空间矩阵；最后，依据排列熵算法计算出各层分量的小波相关排列熵值Wp为

2 HMM的基本理论和算法改进

HMM是一个双重随机过程，不仅状态之间的转移是随机的，而且每个状态的观测符号也是随机的。模型中真实的状态是“隐藏的”，不能直接观测，只能通过观测矢量感知它的存在。机械系统故障演化过程通常经历正常、性能下降、故障、失效等几个健康状态衰退阶段，这些健康状态衰退过程在实际中一般不能直接观察到，能观测到的只是系统表现出来的性能或状态征兆，即系统故障衰退健康状态要通过其表现来感知，这和HMM在本质上是相通的。而且HMM可以较好地描述隐藏状态与观测状态间的关联关系。HMM可表示为

式中λ为初始概率分布矢量，A为状态转移概率矩阵，B为观察值概率矩阵。图2可以清晰地表示出一个左右型HMM的基本结构。

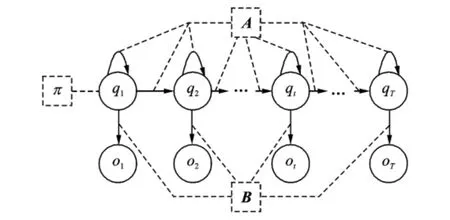
图2 左右型HMM拓扑结构图Fig．2 Framework chart of right－and－left HMM

图2中第1行圆圈表示观测不到的隐状态；第2行圆圈表示可观测到的观测变量。其中π，A和B为 HMM 的3个基本参数，｛o1，o2，…，oT｝为观测序列，它由状态序列｛q1，q2，…，qT｝按观测矩阵B产生；｛q1，q2，…，qT｝被称为状态路径，其各状态间的依赖关系是由转移矩阵A决定。模型中的初始向量π决定初始时刻系统所处的状态。

针对HMM的概率计算、最优状态序列选择和模型训练（参数估计）等3个问题，通常对应有前向后向算法、Viterbi算法和Baum－Welch算法来解决［9］。而参数估计在HMM的应用中占有举足轻重的地位。传统的Baum－Welch算法（BW）虽然可以确保似然值单调上升，且该算法具有收敛性，但是该算法存在收敛速度较慢，数值运算困难等缺点，而且容易陷入局部最优。因此寻求更好的参数估计方法具有十分重要的意义。本文从优化角度出发，将遗传算法引入HMM的参数估计中。

HMM的参数估计就是根据极大似然准则寻找合适的模型参数λ，使得输出概率P（O｜λ）取得最大值，该过程中还存在约束条件

因而，最大化P（O｜λ）其实就是一个带有约束的优化问题，基于此，本文采用基于惩罚策略的遗传算法来处理这个问题。首先，定义一个模型参数λ违反约束程度的量

式中M1和M2为极大正数。

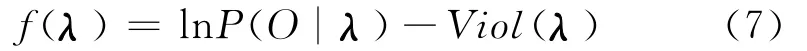
然后，可以确定适应度函数为然后即可运用遗传算法进行HMM参数估计。

3 故障预测模型的建立

基于以上的分析，本文建立了基于HMM的预测模型框架，如图3所示。

整个预测流程为：首先提取历史观测数据的特征信息输入HMM模型，并用HMM的参数估计方法分别训练各个退化状态识别模型以及全寿命模型，然后就可以提取当前观测数据的特征信息并输入到训练好的各个退化状态识别模型，根据最大似然概率值即可判断当前观测数据代表的退化状态，同时结合全寿命状态转移概率矩阵即可计算当前退化状态下故障发生的概率。

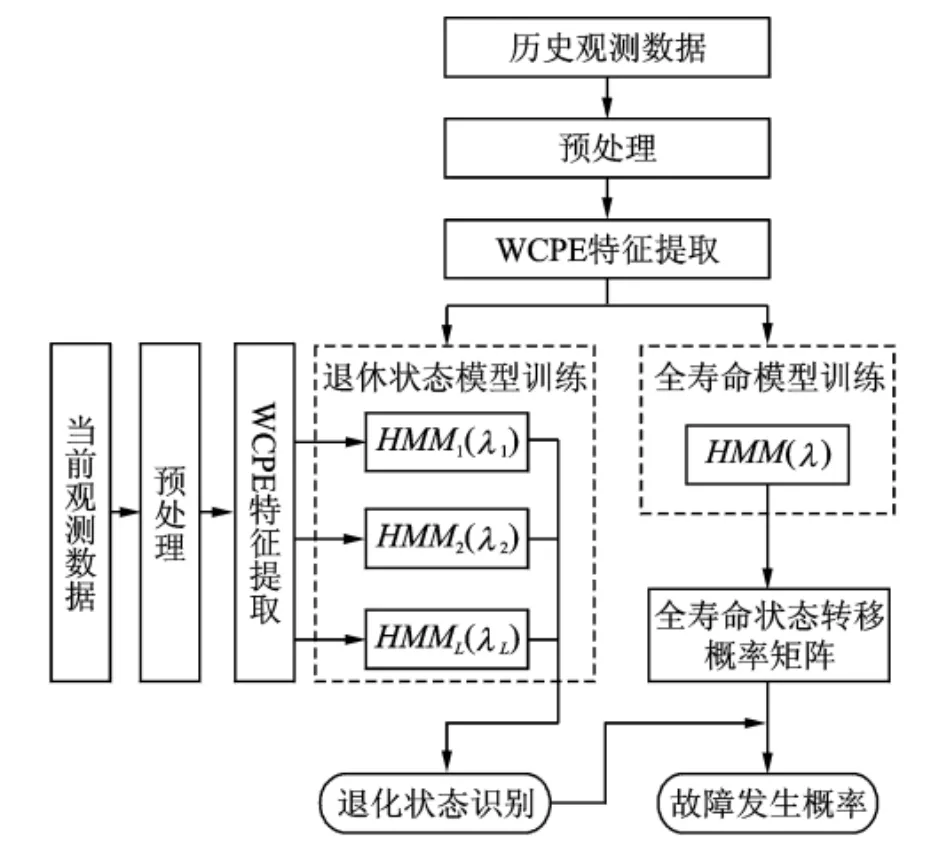
图3 基于WCPE和HMM的预测模型框架Fig．3 Framework of prognostic model based on WCPE and HMM

4 实例分析

4．1 数据来源及分析

为验证该方法的有效性，选取来自美国NSFI／UCR智能维护系统中心（IMS）的轴承振动数据进行分析［10］。试验时，在一个轴上安装了4个轴承，轴的转速固定在 2 000r／min，6 000 1b（约等于26 671N）径向载荷用弹性系统加载在轴和轴承上，每个轴承上安装2个美国PCB公司生产的353B33型高灵敏度ICP加速度传感器（一个水平方向，一个垂直方向）。

本文的数据采用了该试验的第2次的测试数据，其采样频率为20kHz，每个文件包含20 480个数据点，每10min记录一个文件，该次试验共采集了984个文件，即试验持续了164h）。试验结束之后，发现轴承1发生外圈磨损失效，这说明该试验记录了轴承1的全寿命数据。图4示出了轴承1垂直方向传感器采集的各文件数据的均方根值Xrms的趋势图。

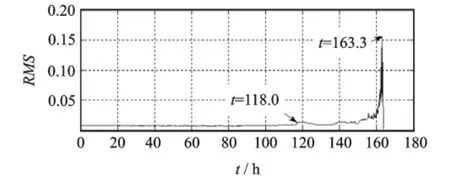
图4 轴承1垂直方向振动信号均方根值趋势图Fig．4 RMStrend chart of bearing 1vibration signal on vertical direction along the time

从图4可以看出，在118．0h之前，轴承1运行比较平稳；当轴承1运行至118．0h时，其振动信号出现微小的跳变，说明轴承已经开始出现异常；118．0～160．0h，振动信号在上下波动，但波动幅度不大，说明轴承在带故障运行，但故障不太严重；当轴承1运行超过160．0h，其振动信号出现剧烈变化，并在163．3h其均值达到最大值，此时轴承已出现严重故障，达到其寿命极限。

另外，从图4可以看出，基于振动信号特征值的趋势分析虽然能够大致反映轴承运行的全寿命过程，但其发生早期轻微故障时（118．0～160．0h），信号反映的特征非常微弱；而且如果在实际应用的复杂机械系统中，特征信号更容易淹没在各种噪声的干扰之中，这就导致在故障发生的早期，检测和发现故障非常困难；而当特征信号表现明显（超过160．0 h）被发现的时候，故障已相当严重，而且此时留给维护人员做出维修决策的时间又非常短暂，往往会导致设备被迫停车或严重损坏的后果，损失将不可估量。

4．2 特征提取

为验证小波相关排列熵特征提取算法在早期故障诊断中的有效性，用该算法对上述轴承原始振动数据进行分析。对每个文件的数据按照基于小波相关排列熵的特征提取步骤依次求取其小波相关排列熵值，其中小波分解层数为4层，由于Daubechies系列小波正交、紧支，对不规则信号较为敏感，同时依据文献［11］的方法选用db4小波基函数进行小波分解。排列熵计算时分别利用互信息法和伪近邻法选取嵌入维数为d＝5［12］，延迟时间为τ＝4。同时，为减少计算量，计算每个文件数据各层的排列熵时，将总长为20 480的数据分为20段，每段1 024点分别求其排列熵值，然后求这20个排列熵值的均值作为该文件数据该层的排列熵。图5示出了轴承1振动信号第一层小波相关排列熵的变化趋势图。

图5 轴承1振动信号第一层小波相关排列熵的趋势图Fig．5 The first layer WCPE trend chart of bearing 1vibration signal along the time

从图5中可以看出：当轴承运行至86．8h，第一层小波相关排列熵值开始跳变，而且变化幅度较大，趋势明显，即振动信号的小波相关排列熵可以检测出轴承的早期故障，而且其检出时间比用均方根值特征检测提前了31．2h。同时也表明了小波相关排列熵算法对微弱信号特征提取的有效性。

为了进行比较，这里直接选取轴承1垂直方向振动信号进行排列熵分析，其中数据分段方法与前文相同。轴承1时域振动信号的排列熵分析结果如图6所示。

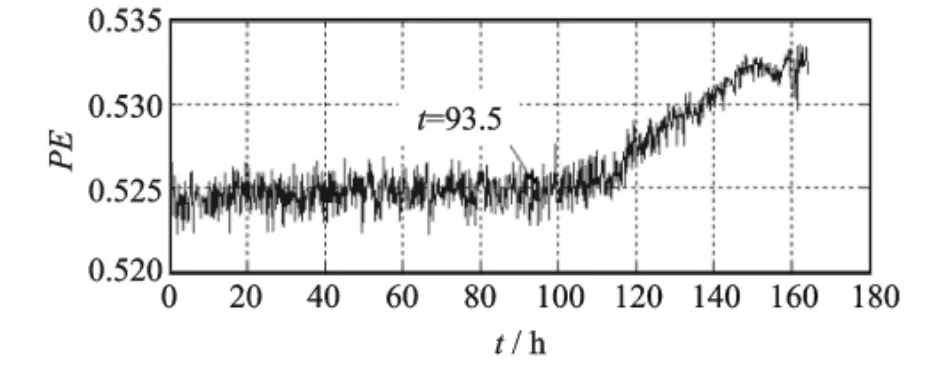
图6 轴承1振动信号的排列熵趋势图Fig．6 PE trend chart of bearing 1vibration signal along the time

从图6中可以看出，时域信号的排列熵特征值也能反映滚动轴承运行的全寿命过程，但对比图5和6，可以明显看出，经这两种算法提取的特征向量检测出轴承状态开始变化的时间是不同的，即小波相关排列熵算法提取的特征向量较早地检测到了轴承的早期故障，而且比排列熵算法提前了6．7h。值得说明的是，该轴承振动数据是在大载荷、高转速的加速寿命试验的条件下采集的，如果是在实际正常条件下运行，提前的时间将会更长。

4．3 退化状态模型训练及识别

为实现轴承的退化状态识别并最终实现故障预测，就要分别建立各退化状态的HMM以及整个全寿命数据的HMM，根据文献［13］算法的分析，该轴承振动数据的最佳退化状态数为6（其中包含1个正常状态、4个退化状态和1个故障状态）。因此，确定训练退化状态模型数为6个，分别为HMM1（λ1），HMM2（λ2），…，HMM6（λ6）。

选用上一节提取的轴承振动数据的小波相关排列熵作为特征信息点进行退化状态的识别和故障预测。从图4可以看出，当轴承运行超过120h（720个文件记录）时，已处于严重故障状态，因此这里仅选取前120h的特征信息作为模型训练和检测的依据。将720个小波相关排列熵特征点划分为120个样本（每小时一个样本），每个样本6个特征点，即观测值数为6。其中，前1～80样本为正常状态的80个样本，81～88为退化状态1的8个样本，89～96为退化状态2的8个样本，97～104为退化状态3的8个样本，105～112为退化状态4的8个样本，113～120为故障状态的8个样本。同时，选取每个状态前一半样本作为训练样本，后一半作为测试样本。

HMM的一个重要参数就是马尔可夫链的状态数，它描述了状态的转移，直接影响模型的性能。本文选取ADC准则来确定各退化状态HMM的马尔可夫链的状态数。通过计算，最佳状态数为5（详细可参考文献［14］）。因此采用5状态HMM初始化模型。因初始状态转移矩阵和初始观测值概率矩阵对离散HMM训练影响较小，这里采用等概率方式产生。分别采用BW算法和GA算法对各退化状态模型进行训练，同时设定训练过程中最大迭代步数和进化代数为100。用遗传算法训练时，种群大小设为40，最大进化代数设为100，交叉概率设为0．8，变异概率设为0．02。图7示出了分别用BW算法和GA算法训练正常状态模型时，各自的相对误差随迭代次数（进化代数）变化的趋势图。

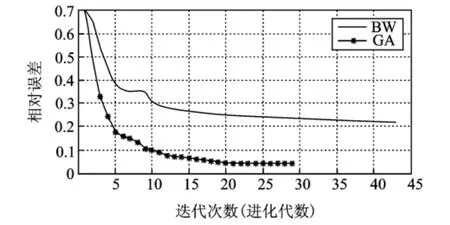
图7 BW算法和GA算法训练误差变化趋势图Fig．7 Training error trend chart of BW and GA

从图7可以看出，使用GA算法训练时的误差曲线明显比使用GA算法训练时的误差曲线平滑，而且BW算法的训练误差曲线存在明显的“平坦区”，这说明BW算法更容易陷入局部最优。同时使用GA算法训练模型时，进化代数达到29时即可收敛，而BW算法需要43步，即GA算法具有更好的收敛速度。另外，使用GA算法收敛时的相对误差要远低于使用BW算法收敛时的相对误差，表明GA算法具有更好的估计精度。

在各退化状态HMM模型训练完毕之后，选取测试样本进行退化状态的识别。识别时，同样将每个测试样本分别输入到6个训练好的退化状态模型CHMM1（λ1），CHMM2（λ2），…，CHMM6（λ6）中求其各自的输出概率，输出概率最大的模型所对应的退化状态即代表该测试样本的识别结果。识别结果表明：正常状态、退化状态1～4和故障状态的测试样本识别正确率分别为90%，75%，100%，100%，100%和100%。因此，可计算6个退化状态模型的总体识别率为93．3%，识别效果比较理想。

另外，本文选取了BP神经网络和SVM模型，利用和HMM相同的训练样本和测试样本进行训练和识别，其中BP神经网络的输入层节点数为6，输入层节点数为3，隐含层节点数为13，最大迭代次数为1 000，误差精度为0．001；SVM 模型采用径向基核函数，并选用“1对1”的多类分类算法。结果显示，BP神经网络的识别率正确率为78．3%，而SVM模型的识别率正确率为86．7%。因此，HMM的识别效果明显优于BP神经网络和SVM模型。

4．4 全寿命模型训练及故障预测

因轴承的整个全寿命过程可分为6个运行状态，在此全寿命预测模型将采用6状态HMM进行训练。为保证训练数据的覆盖性和训练效果，按照各退化状态数据交叉组合的原则，通过前文用到的720个小波相关排列熵特征点构建48个训练样本，每个样本包含6个数据点，分别对应6种退化状态。其中，正常状态的480个特征点中每10点选取第1点作为一个训练样本的第一个观测值，退化状态1～4和故障状态分别包含的48个特征点依次选取作为训练样本的第二、第三、第四、第五和第六个观测值。

将48个全寿命样本输入到全寿命模型中，采用GA算法来训练模型，参数设置与退化状态模型训练时相同，当进化代数达到37时，模型收敛。此时得到训练后的全寿命模型的状态转移矩阵A＊为

在退化状态识别和全寿命模型训练完毕的基础上，即可得出所处状态的发生故障的概率。设轴承处于正常状态和退化状态1～4时发生故障的概率分别为P1，P2，P3，P4和P5，则可计算如下

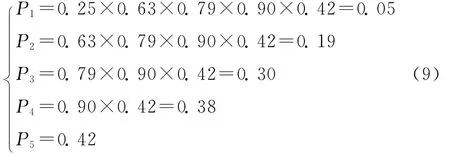
分析式（9）可知，轴承在正常状态发生故障概率较小，而一旦进入退化状态，其故障概率就随之不断增大，这也与机械系统的退化规律相吻合。

在获取处于各退化状态时发生故障概率的基础上，结合新样本退化状态的识别结果，即可得到新样本所处状态发生故障的概率。

5 结 论

（1）轴承振动信号小波相关排列熵特征能有效地表征轴承的运行状态，并较好地检测出轴承故障早期的微弱变化；

（2）基于小波相关排列熵和HMM的故障预测方法能准确地识别机械系统的退化状态，并有效地预测故障发生的概率。

［1］ Donoho D L，Jonnston I M．Adapting to unknown smoothness via wavelet shrinkage［J］．J．Am．Stat．Assoc．，1995，90：1 200—1 224．

［2］ 王仲生，何红，陈钱．小波分析在发动机早期故障识别中的应用研究［J］．西北工业大学学报，2006，24（1）：68—71．

Wang Zhongsheng，He Hong，Chen Qian．Exploring effective early identification of aero－engine rotor faults［J］．Journal of Northwestern Polytechnical University，2006，24（1）：68—71．

［3］ Duan Chendong，He Zhengjia，Jiang Hongkai．New method for weak fault feature extraction based on second generation wavelet transform and its application［J］．Chinese Journal of Mechanical Engineering，2004，17（4）：543—547．

［4］ 杨江天，周培钰．经验模态分解和Laplace小波在机车柴油机齿轮系故障诊断中的应用［J］．机械工程学报，2011，47（7）：109—115．

Yang Jiangtian，Zhou Peiyu．Fault diagnosis for gear train of locomotive diesel engine based on empirical mode decomposition and Laplace wavelet［J］．Chinese Journal of Mechanical Engineering，2011，47（7）：109—115．

［5］ 曾庆虎，邱静，刘冠军．基于小波相关特征尺度熵的HSMM设备退化状态识别与故障预测方法［J］．仪器仪表学报，2008，29（12）：2 559—2 564．

ZENG Qinghu，QIU Jing，LIU Guanjun．Equipment degradation state recognition and fault prognosis method based on wavelet correlation feature scale entropy and HSMM［J］．Chinese Journal of Scientific Instrument，2008，29（12）：2 559—2 564．

［6］ 冯辅周，司爱威，饶国强，等．基于小波相关排列熵的轴承早期故障诊断技术［J］．机械工程学报，2012，48（13）：73—79．

Feng Fuzhou，Si Aiwei，Rao Guoqiang，et al．Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy［J］．Chinese Journal of Mechanical Engineering，2012，48（13）：73—79．

［7］ 刘永斌，龙潜，冯志华，等．一种非平稳、非线性振动信号检测方法的研究［J］．振动与冲击，2007，26（12）：131—134．

Liu Yongbin，Long Qian，Feng Zhihua，et al．Detection method for nonlinear and non－stationary signals［J］．Journal of Vibration and Shock，2007，26（12）：131—134．

［8］ 冯辅周，饶国强，司爱威，等．排列熵算法研究及其在振动信号突变检测中的应用［J］．振动工程学报，2012，25（2）：221—224．

Feng Fuzhou，Rao Guoqiang，Si Aiwei，et al．Research and application of the arithmetic of PE in testing the sudden change of vibration signal［J］．Journal of Vibration Engineering，2012，25（2）：221—224．

［9］ Bunks C，Mccarthy D．Condition－based maintenance of machines using hidden Markov models［J］．Mechanical Systems and Signal Processing，2000，14：597—612．

［10］Qiu Hai，Lee J，Lin Jing，et al．Wavelet filter－based weak signature detection method and its application on roller bearing prognostics［J］．Journal of Sound and Vibration，2006，289：1 066—1 090．

［11］Yang H T，Liao C C．A de－noising scheme for enhancing wavelet－based power quality monitoring systems［J］．IEEE Transactions on Power Delivery，2001，16（3）：353—359．

［12］谢忠玉，张立．相空间重构参数选择方法的研究［J］．中国科技信息，2009，（16）：42—43．

Xie Zhong－yu，Zhang Li．Selection of embedding parameters in phase space reconstruction［J］．China Science and Technology Information，2009，（16）：42—43．

［13］吕克洪．基于时间应力分析的BIT降虚警与故障预测技术研究［D］．长沙：国防科学技术大学，2008．

Lv Kehong．Research on BIT false alarm reducing and fault prediction technologies based on time stress analysis［D］．Changsha：National University of Defense Technology，2008．

［14］舒晓娟，陈洋波，任启伟．模型选择准则在洪水频率分析中的应用［J］．水利学报，2010，41（1）：80—85．

Shu Xiaojuan，Chen Yangbo，Ren Qiwei．Model selection criteria for flood frequency analysis［J］．Journal of Hydraulic Engineering，2010，41（1）：80—85．