航空常用铝合金动态拉伸力学性能探究

王 雷， 李玉龙， 索 涛， 郭亚洲

(西北工业大学航空学院，西安 710072)

铝合金由于具有密度低、比强度高、耐腐蚀性强、易导热导电、塑性和加工性能良好、成本低等一系列优点，一直是飞机机体结构的主要用材。从波音、麦道和空中客车公司大型客机的选材情况［1］来看铝合金已成为飞机主要轻型结构材料。在飞机结构设计中，要充分考虑铝合金部件经常会受到冲击载荷作用这一情况，此类载荷的特点是作用时间非常短，通常以毫秒、微秒的短时间发生运动参量的变化［2］，应变速率非常高。为了提高该类结构在动态情况下的性能和可靠性，首先就需要对这些材料的动态拉伸力学性能有一个充分的了解［3］。过去对铝合金力学性能的研究中［4～10，13］，飞机用铝合金在极端环境下的受载性能成为研究者关注的焦点。Mukai等［4］研究了 IN905XL细晶铝合金的力学性能，结果表明在应变率为10s－1时铝合金表现为负应变率敏感性，当应变率达到103s－1以上时，表现为正应变率敏感性;高应变率下的伸长率普遍大于低应变率下伸长率。Smerd等［5］研究了 AA5754与AA5182两种铝合金在应变率为 10－3～103s－1、温度为23～300℃下的动态拉伸性能，结果表明随着应变率的提高，失效应变增大;温度对失效应变影响不大，但温度越高，流动应力越低，并建立了两种材料的Johnson-Cook本构模型。Oosterkamp等［6］在应变率为0.1 ～ 3000s－1，温度为 20 ～ 515℃ 的条件下对AA6082铝合金进行了动态力学性能测试，在温度为20～340℃条件下对AA7108铝合金进行了同样测试，结果与Smerd基本相符。Peng等［8］研究了3004铝合金在应变率为 5.56 ×10－5～5.56 ×10－3s－1，温度为233～573K条件下的力学行为，得出动态应变时效下的锯齿状流动应力及负的应变率敏感性，并获得一个重要的转变温度Tt，通过微观机理解释了锯齿状流动应力的出现。Shi等［9］研究了 Al-4Y-4Ni与Al-4Y-4Ni-0.9Fe两种细晶铝合金在高温高应变率下的力学性能，结果显示两种铝合金有明显的正应变率敏感性，随着应变率的提高，铝合金拉伸伸长率增大。只是已有的文献中，铝合金在不同应变率下的拉伸失效应变研究中并非重点，另外，不同牌号铝合金的动态本构Cowper-Symonds模型参数也缺乏资料。

本工作选取航空结构件中应用广泛且非常重要的五种铝合金 2A12-CZ，2A12-M，2024-T351，7050-T74和7050-T7451进行试验，利用分离式Hopkinson拉杆设备(SHTB，Split Hopkinson Tension Bar)得到材料的动态拉伸真实应力-应变曲线。在此基础上，分析了这五种航空铝合金动态性能之间的差异。选取Johnson-Cook本构模型、Cowper-Symonds本构模型，拟合得到了它们的动态本构方程。

1 试验

1.1 试验材料

试验材料为2A12铝合金、2024铝合金、7050铝合金，其中2A12铝合金有两种热处理方式CZ和M，2024铝合金有一种热处理方式T351，7050有两种热处理方式T74和T7451。动态拉伸试样标距段尺寸为φ3mm×6mm。准静态拉伸试样标距段尺寸为2mm×20mm×45mm。各牌号铝合金成分如表1所示。

表1 化学成分(质量分数/%)Table 1 Chemical composition of aluminium alloys(mass fraction/%)

1.2 试验设备及试验原理

准静态拉伸试验是在CSS-88000系列电子万能试验机上完成的，试验温度为室温，采用速率控制加载，应变率约为 10－3s－1。

动态拉伸试验是在分离式Hopkinson拉杆设备上完成的。其装置示意图见图1。

图1 Hopkinson拉杆装置示意图Fig.1 The sketch of SHTB device

Hopkinson拉杆系统用于材料动力拉伸力学性能的测试。其装置包括气室、子弹、入射杆，透射杆以及能量吸收装置。拉杆装置的子弹为一个套管，入射杆远离试样一端设计为带凸台的结构，子弹在气室压力作用下以一定速度撞击入射杆凸台，从而在入射杆中产生一列拉伸应力波向试样传播，并对试样施加动态拉伸载荷。由于试样与杆子的波阻抗不同，一部分入射波反射回入射杆中，另一部分经过试样传入透射杆。通过测量入射杆和透射杆上相应的入射、反射和透射应力波，并根据一维应力波理论，可以得到试样的应力和应变信息。利用超动态应变仪通过粘贴在入射杆与投射杆上的应变片来获得脉冲信号，根据一维应力波理论得到应变率、应变、应力分别为［11］:

由于试件的厚度很小，可引入均匀性假设，即:

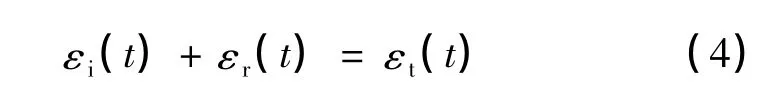
式中:εi(t)为入射应变波，εr(t)为反射应变波，εt(t)为透射应变波，C0为杆弹性波速，A0为试样原始横截面积，l0为试样原始长度，A与E分别是杆的横截面积与弹性模量。若需要材料的真实应力应变曲线，考虑试样截面积的变化，则需对式(2)，(3)进行修正，得到真实应力S与真实应变ψ［12］:

2 试验结果与讨论

2.1 铝合金动态拉伸真实应力应变曲线

五种航空常用铝合金的动态拉伸试验采用西北工业大学冲击动力学试验室的Hopkinson拉杆试验装置。图2所示为试验得到的五种铝合金在不同应变率下的拉伸真实应力应变曲线。

从图2可以看出，室温下，五种铝合金在同应变率的真实应力应变曲线的总体变化规律为:材料经过弹性段后随着应变的增加，应力不断升高，有一定应变硬化效应，接着流变应力呈现比较明显的稳态流变特征，当流动应力达到峰值后，铝合金进入应变软化阶段，随后材料发生破坏。这种情况可以认为是在材料流动应力达到最大时，材料内部已经有一定的损伤，随着应变的不断增加，损伤积累，抵抗应变的能力不断降低，最后材料破坏。

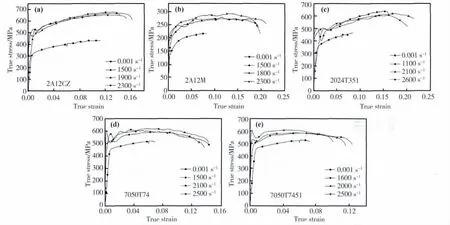
图2 五种航空铝合金拉伸真实应力应变曲线Fig.2 The true tensile stress-strain relationship of five aluminium alloys

2.2 铝合金强度、应变率敏感性

从图2中可以看出，五种铝合金在拉伸过程中，动态抗拉强度明显高于静态抗拉强度，而动态不同应变率之间的抗拉强度相差不大。2A12M铝合金的抗拉强度明显低于其他四种铝合金，动态抗拉强度不到300MPa。7050T74与7050T7451两种铝合金的屈服强度较高，这是由于7050系列铝合金为Al-Zn-Mg-Cu 铝合金，另外还有0.08% ～0.15%Zr［13］，Zr容易与Al形成Al3Zr颗粒，Al3Zr颗粒的存在将对位错运动起钉扎作用，引起屈服应力提高。五种铝合金屈服应力与应变率的关系如图3所示。本工作屈服应力取0.2%残余伸长率时的应力，即 σ0.2。

从试验得到的铝合金应力应变曲线可以看出，应变速率的改变一定程度上影响了材料的强度。这种应变率效应可能是因为较高的应变率不利于材料内部晶粒间滑移传播的连续性，容易在晶界附近引起较大的应力集中，这样会增加变形抗力，最终导致材料的强度随应变率的增高而增大。为定量说明应变速率对铝合金强度的影响，可通过式(7)求出应变速率敏感因子［14］，它表示了当应变率改变时所引起的流动应力的变化。

图3 铝合金在不同应变率下的屈服应力Fig.3 The yield stress of alloys in different strain rate

其中:σ为流动应力;˙ε为应变率。需要说明的是，按照式(7)的定义，m的取值与应变大小有关，本工作中取真实应变为0.07时的流动应力来计算应变率敏感性因子。试验用五种铝合金在拉伸载荷下应变率敏感因子如表2所示。从表2中可以看出，在这五种合金中，2A12CZ应变率敏感性明显强于其余四种铝合金，7050T7451应变率敏感性相对较弱。2A12CZ(CZ代表淬火+自然时效热处理)相对于2A12M(M代表退火热处理)有较高的位错密度，根据式(8)可以得出。

式中，m表示应变率敏感因子，K表示波尔兹曼常数，T表示绝对温度，G为剪切模量，b为柏氏矢量，ρ为位错密度，d为平均晶粒尺寸，ξ表示运动位错在一次激活时扫过的面积的参数，α与η为比例常数。Q.Wei等［15］认为对于粗晶材料，晶粒尺寸不变时，位错密度ρ的增大将会导致其应变率敏感性m的增大，所以2A12CZ有较高的应变率敏感性。

表2 五种铝合金应变率敏感因子Table 2 The strain rate sensitivity parameter of five aluminium alloys

2.3 铝合金拉伸断裂失效应变

图4为五种铝合金的拉伸失效应变，从图4中可以看出，五种铝合金动态拉伸失效应变明显大于静态拉伸失效应变。根据Hart［16］建立的高强度材料不稳定准则:

保证材料均匀变形而不发生局部变形的必要条件是有足够大的应变硬化率［17］。通过拟合五种航空常用铝合金均匀塑性变形阶段的Hollomon公式:

得到它们的应变硬化指数(表3)。

表3 五种铝合金均匀塑性变形阶段的应变硬化指数Table 3 The strain hardening exponent in the region of uniform plastic deformation of five aluminium alloys

从表中可以看出应变硬化指数随着应变率的升高而升高，说明应变率越高，应变硬化能力越强，抵抗不均匀变形的能力就越强。所以高应变率下的断裂失效应变较高。

图4 五种铝合金的拉伸失效应变Fig.4 The tensile failure strain of five aluminium alloys

3 本构方程参数的确定与拟合结果

3.1 J-C本构模型与C-S本构模型

在实际工程应用中，一些基于试验构建的本构模型获得了巨大应用。其中，半经验Johnson-Cook(JC)模型［18］综合反映了大应变、高应变率和高温加载下的金属本构关系。而另一种模型——Cowper-Symonds(CS)模型［19］主要用以动态塑性本构关系。

Johnson-Cook模型表达式为:

在式(11)中，A为屈服应力，n为做功硬化系数，B为幂指数前的系数，C为应变率敏性系数。m为温度敏感性系数，γ表示真实塑性应变，=为应变率的无因次表示式。且的数值取1。

表达式的第一个括号表示对应变的依赖性，确切地说表示流动应力在应变率=1s－1，温度T=Tr时随塑性应变变化的函数关系，第二项和第三项分别表示流动应力对应变率和温度的敏感性。第二个因式表示应力与ln˙ε呈线性关系，这在应变率不是很高时与许多金属的特性相符，式中:

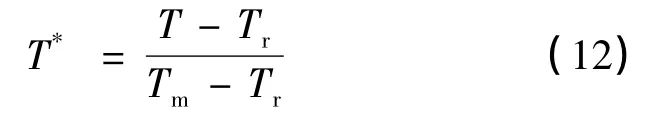
Tr是一个参考温度，取试验温度293K;Tm是材料的熔点温度。考虑到本试验均在相同温度下进行，故参数拟合时不考虑温度项。A，B，n和C是本工作模型待定的四个材料常数。

Cowper-Symonds模型表达式为:

在冲击载荷的作用下，材料的弹塑性应力-应变关系不仅与其本身性质(静态性质)有关，还与加载的时间历程密切相关。因此，材料的塑性本构关系在动态和静态载荷下是有区别的，根据静态试验得到的塑性本构关系不能直接用于动态。而Cowper-Symonds准则就是对静态塑性本构关系进行修正以使其适用于动态的一个理论。在拟合本构中，σD表示动态下的应力，A为屈服应力，B代表幂指数前的系数，n是加工硬化系数，ε为真实应变，˙ε为应变率，D，q是待定的Cowper-Symonds系数。

3.2 本构模型参数的确定

Johnson-Cook模型包含四个材料参数，初始确定可以将模型中各因素对流动应力的影响分别考虑:

(1)对于σ=A+Bγn，A等于材料在˙ε=1 s－1，T=Tr时的初始屈服应力，可以从真实应力应变曲线上直接读取，Bγn是对应力应变曲线强化段的描述，所以只要将强化段的采集点绘制在双对数坐标纸上，便可以通过式(14)确定B和n:

(2)对于1+Cln˙ε*，可直接将此方程作图于半对数坐标纸上，表示截距为1，斜率为C的一条直线，应变率敏感系数C的表达式见式(15)。

(3)Cowper-Symonds模型包含五个材料参数，A，B，n的确定同Johnson-Cook模型。D，q为与材料相关的常数，需要由试验确定［20］。

这种将流动应力各影响因素分开考虑的方法只适用于参数的初值确定，因为它要求确定参数的试验数据必须只包含一项因素的影响，除待定项以外的其他项在试验中取值为1，本试验中所采集的数据包含了应变、应变率和温度的综合影响。模型参数的最终确定是通过比较模型绘制曲线和试验曲线的差异，不断调整参数取值，最终保证模型在试验的温度和应变率范围内与试验结果相符。

3.3 铝合金本构模型参数

根据试验结果，采用Johnson-Cook本构模型和Cowper-Symonds本构模型进行模拟，得到本构参数分别如表4、表5所示。根据参数得到的曲线与试验所得到的曲线吻合程度较好，其中2A12CZ铝合金拟合结果如图5所示，图5a为Johnson-Cook本构模型模拟结果，图5b为Cowper-Symonds本构模型模拟结果。

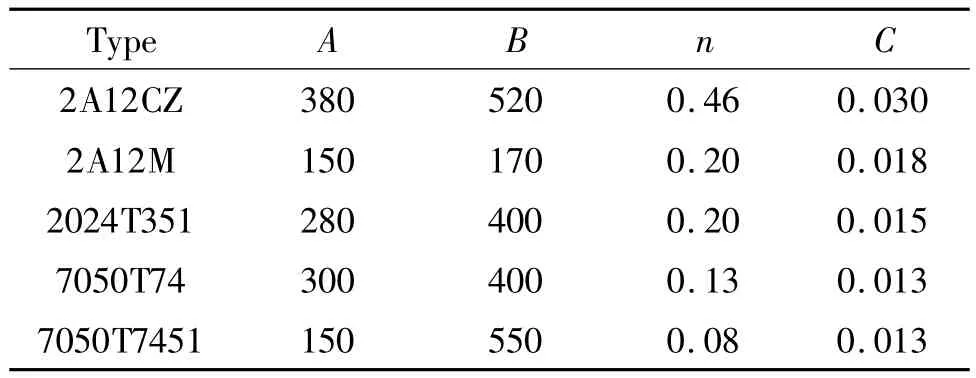
表4 铝合金Johnson-Cook本构模型模拟结果Table 4 The simulation result of Johnson-Cook model

表5 铝合金Cowper-Symonds本构模型模拟结果Table 5 The simulation result of Cowper-Symonds model

图5 Johnson-Cook，Cowper-Symonds本构模拟及与试验数据比较Fig.5 The comparison between experiment figure and simulation of Johnson-Cook，Cowper-Symonds model

4 结论

(1)本试验利用分离式Hopkinson拉杆、电子万能试验机测得了五种航空常用铝合金2A12-CZ，2A12-M，2024-T351，7050-T74，7050-T7451 的动态拉伸、准静态拉伸真实应力应变曲线。

(2)在试验所得数据基础上，分析了这五种铝合金强度、应变率敏感性及拉伸失效应变之间的关系。试验结果显示铝合金动态拉伸强度明显高于静态拉伸强度，2A12M强度在五种铝合金中最低，动态强度不足300MPa。7050系列铝合金的屈服强度较高。五种航空铝合金分别有不同程度的正的应变率敏感效应，其中2A12CZ应变率敏感性最强，7050T7451应变率敏感性最弱，这可以认为是由于材料性质的不同与高应变率下铝合金的变形机制引起的。五种铝合金动态拉伸失效应变明显大于准静态拉伸失效应变。2A12M与2024T351有较高的动态拉伸失效应变，真实应变可达20%以上。

(3)根据试验结果，分析拟合得到了这五种航空铝合金的 Johnson-Cook本构模型、Cowper-Symonds本构模型的拟合参数，可以预测五种铝合金在动态下的流动应力，以方便有限元数值模拟计算。

［1］刘兵，彭超群，王日初，等.大飞机用铝合金的研究现状及展望［J］.中国有色金属学报，2010，20(9):1705－1715.(LIU B，PENG C Q，WANG R C，et al.Recent development and prospects for giant plane aluminum alloys ［J］.The Chinese Journal of Nonferrous Metals，2010，20(9):1705 －1715.)

［2］郭伟国，李玉龙，索涛.应力波基础简明教程［M］.西安:西北工业大学出版社，2006:1.

［3］周培基，霍普金森A K.材料对强冲击载荷的动态响应［M］.北京:科学出版社，1985.

［4］MUKAI T，ISHKAWA K，HIGANGSHI K.Influence of strain rate on the mechanical properties in fine-grained aluminium alloys［J］.Materials Science and Engineering(A)，1995:12－18.

［5］SMERD R，WINKLER S，SALISBURY C，et al.High strain rate tensile testing of automotive aluminium alloy sheet［J］.International Journal of Impact Engineering，2005(32):541－560.

［6］OOSTERKAMP L D，IVANKOVIC A，VENIZELOS G.High strain rate properties of selected aluminium alloys［J］.Materials Science and Engineering(A)，2000:225 －235.

［7］郭伟国，田宏伟.几种典型铝合金应变率敏感性及其塑性流动本构模型［J］.中国有色金属学报，2009，19(1):56－61.(GUO W G，TIAN H W.Stain rate sensitivity and constitutive models of several typical aluminium alloys［J］.The Chinese Journal of Nonferrous Metals，2009，19(1):56 －61.)

［8］PENG K P，CHEN W Z，QIAN K W.Study on dynamic strain aging phenomenon of 3004 aluminum alloy［J］.Materials Science and Engineering(A)，2006，415:53 －58.

［9］SHI X L，MISHRA R S，WATSON T J.Effect of temperature and strain rate on tensile behaviour of ultrafine-grained aluminium alloys［J］.Materials Science and Engineering(A)，2008，494:247 －252.

［10］赵寿根，何著，杨嘉陵.几种航空铝材动态力学性能试验［J］.北京航空航天大学学报，2007，33(8):982－985.(ZHAO S G，HE Z，YANG J L.Experiment investigation of dynamic material property of aluminium alloy［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(8):982 －985.)

［11］王礼立，王永刚.应力波在用SHPB研究材料动态本构特性中的重要作用［J］.爆炸与冲击，2005，25(1):18.(WANG L L，WANG Y G.The important role of stress waves in the study on dynamic constitutive behaviour of materials by SHPB ［J］.Explosion and Shock Waves，2005，25(1):18.)

［12］郑修麟.材料的力学性能［M］.西安:西北工业大学出版社，1999:8.

［13］李娜，李玉龙，郭伟国.3种铝合金材料动态性能及其温度相关性对比研究［J］.航空学报，2008，29(4):903－908.(LI N，LI Y L，GUO W G.Comparison of mechanical properties and their temperature dependencies for three aluminium alloys under dynamic load［J］.Acta Aeronautica，2008，29(4):903 －908.)

［14］陈德民，王刚，孙剑飞，等.高应变速率下钨丝增强锆基块体非晶合金复合材料的变形行为［J］.金属学报，2006，42(9):1003 －1008.(CHEN D M，WANG G，SUN J F，et al.Deformation behaviour of tungsten wires enhanced Zr-based bulk metallic glass composite at high strain rate［J］.Acta Metallurgica Sinica，2006，42(9):1003－1008.

［15］WEI Q M，CHENG S，RAMESH K T，et al.Effect of nanocrystalline and ultrafine grain sizes on the strain rate sensitivity and activation volume:fcc versus bcc metals［J］.Ma-terials Science and Engineering(A)，2004，381(1/2):71－79.

［16］HART E W.Theory of the tensile test［J］.Acta Metallurgica，1967(15):351－355.

［17］SHI X L，MISHRA R S，WATSON T J.Effect of temperature and strain rate on tensile behaviour of ultrafine-grained aluminium alloys［J］.Materials Science and Engineering(A) ，2008，494:247 －252.

［18］JOHNSON G R，COOK W H，A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［M］.Hague:The Netherlands Publishers，1983:541 －547.

［19］LIANG R O，KHAN A S.A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures［J］.International Journal of Plasticity，1999，15:963 －980.

［20］CHEN Z J，YUAN J H，ZHAO Y.Impact experiment study of ship building steel at 450MPa level and constitutive model of Cowper– Symonds［J］.Journal of Ship Mechanics，2007(11):933－ 940.