非战争军事行动装备保障资源运输方式选择模型

杨晓段，李元左，郭瑞平

(装备学院基础系，北京 101416)

装备保障资源运输是非战争军事行动装备保障［1-2］的重要环节。调配方案确定后，如何确保快速、高效地运送保障资源是非战争军事行动装备保障的关键。本文展开对非战争军事行动装备保障资源运输方式的选择与路径优化的模型进行研究。

1 非战争军事行动装备保障资源运输方式选择模型

1.1 问题分析

在道路选择问题上一般可采用单目标规划和多目标规划两种方法，单目标法［3］适用于决策目标只有一个的情况，多目标规划法则适用多个决策目标的情况［4-5］。前面已经分析过影响运输道路选择的因素，可知在实际的非战争军事行动装备保障资源调配中，面对道路选择时要求达到的目标不止一个，如运量要大、运输时效要高、运输安全性要好等目标，所以，对比2种方法，多目标规划方法更为合适建立道路选择模型。

在研究多目标路径选择的实际应用过程中，人们发现使用通常的预测方法所计算出的结果会随着预测区间的推移，误差迅速增大。这主要是由于选择系统自身发展变化的规律是具有时变性的，而常用选择路径的模型方法所用模型往往不是时变的。所以，其选择误差越来越大。人工神经网络理论的发展和应用，为解决上述问题提供了可能。一方面，神经网络具有良好的非线性品质，灵活而有效的学习方式，完全分布式的学习结构，高度并行的处理机制。另一方面，神经网络能够实现非线性映射，使得神经网络具有较好的模式识别能力和在任意精度逼近非线性预测的能力［6-7］。所以，利用人工神经网络方法可以很好地解决非战争军事行动装备保障资源运输方式的选择问题。

1.2 模型建立

下面以一个例子说明多目标的路径选择模型。问题假设:从某仓库运输装备到某部队，有m条路径可以选择，有n个约束目标Vi(i=1，2，…，n)(如运量要求、运输时效限定、运输安全要求等)。要做出道路选择决策，可构造一个n+m个神经元组成的双向联想记忆神经网络，如图1所示。

图1 双向联想记忆神经网络

其中，向量 A 的分量 a1，a2，…，ai，…，an神经元为目标神经元;B 的分量 b1，b2，…，bj，…，bm为决策结果神经元。A、B的每一个分量都属于集合{-1，1}，Wij为两种神经元之间的连接权重。根据联想神经网络理论，用k个决策向量对(A1，B1)、(A2，B2)、…、(Ak，Bk)训练网络，可将 k 种决策模式作为专家的知识或经验联想存储于权矩阵W(W=［Wij］m×n)中。对于任意给定目标A，都可由网络经过叠代而得出联想决策结果B。具体过程如下［8］:

(1)选择训练模式(Ai，Bi)(i=1，2，…，k)，置连接权初始值Wij(0)=0，置˜W为常数(一般为10)以及F=F'=2˜W。

(2)在固定的F和 F'下叠代。根据第 t步的估计值Wij(t)，由下式计算t+1步的估计值Wij(t+1)，同时记录叠代数 n(F，F')。

式(1)中，

(3)如果出现，对进行归一化，算式为

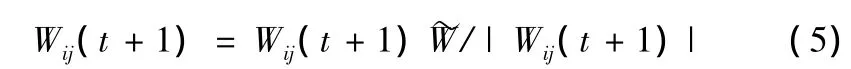
(4)如果叠代次数n(F，F')小于某个预定值(如30)，那么增加F=F+ΔF，F'=F'+ΔF'，其中ΔF=ΔF'=˜W转至步骤(2);否则终止运算。

(5)将k种决策模式作为专家知识和经验联想存储于权矩阵W=［Wij］m×n中。对于给定的目标A，由网络联想得出决策结果B:

初始化，置Aold=A，Bold为任意值。计算B的向量新状态Bnew。

置换Bold、Bnew，有BOold=Bnew。计算A向量新状态Anew:

计算向量A新旧状态差异δ:

若 δ＞0或 δ＜0，令 Aold=Anew，返回(2)继续叠代。若δ=0，网络稳定，结束迭代，得到稳态向量对为(Aold，Bold，此时Aold=A，Bold即为在目标下A的决策结果。

2 非战争军事行动装备保障资源运输路径优化模型

2.1 路径优化模型建立

非战争军事行动中，资源点和储备点的数量并非总是单一，因此在建立路径分析模型时，首先解决任意一个储备点Ri到任意一个需求点Ri之间的路径分析模型。假设由Ri至Ri的交通网络图如图2所示。

图2 Ri至Sj的交通运输网络

在非战争军事行动装备保障资源运输过程中，根据运输环境的变化需要考虑“禁行点”、“必经点”和“必经路段”，“禁行点”就是部队车队不允许通过的地点(如灾害损毁的地段等)，“必经点”就是部队车队必须通过的地点(如装备需求区域、军供站等)，“必经路段”指运输车队必须经过的路段(如任务中的路段、特殊路段等)。

(1)运输网络图分析。图2中圆形、方形、三角形点都为节点，其中方形节点代表“必经点”，三角形节点代表“禁行点”。根据保障资源调度任务建立从起点“Ri”到终点“Sj”的运输网络图记为G=(V，A，B)，其中:V代表节点集(交通枢纽、城镇、军供站、交叉路口或特殊节点等);A代表弧集(路段);B表示路段和节点的广义阻碍强度。

(2)模型基本条件假设。非战争军事行动装备保障资源调配路径优化问题约束因素主要有时间、费用和安全性，而线路里程、行驶速度、交通枢纽和军供站的装卸车、生活保障等都会影响着以上的因素。且在执行非战争军事行动装备保障时各因素因任务实际情况而随时发生改变。因此，需要将求解广义阻碍强度T的多目标问题转化成单目标问题。本章利用线性加权法定义节点和弧的广义阻碍强度:

式(9)中:a为代表弧段长度(当取某一节点时，a=1);t为通过单位长度弧段或节点的时间;s为通过弧段或节点的危险性;Bt，Bh为个目标的权重，且Bt+Bh=1。

在实际计算中，由于各道路具体情况不同，并且各目标值存在一定的模糊性和不同量纲，可依据具体的资源运输方式和任务情况，采用各种方法对各目标进行量化处理，各目标的权重也可用类似的方法确定，从而求出道路的广义阻碍强度。

因为通过运输网络图节点集V中节点的顺序并没有设定，所以非战争军事行动装备保障资源运输不仅必须考虑必经点、禁行点和必经路段，还必须考虑经过节点的顺序问题。即如果要通过某个节点(称为后节点)，则必须先通过它前面的节点(称为前节点)。前面的节点不一定与后面的节点直接相邻，而且前节点和后节点可以是一对一、一对多的关系。对于必经路段，将必经路段的起止节点，作为必经点并提取位于必经路段除起止本节点外的一个点作为必经点，如此，则确定了必经路段跟与其对应的必经节点的一一对应关系。为了使模型充分考虑必经点、禁行点和节点保序问题，建立必经点集合Vk、禁行点集合Vf、前节点集合Va和后节点集合Vb。对于节点Vi(i＞1)∈Vb，则必须存在前节点∈Vf与之对应。其中:Vk⊆V，Vf⊆V，Va⊆V，Vb⊆V。

(3)建立路径优化模型。根据运输网络图G=(V，A，B)，可求解图中由Ri至Sj的最优路径，只需搜索连接Ri至Sj的具有最小阻碍强度B的路径即可。故建立路径优化模型如下:

目标函数为

上述模型中，式(10)为目标函数;式(11)为路径R的整体道路阻碍强度定义;式(12)表示必经点集合一定包含于路径的节点集Vr中;式(13)表示禁行点集合一定不包含在路径的节点集Vr中，但是其包含于V;式(14)表示如果有后节点位于路径上，则至少存在一个对应的前节点也位于路径上，这是保持按顺序经过节点问题;B(i，j)为弧(i，j)的道路阻碍强度;Ar表示路径R中的弧集;Vr表示路径R中的节点集合;Brs表示所求的由Ri到Sj的最优路径。

2.2 遗传算法在运输路径优化中的应用

对于多因素影响下单运输方式的多源多汇路径优化问题，其求解算法很多，其中比较经典的有Dijkstra算法等。用传统的最短路径寻优算法解决存在大规模节点和路径中有必经点和节点保序约束要求的路网时，会出现很多难题。特别是在非战争军事行动装备保障资源调配问题中，由于在实际调配中为了保证调配方案的实施，可能需要多条路径作为预选，因此在求解的结果集中一般要求不仅有最优的路径，还要有次优、再次优的路径等。相比之下，遗传算法(Genetic Algorithms，GA)由于其潜在的并行性和全局寻优及算法构造简单等特点更能求解出多因素影响下单运输方式的多源多汇路径优化模型的理想最优解。

假设基本信息设置如下:需求点信息S，个数m;单个需求点 Sj(j=1，2，…，m);储备点信息R，个数 u;单个储备点Ri(i=1，2，…，u);路径信息 W，路径编号 a:{a1，a2，…，an};节点编号v:{v1，v2，…，vn};路径阻力T。则利用遗传算法，可得出对多源多汇路径优化模型的解法如下。

2.2.1 种群初始化

由于路网中包含了起点、终点和必经点，用字母与整数混合编码方式构造染色体，染色体的基因是网络的节点，而节点的排列顺序代表着起点到终点的路径。设路网G的节点数为N，则染色体的基因数也设定为N。为了解决必经点问题，本文中设计了这样的染色体基因组成方式:第一个为起点“R”;接下来是中间节点，分为两部分，一部分由必经点集合Vk中的全部节点构成，设共有m个节点，另一部份为k个其他节点组成，0≤k≤N-m-2;然后是终点“S”。如果k＜N-m-2，则在“S”点后补“0”，使基因总数保持为 N。这样，染色体中实际的有效基因长度，即从“R”到“S”为m+k+2。通过产生［m+2，N］之间的随机整数来确定染色体的有效基因长度，以及对中间部分基因节点位置做随机排列来得到初始种群中的染色体。由于路径的好坏与基因的排列顺序有关，为了提高遗传算法的收敛性能，在种群初始化时应对染色体做预处理，当检查发现染色体中的两相邻基因生成的无效弧数(没有实际的弧相连)大于该路径总弧数的60%时，则该染色体无效，需重新生成。

2.2.2 节点保序处理

对每个染色体进行节点保序检查，如果有基因点或基因点对没有满足要求，则视情况进行处理。如果需保序的两个基因顺序错误，则可对需保序的两节点互换位置，或直接删除这两个节点(必经点除外)，并在“S”后增加两个“0”基因。如果缺少保序的前节点，则可以删除保序后节点并在“S”后增加一个“0”基因，或当染色体从“R”到“S”的有效基因长度小于N时增加配对的保序前节点并删除“S”后的一个“0”基因。

2.2.3 适应度函数

对于第t代种群中的每一染色体所代表的路径，用式(11)求出其对应的广义权 Wti，其中 i=1，2，…，N，如果染色体中存在没有实际弧相连的基因序列节点对，则其对应的弧权值取一较大数Wmax。为了增加优秀个体繁殖的机会提高算法的性能，建立带有自适应能力的适应度函数:

其中:Wtmin为第t代群中染色体广义权值中的最小者，即最优者。如果染色体适应度函数值越大，则路径越好，反之则越差。

2.2.4 染色体选择

采用改进的轮盘赌选择法。在选择新个体时，首先在当前代的可行个体中选择最佳个体直接进入下一代(若有多个，则随机选取一个)，然后对其他个体采用轮盘赌方式进行选择，如果在当前代中没有可行个体，则全部按轮盘赌方式生成下一代个体。

2.2.5 染色体交叉

由于染色体基因中存在节点保序要求，交叉方式对算法性能有重要影响，因而采用两种交叉方式进行算法性能研究。设有两个父代染色体A(R12546S0)和B(R234156S)，其中节点2与节点4存在“保存关系”，且节点2位于节点4之前，节点5为“必经点”。

(1)部分匹配交叉。(PMX)方式进行染色体的交叉。步骤:从两个父代选择的染色体A，B的基因中随机选择两个交叉点，且必须同时位于两个染色体的“R”点之后，“S”点之前，以保证“R”基因不被交叉。将染色体A，B中的交叉点之间的匹配段互换，得到两个新染色体A1，B1;交叉后，对新染色体进行合法性检查。如果染色体A1(或B1)中出现重复节点，即节点有可能同时出现在匹配段内和匹配段外，则用匹配段内重复节点对应于另一染色体相应位置节点去替换匹配段外的节点，通过反复替换直至染色体中不出现重复节点;进行保序处理。

PMX交叉过程如表1所示。消除重复基因节点，有A2:R341256S0，B2:R254316S，为保持 A2的基因数为 N，删除一个“0”基因，由于其还不符合保序要求，因此可用互换位置法作保序处理后得到新染色体为R321456S。

表1 PMX交叉过程示意

2.2.6 染色体变异

这里采用的染色体变异方式有3种:第1种是在RS节点间随机地删除一个非必经点，同时在“S”后增加一个“0”基因;第2种是当染色体从“R”到“S”的有效基因长度小于N时增加一个基因中没有的节点，并删除一个“0”基因;第3种是互换两个不存在节点保序要求的节点。变异后进行保序处理。在实际操作时，可先分别采用3种方式进行变异，然后取其中适应度值最好者。

3 案例分析

3.1 实例验证

现假设某战区有如图3所示交通网络图。图3中有5个储备点:R1，R2，R3，R4和 R5(分别位于 v1，v20，v30，v3和v5)，3 个需求点:S1，S2和 S3(分别位于 v44，v45和 v48)。

假设单位器材每千米的运输费用见表2。

表2 器材运输费用表

各路段的通过时间、危险性见表3。

图3 某战区交通网络

表3 路段属性表

对以上需求和属性条件进行建模求解如下。

(1)假设从资源点到保障点的每条路径除起止点外至少经过一个“必经点”，而且每个“必经点”至少经过一次。对通过“禁行点”的费用、时间和危险性取较大的常数，比如:f=10000，t=1000，s=10000。

(2)由于非战争军事行动装备保障以时间保障和危险性为主，因此 3 个权重 bf、bt、bs的值分别为0.1、0.6 和0.3。根据遗传算法计算方法，取基因长度48、种群规模200、交叉率0.8、变异率0.05、最大迭代次数为150次，计算得出最优路径。结果如下:

R1至 S1最优路线:v1—v6—v8—v21—v23—v39—v40—v41—v44;R1至 S2最优路线:v1—v6—v8—v21—v23—v39—v43—v45;R1至 S3最优路线:v1—v6—v8—v20—v19—v18—v29—v28—v31—v48;R2至 S1最优路线:v20—v21—v23—v39—v40—v41—v44;R2至 S2最优路线:v20—v21—v23—v39—v43—v45;R2至 S3最优路线:v20—v19—v18—v29—v28—v31—v48;R3至 S1最优路线:v30—v36—v38—v39—v40—v41—v44;R3至 S2最优路线:v30—v35—v45;R3至 S3最优路线:v30—v29—v28—v31—v48;R4至 S1最优路线:v3—v9—v20—v21—v23—v39—v40—v41—v44;R4至 S2最优路线:v3—v9—v20—v21—v23—v39—v43—v45;R4至 S3最优路线:v3—v9—v20—v19—v18—v29—v28—v31—v48;R5至 S1最优路线:v5—v4—v10—v12—v20—v21—v23—v39—v40—v41—v44;R5至 S2最优路线:v5—v16—v29—v28—v29—v30—v35—v45;R5至 S3最优路线:v5—v16—v29—v28—v31—v48。

(3)结果分析与比较。对于本文中的最短路径问题，运筹学中最有效的解法是动态规划法。但是利用动态规划法求解本例中的路径问题时，需要对每段弧线求出广义道路阻碍强度，然后按逐步累积进行计算，这样的计算量随着节点数的增多而急剧增大。特别是在处理“必经点”、“禁行点”、“必经路段”和节点保序问题时，利用动态规划法计算则难上加难。可见，对于求解最佳路径时，遗传算法要比动态规划法更加合理。

4 结束语

根据非战争军事行动特殊需求，提高装备保障快速反应能力，合理选择保障资源运输方式与运输路径，优化装备保障资源配置，在整个非战争军事行动装备保障链中具有关键作用。本文采用神经网络法选择保障资源运输方式，用遗传算法优化保障资源运输路径，并结合实际的交通网络图给出了运输方式选择的案例分析，表明模型的可行性与有效性。

［1］杨晓段，李元左.非战争军事行动装备保障资源储备模型［J］.价值工程，2013，32(4)：19-21.

［2］李元左，杨晓段，郭瑞平.非战争军事行动装备保障资源需求预测模型［J］.价值工程，2013，32(3)：281-282.

［3］施毅，顾毓.基于单目标规划的弹药最佳运输策略分析［J］.武汉理工大学学报：交通科学与工程版，2006(10)：100-102.

［4］张亮，王端民.战时装备保障的多目标运输问题及其求解［J］.物流科技，2009，28(10)：25-27.

［5］余小川.敏捷制造企业供应物流系统的优化研究［D］.重庆：重庆大学，2002.

［6］海金，叶世伟.神经网络原理［M］.北京：机械工业出版社，2004.

［7］焦李成.神经网络的应用与实现［M］.西安：西安电子科技大学出版社，1993.

［8］徐德磊，韩晓龙，梁承姬.基于堆存能力的集卡优化分派研究［J］.武汉理工大学学报，2011(9)：77-81.