神经网络噪声检测的自适应加权均值滤波算法

叶小岭，窦艳艳＋，胡 凯，2

（1.南京信息工程大学 信息与控制学院，江苏 南京210044；2.东南大学 仪器科学与技术学院远程测控技术江苏省重点实验室，江苏 南京210096）

0 引 言

图像在形成、获取和传输的过程中，经常会受到外界噪声的干扰［1］，这不仅导致图像质量下降影响视觉效果，而且严重影响到图像的后续处理工作。依据噪声情况，采取适当的方法有效去除图像中的噪声，对后续的处理过程意义重大［2］。

中值滤波是最常使用的一种滤除图像椒盐噪声的传统方法［3］，在此基础上诸多学者提出了许多改进算法［4－7］，如开关中值滤波 （SMF）、递进开关中值滤波 （PSM）、极值中值滤波 （EM）以及自适应中值滤波 （AMF）等等。但是这些传统的滤波方法在去除椒盐噪声的同时往往会带来图像模糊等问题，对纹理比较细腻的图像以及高噪声密度图像的处理能力不够理想［8－9］。近年来，诸多技术在数字图像处理领域中得到应用。由于神经网络对样本学习后具有联想记忆等特性，因此被广泛地应用于图像处理领域中［10－11］。BP神经网络泛化能力强，结构简单易于实现，适合解决判断图像像素为噪声点还是信号点的分类问题［12］，引入神经网络后图像的滤波性能得到显著的改善［13］。

本文采用训练好的BP神经网络自动对图像中的椒盐噪声进行定位，实验验证了该网络噪声检测性能的准确率高。然后用自适应加权均值滤波方法对检测出的噪声点进行滤除，非噪声点则保持不变直接输出。实验结果表明该算法能够有效滤除图像椒盐噪声并较理想地保护了图像细节。

1 BP神经网络噪声检测模型

本文采用文献 ［14］中的BP神经网络噪声检测算法对噪声点进行定位。首先生成初始棋盘格图作为训练样本，然后将棋盘格图像等分成8部分，对每一部分分别加入不同密度的椒盐噪声，然后用噪声图像与原始图像做差，若差值为0，则将噪声分布矩阵中相应的位置标记为0，反之则标记为1，由此得到图像噪声位置映像，并将其作为神经网络训练的目标图像。将图像像素值、中值、ROAD值［15］作为BP神经网络的输入，采用双隐含层结构，节点数分别为5和3，传递函数采用 ‘tansig’和 ‘purelin’，训练函数采用 ‘trainlm’，最大训练迭代次数在200以内，网络训练允许误差设为0.02。得到的噪声分布矩阵用y表示，其中元素y（i，j）的值为1表示当前像素为噪声点，y（i，j）的值为0表示当前像素为信号点。

2 自适应加权均值滤波

为了在滤波的同时尽可能地保护图像细节，仅对噪声点进行处理，保持信号点灰度值不变。对于噪声点，依据滤波窗口中未被污染的信号点的个数自动调整滤波窗口的大小。图像中各像素间的距离越近，其相关性就越强，所以在赋权值时，对距窗口中心较近的元素赋以较大的值，对距离窗口中心较远的元素，则赋以相对较小一些的权值［5］。

根据噪声点位置对图像进行窗口大小自适应的加权均值滤波，具体步骤为：

（1）设窗口大小为W×W （W 为大于等于3的奇数），初始窗口为3＊3，最大滤波窗口尺寸为WD×WD，根据检测结果，若y（i，j）＝0即非噪声点则不进行处理，按原值输出，否则执行步骤 （2）；

（2）当y （i，j）＝1时，计算出窗口内非噪声点的个数m，若W＜＝WD，执行步骤 （3），否则执行步骤 （4）；

（3）若m≥n （n为正整数），取窗口内所有未被污染信号点灰度值的加权均值L（i＋s，j＋t）作为输出；否则 W ＝W ＋2转步骤 （2）；

（4）若W＞WD，窗口停止扩张，若m≠0，取窗口内所有信号点灰度值的加权均值 L（i＋s，j＋t）作为输出；否则取窗口中所有像素灰度值的均值作为输出。

其中以噪声点 （i，j）为中心的窗口中所有未被污染的信号点的加权计算公式为

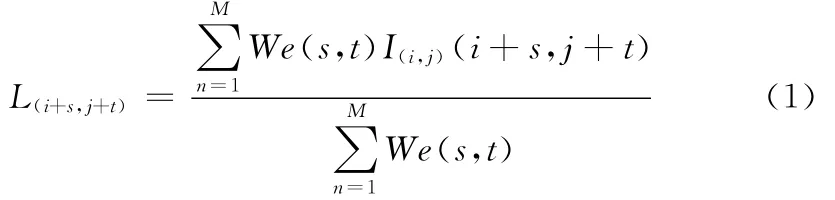
式中：I（i，j）（i＋s，j＋t）——以坐标 （i，j）为中心，窗口中坐标为 （i＋s，j＋t）的未受噪声污染像素的灰度值。We（s，t）表示离中心点 （i，j）坐标偏差为 （s，t）的信号点的权值，计算公式如式 （2）所示，距离中心点越远，所赋权值就越小

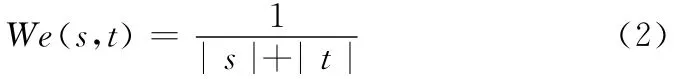
在上述滤波过程中，参数WD和n为人为设定的参数，合理地设置参数WD可以避免当图像被深度污染信号点数比较少时窗口无休止地扩大，可设置为15左右，一般情况下对滤波质量和时间影响不大。参数n的设置对图像质量和时间的影响比较敏感，参数n的取值越大，同等条件下滤波时间越长，n取值为1时滤波时间最短。为了确定同等条件下滤波效果最好的方法所对应的参数n的值，通过对噪声点位置已知的若干幅标准测试图像在不同噪声密度下n取不同自然数 （1，2，3，…）时进行多次实验，实验发现在低噪声密度下n取1、2、3时所对应的滤波算法性能比较相近，滤波质量和时间相差很小，但是在高噪声密度下，尤其是类似图像Baboon这类细节比较细腻纹理比较丰富的图像，n取值为1时所对应的算法的滤波性能相对于n取其它参数时有所下降。实验证明n取值为2时综合效果最好。本文滤波算法中n的取值为2。

3 实验结果与分析

3.1 噪声检测准确性测试

本文滤波方法的思想为先对图像中噪声点进行定位，然后再进行有针对性的滤波，因此噪声检测步骤的准确性是本文滤波方法性能好坏的基础。噪声检测步骤的主要任务为寻找出图像中被椒盐噪声污染的像素位置并进行标记。判断检测性能的主要依据有漏检数和误检数，漏检即某些噪声点没被检测到，误检则为将未被噪声污染的像素检测为噪声点。

本文对多幅标准测试图像分别加入不同密度的椒盐噪声 （10%－90%），接着用训练好的BP神经网络对它们进行噪声检测确定图像中噪声点的位置。测试图像包括Lena（512×512）、Baboon （512×512）、Barbara （512×512）、Boat（512×512）、Peppers （512×512）和 Cameraman（256×256）。将20次试验的均值作为实验结果。噪声性能测试结果见表1。

表1 噪声检测性能测试误检数 （w）、漏检数 （f）

实验结果发现，5幅标准测试图像的漏检数都为0，除了Baboon（512×512）和Peppers（512×512）有误检的像素，其它图像的误检数也都为0。进一步研究发现，Baboon（512×512）可以被检测出一个误检像素，在图像上的位置为 ［512，477］，该像素在原图像和噪声图像中的灰度值都为0。Peppers（512×512）每次检测出来的所有误检像素的灰度值在原图和噪声图像中也都为0。究其原因，这与通常所采用的参考噪声点分布矩阵有关。将噪声图像与原始图像做差运算，若差值为0，参考噪声分布矩阵则标记该点为0，反之则标记该点为1，由此形成了参考的噪声点分布矩阵。所以如果原始图像中某一像素的灰度值为0或255，加入噪声后该像素的灰度值保持不变，则差值为0，参考的噪声点分布矩阵就会把该像素归为信号点这一类，而本文检测算法将该像素归为噪声点这一类，由此产生了误检像素。噪声密度越大，原图中灰度值为0或255的像素分别被白盐点或胡椒点污染的概率就越大，这属于噪声点的范畴，本文算法完全可以检测出来，所以误检数会随着噪声密度的增大而减少。除去上述这种不可避免的误检情况，本文椒盐噪声检测算法可以准确地定位噪声点。

3.2 滤波效果测试

本文所有实验都是基于Pentium （R）4CPU 2.1GHz，内存1G，Win XP，Matlab7.8平台。为了使得到的数据更可靠，避免偶然性造成测试误差，本文所得数据均为20次仿真实验结果的均值。采用峰值信噪比 （PSNR）作为客观评价尺度，峰值信噪比的定义为

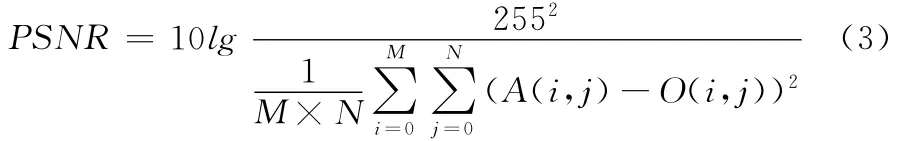
式中：O——加噪前原始图像，A——加噪后经过滤波处理输出的图像，（i，j）——像素点坐标，图像大小为M×N。为测试本文提出算法的性能，以常用的512×512的原始灰度图像Lena和Baboon为例，对其添加不同密度的椒盐噪声后进行滤波处理，并与同类的滤波方法的处理结果进行对比。原始图像如图1所示。

图1 原始图像

图2和图3分别为Lena（512×512）和Baboon（512×512）图像加入30%、60%和90%噪声密度后污染的图像及其相应的经本文滤波算法处理后输出的图像。

由图2和图3的主观视觉效果可以看出，经过本文滤波算法处理后的图像质量明显得到了提高。即使是对原图添加高达90%的极强噪声，噪声图像已经严重失真的情况下，经本文算法滤波处理后都能很好地恢复出原图像中的基本信息，图像细节保护完整，视觉效果好。

为了验证本文算法的滤波性能良好，对标准测试图像Lena（512×512）、Baboon （512×512）、Barbara （512×512）、Boat（512×512）和Peppers （512×512）分别采用3×3的开关中值滤波 （SMF）、递进开关中值滤波（PSM）、极值中值滤波 （EM）以及17×17的自适应中值滤波 （AMF）为代表的4种传统滤波算法和本文算法在不同噪声密度下进行滤波处理。表2分别记录了各种算法在测试图像低噪声密度 （20%）、中噪声密度 （50%）和高噪声密度 （80%）下的PSNR仿真结果。

表2 不同图像各种滤波方法PSNR比较

从表2的客观数据中可以看出不论图像内容和噪声密度的大小，本文滤波算法所得PSNR值均高于同一标准下的传统滤波方法。

图4和图5分别为各种算法对加入不同噪声密度（10%－90%）的Lena（512×512）和Baboon （512×512）图像进行去噪处理所得的PSNR值的比较。

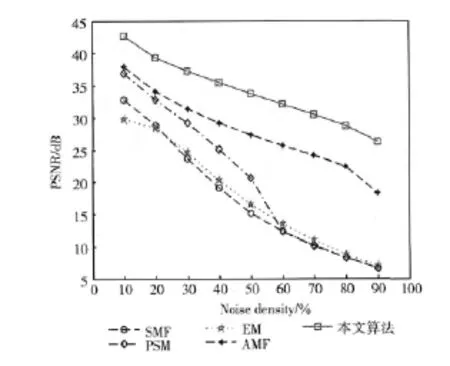
图4 lena在不同噪声密度下各种滤波方法PSNR比较

由图4和图5可见，SMF，PSMF和EM这3种滤波算法性能相近，随着噪声密度的增大，图像质量急剧下降，均不适合用于高噪声密度图像的滤波处理。AMF算法性能比较稳定，效率比较高，但在同一噪声密度下的PSNR均明显低于本文算法。噪声密度越大，本文算法的优势越明显。

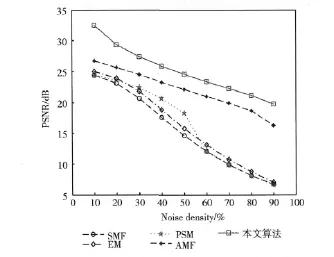
图5 Baboon在不同噪声密度下各种滤波方法PSNR比较

4 结束语

本文用训练好的BP神经网络对图像中的椒盐噪声进行检测，通过大量实验证明了此噪声检测方法的准确率非常高，性能稳定，为后续滤波处理奠定了基础。然后对检测出的噪声点采用自适应加权均值滤波方法进行滤除，非噪声点则保持不变。而且在对图像噪声点进行滤除的过程中，只有窗口中的非噪声点参与了加权运算，高效滤波的同时保护了图像的细节，即使图像纹理比较丰富或者高噪声密度下仍然可以得到较理想的效果。最后通过与其它算法的对比实验，进一步表明了本文算法滤波性能的优越性。

［1］WU Zhong，KE Qifa，SUN Jian，et al.Scalable face image retrieval with identity－based quantization and multireference reranking ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33 （10）：1991－2001.

［2］Charalampidis D.Steerable weighted median fiters ［J］.IEEE Trans on Image Processing，2010，19 （4）：882－894.

［3］YUAN Haidong.Blind forensics of median filtering in digital images ［J］.IEEE Trans on Information Forensics and Security，2011，6 （4）：1335－1345.

［4］Soon Ting Boo，Ibrahim H，Toh K K V.An improved progressive switching median filter ［C］／／Wuhan，China：International Conference on Future Computer and Communication，2009：136－139.

［5］SHI Junyan，LIU Shudan.Dynamic window－based adaptive median filter algorithm ［J］.Computer Engineering and Design，2011，32 （9）：3115－3118 （in Chinese）［时军艳，刘树聃.基于噪声检测的自适应中值滤波算法 ［J］.计算机工程与设计，2011，32 （9）：3115－3118.］

［6］CHANG Ruina，MU Xiaomin，YANG Shouyi，et al.Adaptive weighted average filtering algorithm based on medium value［J］.Computer Engineering and Design，2008，29 （16）：4257－4259（in Chinese）［常瑞娜，穆晓敏，杨守义，等.基于中值的自适应均值滤波算法 ［J］，计算机工程与设计，2008，29 （16）：4257－4259.］

［7］Pankaj Kumar Sa，Banshidhar Majhi.An improved adaptive impulsive noise suppression scheme for digital images ［J］.International Journal of Electronics and Communications，2010，64 （4）：322－328.

［8］DONG Y Q，CHAN R H，Xu S F.A detection statistic for random－valued impulse noise ［J］.IEEE Trans.Image Processing，2007，16 （4）：1112－1120.

［9］LI Xiuling，HE Jinsong.Weight median filter based on rotation invariant pixel correlations ［J］.Journal of Image and Graphics，2010，15 （1）：56－62 （in Chinese）［李秀玲，何劲松.基于旋转不变像素相关性的加权中值滤波器 ［J］.中国图象图形学报，2010，15 （1）：56－62.］

［10］Kaliraj G，Baskar S.An efficient approach for the removal of impulse noise from the corrupted image using neural network based impulse detector ［J］.Image and Vision Computing，2010，28 （3）：458－466.

［11］QIN Ran.Edge information extraction algorithm for CT cerebrovascular medical image based on neural network ［J］.Journal of Electronic Measurement and Instrument，2010，24 （4）：346－352.

［12］LI Tao，YE Xiaoling.Improved stability criteria of neural networks with time－varying delays：An augmented LKF approach ［J］.Neurocomputing，2010，73 （4－6）：1038－1047.

［13］XIA Min，FANG Jian’an，TANG Yang，et al.Dynamic depression control of chaotic neural networks for associative memory ［J］.Neurocomputing，2010，73 （4－6）：776－783.

［14］YE Xiaoling，QIAN Lei，HU Kai.An adaptive denoising method for salt and pepper noise detected by neural network ［J］.Opto－Electronic Engineering，2011，38 （3）：119－124 （in Chinese）［叶小岭，钱蕾，胡凯.神经网络识别图像椒盐噪声的自适应滤波方法 ［J］.光电工程，2011，38 （3）：119－124.］

［15］Nur Zahrati Janah，Baharum Baharudin.Mixed impulse fuzzy filter based on MAD，ROAD，and genetic algorithms ［C］／／Malacca，Malaysia：International Conference of Soft Computing and Pattern Recognition，2009：82－87.