认知无线电中一种n步串行信道感知策略

郑红燕，冯延蓬，仵 博，2，孟宪军

（1.深圳职业技术学院 教育技术与信息中心，广东 深圳518055；2.中南大学 信息科学与工程学院，湖南 长沙410083）

0 引 言

频谱资源匮乏、利用率低的问题已成为制约无线通信发展的主要因素之一，具有无线环境认知能力、动态频谱管理能力、重配置能力的新一代认知无线电 （cognitive radio，CR）技术［1］，允许部分非授权用户 （以下称 “认知用户”）在不影响授权用户 （primary user，PU）的前提下，机会式的利用空闲频谱段进行通信，为频谱资源共享问题提供了一个全新的方向，得到国内外学者的广泛关注，成为通信领域研究的热点［2，3］。频谱感知是认知无线电中实现动态频谱共享的前提和关键［4］。

目前针对MAC层的频谱感知技术研究已经趋于成熟，但针对频谱感知机制的研究却相对较少。在文献 ［5］中，提出随机搜索、串行搜索机制、n－步串行搜索机制，并指出相邻的信道之间在频谱占用规律上具有相关性，采用n－步串行搜索机制可以减少平均检测信道个数，同时保证信道检测的性能，但未考虑认知用户在被迫中断后需检测时的搜索策略。文献 ［6］提出一种停止规则 （stopping rule），将信道感知和接入判决问题转化为获取最大吞吐量的最优求解问题。文献 ［7］引入部分可观察马尔可夫决策过程 （partially observable Markov decision process，POMDP）对认知无线电信道感知策略进行建模，按照信道空闲概率进行排序，求取最优感知信道，但由于POMDP中的状态信念空间求解是一个维数灾问题，难以满足认知用户信道搜索的实时性要求。

本文基于多认知用户集中式协作感知思想，提出一种带缓冲区的双周期n步串行协作感知机制。该机制利用多认知用户分时、分段协作感知，建立空闲信道频谱池，既减小单用户频谱感知与数据传输时间占比，又缩短中断后信道切换时间。此外，还建立离散马尔可夫信道感知参数优化模型，通过量化分析感知模式、感知周期、信道分段数与感知性能的关系，建立信道转移概率和报酬函数模型，并利用值迭代算法求解最优感知参数，在保证频谱感知效率的同时，减小认知用户的被迫中断时间。

1 带频谱池的n步串行协作信道搜索机制

1.1 系统描述

认知无线网络按系统架构可以划分为集中式和分布式［8］，其中，集中式网络架构是由一个或多个集中的实体协调频谱资源，称为认知基站 （或称频谱管理单元），如IEEE802.22系统；分布式网络架构频谱资源管理则依靠点到点的连接分布在各个认知无线终端上，如Cognet系统，但随着终端数量的增加，它们之间的连接数目会呈指数增长，通信和管理成本较高。因此，本文针对集中式认知无线网络的信道共享技术展开研究，网络模型如图1所示。

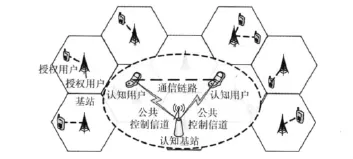
图1 集中式信道共享认知无线网络模型

假设认知无线网络中存在P个授权用户、M个认知用户和N个信道，存在一个具有较高运算能力认知基站，该基站通过一个全局公共控制信道来收集认知用户信道感知信息，建立和维护动态频谱池，并对认知用户的信道感知参数进行分配，包括按何种顺序、对哪些信道开始搜索、优化信道感知周期等，目的在于提高认知用户的感知准确度和信道利用率。

在每个时隙，每个信道有Busy和Free两种状态，Busy表示信道被占用，Free则表示信道空闲。空闲信道允许认知用户采用Overlay的方式机会式接入，并假设每个认知用户每个时隙只能占用一个信道。

1.2 n步串行信道搜索机制及频谱池建立

在认知无线电技术的实际应用环境中，认知用户受自身硬件成本、感知能力等的限制［9］，使得单一认知用户感知范围、感知精度有限；认知用户通信信道被授权用户抢占时，认知用户被迫重新搜索新的空闲信道 （称之为按需搜索），需重新进行多信道搜索，感知时间较长，会大大影响认知用户通信QoS。针对以上问题，本文基于链路层的多认知用户集中式协作感知思想，提出一种带频谱池的n－步串行 协 作 搜 索 机 制 （n－step serial search with spectrum pool，n－SSSP），通过多认知用户分时、分段协作，有效减小单用户频谱感知与数据传输时间比，提高频谱感知效率。

由于相邻信道间的信道占用规律具有一定相关性，认知用户在进行信道感知时，串行顺序检测可能遭遇连续的非空闲信道，增大频谱感知时间。n－SSSP的基本思想如下：由基站将频谱划分为Nsection段，每段固定包含n个信道，n＝?N／Nsection」。每个加入认知网络的认知用户，在首个感知周期内，主动从认知基站获取一个随机的起始信道号i，以n为步长进行搜索，直到遍历每个信道段的第i信道。如果认知用户在该轮搜索中未感知到空闲信道，则重新从认知基站获取新的信道号i′，并以n为步长对Nsection个信道段进行新的遍历，如此反复，直到搜索到空闲信道为止。完成信道感知后，认知用户根据自身带宽需求，在感知到的一个空闲信道中选择一个合适信道接入，并把剩余感知到的空闲信道号上报给基站，基站将认知用户的感知信息进行与操作，构成频谱池。基本原理如图2所示。

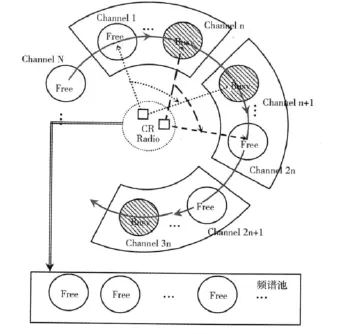
图2 n－步串行协作频谱搜索机制

与传统搜索机制不同，n－SSSP在认知用户搜索到空闲信道后，并不马上停止，而是继续完成所有Nsection段的信道遍历，并将盈余的空闲信道信息上报基站，建立空闲频谱池。频谱池用来向被中断的认知用户提供搜索的信道号。当认知用户通信信道被授权用户抢占时，认知用户不再从基站随机获取信道号，而是通过认知基站获取频谱池中的信道号，由于频谱池中的信道为感知后验证的空闲信道，因此被再次感知到是空闲信道的概率将大大提高，从而有效缩短认知用户通信被迫中断后的频谱感知时间。认知用户在获得频谱池中的信道号之后，再通过本地感知寻找可使用的空闲信道。

1.3 双周期搜索策略

为保证频谱池的时效性，并进一步提高认知用户频谱感知效率，减小频谱感知与数据传输时间占比，在n－SSSP的基础上提出一种双周期感知策略，所谓双周期，是指认知基站为所有认知用户指定一个频谱池更新周期T1，再将T1划分为若干个相等的感知周期T2。如图3所示。

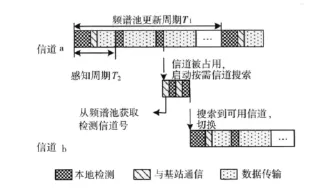
图3 双周期机制

对于每个认知用户，无论通信是否被中断，每隔T1时间，必须从基站获取一个信道号i，并以n为步长对每个信道段内的第i个信道进行感知，并将除自用外的剩余空闲信道信息上报给认知基站，并由认知基站对多认知用户感知信息进行汇聚和融合，更新频谱池，以备被中断用户使用，该过程称为：共享式频谱感知。

每个感知周期T1的首个感知周期T2即用来共享式频谱感知，它完成包含本地检测、与基站通信和数据传输3个部分，除首个感知周期外，其余感知周期在时间上与T2一致，正常情况下仅包含本地检测和数据传输两个部分，认知用户只需对自身接入的信道进行感知，如果该信道仍为空闲状态，则继续使用，无需与基站通信；如果信道被授权用户占用，则触发按需信道搜索，由认知用户从频谱池中获取一个空闲概率较高的信道进行感知，以便快速回复通信。相比传统周期性感知机制，无需每个周期都进行多个信道的感知，特别是中断后，能快速找到新的空闲信道，这样认知用户用于感知信道的时间将大大缩短，为数据传输预留更多时间，可以提高感知效率，缩短响应时间。

2 搜索步长及感知周期优化

搜索步长n以及频谱池更新周期T1和感知周期T2的设定将直接影响到频谱感知效率和频谱池的时间有效性。因此，本文提出一种基于马尔可夫决策过程 （Markov decision process，MDP）的n－SSSP感知参数优化模型 （以下简称为：MDP－SSSP），综合考虑频谱感知效率、用户被中断时间两要素构建报酬函数，并通过值迭代算法求取搜索步长和感知周期的最优解。

2.1 基于MDP的感知参数优化模型建立

MDP模型是在给定当前知识和信息的情况下，预测和决策未来，可以用一个四元组 ＜S，A，T，R＞ 表示［10］。其中，S表示状态集，表示所有可能到达的状态；A表示动作集，表示所有可能执行的动作；T：S×A→ ∏（S）为状态转移函数，表示在状态s下执行a到达状态s′的概率，记为T（s，a，s′）；R：S×A→R表示策略评价函数。

（1）状态集和动作集定义

建立离散时间MDP模型，t表示当前时刻，t′表示下一时刻，t′＝t＋ΔT，其中，ΔT即为认知用户感知周期，故：ΔT＝T2。

设

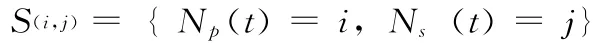
其中，Np（t）和Ns（t）分别为系统在t时刻的授权用户和认知用户的数量，则系统状态集可表示为

动作集包含系统待优化的参数，本文以搜索步长和感知周期为优化目标。特别的，针对感知周期，选取频谱池更新周期T1和感知周期T2均为优化参数，为降低模型求解难度，以T2基本时间单位，定义双感知周期比τ（τ＝T2／T1）为优化目标。则系统动作集可表示为

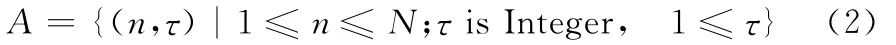
（2）状态转移概率建模

状态转移函数表示信道状态在相邻两个时间片上的变化，与系统业务模型紧密相关，为了求取状态转移概率，对系统业务流进行建模。

定理1 对系统中认知用户与授权用户流量利用随机过程进行建模，假定授权用户与认知用户的到达流量均满足泊松随机过程，其到达率分别为λp、λs；频谱使用的持续时间满足负指数分布，平均占用时间分别为：1／μp和1／μs，认知用户每次仅能够接入一个空闲信道，且忽略一个时隙内认知用户因为授权用户的出现而让出相应信道的时间，则系统状态转移概率如下

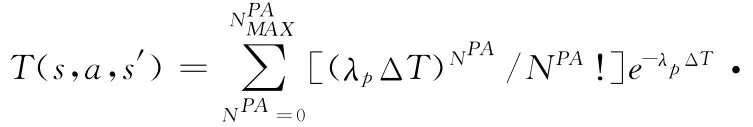
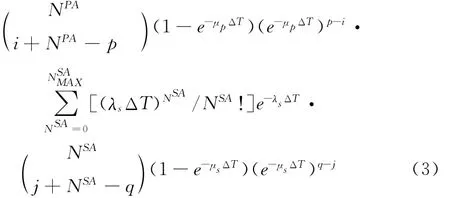
证明：设NA∈｛NPA，NSA｝为授权用户和认知用户的在间隔ΔT内的到达数，ND∈｛NPD，NSD｝为授权用户和认知用户在间隔ΔT内的离开数。PA（NPA）和PA（NSA）表示在间隔ΔT内到达NPA和NSA个授权／认知用户的概率，PD（ND＝m，k）表示在间隔ΔT内从m 中离开k个授权／认知用户的概率。

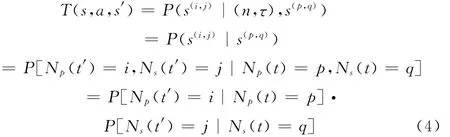
根据系统业务模型可知授权用户和认知用户到达率λp和λs，那么在间隔ΔT内，由泊松过程的状态概率分布可知，到达NPA个授权用户和NSA个认知用户的概率分别为

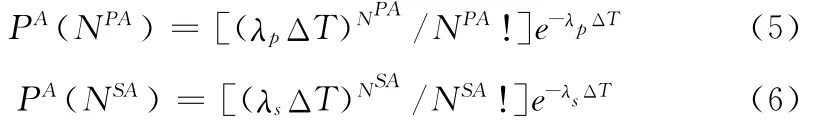
频谱使用的持续时间满足负指数分布，平均占用时间分别为：1／μp和1／μs，则从m中离开k个授权用户和认知用户的概率［11］为

同样有

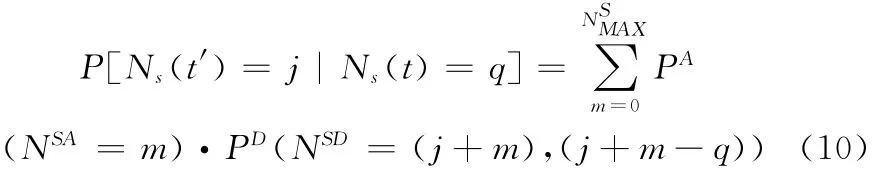
将式（6）－式（10）代入式（4）可得

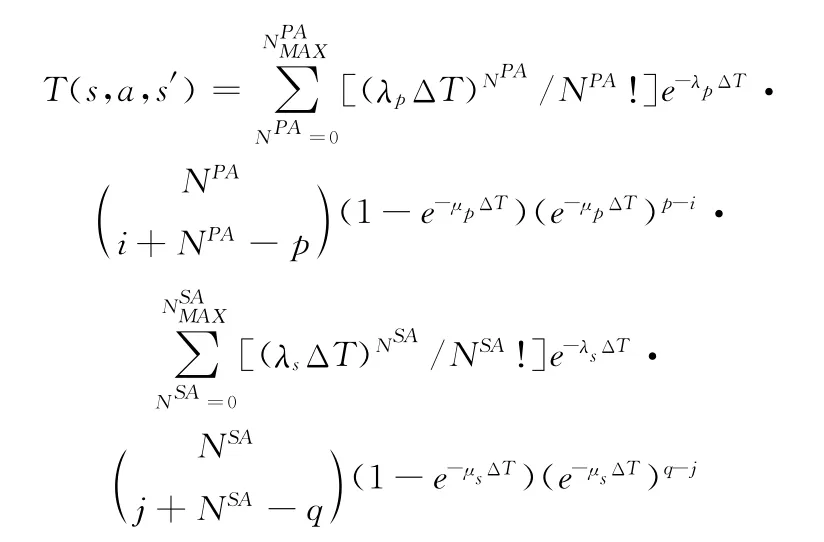
证毕。

（3）性能指标及报酬函数建模

由图2可知，在正常情况下，在首个感知周期T2内，认知用户需执行进行本地感知、上报基站和数据传输3个动作，其余感知周期，只需检测本占用信道和进行数据传输，那么设认知用户对单位信道的本地感知花费时间为Tsense，与基站通信花费的时间为Ttransport，不考虑认知用户因被中断触发的按需感知时的感知效率，可以得出认知用户在非中断时的感知效率为

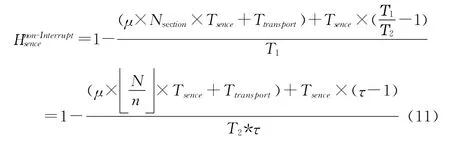
式中：μ——认知用户首次感知到空闲信道所需要轮询的圈数，由授权用户占用信道密度和分布决定，授权用户占用信道密度越大，信道越繁忙，被检测信道内不包含空闲信道的概率越大，则认知用户首次感知到空闲信道所需的轮询的圈数也就越大。

在用户被中断时，直接从频谱池获取信道进行感知，并进行数据传输，仍然以一个感知周期作为一次中断检测评价单位，则认知用户在中断时的感知效率为

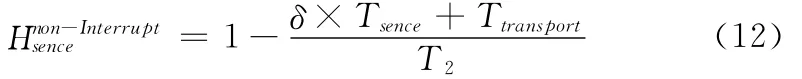
式中：δ——认知用户中断后重新感知到新的空闲信道所需要检测的信道数，与认知被中断概率、被中断时间相关，可通过离线训练获取。

信道感知效率Ηsence可定义为认知用户在中断和非中断时感知效率的加权和

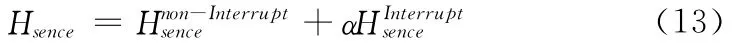
式中：α——加权因子，与认知用户被中断概率相关。

除感知效率外，认知用户被迫中断时间Τinterrupt与搜索步长n和双感知周期比τ也紧密相关。在相同的授权用户到达率和检测周期Τ2下，认知用户被迫中断概率随授权用户到率的增大而增大，业务中断后，利用频谱池中预留空闲组建新的会话，频谱池更新周期Τ1越小，则频谱池中的信道空闲概率越高，认知用户在业务中断后能越快搜索到新的空闲信道，即中断时间Τinterrupt越小。

可以看出感知效率和被迫中断时间是一对矛盾的性能指标，为保证认知用户有较高的感知效率Ηsence和较小的中断时间Τinterrupt，设系统报酬函数如下

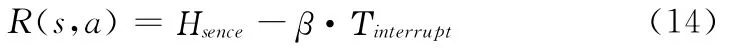
感知效率越高，业务被迫中断时间越小，则系统报酬值越大，反之越小。其中β为被迫中断时间权重调节因子，可以针对不同的认知业务进行调节，如：对于QoS要求较高的语音业务，则增大β取值，通过适量牺牲感知效率来获得更低的业务被迫中断时间Τinterrupt，反之，对于QoS要求较低的数据业务，则可以减小β取值。

2.2 算法求解

经过对认知网络进行MDP建模，认知用户频谱感知周期优化问题转化为MDP报酬函数的最大化问题，报酬值越大，频谱感知性能越好。本文采用值迭代算法［12］获取MDP最大报酬值，具体描述见表1。其中，Vt（s）通过Bellman方程计算，代表模型在不同状态的值函数，γ为折扣因子；最优策略π＊t（s）是使折扣报酬值和的期望值最大时的动作取值。

表1 MDP求解算法

3 仿真结果

本文从两个角度评价带频谱池的双周期n－步串行协作信道感知策略的有效性。首先，针对本文算法在不同搜索步长n和双感知周期比τ下的性能进行仿真和纵向对比，验证参数优化前后对算法性能的影响；其次分别实现本文算法与随机搜索、传统串行搜索算法，在不同的授权用户到达率λp下的性能指标进行横向对比，验证本文算法的有效性，仿真参数见表2。

利用Matlab搭建仿真实验平台，开展两组实验，每组实验分别重复10次求平均值，每次实验运行30分钟。

（1）为了对比n－SSSP和MDP－SSSP算法性能，并验证参数对（n，τ）与感知效率Ηsence和被迫中断时间Τinterrupt之间的关系，首先，固定参数τ，倍数逐渐增大n抽取（n，τ）＝（1，3）、（2，3）、（4，3）、（8，3）、（16，3）5组参数，然后，固定参数n，逐渐增大τ抽取 （n，τ）＝ （4，1）、（4，2）、（4，4）、（4，5）4组参数分别进行实验，将结果与MDP－SSSP进行对比，结果如图4 （a）、（b）所示。

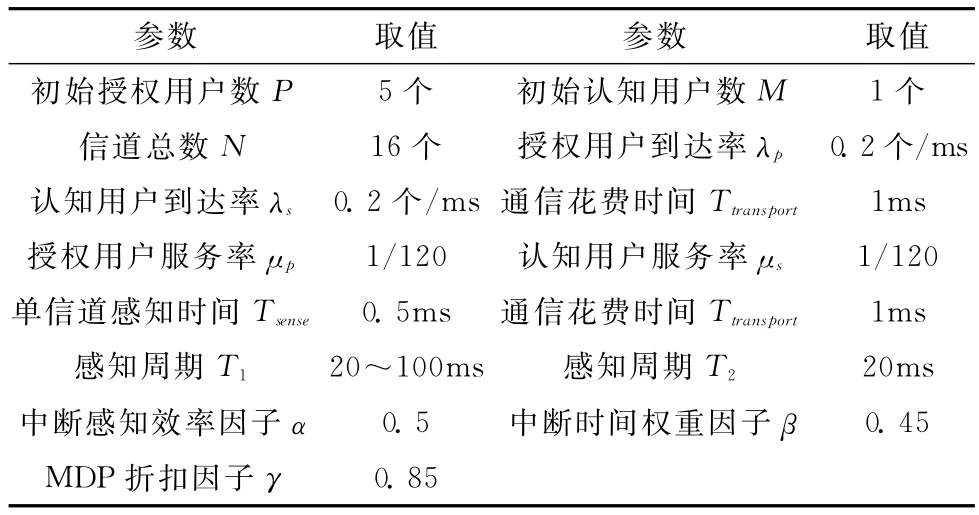
表2 仿真环境参数

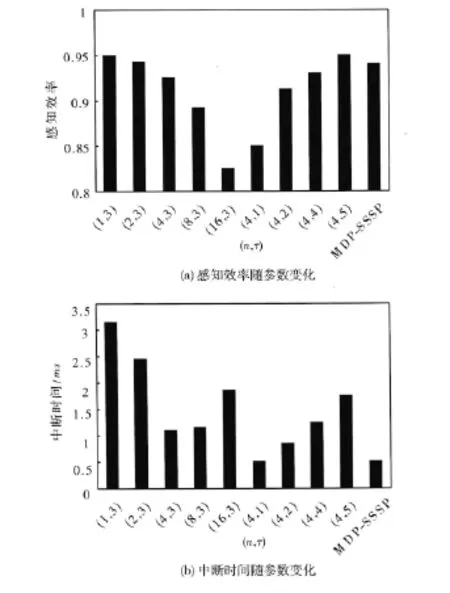
图4 感知效率和中断时间随参数变化

就图4（a）、（b）单独而言，在τ保持不变时，感知效率随n的增大而减小，在n保持不变时，感知效率随τ的增大而增大；被迫中断时间则与n和τ无明显线性关系，但综合两个图发现，在实验抽取（n，τ）参数对中，感知效率最优时，被迫中断时间则很长，被迫中断时间最优时，则感知效率偏低。而采用MDP－SSSP算法，两项指标参数虽然不是最优，但可以平衡各项指标，获取最优参数，提高系统的整体性能。

（2）将 MDP－SSSP与随机搜索 （random search，RS）、传统串行搜索算法 （serial search，SS）比对，认知用户被迫中断概率、感知效率Ηsence和中断时间Τinterrupt随授权用户到达率λp变化情况如图5 （a）、（b）、（c）所示。

图5 信道关键指标随授权用户到达率变化

MDP－SSSP的平均感知效率为0.74，而RS和SS的平均感知效率分别为0.53和0.36，由于采用了 MDP建模和针对感知效率的求解算法，在感知效率上MDP－SSSP具有明显优势。由于采用了双周期搜索策略，MDP－SSSP的被中断率和中断时间都优于RS和SS。RS和SS的平均被中断率比较接近，MDP－SSSP的平均被中断率为0.398，比RS和SS低20%。RS和SS的平均中断时间分别为MDPSSSP的2倍和2.2倍，因此MDP－SSSP可以使认知用户在被授权用户中断后更快地找到可用信道。

由此可见，MDP－SSSP算法在感知效率Ηsence，被中断概率和中断时间Τinterrupt三项性能指标上均优于传统频谱感知机制，尤其是在授权用户到达率较高，信道占用率提高的情况下，仍能保证在较高感知效率下，实现较低的中断时间，从而有效保证了认知用户的通信质量。

4 结束语

本文综合考虑信道检测效率和认知用户被迫中断时间两个因素，提出了带频谱池的n步串行信道搜索策略，在认知用户被迫中断后，通过频谱池中的先验信道感知信息，快速搜索到新的空闲信道，通过构建离散马尔可夫模型，求取参数最优解，通过仿真实验验证，表明引入频谱池和MDP优化模型的MDP－SSSP策略相比随机搜索和串行搜索，能显著地提高信道感知效率，缩短认知用户被迫中断时间。

［1］Mitola Joseph.The inventor of cognitive radio ［J］.Electronic Engineering Times，2005 （1）：47－50.

［2］Srinivasa S，Jafar S A.The throughput potential of cognitive radio：A theoretical perspective ［J］.IEEE Communications Magazine，2007，45 （5）：73－79.

［3］WEI Jibo，WANG Shan，ZHAO Haitao.Cognitive wireless networks：Key techniques and sate of the art ［J］.Journal on Communications，2011，32 （11）：147－158 （in Chinese）.［魏急波，王杉，赵海涛.认知无线网络：关键技术与研究现状［J］.通信学报，2011，32 （11）：147－158.］

［4］Ghasemi A，Sousa E S.Spectrum sensing in cognitive radio networks：Requirements，challenges and design trade－offs ［J］.IEEE Communications Magazine，2008，46 （4）：32－39.

［5］Ling Luo，Sumit Roy.Analysis of search schemes in cognitive radio ［C］／／San Diego：2nd IEEE Workshop on Networking Technologies for Software Define Radio Networks，2007：17－24.

［6］Jia J，Zhang Q，Shen X.HC＿MAC：A hardware－constrained cognitive MAC for efficient spectrum management ［J］.IEEE Journal on Selected Areas in Communications，2008，26（1）：104－117.

［7］Jayakrishnan Unnikrishnan，Venugopal V Veeravalli.Algorithms for dynamic spectrum access with learning for cognitive radio ［J］.IEEE Transactions on Signal Processing，2010，58（2）：750－760.

［8］MIAO Dan.Research on dynamic spectrum allocation technology in cognitive wireless network ［D］.Beijing：Beijing University of Posts and Telecommunications，2010：27－29 （in Chinese）. ［苗丹.认知无线网络中的动态频谱分配技术研究［D］.北京：北京邮电大学，2010：27－29.］

［9］Yunxia Chen，Qing Zhao，Ananthram Swami.Joint design and separation principle for opportunistic spectrum access in the presence of sensing errors ［J］.IEEE Transactions on Information Theory，2008，54 （5）：2053－2071.

［10］Bhatnagar S，Abdulla M S.Simulation－based optimization algorithms for finite－horizon Markov decision processes ［J］.Simulation，2008，84 （12）：577－600.

［11］Xavier Gelabert，Oriol Sallent.Spectrum sharing in cognitive radio networks with imperfect sensing：A discrete－time Markov model［J］.Computer Networks，2010，54 （14）：2519－2536.

［12］Stevens－Navarro E，Yuxia Lin，Wong V W S.An MDP－based vertical handoff decision algorithm for heterogeneous wireless networks ［J］.IEEE Transactions on Vehicular Technology，2008，57 （2）：1243－1254.