改进的基于α扩展移动的立体匹配算法

李惠光，翁良宝，姜洪磊

（燕山大学 电气工程学院，河北 秦皇岛066004）

0 引 言

立体匹配在计算机视觉研究是一个重要领域。它通过匹配给定的两幅或多幅图像，寻找图像中的物体在另一张图像中相对应点的关系，计算出两者之间的视差 （Disparity），从而获得物体深度等信息［1］。近年来，随着图论的发展和完善，图割思想的算法在立体匹配方面逐渐成为一个热点［2－3］，其中，由 Boykov等人［4－5］提 出 的α 扩 展 移 动 算 法的应用较为广泛，该算法的匹配精度高，尤其在底纹理区域和不连续区域的匹配也可以获得良好地匹配效果［6］，但是，α扩展移动算法在匹配过程中需要不断构建网格图，进行图切割优化，这占用了大量的计算时间，针对这一问题，本文提出了一种改进的α扩展算法，该算法首先定义了一个循环停止参数，当计算的循环停止参数满足循环停止条件时，停止循环，其次是改变了传统α扩展移动算法的无序迭代，优先设定经初始视差计算后大概率分布视差值。

1 α扩展移动算法的相关知识

1.1 构造能量函数

计算机视觉里的很多问题都可以归结为能量函数的优化问题［7］，比如图像的立体匹配问题，可以通过构造能量函数，采用优化算法求解能量函数的最小值，与最小值对应的像素标记的视差值就是匹配的结果。

立体匹配的能量函数一般由数据项约束Edata（f）和光滑项约束Esmooth（f）组成，如下

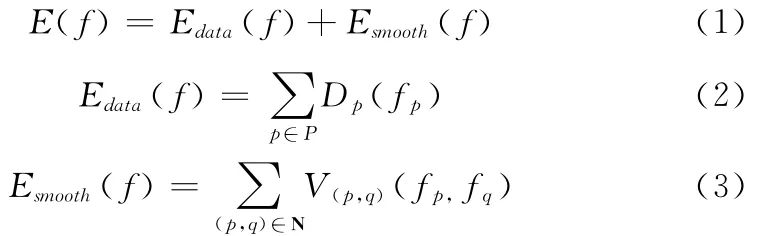
则能量函数可以表示为

式中：P——图片所有像素点的集合，p——集合中的一个像素点，｛p，q｝∈N——图片中相邻的两个像素点，fp∈L——p的标记视差，L——视差范围，则 Dp（fp）——p点在视差为fp时匹配代价，它的表达式为

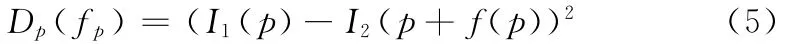
式 （3）是图像中相邻像素间的惩罚项，它反应了区域内部的连续性和边界的不连续性。本文选用了Potts模型的平滑项函数

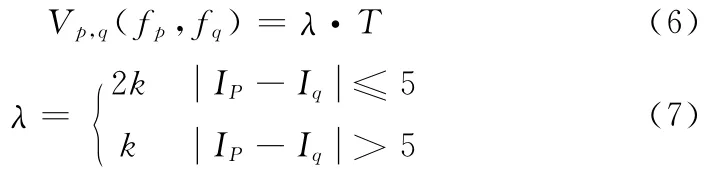
其中k＝20，当fp＝fq时，T＝0；fp≠fq时，T＝1。

1.2 α扩展移动算法具体描述

由于能量函数E（f）的最小化求解是一个非确定性多项式问题，如果采用穷举法，则算法的计算量过大，它的状态空间为LH×W，其中L为视差范围，H为图片的高度，W为图片的宽度；采用变分方法或者条件迭代模式算法 （iterated conditional mode，ICM 算法），在求解的过程中容易遇到对初始值敏感、易得到局部极小值的问题，因此，如何计算出全局最小值一直是个难题。针对这个问题，Boykov采用了ICM算法循环迭代的思想［8］，通过α扩展移动对求得的能量函数不断迭代循环，使其最终收敛于最小值。与ICM算法不同的是α扩展移动算法是同时改变大部分的像素标记视差值，每次扩展移动都会使能量函数有很大变化，这样就很好的克服了ICM算法的单个像素的移动中容易遇到局部极小值的问题，使能量函数向全局最小值收敛。α扩展移动算法的流程图如图1所示。

图1 α扩展移动算法流程

a在流程图中，步骤3到步骤5的执行称为一次内部迭代，在内部迭代的过程，α是在视差的范围里随机设定的，步骤2到步骤5的执行称为一次外部循环。其中，步骤中如何计算f＾＝argminE（f′）是一个非常关键的问题，Boykov构建了α扩展移动能量网格图，首先对所有视差标记不为α的像素点建立能量网格图，然后通过最大流最小割算法对能量网格图进行 “切割”（可以简单理解为优化），“切割优化”的结果使其中的部分像素视差被重新标记为α，而剩余的则保持原来不变的视差标记［9］。α扩展移动算法采用这样的优化方式不断循环修改每个像素的视差标记值，使能量函数逐渐收敛，最终收敛到全局最小值。

1.3 能量网格图的构造

图2为α扩展移动时构造的能量网格图，为方便理解，把Gα设置成一维图像。

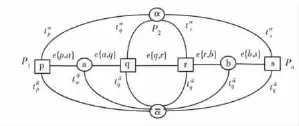
图2 α扩展移动算法网格

对于每个像素点p∈P通过t－linktap和t珔ap连接到源点α和汇点珔α，构造的辅助节点a｛p，q｝通过辅助边ε｛p，q｝＝｛e｛p，a｝，e｛a，q｝，t珔αα｝连接到p，q，珔α点，所以图2中所有点的连接边为

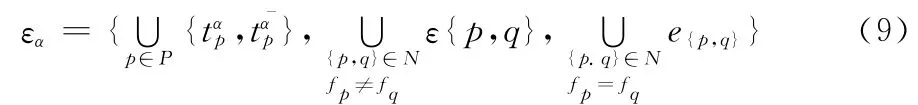
各个连接边的权值容量大小设置见表1。

表1 连接边的权值设置

1.4 最大流最小割求解能量函数

在构建完能量网格图后，利用最大流最小割求解能量函数E（f∧）。本文采用的是Boykov和Kolmogorov提出的最大流最小割算法，该算法是一种双向搜索并重用搜索树的增广路径算法，虽然算法的理论复杂度比较高，为，其中s是最大流算法的最大增广数目，m和n分别是网格图中的连接边和节点，iter是收敛时需要迭代的次数，k是视差的数目，但是计算机视觉的实际应用中却有着非常高的效率［10］，比其他最大流算法快了2～5倍，因此在立体匹配、图像恢复等方面广泛使用。

2 改进的α扩展移动算法

为分析匹配算法的性能，本文采用均方根误差 （式（10））和错误匹配率 （式 （11））两个指标

其中dc（x，y）是算法计算所得的视差值，dGT（x，y）是真实的视差值，δd是容许的错误视差阈值，本文中δd＝1。

2.1 构造循环停止参数简化循环过程

以 Middlebury［11］提供的标准图 Tsukuba （384＊288）为例，图3为经过第i次循环后的视差值分布图。

图3 第i次循环后的视差值分布

本文以视差fp在视差值分布图中的分布概率构造一个向量P，按照式 （12）构造一个循环停止参数θ

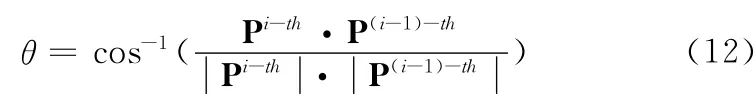
图4是Tsukuba在α扩展移动后的能量函数E（f）变化图，Run0为随机标记视差后的能量函数的初始状态。仔细观察可以发现在最初的几次外部循环后能量函数值 （直方柱表示）迅速下降，随着循环次数的不断增加而逐渐单调递减，一直衰减到能量函数最小值时停止循环。然而，在不断循环的过程中，能量函数值在接近最小值时，其收敛速度明显减小，变化也越来越微弱，这说明α扩展移动算法的在后面的几个循环中的效率越来越低。

图4 循环过程中能量函数E（f）与Theta（θ）的变化

为了更全面的研究α扩展移动算法，本文也通过误匹配率和均方根误差这两个指标去分析外部循环过程中的其他变化。如图5所示，同样也可以发现，随着不断地循环，误匹配率和均方根误差也逐渐单调减小，最后缓慢的收敛于最小值。

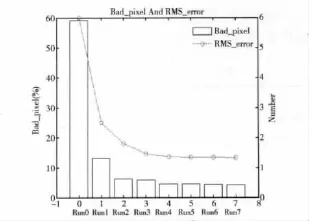
图5 循环过程中误匹配率与均方根误差的变化

针对以上两图的分析，为了提高扩展移动算法的计算效率，节省算法的运行时间，根据式 （12）构造的θ，建立新的循环机制，即第i次与第i－1次之间的视差分布变化向量越来越小，当循环停止参数满足循环停止阈值的条件θ＜θthreshold时 （θthreshold为循环停止阈值），就停止继续循环，这样相较于传统的α扩展移动算法的循环过程，就减少了循环过程中能量函数变化很小的区间循环，缩短了算法的计算时间，提高了算法的计算效率。

2.2 改变α扩展移动顺序

在α扩展移动算法的内部迭代过程中，α值的设定是在视差值范围［fmin，fmax］随机选取的。如果将α值按照标准视差分布图中大概率的视差值优先设定，那么与其他的α小概率分布视差值相比，在进行α扩展移动时能量函数的变化会有更大的影响。因此，本文采用了将待匹配的图像进行初始视差计算的方法，将α按照计算后的初始视差大概率分布视差值优先设定，这样在内部迭代的过程中，能量函数能以更快的速度收敛于最小值。

由于初始视差计算的方法对视差计算的匹配精度结果要求不高，只要求计算出视差值范围内的大概率视差值，本文选择了基于区域的局部匹配算法中的SAD算法 （sum of absolute differences）。SAD算法是在左图中待匹配像素点创建一个n×n的窗口，然后沿着极线在右图视差范围内选择相似性最大的像素点作为匹配点。

2.3 改进的α扩展移动算法的流程图

图6是改进的α扩展移动算法的流程图。和原始的流程图比较，本文对步骤2、步骤7和步骤8做了修改，在步骤2中，优先将α按照初始视差计算后的大概率视差值设定，步骤7中，增加了θ的计算，步骤8中，增加一个阈值判定，即当计算的θ满足循环停止阈值时就不再进行循环，计算停止，反之，则继续循环。阈值θthreshold的选择严重影响着算法的匹配时间和精度。表2是以Tsukuba为例在不同θthreshold条件下的实验结果，如果θthreshold选择过大，算法匹配时间缩短，但算法的匹配精度有很大误差，如果θthreshold选择过小，则算法匹配时间延长，匹配精度提高。本文改进α扩展移动算法选择的θthreshold＝1。

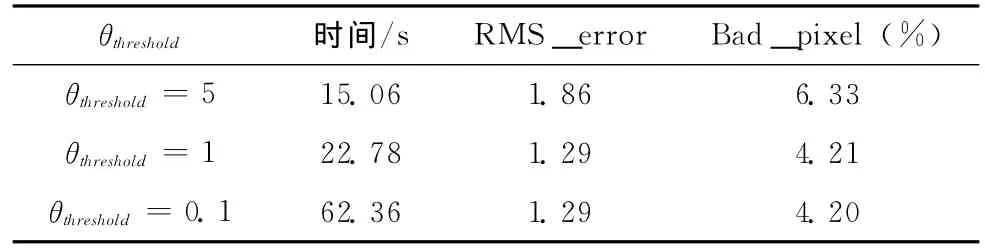
表2 不同θthreshold的实验结果

图6 改进的α扩展移动算法的流程

3 实验和结果

为了验证改进的图割算法的正确性，本文根据Middleburry上提供的标准图像进行了实验，实验的数据结果以匹配时间、均方根误差和错误匹配率作为评价指标。实验图像和数据结果如图7和表3所示。

图7 匹配后的视差图对比

表3 视差图的评价指标对比

根据图7原始算法和改进算法匹配后的视差图对比，直观上观察改进算法获得了几乎和原始算法一致的稠密视差图，根据表格3中的均方根误差和误匹配率的指标对比，原始的α扩展移动算法和改进的α扩展移动算法匹配的都获得了良好的匹配效果，而表格2视差图的匹配时间表明，改进算法比原始算法在效率上却明显提高，计算时间大大缩短，这是由于构造的循环停止参数满足条件时停止循环，减少算法的循环过程，将α优先按初始匹配后的大概率视差分布设置则使能量函数以更快的速度收敛，这样使改进的算法不仅可以得到精确视差图的同时，匹配时间也大大减小了。

4 结束语

在计算机视觉领域中，采用α扩展移动算法去解决立体匹配问题是一种有效的方法，通过建立能量网格图不断的循环优化求解能量函数最小值，在低纹理区域也可以获得稠密精确的视差图，但该类算法的复杂度很高，匹配时间比较长。本文仔细研究了α扩展移动算法能量函数的优化过程，提出了两个改进，一是在外部循环的过程中提出了循环停止机制，，二是改变了原始算法α设定的随机性。实验结果表明，改进的算法 “遗传了”α扩展移动算法的优点，不仅可以获得几乎一致匹配精确高的稠密视差图，而且在算法的匹配时间大大缩短了，与原始算法比较减少了60～75%。由于α扩展移动也应用于计算机视觉的其他领域如图像恢复和图像分割等方面［12－14］，不同的是能量函数表达式不一样，因此改进的算法也可以在图像处理方面的其他领域里获得应用。

［1］BAI Ming，ZHUANG Yan，WANG Wei.Progress in binocular stereo matching algorithms ［J］.Control and Decision，2008，23 （7）：721－729（in Chinese）.［白明，庄严，王伟.双目立体匹配算法的研究与进展 ［J］.控制与决策，2008，23 （7）：721－729.］

［2］WANG Nian，FAN Yizheng，BAO Wenxia.An images matching algorithm based on graph cuts ［J］ACTA Electronica Sinica，2006，34 （2）：232－236 （in Chinese）.［王年，范益正，鲍文霞.基于图割的图像匹配算法 ［J］.电子学报，2006，34 （2）：232－236.］

［3］ZHANG Lingtao，QU Daokui，XU Fang.An improved stereo matching algorithm based on graph cuts［J］.Robot，2010，32 （1）：215－219（in Chinese）.［张令涛，曲道奎，徐方.一种基于图割的改进立体匹配算法 ［J］.机器人，2010，32 （1）：215－219.］

［4］Boykov Y，Veksler O，Zabih R.Fast approximate energy minimization via graphcuts ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23 （11）：1222－1239.

［5］Kolmogorov V，Zabin R.What energy functions can be minimized via graphcuts ［J］.IEEE Transon Pattern Analysis and Machine Intelligence，2004，26 （2）：147－159.

［6］LU Ali，TANG Zhenmin.Anα－expansion stereo algorithm based on segment－constraint ［J］.PR＆AI，2010，23 （3）：385－395 （in Chinese）.［卢阿丽，唐振民.基于分割约束的α扩展体视算法［J］.模式识别与人工智能，2010，23 （3）：385－395.］

［7］WU Chunhong，FU Guoliang.A stereo matching method based on K－means segmentation and neighborhood constraints relaxation ［J］.Chinese Journal of Computers，2011，34 （4）755－760 （in Chinese）.［伍春洪，付国亮.一种基于图像分割及邻域限制与放松的立体匹配方法 ［J］.计算机学报，2011，34 （4）755－760.］

［8］Gong M.A performance study on different cost aggregation approaches used in real－time stereo matching ［J］.International Journal of Computer Vision，2007，75 （2）：283－296.

［9］XU Sheng，YUN Ting，YE Ning.Research on stereo matching algotithm based on disparity map optimization ［J］.Computer Engineering and Design，2012，33 （2）：658－664 （in Chinese）.［徐昇，云挺，业宁.基于视差图优化的立体匹配算法研究 ［J］.计算机工程与设计，2012，33 （2）：658－664.］

［10］Candemir S，Akgul Y S.Adaptive regularization parameter for graph cut segmentation ［C］／／Proceedings of the 7th International Conference on Image Analysis and Recognition.Springer Berlin Heidelberg，2010：117－126.

［11］Microsoft research of disparity matching algorithm ［EB／OL］.［2009－07－26］.http：／／vision.meiddlebuty.edu／stereo／.

［12］Boykov Y，Funka－Lea G.Graph cuts and efficient N－D image segmentation ［J］.International Journal of Computer Vision，2006，70 （2）：109－131.

［13］Boykov Y，Veksler O.Graph cuts in vision and graphics：Theories and applications ［C］／／Handbook of Mathematical Mode－ls in Computer Vision.New York：Springer US，2006：79－96.

［14］LIU Songtao，YIN Fuliang.The basic principle and its new advances of image segmentation methods based on graph cut［J］.Acta Automatica Sinica，2012，38 （6）：911－922 （in Chinese）.［刘松涛，殷福亮.基于图割的图像分割方法及其新进展 ［J］.自动化学报，2012，38 （6）：911－922.］