快速收敛的克隆选择算法

肖金科，王 刚，刘昌云，付 强

（空军工程大学 防空反导学院，陕西 西安710051）

0 引 言

克 隆 选 择 算 法 （clonal selection algorithm，CLONALG）是Burnet模拟免疫系统抗体生成提出的群智能优化算法，该算法已经广泛应用于模式识别、组合优化、机器学习等领域。然而这种智能优化算法很容易陷入局部最优、收敛慢等缺陷，为此，一些学者对其进行了改进。文献 ［1］以球面杂交方式对种群进行调整并动态修正每个抗体的变异概率的方法，加快了CLONALG的全局收敛速度；文献 ［2］采用的3种变异算子以提高抗体群的多样性，缺乏抗体间的协同进化；文献 ［3］引入了周期变异算子，周期变化的变异率提高了抗体群的多样性，但演化的后期容易破坏优良抗体；文献 ［4］采用多个子种群代替了原来单一的种群，每个子种群独立地进化，在完成一次进化后每个子种群中最好的抗体将取代其它种群最坏的抗体，算法性能得到显著提高。

本文通过深入研究CLONALG的机制，改进了克隆算子和提出云自适应变异算子，引入抗体重组算子，提出了快速收敛于全局最优解的快速收敛的克隆选择算法 （fast convergence clonal selection algorithm，FCCSA）。新型克隆算子模拟了克隆抗体间的竞争和抑制机制，有效控制了相似抗体的数量；云自适应变异，保证了算法先全局搜索，寻找峰值，然后在优良抗体周围局部搜索，寻找最优值；抗体重组算子使得抗体之间信息交互、协同进化。优化10个被广泛应用标准测试函数，与其它常见的优化算法对比，结果表明，FCCSA的性能得到显著提高。

1 CLONALG描述

CLONALG的核心在于增殖克隆算子和变异算子，前者与抗体亲合力成正比，保证抗体群的亲合力逐步增大；后者与抗体亲合力成反比例关系，保留最佳抗体并改进较差抗体。克隆选择策略在理论上保证了抗体群的多样性［5－6］，但深入分析可知，CLONALG只是对复杂免疫系统的简单模拟，算法只是抗体群的进化计算，没有考虑抗体之间的竞争机理；克隆后抗体群的变异过于单一，抗体群多样性有限，对处理复杂的多模态优化问题能力有限，容易早熟［7－8］。

2 FCCSA

不失一般性，设函数优化问题

式中：f（X）——n维解空间的连续实函数，其中L＝ （l1，l2，…，ln）≤X≤U ＝ （u1，u2，…，un），即li≤xi≤ui（i＝1，2，…，n）。设抗体群珡X＝｛X1，X2，X3，…Xq｝，q为抗体群中抗体的个数，抗体 Xi＝ ［x1，…xk－1，xk，…，xn］，i＝1，2，…，q，n为抗体中变量的个数，此抗体－抗原的亲和力记为f（Xi）。

2.1 算法设计

为了提高算法的多模态优化问题的求解能力，结合独特性和抗独型免疫网络的特性，从以下几个方面对CLONALG进行了改进。

（1）克隆算子

抗体受抗原的侵入刺激被激活，克隆增值；同时抗体之间的竞争抑制作用维持免疫平衡。传统的比例克隆不能体现此机制，改进的克隆算子对其进行模拟，克隆规模依据抗体－抗原的亲和力、抗体－抗体的亲和度自适应的调整。为此，先定义抗体i与其它抗体的亲和度Φi见式 （1）

式中：· ——欧式距离，在计算Φi时，对 · 进行归一化处理，即0≤ · ≤1。显然抗体－抗体的亲和度越大，相似度越高，则Φi的值越小，从而抗体间的抑制作用越强。第i个抗体的克隆规模ni，由式 （2）计算

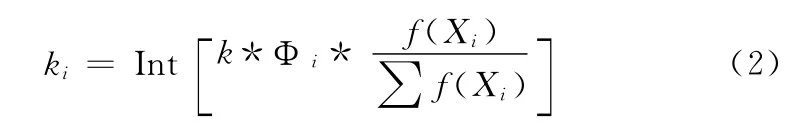
式中：k——抗体群的克隆规模，k＝∑ki，符号Int（·）表示取上整函数。

（2）云自适应变异算子

CLONALG用于求解多峰值问题，变异算子在该算法中显得尤其重要［9］。对克隆扩增后的抗体群中每个抗体进行变异可以提高抗体的多样性，扩大搜索的范围，以用来寻找更优秀的抗体。常见的非一致性变异和高斯变异，具体分别见文献 ［10－11］。

分析非一致性变异和高斯变异可知，非一致性变异虽然随着演化的推进，变异的范围由大到小，由全局搜索得到局部搜索，但是每次只局限于抗体一个分量的微调，则变异操作的效果不明显，群体的多样性不能保证，因而难以收敛于全部峰值；高斯变异能较好地对多个分量实施变异，克服了非一致变异的一些不足，但是未考虑整个抗体群的全局情况，而只是针对样本抗体的状况进行调整。针对此不足，本文借鉴云模型的思想，提出云自适应变异操作。

云模型用期望值Ex、熵En和超熵He表征定性概念，将概念的模糊性和随机性集成在一起，为定性与定量相结合的信息处理提供了有力手段。期望值Ex反应了云层的重心位置；En反应了云层的陡峭程度，En越小越陡峭；超熵He反应了云层的厚度，He越大云层越厚［12－13］，如图1所示。当x＞Ex时，确定度随x的增大而减小，云模型中云滴集中在区间［Ex－3En，Ex＋3En］，具有随机性和稳定倾向。把云模型的这一特征应用于抗体变异的控制。亲和力小的抗体进行较大的变异，以求生成亲和力大的抗体，反之，要求变异较小，以保护优良抗体。云自适应变异算子按照式 （3）操作。

图1 正态云模型的3个数字特征

式中：e、h——控制参数，e用来控制云的陡峭程度，根据“3En”规则，一般去3，h用来控制云层的厚度，一般去10，αi、pc为特定的参数，实验中根据具体情况调整。

（3）抗体重组算子

借鉴遗传算法交叉的思想，引入抗体重组算子。设3个独立的父代抗体s1、s2、s3杂交生成子代抗体sc，其中sc满足式 （4）

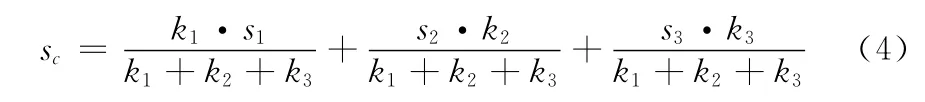
式中：k1、k2、k3——随机生成的3个不全为0的实数。

云自适应变异算子、抗体重组算子的共同作用，既保证了优良抗体基因的遗传，又实现了抗体间的信息交流、协同进化，使得克隆后的抗体群在亲和力高的抗体周围分散开，大大增加了抗体群的多样性，提高算法的收敛速度。

（4）精英抗体保存算子

为减少冗余计算，模拟遗传算法的精英种子保存策略，建立记忆种群，将多个优良抗体直接放在记忆种群中，启发了抗体群收敛的方向，为快速收敛得到全局最优解提供保障。

2.2 算法的步骤

结合FCCSA的设计，下面给出算法的具体执行步骤：

步骤1 随机生成规模为q的初始抗体群X（0）＝｛X1，X2，X3，…Xq｝；

步骤2 精英抗体保存算子：在抗体群X（t）中选择m个适应度最大的抗体，加入记忆种群Xm（t）；

步骤3 克隆算子：对记忆种群Xm（t）依据式 （2）实施克隆，克隆后的抗体群为Xc（t）＝ ｛Xc1，Xc2，Xc3，…Xcq｝，Xci为个体Xi的克隆子群；

步骤4 云自适应变异算子：对抗体群Xc（t）依据式（3）对抗体的每个基因进行云自适应变异，生成抗体群X＊（t）；

步骤5 抗体重组算子：从抗体群Xc（t）中依次选取3个父代抗体s1、s2、s3依据式 （4）进行重组生成子代sc，直到不够选择3个为止，最后生成抗体群Xr（t）。

步骤6 合并抗体群 X＊（t）和 Xr（t），生成抗体群Xl（t）；

步骤7 抗体群更新操作：随机产生d个新抗体，替换抗体群Xl（t）中亲和力较小的抗体；

步骤8 终止判断。若不满足迭代次数，则更新演化代数记数器t→t＋1，并选取抗体群Xl（t）的m个亲和力较大的抗体组成下一代抗体群Xm（t），然后转入到步骤3；否则，输出结果，算法结束。

算法结束后，记忆种群中的抗体即为所求问题的解。

3 仿真分析

为了测试本文提出的FCCSA的效果，对文献 ［14］中的测试函数进行仿真实验，测试函数见表1。其中f1～f5为单峰函数，f6～f10为多峰函数。

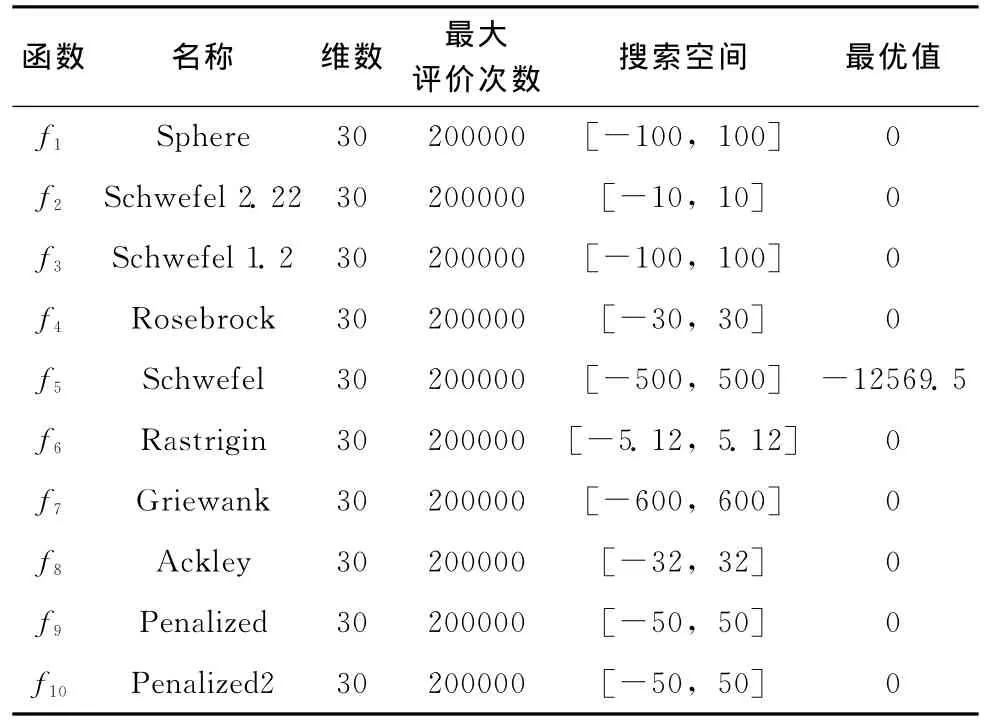
表1 测试函数的相关参数

测 试 环 境：Pentium （R）Dual－Core CPU E5500 2.79GHZ，Windows XP操作系统，Matlab语言编程实现，FCCSA的参数设定如下fccsamax＝300，q＝20，m＝5，k＝60，e＝3，h＝10，pc＝0.8，d＝10，αi＝3，i＝1，2，…，n。与混 沌 克 隆 选 择 算 法［15］（chaos clonal selection algorithm，CCSA）、粒子群克隆选择算法［16］（PSO－CSA）进行比较。mean，std和t分别为算法独立实验20次的平均最优适应值、标准差和平均运行时间，mean显示了在给定的函数评价次数下算法所能达到的精度，反映了算法的收敛速度；std反映了算法的稳定性和鲁棒性；t反映了算法的时间效率。结果见表2。

由表2数据对比可以看出，在10个标准测试函数中，无论算法的收敛精度，还是算法的稳定性，FCCSA都比CCSA和PSO－CSA都有很大的提高；时间效率也较为理想，说明FCCSA寻优能力提高的同时，时间复杂度没有增加。

为了更直观地反映算法的寻优效果，引入文献 ［17］中种群多样性测量指标。种群多样性是指种群中个体的差异性，多样性缺失的直接结果就是搜索就可能陷入一个不含全局最优点的区域难以逃离，这就是早熟问题。种群多样性定义见式 （5）

式中：f（Am，n）avg、f（Am，n）max——当代种群个体的平均适应度值、最大适应度值。PDM ∈［0，1］，当算法收敛时，其值趋于1。

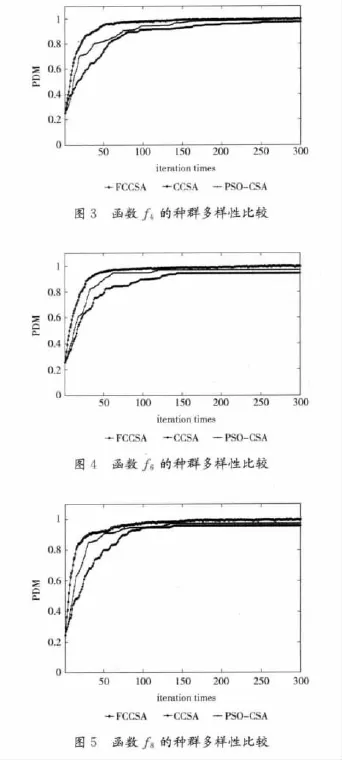
对相关测试函数的种群多样性比较如图2～图5，其中横坐标表示迭代次数，纵坐标表示种群多样性指标PDM。

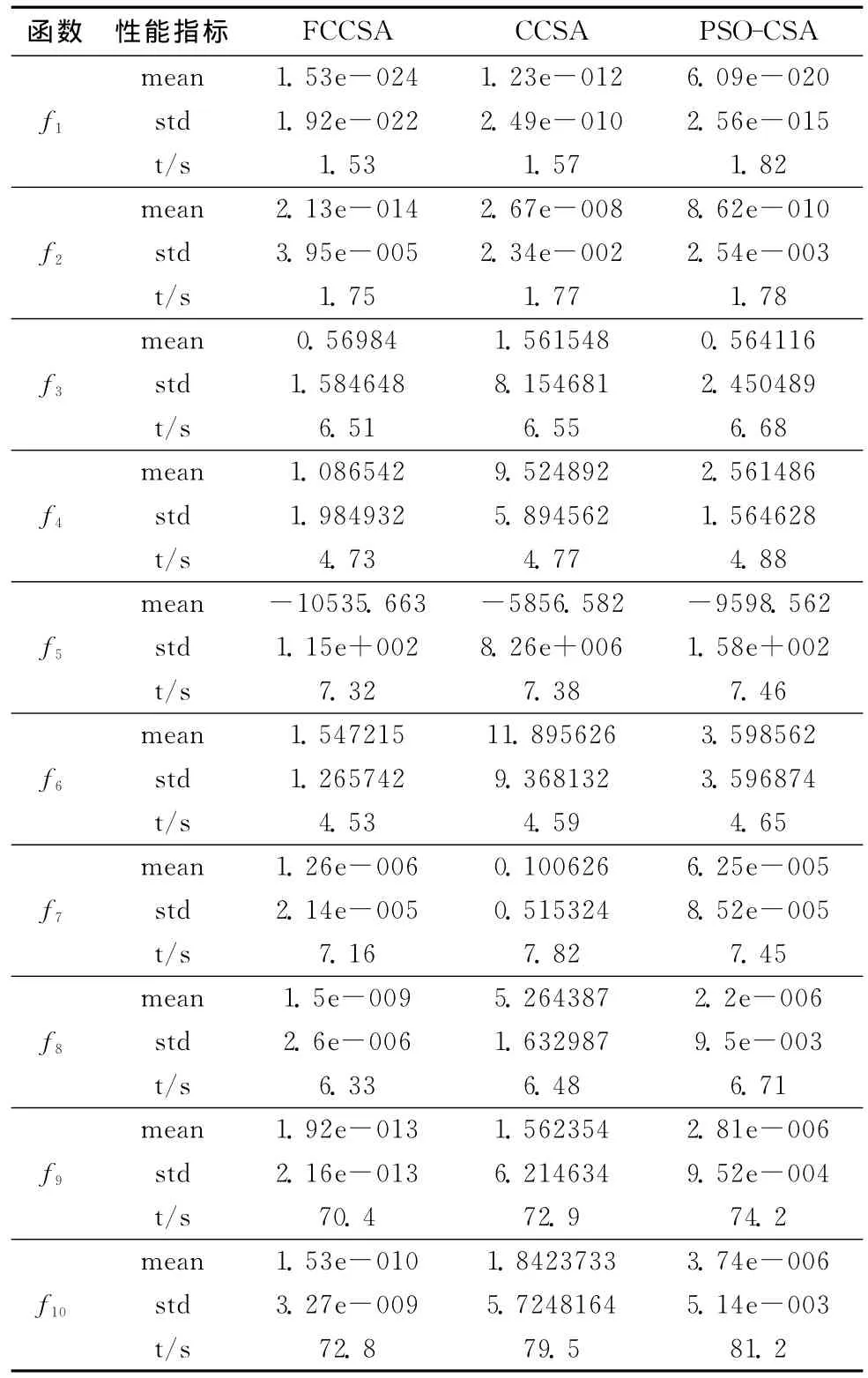
表2 测试函数基于3种算法的计算结果比较

图2 函数f2的种群多样性比较

图2、图3可直观看出，对于单峰函数，FCCSA的收敛速度明显较CCSA和PSO－CSA快，寻优能力与PSOCSA差不多；图4、图5可直观看出，对于多峰函数，对比CCSA和PSO－CSA，FCCSA不仅收敛速度优势突出且全局寻优能力有很大的提高，这是因为新型克隆算子、云自适应变异算子和抗体重组算子大大增加了种群的多样性，使得FCCSA具有很强的全局和局部搜索能力。

4 结束语

针对CLONALG种群多样性少，容易早熟的缺陷，本文借鉴免疫调节机制，引入新型克隆算子，有效扩充优良抗体和抑制相似抗体，维持了免疫平衡；结合云模型在“3En”区间的随机性和稳定倾向性，提出云自适应变异，与抗体重组算子合作在克隆的基础上实现了父代抗体周围多个方向进行全局和局部进化。仿真实验进一步表明，与CCSA和PSO－CSA相比，本文提出的FCCSA的寻优能力、鲁棒性性能显著提高，同时时间复杂度不高，是一种解决函数优化问题较优秀的群智能优化算法。下一步，重点研究FCCSA在特定实际问题中的应用。

［1］MA Chunhua，ZHONG Yong.Dynamic adaptive immune clone selection algorithm by applying population division ［J］.Computer Engineering and Applications，2011，47 （30）：29－31 （in Chinese）.［马春华，钟勇.采用种群划分的动态自适应免疫克隆选择算法 ［J］.计算机工程与应用，2011，47 （30）：29－31.］

［2］TAO Xinmin，LIU Yu，FU Dandan，et al.Hybrid mutation clonal selection multiobjective optimization algorithm ［J］.Computer Simulation，2011，28 （10）：199－203 （in Chinese）.［陶新民，刘玉，付丹丹，等.混合变异克隆选择多目标优化算法 ［J］.计算机仿真，2011，28 （10）：199－203.］

［3］YE Hongtao.Wastewater treatment system predicting and optimization control based on immune algorithm ［D］.Guangzhou：South China University of Technology，2011：44－46 （in Chinese）.［叶洪涛.基于免疫算法的污水处理系统预测及优化控制研究 ［D］.广州.华南理工大学，2011：44－46.］

［4］WU Zengwei，CHEN Sicheng，GU Jinguang.Paralleling clonal selection algorithm with OpenMP ［J］.Journal of Wuhan University of Technology （Information ＆ Management Engineering），2011，33 （6）：920－923 （in Chinese）. ［吴增伟，陈思成，顾进广.基于OpenMP的并行克隆选择算法 ［J］.武汉理 工 大 学 学 报－信 息 与 管 理 工 程 版，2011，33 （6）：920－923.］

［5］Dai Hongwei，Yang Yu，Li Cunhua.Improved quantum crossover based clonal selection algorithm ［C］／／3rd International Conference on Intelligent Networks and Intelligent Systems，2010：366－369.

［6］CHEN Lin，YAO Hongliang.Application of immune clonal genetic algorithm on logistics and distribution ［J］.Journal of Henan Institute of Science and Technology （Engneering Science），2012，40 （5）：70－74 （in Chinese）. ［陈林，姚宏亮.免疫克隆遗传算法在物流配送中的应用 ［J］.河南科技学院学报：自然科学版，2012，40 （5）：70－74.］

［7］LIU Qiong，WU Xiaojun.An improved immune clonal selection algorithm ［J］.Journal of Shandong University （Engineering Science），2009，39 （6）：8－12 （in Chinese）. ［刘琼，吴小俊.一种改进的免疫克隆选择算法 ［J］.山东大学学报 （工学版），2009，39 （6）：8－12.］

［8］QIAN Hai，MA Jianhui，WANG Xufa.New artificial immune algorithm based on the clonal selection principle ［J］.Journal of University of Science and Technology of China，2008，38（12）：1397－1406 （in Chinese）. ［钱海，马建辉，王煦法.一种新的基于克隆选择原理的人工免疫算法 ［J］.中国科技大学学报，2008，38 （12）：1397－1406.］

［9］Paw J K S，Chong Kok Hen，Koo Wai Yan，et al.Improved combined mutation clonal selection algorithm ［C］／／IEEE Conference on Sustainable Utilization and Development in Engineering and Technology，2012：92－196.

［10］Dai Yugang，Liu Zhandong.An almost everywhere strong convergence analysis for clonal selection algorithm ［C］／／International Conference on Computer Design and Applications，2010：108－111.

［11］HAN Xuming.Some improved artificial immune algorithms and their applications in the field of atmospheric environment［D］.Changchun：Jilin University，2010：23－25 （in Chinese）.［韩旭明.若干改进的人工免疫算法及其在大气环境领域中的应用 ［D］.长春.吉林大学，2010：23－25.］

［12］WANG Hongli.Qualitative modeling of complex system based on cloud model using QSIM ［J］.Application Research of Computers，2012，29 （12）：4593－4597 （in Chinese）. ［王洪利.基于云模型以约束为中心的复杂系统定性建模 ［J］.计算机应用研究，2012，29 （12）：4593－4597.］

［13］DONG Lili，GONG Guanghong，LI Ni，et al.Adaptive parallelh simulated annealing genetic algorithms based on cloud models ［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37 （9）：1132－1136 （in Chinese）. ［董丽丽，龚光红，李妮，等.基于云模型的自适应并行模拟退火遗传算法 ［J］.北京航空航天大学学报，2011，37 （9）：1132－1136.］

［14］Yao X，Liu G.Evolutionary programming made faster ［J］.IEEE Trans on Evolutionary Computation，1999，3 （2）：82－102.

［15］HONG Lu，JI Zhicheng，GONG Chenglong.On convergence rate of chaos clonal selection algorithm ［J］.Journal of Sytem Simulation，2011，23 （10）：2060－2064 （in Chinese）. ［洪露，纪志成，龚成龙.混沌克隆选择算法及其收敛速度分析［J］.系统仿真学报，2011，23 （10）：2060－2064.］

［16］WANG Qiaoling.Research of hybrid optimization algorithms based on swarm intelligence ［D］.Harbin：Harbin Institute of Technology Press，2010：23－25 （in Chinese）. ［王巧灵.基于群体智能混合优化算法的研究 ［D］.哈尔滨：哈尔滨工业大学出版社，2010：23－25.］

［17］WANG Guangyuan，JI Wanfeng，SUN Junzheng，et al.The fire distribution for shore－based missiles based on improved particle swarm optimization ［J］.Aerospace Control，2012，30 （5）：71－77 （in Chinese）. ［王光源，汲万峰，孙钧正，等.基于改进PSO算法的岸基导弹火力分配研究 ［J］.航天控制，2012，30 （5）：71－77.］