初应力对压电薄膜体声波谐振器厚度拉伸模态谐振特性的影响

黄德进，王 骥，罗昕逸

(宁波大学 机械工程和力学学院，宁波 315211)

在通讯、导航、计算机技术和医疗设备等电子行业中，谐振器是不可或缺的频率器件。最近十几年发展起来的压电薄膜体声波谐振器(FBAR)［1-3］具有传统的陶瓷介质谐振器和声表面波谐振器的优点，同时又克服两者的缺点，其工作频率高(600MHz～20GHz)、温度系数小、容量大、体积小和成本低。更重要的是，FBAR可以制作在陶瓷、硅片等基体上。其制作工艺能与半导体工艺兼容，是可以和射频集成电路(RFIC)或单片微波集成电路(MMIC)集成的谐振器［4-5］。符合现代电子器件发展的方向，具有广阔的发展前途。

FBAR是一种具有电极层、压电层和支撑层等组成的层合结构。在器件制作过程中，由于多层结构中相邻层材料的力学和热学性能之间的差异，结构中会不可避免地产生初应力;另外，对于PZT陶瓷等脆性薄膜，为了防止其脆性断裂往往要人为地使薄膜中存在预压应力。在薄膜体声波器件设计和优化中，常采用Mason模型和BVD模型效电路法，也采用解析法来研究［6-11］。迄今为止，还未见FBAR谐振特性受初始应力影响的研究工作报道。本文研究了初应力对理想FBAR在厚度拉伸模态下谐振特性的影响，讨论了串联和并联谐振频率、带宽、机电耦合系数等重要参数与初应力之间的关系。并给出了数值算例。

1 基本方程和问题的解

本文研究的理想FBAR由一层压电薄膜夹于两层极薄的导体之间，导体的厚度、质量和刚度均可以忽略不计，并设压电层中的初应力为常数。FBAR的厚度尺寸为2b，远小于长度l和宽度w，因此可以作为厚度方向的一维问题来处理。FBAR的几何尺寸和坐标系如图1所示。

含初应力的压电弹性体三维运动方程［12］和电荷方程分别为:

图1 FBAR的几何尺寸和坐标系Fig.1 The FBAR geometry and coordinate system

式中:Tij、ui、Di分别为应力、位移和电位移，表示初应力，ρ是密度，是位移对时间t的二阶导数，i，j，k=1，2，3。应变Sij和位移关系以及电场强度Ei与电势φ之间的关系分别为，

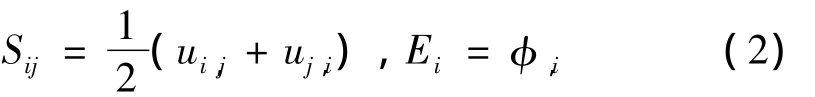
压电材料的本构关系采用第四类压电方程:

在厚度拉伸模态下，假设位移为:

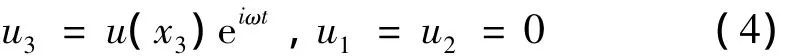
式中:u(x3)为待定的表达式。这样应变为:

这样，FBAR的本构方程、运动方程和电荷方程分别简化为:

将式(6)代入式(8)，并利用式(2)1和(9)，可得:

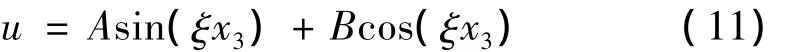
式中:A、B为待定常数，ξ为波数:

FBAR谐振时，由式(9)可得:

式中:D为常数。将式(11)、(13)代入(3)1，并注意到式(5)2，可得:

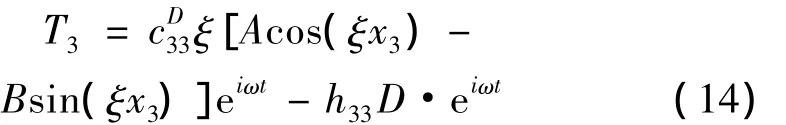
在谐振器质心处，x3=0，u=0，代入式(11)可得B=0。FBAR上下表面为自由，其边界条件为:

将式(14)代入(15)，可得:

将式(16)和B=0代入式(11)可得位移，由式(7)可得电场强度:

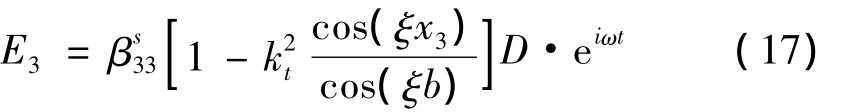
式中:S为电极的面积。这样FBAR厚度拉伸振动时的电阻抗可由式(18)和(19)得到:

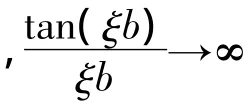
再利用式(12)，可得:

当阻抗为零时，此时的谐振频率为串联谐振频率fs。由式(20)可知:

由式(23)可解得串联谐振频率fs。串联谐振频率与并联谐振频率之差为谐振器的带宽。带宽可以用下式近似来计算:

FBAR的有效机电耦合系数［13］为:

2 数值算例和讨论

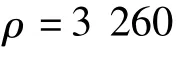
图2 不同初应力下的FBAR阻抗特性Fig.2 The impedance characteristics of FBAR under different initial stresses

图2是理想FBAR的阻抗幅值、相位特性与初应力的关系图。可以看出，无初始应力时，其基波串联谐振频率为2.768 GHz，基波并联谐振频率为 2.839 GHz，带宽为69.2 MHz，有效机电耦合系数为0.058 7。随着初应力的增加，串联谐振频率和并联谐振频率也会提高。谐振频率与初应力的关系可以进一步由图3给出。由式(22)可知，并联谐振-初应力曲线为抛物线，但曲线弧度不大，可用直线近似代替:

式中:fp0为初应力为零时的并联谐振频率。带宽与初应力之间的关系由图4给出。也是随着初应力的增加，带宽越来越大，也近似线性关系。图5为有效机电耦合系数随初应力的变化。有效机电耦合系数基本保持一个常数，与初应力的变化没有什么关系。

3 结论

本文研究了含初应力的理想压电薄膜体声波谐振的振动，给出了阻抗的表达式，讨论了串联谐振频率、并联谐振频率与初应力之间的关系，也讨论了初应力对带宽和有效机电耦合系数影响。通过推导发现，在各初应力分量中，只有拉伸应力分量会对FBAR厚度拉伸模态的谐振产生影响，其它分量不起作用。给出的数值算例表明，初应力会提高谐振频率和带宽，初应力与频率、带宽的关系可近似为线性关系。初应力对机电耦合系数基本没有影响。

图3 FBAR谐振频率与初应力之间的关系Fig.3 The relationship between frequency and initial stress

图4 FBAR带宽与初应力之间的关系Fig.4 The relationship between bandwidth and initial stress

图5 有效机电耦合系数与初应力之间的关系Fig.5 The relationship between effective electro-mechanical coupling coefficientand initial stress

［1］ Lakin K M，Wang J S.Acoustic bulk wave composite resonators［J］.Applied Physics Letters 1981，39(3):125-128.

［2］ Krishnaswamy S V，Rosenbaum J，Horwitz S，et al.Film bulk acoustic wave resonator technology［C］.IEEE Ultrason Symposium，1990，1(1):529-536.

［3］ Lakin K M.A review of thin-film resonator technology［J］.IEEE Microwave Magazine，2003，4(4):333-336.

［4］ Bradley P，Ruby R，Larson J D，et al.A film bulk acoustic resonator(FBAR)duplexer for USPCS handset applications［J］.Microwave Symposium Digest，2001，1(1):367-370.

［5］Aigner R.High performance RF-filters suitable for above IC integration:film bulk-acoustic-resonators(FBAR)on silicon［C］.IEEE Custom Integrated Circuits Confrence，2003，1(1):141-146.

［6］Huang，D J，Wang J，Du J K.The analysis of high frequency vibrations of layered anisotropic plates for FBAR application［C］. 2008 IEEE International Frequency Control Symposium，2008:204-208.

［7］Wang J，Liu J S，Du J K，et al.The calculation of electrical parameters offilm bulk acoustic wave resonatorsfrom vibrations of layered piezoelectric structures［C］.Proceedings of the 2009 IEEE International Ultrasonics Symposium，2009:2027-2030.

［8］Wang J，Liu J S，Du J K，et al.The analysis of film acoustic wave resonators with the consideration of film piezoelectric properties［C］.2nd International Conference on Smart Materials and Nanotechnology in Engineering，2009:388-391.

［9］ Wang J，Liu J S，Du J K，et al.The calculation of quality factor of film bulk acoustic resonators with the consideration of viscosity［C］.Proceedings of the Joint Conference of the 2009 Symposium on Piezoelectricity，Acoustic Waves，and Device Applications and China Symposium on Frequency Control Technology，2009:370-375.

［10］ Huang D J，Wang J.Analysis of the vibration of film bulk acoustic wave resonators based on Mindlin plate theory［C］.Symposium on Piezoelectricity，Acoustic Waves，and Device Applications，2011:328-331.

［11］ Huang D J，Wang J.Vibration analysis of layered film bulk acoustic resonators based on Mindlin plate theory［C］.Symposium on Piezoelectricity，Acoustic Waves，and Device Applications，2010:485-478.

［12］ Biot M A.Mechanics of incremental deformations［M］.John Wiley ＆ Sons，Inc，New York，1964.

［13］ Lakin K M，Kline G R，McCarron K T.High-Q micromicrowave acoustic resonators and filters［J］. IEEE Transactions on Microwave Theory and Techniques，1993，41(12):2139-2146.