下击暴流空间相关性风场模拟

张文福，谢 丹，刘迎春，计 静

(1.东北石油大学 土木建筑工程学院，大庆 163318;2.黑龙江省防灾减灾及防护工程重点实验室，大庆 163318)

下击暴流风速是自然界中的极端风荷载的来源之一，已引起世界各地许多结构的破坏［1-2］。Fujita［3］将下击暴流风速定义为一股强烈的下沉气流引起的沿着地面或靠近地面的极具破坏力的爆发性强风。Chay等［4］从本质上详细的阐述了下击暴流风速的形成方式。

国外许多学者通过风场实测、风洞实验模拟、CFD数值模拟等方法对下击暴流风速进行大量研究，提出了一些下击暴流风速的竖向风剖面和水平径向风剖面的数学模型［5-8］。Chen等［9］在这些数学模型的基础上提出了一种下击暴流风速数值模拟的模型，即:确定性-随机性混合模型(Deterministic-Stochastic Hybrid model，本文简称为 DESH 模型)。瞿伟廉等［10］在DESH模型的基础上采用改进的谐波叠加法对下击暴流风速进行数值模拟研究;潘峰等［11］采用DESH模型模拟了跨度屋盖结构的下击暴流风场，并对其进行了边界层风洞试验研究。王昕等［12］在DESH模型的基础上联合运用FFT算法和谐波叠加法模拟了下击暴流风速的脉动成分，并对下击暴流风荷载作用下高耸输电塔进行风振响应研究。李春祥等［13］采用DESH模型对某一固定位置处的竖向分布下击暴流风场进行了数值模拟，并且在模拟随机脉动成分时引入了三次样条函数插值技术，提高了下击暴流风场数值模拟的效率。

由于目前实测的下击暴流风速曲线记录比较少，因此在现有的数学模型基础上开展下击暴流风场的数值模拟研究显得十分必要。本文在Chen等［9］提出的DESH模型的基础上，利用Wood［7］竖向风剖面模型和Holmes［8］水平径向风剖面模型模拟出空间各点处的平均风速，并采用AR模型生成具有时间相关性和空间相关性的脉动风速，从而模拟得到下击暴流空间相关性风场。

1 DESH模型

在这个模型中，空间各点的下击暴流风速由具有确定性的平均风和具有随机性的脉动风两部分组成，M个空间点的风速时程向量(风场)V(x，y，z，t)=［V1(x1，y1，z1，t)V2(x2，y2，z2，t)…VM(xM，yM，zM，t)］T中任意一点可表示成:

式中:Vi(xi，yi，zi，t)是关于空间中一点同风暴中心相对位置坐标xi，yi，zi和时间t的函数，表示随时间变化的平均风速，可以由一个确定的函数来指定，称为具有确定性的平均风;vi(xi，yi，zi，t)是与风暴中心相对位置有关的零均值的脉动风，是一个随机过程。

在不影响工程精度要求的前提下，对DESH模型作如下假定:① 各位置处平均风速的最大值在时间函数取得最大值时获得;② 非平稳的脉动风可以通过一个平稳随机风速场进行幅度调制来获得;③ Davenport提出的脉动风相干函数适用于DESH模型。

1.1 平均风速

空间中一点任意时刻t的平均风速可以用一个竖向风剖面函数与一个时间函数的乘积来表示，即:

式中:Vi(zi)为最大平均风速的竖向风剖面;fi(xi，yi，t)为描述竖向风剖面随时间变化的函数，其最大值为1;xi，yi为空间点相对风暴中心的位置坐标。

对于竖向风剖面，本文采用 Wood等［7］提出的模型，其表达式为:

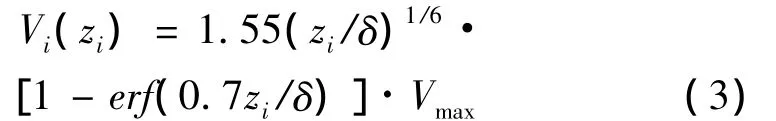
式中:zi为空间点距地面的高度;Vmax为最大风速;δ为高度参数，它等于取得最大风速Vmax时离地面高度的一半;erf是容许误差函数，其表达式为:

Holmes在前人研究的基础上提出考虑时间衰减性的径向射流速度分布规律及风暴移动速度的概念，并指出:空间点任意时刻的平均风速Vci(xi，yi，t)等于下击暴流径向射流速度Vri(xi，yi，t)与风暴中心移动速度Vt的矢量和:

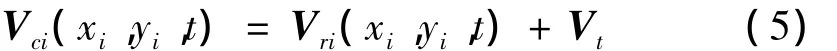
其中径向射流速度通过下式确定:

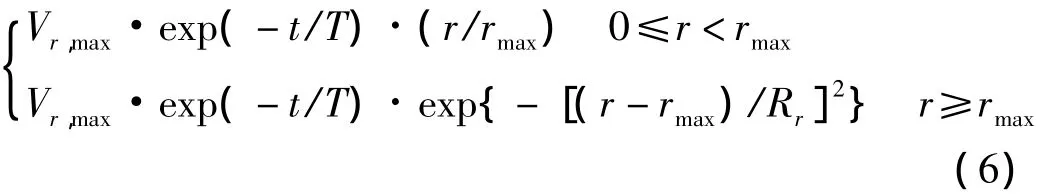
式中:r为t时刻空间点与风暴中心点的距离;Vr，max为最大的径向射流速度;rmax为取得Vr，max时的位置距风暴中心的径向距离;Rr为径向的特征距离;T为下击暴流持续时间。

假设风暴中心沿X方向移动，风暴中心与空间点的位置关系及速度关系图如图1所示。分析图1可知，假设在XOY坐标系中:0时刻风暴中心点O坐标为(0，0)，空间点P坐标为(xi，yi);在X'O'Y'坐标系中:t时刻风暴中心点O'坐标为(0，0)，空间点P'坐标为(x，y)。则:

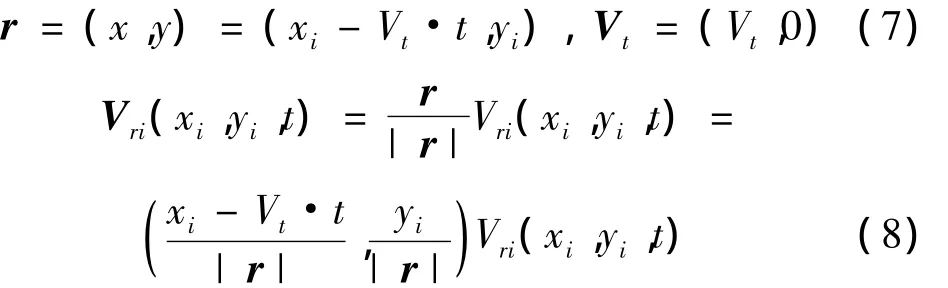
将式(7)和式(8)代入式(5)得:

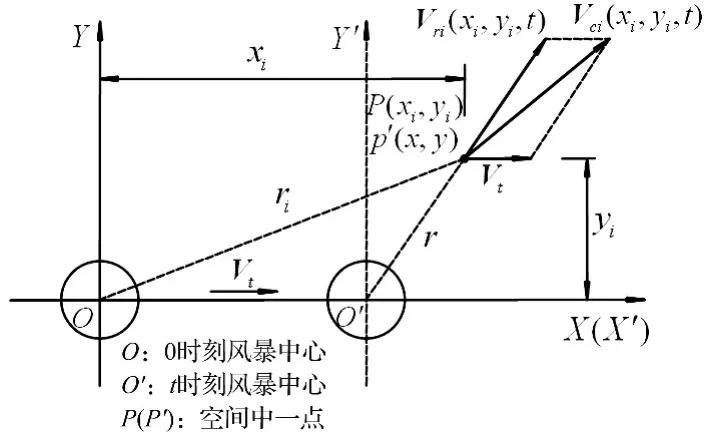
图1 径向速度与风暴移动速度矢量合成图Fig.1 Vector combination of radial and translation

将式(9)代入式(4)即可求出时间函数，再将式(4)代入式(2)可求得随时间变化的平均风速。从中可以看出平均风速与空间点P相对于0时刻风暴中心的坐标(xi，yi)及离地面高度zi有关，图2给出了空间四点的平均风速随时间的分布情况，其中0时刻风暴中心的坐标为(0，0)，沿X轴方向以12 m/s的速度移动，空间四个点的坐标分别为P1(2 000，100，20)、P2(4 000，100，40)、P3(3 000，150，60)、P4(3 000，50，80)，风暴中心与空间点的位置关系如图1所示。

1.2 脉动风速

下击暴流风速的脉动风部分是一个非平稳的随机过程，可以通过一个平稳随机风速场进行幅度调制来获得:

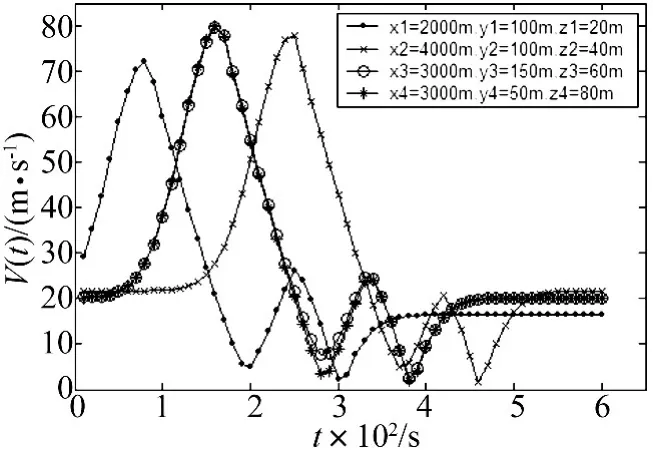
图2 空间四点平均风速分布图Fig.2 Average wind speed distribution of 4 spatial points

由于ki(xi，yi，zi，t)服从风速谱的频谱分布特性，本文采用Davenport单边风速谱，归一化后的结果为:

下面讨论ki(xi，yi，zi，t)的生成。生成脉动风的模型包括 AR模型、小波分析模型、谐波叠加模型等［15-16］。与谐波叠加模型相比，AR模型的计算量小、速度快，模拟的效率较高［17-18］，尤其是在生成一系列具有空间相关性脉动风速时，AR模型的效率远高于谐波叠加模型［15］。当然，谐波叠加模型数学基础严密，在模型的精度上略高于AR模型，但是从后文中相关函数及功率谱的对比可以看出，AR模型的模拟结果也能满足工程精度的要求。小波分析模型虽然精度也较高，但是其程序特别复杂，计算效率也低于AR模型。

本文利用文献［15］中的标量AR模型产生一系列具有时间相关性，但是在空间上互不相关的脉动风速ui(t)，i=1，2，…，M，之后在考虑各个点之间的空间相关性，从而模拟出下击暴流空间相关性脉动风速。

1.2.1ui(t)的生成

P阶AR 模型为［15］:

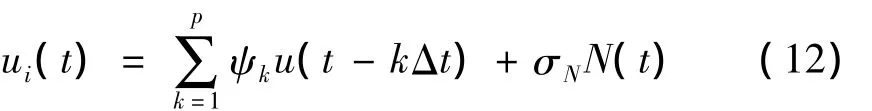
式中:p为自回归阶数，ψk为自回归系数，N(t)为均值为0、方差为1的正态分布随机数。

依次将式(12)两边都乘以ui(t-jΔt)和ui(t)并取数学期望得［15］:

其中Ru(jΔt)是风速时间序列的自相关函数，根据维纳-辛钦公式得到自相关函数可由下式来计算:

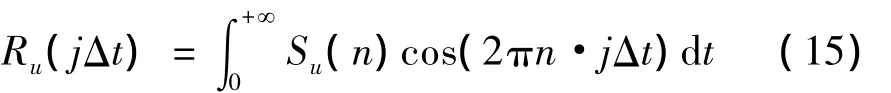
1.2.2 空间相关性脉动风速的产生

ui(t)向具有特定相关特性脉动风速ki(xi，yi，zi，t)，i=1，2，…，M的转化可通过下式:

C为一个下三角矩阵，其元素可用如下递推公式求得:

其中:R0为脉动风的互相关函数，可由下式求得:

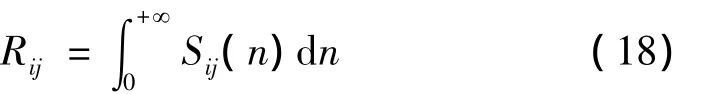
式中:Sij(n)为i点与j点的互功率谱密度，可由自功率谱密度和相干函数确定，如式(19)和式(20)所示［15-16］:

式中:Cx、Cy、Cz分别为空间任意两点左右、上下、前后的衰减系数)分别为第i点与第j点的平均风速，取零时刻的值;(xi，yi，zi)、(xj，yj，zj)分别为空间i，j点的三维坐标。

2 算例

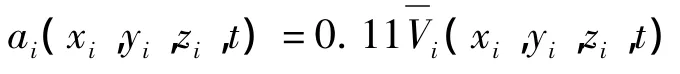
图3 空间七点坐标Fig.3 Coordinates of 7 spatial points

图4 空间七点的风速时程曲线Fig.4 Wind velocity history samples of 7 spatial point

表1 下击暴流风场模拟时的主要参数Tab.1 Main parameters of downburst wind field simulation

图5 相关函数的对比Fig.5 Comparisons of correlation function

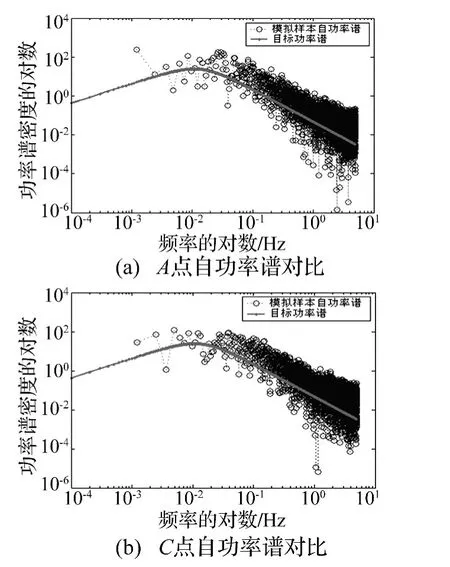
图6 自功率谱的对比Fig.6 Comparisons of auto PSD

3 结论

(1)考虑时间衰减性研究了平均风速与空间观测点相对于零时刻风暴中心的坐标及离地面高度的关系，并给出了空间中四个点的平均风速随时间的分布情况。

(2)在确定性-随机性混合模型的基础上，利用Wood竖向风剖面模型和Holmes水平径向风剖面模型模拟出空间七点处的平均风速，并采用AR模型生成具有时间相关性和空间相关性的脉动风速，从而获得下击暴流空间相关性风场。通过脉动风相关函数及功率谱的对比表明，本文方法具有较高的精度。

由于风暴中心的移动性，空间点的平均风速随时间改变，本文在互相关函数计算中平均风速取零时刻的值来代替，没有考虑其随着时间的变化性，在后续研究中应将风暴中心的移动速度引入相关函数对比中。

［1］HawesH， Dempsey D. Review ofrecentAustralian transmission line failures due to high intensity winds［R］.Paper Presented at Workshop on High Intensity Winds on Transmission Lines，Buenos Aires，Argentina，1993，4:19-23.

［2］Holmes J D.Modeling of extreme thunderstorm winds for wind loading of structures and risk assessment［C］ //Wind Engineering into 21st Century，Proceedings of 10th International Conference on Wind Engineering，Balkema，Rotterdam，1999，2:1409-1415.

［3］Fujita T T.The downburst:Microburst and macroburst:report of projects NIMROD and JAWS［R］.University of Chicago，1985.

［4］Chay M T，Letchford C W.Pressure distributions on a cube in a simulated thunderstorm downburst-Part A:Stationary downburst observations［J］.Journal of Wind Engineering and Industrial Aerodynamics 2002，90:711-732.

［5］Oseguera R M，Bowles R L.A simple analytic 3-dimensional downburst model based on boundary layer stagnation flow［R］.［S.l.］:Langley Research Center，1988.

［6］Vicroy D D.Assessment of microburst models for downdraft estimation［J］.Journal of Aircraft，1992，29:1043-1048.

［7］Wood G S，Kwok K C S，Motteram N A，et al.Physical and numerical modelling of thunderstorm downbursts［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89(6):535-552.

［8］Holmes J D，Oliver S E.An empirical model of a downburst［J］.Engineering Structures，2000，22:1167-1172.

［9］Chen L，Letchford C W.A deterministic-stochastic hybrid model of downbursts and its impact on a cantilever structure［J］.Engineering Structures，2004，26:619-626.

［10］瞿伟廉，王锦文.下击暴流风荷载的数值模拟［J］.武汉理工大学学报，2008，30(2):70-74.QU Wei-lian， WANG Jin-wen. Numerical simulation of downburst wind loads［J］.Journal of Wuhan University of Technology，2008，30(2):70-74.

［11］潘 峰，孙炳楠，楼文娟，等.冲击风作用下大跨屋盖多模态随机风致响应研究［J］.空气动力学学报，2008，26(1):119-125.

PAN Feng，SUN Bin-nan，LOU Wen-juan，et al.Random wind-induced dynamic response of long-span roof to thunderstorm downbursts in the time domain［J］.Acta Aerodynamica Sinica，2008，26(1):119-125.

［12］王 昕，楼文娟，李宏男，等.雷暴冲击风作用下高耸输电塔风振响应［J］.浙江大学学报，2009，43(8):1520-1525.

WANG Xin，LOU Wen-juan，LI Hong-nan，et al.Windinduced dynamic response of high-rise transmission tower under downburstwind load［J］. JournalofZhejiang University，2009，43(8):1520-1525.

［13］李春祥，刘晨哲，申建红，等.土木工程下击暴流风速数值模拟的研究［J］.振动与冲击，2010，29(12):50-54.

LI Chun-xiang，LIU Chen-zhe， SHEN Jian-hong，et al.Numerical simulations of downburst wind speeds in civil engineering［J］.Journal of Vibration and Shock，2010，29(12):50-54.

［14］ Chay M T.Physical modeling of thunderstorm downbursts for wind engineering applications［D］.Lubbock:Texas Tech University，2001.

［15］张文福，马昌恒.两种AR模型空间相干性风场的比较［J］.空间结构，2009，15(2):22-26.

ZHANG Wen-fu，MA Chang-heng.Comparison of two kinds of AR models for spatial correlation wind field simulation［J］.Spatial Structures，2009，15(2):22-26.

［16］张文福，马昌恒，孙晓刚，等.基于小波分析空间相关性风场模拟［J］.空气动力学学报，2008，26(4):425-429.

ZHANG Wen-fu，MA Chang-heng，SUN Xiao-gang，et al.Simulation of wind field with spatial correlation based on wavelet analysis method［J］.Acta Aerodynamica Sinica，2008，26(4):425-429.

［17］马 骏，周 岱，李 磊，等.风时程模拟的高效高精度混合法［J］.工程力学，2009，26(2):53-77.MA Jun，ZHOU Dai，LI Lei，et al.The composite approach for wind time series simulation［J］.Engineering Mechanics，2009，26(2):53-57.

［18］ 李 峰，窦 鹏，王 磊.风荷载模拟方法探讨［J］.水利与建筑工程学报，2009，7(4):57-59.

LI Feng，DOU Peng，WANG Lei.Discussion on numerical simulation methods of wind load［J］.Journal of Water Resources and Architectural Engineering，2009，7(4):57-59.