新一代冲击加速度国家基准装置的研究与建立
于 梅,胡红波,左爱斌,杨丽峰,刘爱东
(中国计量科学研究院,北京 100013)
研究建立新一代冲击加速度国家计量基准装置是为了解决冲击加速度量值准确溯源问题,它对解决航空航天、国防兵器、交通船舶、建筑工程、核动力、地质物探等众多领域的结构动力学设计、设备安全运行、新产品研发、环境保护及生命科学等问题均具有重要的理论研究和实际应用价值。
随着高新技术和国家重大工程以及国防建设的快速发展,相关领域对冲击计量基标准和测量技术提出了更新、更高的需求,国际上先进国家的冲击计量标准都进行了相应技术提升。引领国际振动与冲击校准领域发展方向、代表国际最高水平的德国物理技术研究院(PTB)现有国家冲击加速度标准装置两项,均采用ISO 16063-13“激光干涉法冲击绝对校准”的外差式激光多普勒技术复现冲击加速度量值[1],其中低g值冲击标准装置的加速度峰值50~5 000 m/s2,冲击脉宽1~10 ms,冲击灵敏度测量结果的扩展不确定度为0.5%(k=2)。高g值冲击标准装置由三根Hopkinson杆组成,其加速度峰值1 000~100 000 m/s2,冲击脉宽30~300 μs,冲击灵敏度测量结果的扩展不确定度为1%(k=2)[2-4]。
原保存在中国计量科学研究院的国家冲击基准有两项,4×102~2.5×104m/s2冲击加速度基准采用落锤式激励的冲击力法(对应的国际标准“废止”);2.5×104~1×105m/s2冲击加速度基准装置为空气炮式激励的CO2法激光测速法。由于测量技术和方法落后、装置扩展不确定度[3% ~5%(k=2)]大,该基准已远不能满足国内量值溯源的需要,并严重制约了冲击测量技术的发展。中国计量科学研究院研究建立的新一代冲击加速度激光绝对法基准装置采用国际最新测量方法,在冲击加速度峰值20~1 000 000 m/s2和脉冲持续时间20~200 μs范围内,实现了加速度计冲击灵敏度的绝对法校准。装置拓展了ISO 16063-13国际标准规定的冲击加速度峰值绝对法测量范围,测量结果的不确定度在可比范围内(200~100 000 m/s2)满足国际标准的要求。
1 装置的构成
冲击加速度基准主要由冲击激励系统(包括冲击激励源、产生冲击信号的Hopkinson杆和垫层)、激光测量系统(包括激光干涉仪、信号调理单元、数据采集处理系统)组成,高冲击装置和中小冲击装置结构原理图如图1、图2所示。
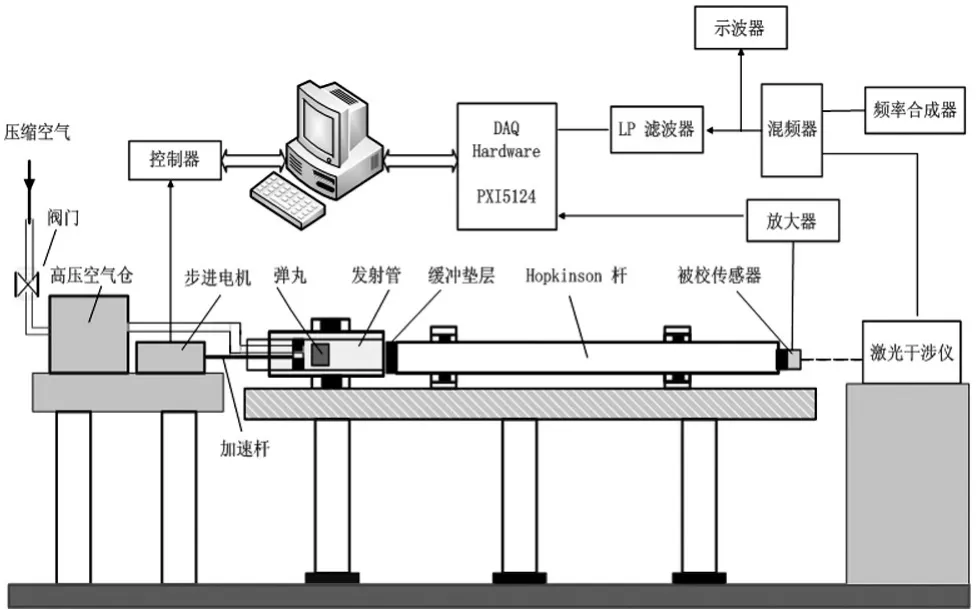
图1 高冲击装置结构原理图Fig.1 Diagram of high shock device
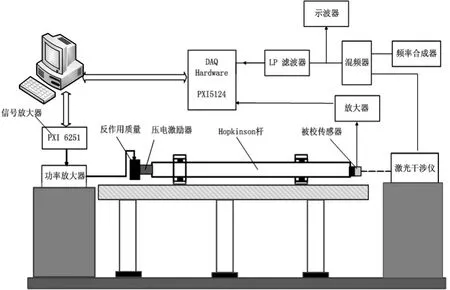
图2 中小冲击装置结构原理图Fig.2 Diagram of small-medium shock device
高冲击装置的激励系统由高压气室、电磁控制单元、步进电机、加速管、弹丸、垫层和Hopkinson杆组成。通过步进电机控制加速杆位置,当弹丸在加速管中被加速,撞击安装有缓冲垫层的Hopkinson杆的一端后,撞击产生的应力波沿杆传递并在杆的另一端反射从而产生冲击加速度波形[5]。中小冲击装置的冲击激励源由压电叠堆激励器、反作用质量块、功率放大器和Hopkinson杆等组成,利用压电晶体的逆压电效应(即轴向极化的压电陶瓷叠堆在交变电场中产生轴向交变形变),给压电叠堆激励器输入一经功率放大器放大后的给定信号,此时压电叠堆产生形变而作用于Hopkinson杆的一端从而产生与机械碰撞一样的应力波。
利用自主研制的外差激光干涉仪测量Hopkinson杆安装被测传感器端面的位移。采用虚拟仪器技术,利用NI的PXI仪器模块和LabView图形化软件平台,编制冲击数据采集处理软件,构建冲击加速度激光绝对法测量系统。采集卡同步采集激光干涉信号与被校传感器的输出信号,测量软件完成信号的分析及处理,从而实现冲击加速度峰值、脉宽持续时间和冲击灵敏度的绝对法测量。
2 解决的关键技术
2.1 冲击激励系统
高冲击采用德国SPEKTRA公司生产的CS18PHS高精度冲击激励器,可输出冲击加速度峰值5 000~1 000 000 m/s2、脉冲持续时间 20 ~200 μs的冲击加速度。通过编制高冲击激励驱动控制软件,构建了高冲击激励控制系统。该装置产生类正弦(一个周期)的冲击加速度波形,见图3。
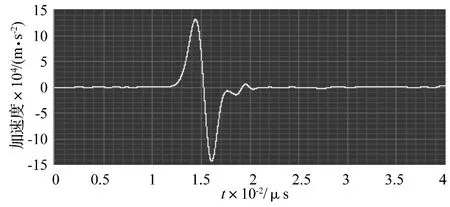
图3 高冲击系统输出的冲击加速度波形Fig.3 Acceleration waveform of high shock system output
中小冲击采用压电叠堆激励器激励Hopkinson杆,可输出冲击加速度峰值20~30 000 m/s2、脉冲持续时间30~200 μs的冲击加速度。通过设计和编制中小冲击激励驱动控制软件,构建了中小冲击激励控制系统。输入压电叠堆激励器的激励信号是由3个周期一定的正弦信号通过 Hanning窗(升余弦窗)函数整形后获得。
由于压电叠堆激励器的激励能力有限,5 000 m/s2以上需通过测算和设置Hopkinson杆应力波的反射时间,采用应力波波形叠加方式(如10个)提高Hopkinson杆末端输出的加速度,使之加速度输出峰值达到30 000 m/s2以上。见图4。
2.2 激光测量系统
采用自主研制的外差马赫-泽德激光干涉仪与ISO 16063-13推荐的数据处理方法相结合的技术方案[1,3]。
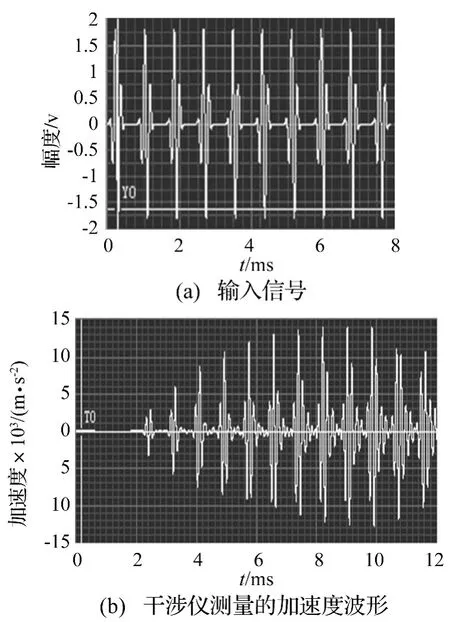
图4 波形叠加激励Fig.4 Excited by superposition of waves
2.2.1 外差马赫-泽德激光干涉仪
多普勒干涉法是将安装有被测传感器的Hopkinson杆端面作为激光多普勒测量系统的运动反射体,该表面受到冲击作用发生位移时,激光信号发生多普勒频移。通过测量激光的频率变化,即可确定位移随时间的变化量。
由于冲击测量时间短,一般都在ms以下量级,因此,外差激光干涉仪的设计思路主要从测量的短时稳定性和准确性考虑。设计采用频率稳定度达10-9的单模稳频He-Ne激光器为激光光源,在测量处于静态平衡位置时,应使光电输出信号具有较高的信噪比,以确保微小的冲击速度变化能引起足够的多普勒频移从而减小激光频率的不稳定对微小运动所引起的频移方向判断不准的影响。同时由于冲击过程中有可能产生横向抖动,将测量光经漫反射以减少横向干扰,此时经漫反射返回到光电接电器的光强最小为5 μW左右。在精心设计光路系统的同时,选用滨松公司生产的高速宽带APD为光电接收器,再经低噪声放大电路放大/调制,使得干涉光电信号动态信噪比达到45 dB以上,确保了冲击校准的稳定性。
研制的高速外差激光干涉仪能够满足1 000 m/s2到1 000 000 m/s2大量程冲击加速度的精确测量,解决了国内现有大g值冲击加速度测量用激光干涉仪完全依赖进口的问题。
2.2.2 数据采集处理
基于虚拟仪器技术,分别构建了高和中小冲击激光测量系统,高冲击硬件选用PXI接口12位/2通道/200MS/s高速数据采集卡5124和控制卡6251,中冲击硬件选用PXI接口14位/2通道/100MS/s高速数据采集卡5122和控制卡6151,并分别以GPIB接口卡作为测量系统实现数据采集处理及控制的硬件接口,它们与其它仪器设备连接构成虚拟仪器的硬件系统。在计算机环境中,依托功能强大的处理单元和高速的数据总线,利用NI公司的LabView图形化软件平台,构建了可视化软面板,使计算机成为具有数据采集、信号控制及分析显示功能的处理中心。
外差激光干涉绝对法冲击测量系统框图见图5。
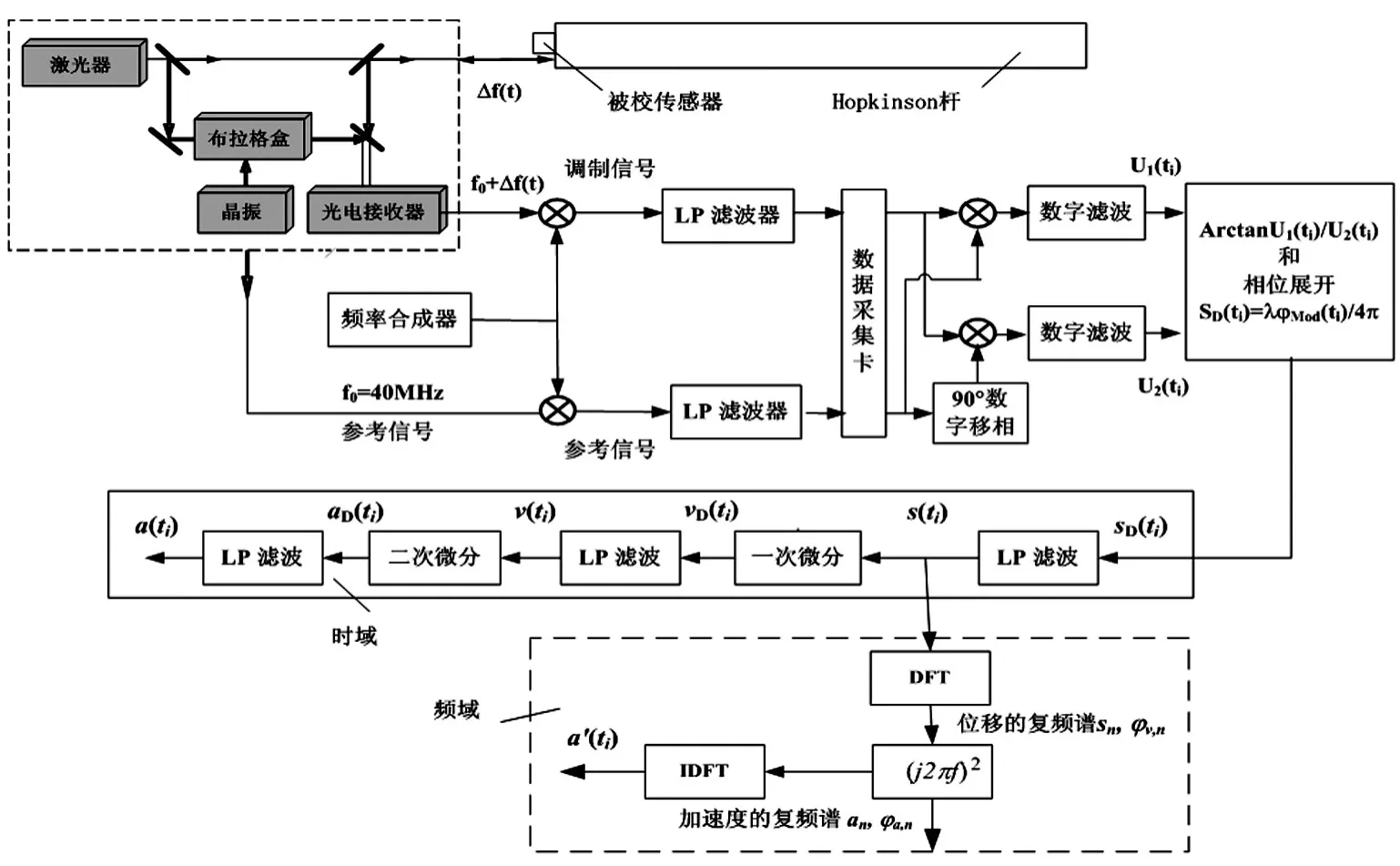
图5 外差激光干涉冲击绝对法测量系统框图Fig.5 Block diagram of shock absolute measurement system by heterodyne laser interferometry
在一个测量周期t0<t<t0+TMeas中,对激光干涉信号与加速度输出信号进行同步采样。在上述测量时间内,采样得到的一路激光干涉信号,通过90°数字移相,从而得到两路正交激光信号分别为{u1(ti)}和{u2(ti)},采样间隔Δt=ti-ti-1。同时,加速度计输出值的采样序列为{u(ti)}。
对于采样得到干涉仪输出值u1(ti)和u2(ti),由下列公式计算调相值序列{φMod(ti)}:
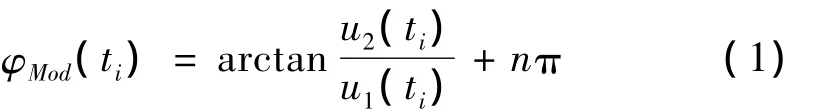
式中:n=0,1,2,…。
通过选择合适的n,可以得到由于反正切运算而卷折的展开相位信息。对得到的展开的连续相位{φMod(ti)},用下式计算得到位移序列。
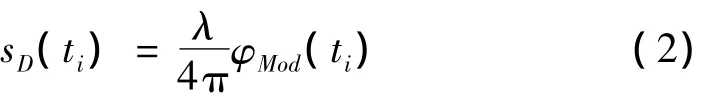
下标D表示受高频噪声影响的序列值。对位移序列{sD(ti)}进行“平滑”滤波,得到位移序列{s(ti)}。从位移信号计算得到对应的加速度信号,采用两种方式,一种是频域微分法,即将得到的{s(ti)}进行DFT计算,得到位移的复频谱。再将位移复频谱乘以(j2πf)2得到加速度的复频谱。用离散傅里叶逆变换IDFT计算加速度序列{a(ti)},并将判断得出的最大值max{a(ti)}作为冲击加速度峰值apeak;另一种方法是时域微分法,即直接对位移信号进行时域数字微分运算从而得到加速度,但此时需要注意选择合适的微分器,否则容易将位移信号中的高频噪声放大。
对同步采样获得的加速度计电压输出信号{u(ti)}进行低通滤波操作,取滤波后得到的序列最大值upeak作为加速度计输出电压波形的最大值。
最后按照式(3)即可计算得到被校加速度计的冲击灵敏度Ssh[1,3]。

2.3.3 数字微分器的设计
由于激光干涉测量得到的是位移信号,为了得到对应的加速度信号,必须对位移信号进行微分运算,但微分运算会放大位移信号中的噪声。为了避免混叠和抑制噪声,采样前,对加速度计和干涉仪输出信号均采用幅频和相频响应较为理想的模拟滤波器滤波,抑制高频信号干扰,以满足装置测量不确定度的要求。同时对于数据处理中的微分运算,为了防止减小运算噪声,采用微分器与数字低通滤波器相结合的方式。微分运算的传递函数形式为H(s)=s,对应的幅度响应曲线为图6中虚线。
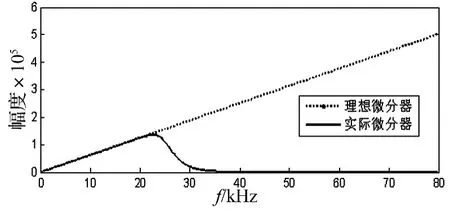
图6 一阶微分器和串联低通滤波器的微分器Fig.6 First-order differentiator(dotted)and differentiator cascaded with low-pass filter(solid)
针对微分器在高频段增益大,对噪声有放大作用的问题,选用微分器与低通滤波器串联的方式。例如需对25 kHz以内的信号进行微分运算,则采用串联FIR低通滤波器的微分器,且设置低通滤波器的截止频率为25 kHz,见图6。在选择的频率范围内与理想的一阶微分器吻合很好;但在高频部分则产生很大的衰减,从而达到了抑制高频噪声的效果。
3 装置主要技术指标
装置的测量范围:冲击加速度峰值20~1 000 000 m/s2、脉冲持续时间 20 ~200 μs。
冲击灵敏度测量的重复性:10 000 m/s2参考条件下优于0.2%;300 000 m/s2参考条件下优于1.0%。
冲击灵敏度测量的不确定度(k=2):1%(50~20 000 m/s2,30 ~200 μs);2%(>20 000 ~100 000 m/s2,50 ~200 μs);5%(>100 000 ~1 000 000 m/s2,20 ~100 μs)。
4 加速度峰值和脉冲持续时间控制特性
采用压电激励器激励方式的中小冲击装置冲击加速度峰值测量下限可达20 m/s2,并且能够通过设定不同的冲击激励信号从而产生特定的冲击加速度波形,精确控制加速度峰值和脉冲持续时间的特性,可实现对冲击波形和其频率分布较为理想的控制,达到抑制高频分量,避免由于加速度计谐振影响造成输出信号失真过大。
在中小冲击激励装置上,对Endevco公司2270压电加速度计和B&K公司2635电荷放大器组成的冲击加速度计套组进行给定加速度500 m/s2下改变脉宽的冲击灵敏度校准,校准结果见图7。
图7显示,激励波形脉宽不一样,得到的冲击加速度灵敏度也不相同。由此可知,冲击校准所得到的冲击灵敏度是一个与激励波形有关的量。描述加速度计冲击激励特性所用的典型冲击灵敏度主要取决于冲击波形和激励的频谱分量,因此不能只用冲击灵敏度去描述一只特定加速度计的特性[7-9]。实验分析可知,冲击灵敏度与激励系统的特性(加速度峰值、冲击脉冲持续时间和冲击脉冲形状)有关,不具有唯一性。冲击灵敏度主要取决于冲击脉冲持续时间,但是如果加速度计与理想的幅值线性发生偏离时,它还取决于加速度的峰值[10-11]。
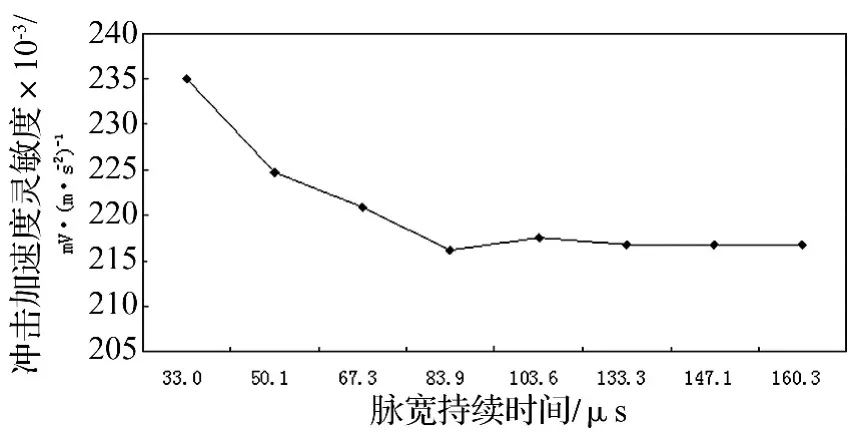
图7 给定加速度500 m/s2下改变脉宽的冲击灵敏度校准曲线Fig.7 The shock sensitivity calibration curve of changed the pulse width in given acceleration(500 m/s2)
5 实验数据
在中小冲击装置上,对2270/2635冲击加速度计套组进行中小冲击灵敏度的校准,校准数据见表1。冲击灵敏度校准的不确定度(k=2):1%(50~20 000 m/s2);2%(其他)[12-13]。
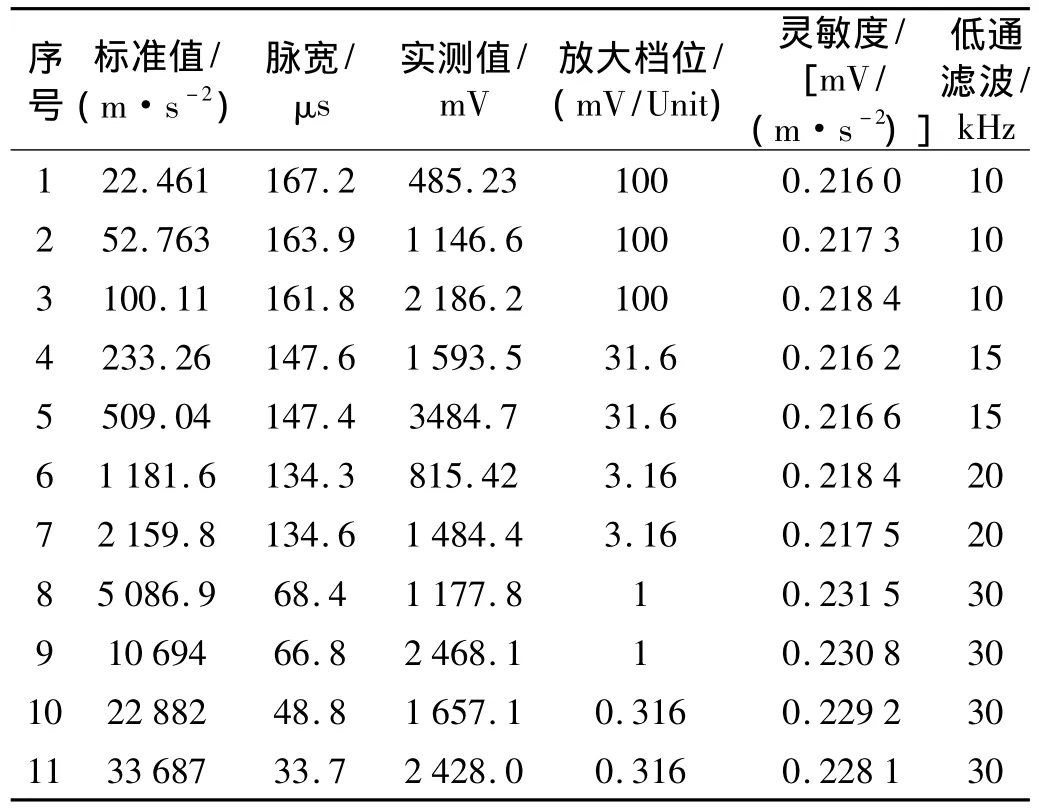
表1 2270/2635校准数据Tab.1 Calibration data of 2270/2635
在高冲击装置上,对B&K公司8309压电加速度计和2635电荷放大器组成的冲击加速度计套组进行高冲击灵敏度的校准,校准数据见表2。冲击灵敏度校准的不确定度(k=2):2%(30 000~100 000 m/s2);5%(其他)[12-13]。
实验结果表明:研究建立的新一代冲击加速度激光绝对法基准装置,采用当前国际最先进的激光干涉冲击绝对校准方法,在冲击加速度峰值20~1 000 000 m/s2和脉冲持续时间20~200 μs范围内,实现了冲击加速度峰值和冲击灵敏度的绝对法测量。拓展了国际标准规定的冲击加速度峰值绝对法测量范围,测量结果的不确定度在可比范围内(200~100 000 m/s2)满足ISO 16063-13:2001“激光干涉法冲击绝对校准”国际标准的要求[1]。
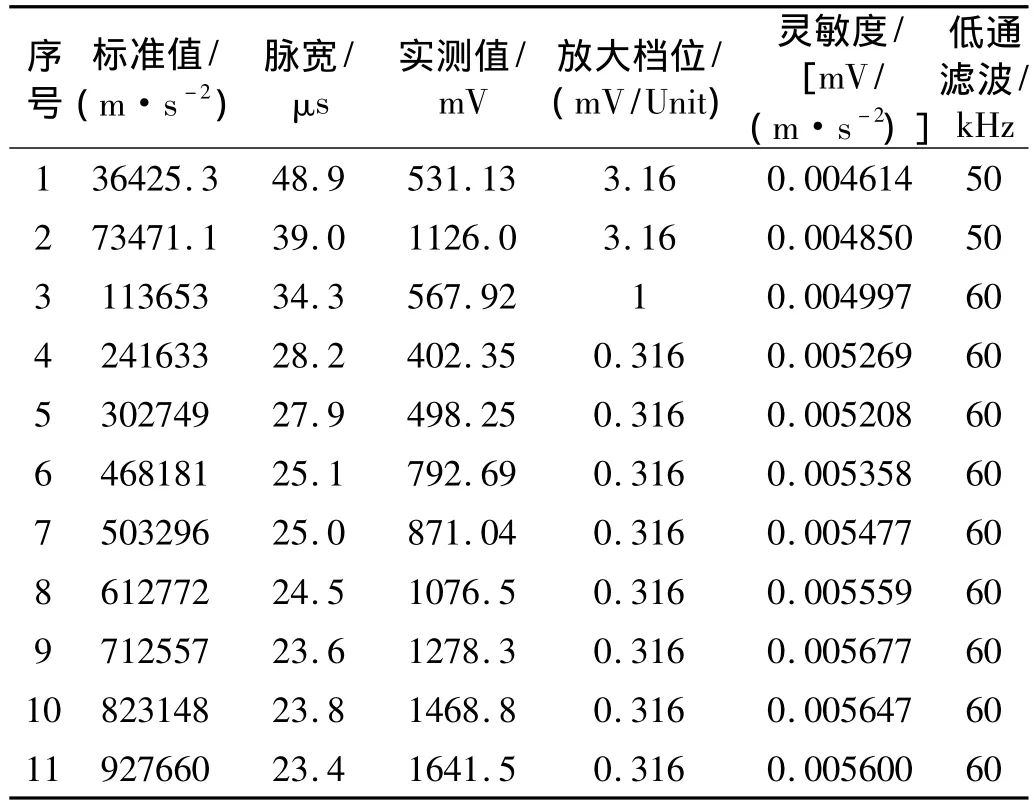
表2 8309/2635校准数据Tab.2 Calibration data of 8309/2635
需要说明的是,本装置采用ISO 16063-13“激光干涉法冲击绝对校准”最新的校准方法,即通过激光干涉法测量冲击过程时间-位移信号实现对直线加速度计的绝对法冲击校准。此方法从根本上有别于速度改变冲击校准方法,其得到的冲击灵敏度也与后者的冲击校准因子不同[1]。
6 结论
新一代冲击加速度国家基准装置的建立实现了与发达国家在冲击校准方法和计量技术上的接轨,可解决我国国民经济各领域对冲击计量提出的宽量程、高准确度的量值溯源需求问题。目前项目科研成果已为我国获得国际互认的6项冲击最高校准能力(CMCs)的确认提供了重要的技术支撑;为亚太区域冲击国际关键比对的方法研究奠定了坚实基础。
[1]ISO 16063-13:Methods for the calibration of vibration and shock transducers-part 13:primary shock calibration by laser interferometry[S].2001.
[2] von Martens H J. Traceability of vibration and shock measurements by laser interferometry [J].Measurement,2000,28:3-20.
[3] Link A,von Martens H J.Calibration of accelerometers by shock excitation and laser interferometry[J].Shock Vib.,2000,7:101-112.
[4] Bruns T,Link A,Elster C.Current Developments in the Field of Shock Calibration[C].Proc.18th IMEKO World Congress(Rio de Janeiro,Brazil),2006.
[5]胡红波,于 梅.Hopkinson杆冲击激励系统的原理与应用[J].计量技术,2011,2:36-38.HU Hong-bo,YU Mei.Principle and application of shock excitation based on Hopkinson bar[J].Measurement Thchnique,2011,2:36-38.
[6] Link A,von Martens H J,Wabinski W.New method for absolute shock calibration of accelerometers. Third International Conference on Vibration Measurements by laser Techniques:Advances and Applications[C].Proc.SPIE,1998,3411:224-235.
[7] Link A, TäubnerA, WabinskiW, etal. Modelling accelerometers for transient signals using calibration measurements upon sinusoidal excitation[J].Measeurement,2007,40:928-935.
[8]ElsterC, Link A, Bruns T. Analysis ofdynamic measurements and determination of time-dependent measurement uncertainty using a second-order model[J].Meas.Sci.Technol.,2007,18:3682-3687.
[9]胡红波,于 梅.基于高冲击激励的加速度计参数识别的研究[J].传感技术学报,2012,25(4):487-490.
HU Hong-bo,YU Mei.Study for parameters identification of an accelerometer based on high shock intensities[J].Chinese Journal of Sensors and Actuators,2012,25(4):487-490.
[10] Link A,von Martens H J.Accelerometer identification using shock excitation[J].Measeurement,2004,35:191-199.
[11] Link A,Täubner A,Wabinski W,et al.Calibration of accelerometers:determination of amplitude and phase response upon shock excitation[J].Meas.Sci.Technol.,2006,17:1888-1894.
[12] Ueda K,Umeda A,Imai H.Uncertainty evaluation of a primary shock calibration method for accelerometers[J].Metrologia,2000,37:187-197.
[13] von Martens H J.Evaluation of uncertainty in measurementsproblems and tools[J].Optics and Lasers in Engineering,2002,38:185-206.

