几何画板在高职数学教学中的应用研究实例
◆张晓良
作者:张晓良,北京电子科技职业学院基础部数学教师,研究方向为几何画板与数学教学(100176)。
几何画板软件是由美国Key Curriculum Press公司制作并出版的一款优秀的数学教学及学习软件。它的全名是“几何画板——21世纪的动态几何”。
自从1996年传入中国以来,几何画板深受广大数学教师的欢迎与喜爱。应用几何画板软件可以很好地解决数学教学中数形结合的问题。由于当时条件的限制,几何画板没有在职业院校得到普及。随着社会的发展和进步,如今多媒体技术非常普及,在职业院校的每个教室里都配备了电脑及投影设备,使得几何画板在数学教学中有了用武之地。
几何画板是一款集绘制几何图形、编辑图形的动画轨迹于一身的软件,其使用之方便、功能之强大超出使用者的想象。很多人因为它占用电脑空间很小,就称其为小软件,甚至轻视了它的功能。当真正了解几何画板之后,一定会为其强大的功能而惊叹的。
笔者是在2000年开始学习、研究几何画板及其使用技巧的,经过10多年的学习与使用,积累了不少的经验。下面就向大家介绍一下在教学中使用过的几何画板课件“正弦型函数”。
正弦型函数是职业院校5年制数学教学的必修内容,这部分内容是学习电工电子技术的基础。讲解这部分内容时,重点是要讲解清楚正弦型函数与正弦函数图象的关系,以及其中的参数A、ω、φ的作用。过去讲这部分内容时,教师要在课前准备好多张绘制好的正弦型函数与正弦函数比较的图象,在课上展示给学生看。这样教学虽然也能帮助学生理解,但是不足之处是展示这些图象时很麻烦、不便修改,而且无法看到由正弦函数变化到正弦型函数的过程。如今,利用几何画板制作的课件就很好地解决了这个问题。
首先,讲解正弦型函数中A的作用。如图1所示,图1(1)显示的是正弦型函数在A=1,ω=1,φ=0时的情形,此时的正弦型函数的图象与正弦函数的图象是重合的。
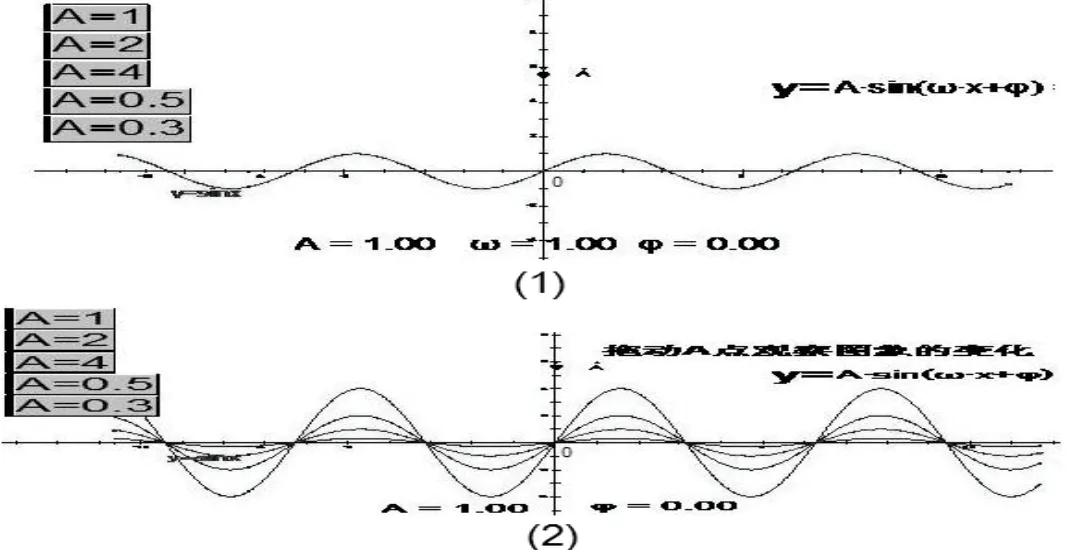
图1
然后,用鼠标单击按钮A=1至A=0.3,可以实现A取值1、2、4、0.5、0.3时正弦型函数的图象;也可以用鼠标拖动图中的A点自由地选择A的取值。这样就把正弦型函数图象随着A的变化而变化的过程动态地表现出来。通过图1的演示,学生已经可以归纳出正弦型函数中A的作用了。
其次,讲解ω在函数中起的作用。如图2所示,图中虚线为正弦函数,实线为正弦型函数。在研究ω的作用时,先令A=1,ω=1,φ=0。在保持A=1,φ=0不变的情况下,通过ω取不同的数值,如ω=0.5,ω=1,ω=2,ω=3,观察并比较它们的周期,学生很快就可以得出结论:正弦型函数在ω增大时,函数周期变小了;反之,ω减小时,函数的周期变大了。经过教师的引导,学生又可以得出正弦型函数的周期与正弦函数的周期2π的关系。此时给予学生印象最为深刻的是:正弦型函数的图象随着ω增大或减小,是横向的压缩或拉长的变化过程。这个演示过程只需要几分钟的时间,难点就被轻松地跨越。
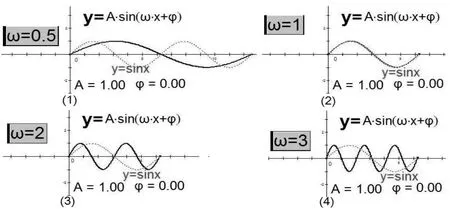
图2

图3
最后,讲解φ在函数中起的作用。在研究φ的作用时,还是先令A=1,ω=1,φ=0。此时正弦型函数与正弦函数图象是重合的。在保持A=1不变的情况下,先演示ω=1时,正弦型函数随着φ的变化而变化的情况;再演示ω=2的情况。如图3所示,图中虚线为正弦函数,实线为正弦型函数。
教师演示时,可以拖动图象中的φ点,使φ的数值由正变负,再由负变正。学生很快就发现“φ由0开始增大时,图象向左边移动;φ由0开始减小时,函数图象向右边移动”的规律。如果只观看图3(1),得出的结论是函数图象左右移动的距离就是|φ|;而观察了图3(2)后,学生才会发现,函数图象向左右移动,不但与φ有关,而且移动的距离还与ω的大小有关。教师可以再演示一下ω=3的情形,然后学生就能发现其中的规律了。
实践中我利用这个课件上课,学生很快就理解并掌握了正弦形函数,并且对其中的参数A、ω、φ的作用印象深刻。因为这些规律都是他们自己“发现”的。
利用几何画板制作的课件,能够帮助学生理解跟多高职数学中的问题。如函数、解析几何、三角、向量、微积分中的很多问题。我也制作了很多课件,希望能与大家交流。
[1]刘胜利.几何画板与微型课件制作[M].北京:科学出版社,2001.
[2]潘天士.中学数学课件制作与技巧[M].北京:机械工业出版社,2004.

