轿车车内低频噪声的判定参数探讨*

高书娜，邓兆祥

(1.西南大学工程技术学院，重庆 400716;2.重庆大学，机械传动国家重点实验室，重庆 400030)

前言

如何快速预测控制200Hz以内的轿车车内低频噪声，是当前车内噪声研究的一项重要内容。基于结构声腔耦合系统的频率响应分析，进行车内声压响应预测和控制，是目前被广泛采用的一种车内低频噪声计算分析方法，但其计算过程的实现较为复杂，尤其当原设计车身需要进行结构改进时，还须增加板件声压贡献分析、声压灵敏度分析或车内噪声优化分析等［1-3］，此时不仅增加了分析计算的内容，还延长了车身结构改进设计周期。

文献［4］中以某简单耦合系统为研究对象，通过分析得出声压响应幅度的判定参数，并将其应用于车身的低噪声设计。实际车身结构较为复杂，往往要通过有限元法来计算结构和声腔的模态。为此，本文在该研究的基础上，采用有限元法计算声压响应幅度判定参数，并与解析式法进行对比，分析有限元法的计算精度;然后以某轿车为例，分析其车身结构声腔耦合系统的声压响应幅度判定参数。

1 声压响应幅度判定参数的有限元法计算与精度分析

极坐标下一般腔体结构的内部声压表达式［5-6］可写为

式中符号请参见原文献。

式(1)中求和符号之前的幅值系数是空气密度、声速平方、结构和声腔的接触面积和激励力四者的乘积。当耦合系统和激励力确定后则为定值，而求和符号内的Cnp、Fnp、Ψs和Ψa成了决定声腔响应的4个关键参数。因此，以下采用有限元法对该4个参数进行计算。

1.1 4个参数的有限元法与解析式计算结果对比

以含有一个弹性面的刚性长方体结构和声腔的耦合系统为研究对象(模型参数，详见文献［4］)，利用成熟商业软件分别计算结构和声腔的模态，任选某1阶结构和声腔的振型绘于图1，结构的前10阶模态频率见表1，声腔的前10阶模态频率见表2。

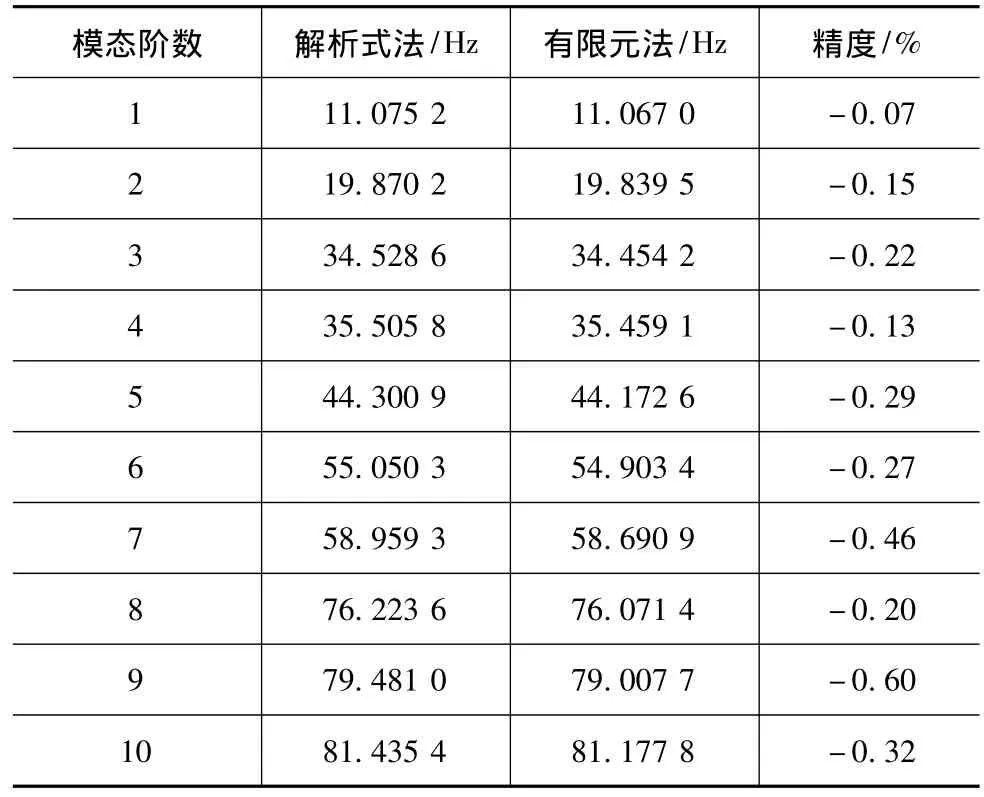
表1 结构模态频率的解析式和有限元结果对比

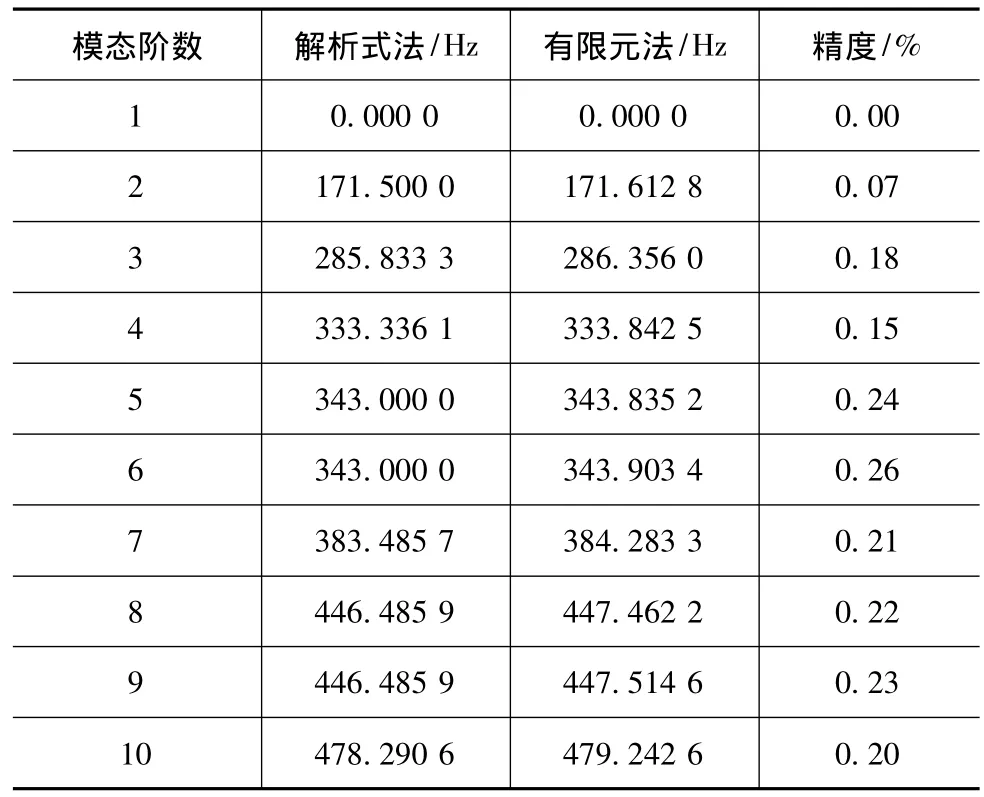
表2 声腔模态频率的解析式和有限元结果对比

1.1.1 振型耦合系数分析

分别利用解析式和有限元法计算出简单耦合系统的振型耦合系数，两种计算结果非常接近［7］。表明利用解析式和有限元法计算出的振型耦合系数吻合很好。

1.1.2 频率重叠系数分析

表1和表2中，解析式法和有限元法计算出的模态频率差别均在1%以内，表明有限元法计算结果的精度较高。激励频率50Hz时，频率重叠系数的解析式计算结果见表3，将表1和表2中的值带入式(3)后的有限元计算结果见表4。

对比表3和表4中的数据，发现他们最大相差0.05，其余则几乎相等，说明利用解析式和有限元法计算出的频率重叠系数吻合很好。

1.1.3 结构振型在激励点处的分量

根据结构模态振型的解析式和有限元计算结果，结合式(4)和式(5)，计算结构振型在激励点处的分量，结果列于表5。

表3 Fnp的解析式结果(扩大到105倍)

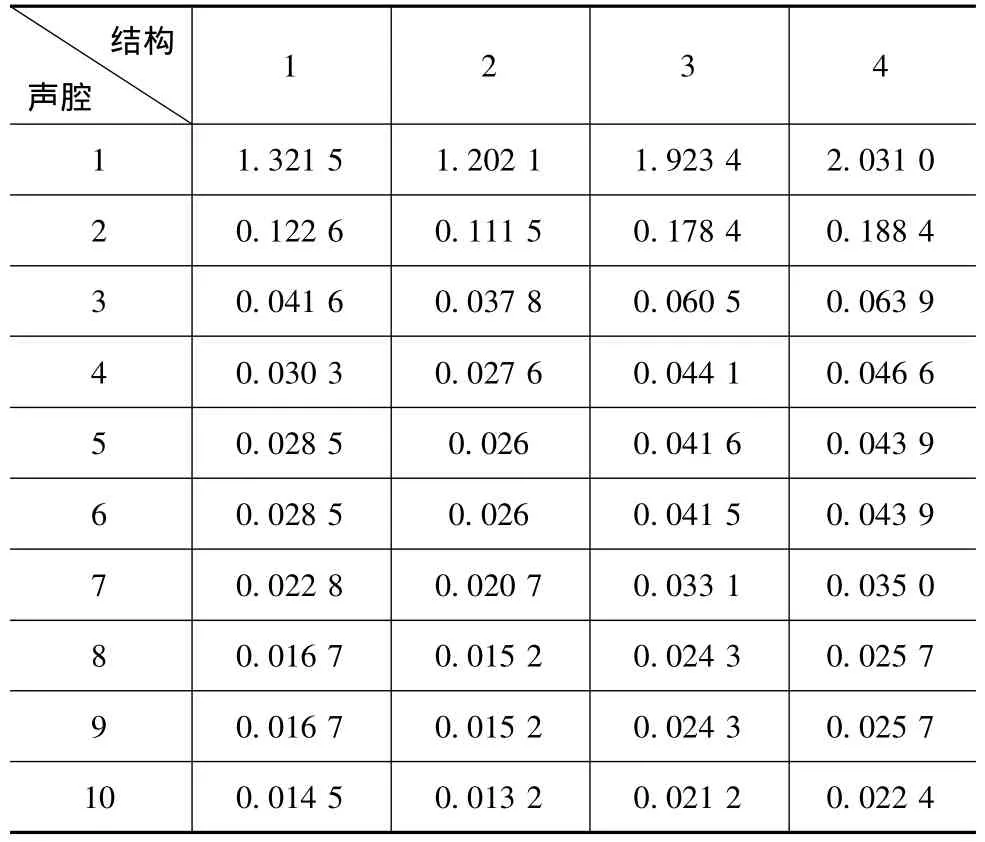
表4 Fnp的有限元结果(扩大到105倍)

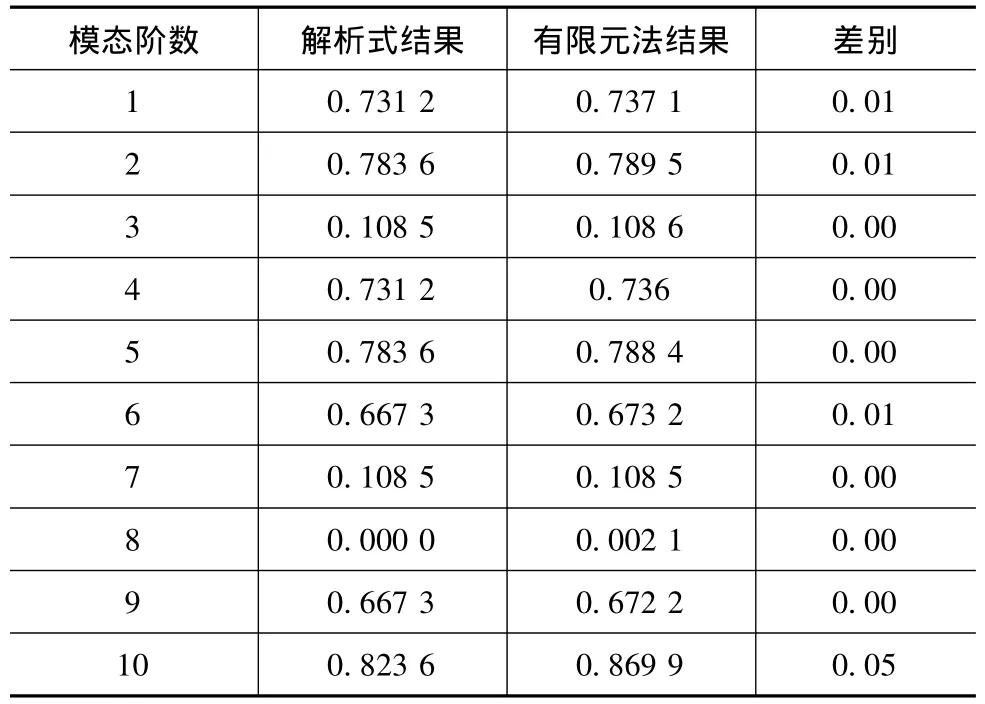
表5 Ψs的解析式与有限元结果对比

由表5可见，两种计算结果最大相差0.05，其余则几乎相等，说明利用解析式和有限元法计算出的结构振型在激励点处的分量吻合很好。

1.1.4 声腔振型在响应点处的分量

根据声腔模态振型的解析式和有限元计算结果，结合式(6)和式(7)，计算声腔振型在响应点处的分量，结果列于表6。

表6 Ψa的解析式与有限元结果对比

由表6可见，两种计算结果非常接近，说明利用解析式和有限元法计算出的声腔振型在响应点处的分量吻合很好。

综上所述，结合有限元法计算出的Cnp、Fnp、Ψs、Ψa等4个参数值，与解析式计算结果的吻合程度较高，表明有限元法计算出的4个参数的精度较高，可用于后续讨论。

1.2 腔内声压响应的计算结果对比

利用上节中计算得出的4个参数，带入式(1)计算出腔内声压响应，与直接利用解析式计算出的腔内声压响应作对比分析，进一步验证4个关键参数的有限元法计算精度。

腔内声压响应的两种计算结果绘于图2中，可见两种计算结果吻合很好。

1.3 判定参数的有限元法计算

由上述 4 个关键参数得到 Cnp、Fnp、CnpFnp、CnpFnpΨs、CnpFnpΨa和 CnpFnpΨsΨa6 种组合。通过在结构和声腔主导的两种声压响应峰值频率下计算以上6组参数值，并分析前5组参数值和第6组参数值的一致性程度，找到最优相似矩阵，最终确定了声压响应幅度的判定参数为 CnpFnpΨs［4］。

将上节中计算得出的 Cnp、Fnp、Ψs等3个参数的数值带入式(1)，而省略参数Ψa，计算出腔内声压响应(即利用声压响应幅度判定参数，计算腔内声压响应)，与直接利用解析式计算出的腔内声压响应进行对比，结果如图3所示。

由图3可见，两条曲线仍然吻合较好，说明:(1)利用判定参数CnpFnpΨs计算腔内声压响应时精度较高;(2)判定参数CnpFnpΨs的有限元法计算精度也较高。

上述研究结果表明:声压响应幅度判定参数的有限元法计算精度较高。当耦合系统的结构和声腔模态难以采用解析式计算时，其声压响应幅度判定参数可采用有限元法进行计算。

2 某轿车车身结构声腔耦合系统的声压响应幅度判定参数分析

为研究根据简单耦合系统确定的声压响应幅度判定参数在汽车车身结构声腔耦合系统中的适用性，以某轿车为例，重点对比几个典型情况下，车内声压响应的频率响应和声压响应幅度判定参数计算结果，以确定用判定参数来预测车内声压响应的精度。

建立的某型轿车车身结构声腔耦合系统模型见图4，该耦合系统的车身结构和车内声腔模型均经过试验验证。

几阶典型的车身结构模态和车内声腔模态的试验结果与有限元计算结果的对比列于表7中。由表7可见，它们的频率相对误差均在3%以内，精度较高，可满足分析精度要求。

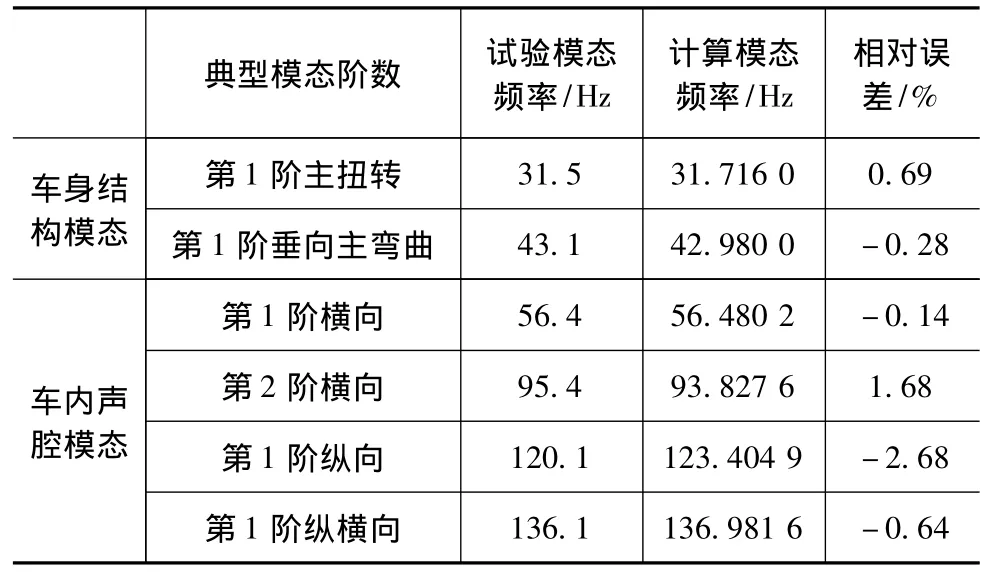
表7 试验模态和计算模态对比

已知对车身刚度影响较大的是骨架梁结构，从图4的车身结构中分离出的骨架梁结构见图5，首先计算单个骨架梁在两端施加固定约束时的第1阶弯曲模态频率，然后调整骨架梁结构参数，使其第1阶约束弯曲模态频率呈一定倍数变化，计算各对应情况下的车内声压响应，分析找出灵敏度较大的骨架梁列于表8中。当它们分别取表8中的参数值时，耦合系统50Hz下的频率响应计算结果见图6;声压响应幅度判定参数矩阵CnpFnpΨs中，各个元素求和计算结果见图7。

若要降低车内声压响应，可通过降低声压响应幅度判定参数CnpFnpΨs来实现，从减小结构声腔振型耦合系数Cnp、频率重叠系数Fnp、结构振型在激励点处的分量Ψs等3个方面进行。又知，一般结构改进时不希望对已经成型产品做较大变动，而Fnp和Ψs一般不会有较大变化，因此振型耦合系数Cnp成为降噪的主要途径。要降低振型耦合系数Cnp，根据定义可通过调整关键结构和声腔模态(关键的结构和声腔模态可从声压响应幅度判定参数的柱状图中直观看出)在耦合面上的振型分量［5，8］来实现，从而确定车身结构需要调整的区域和结构需要加强还是减弱。

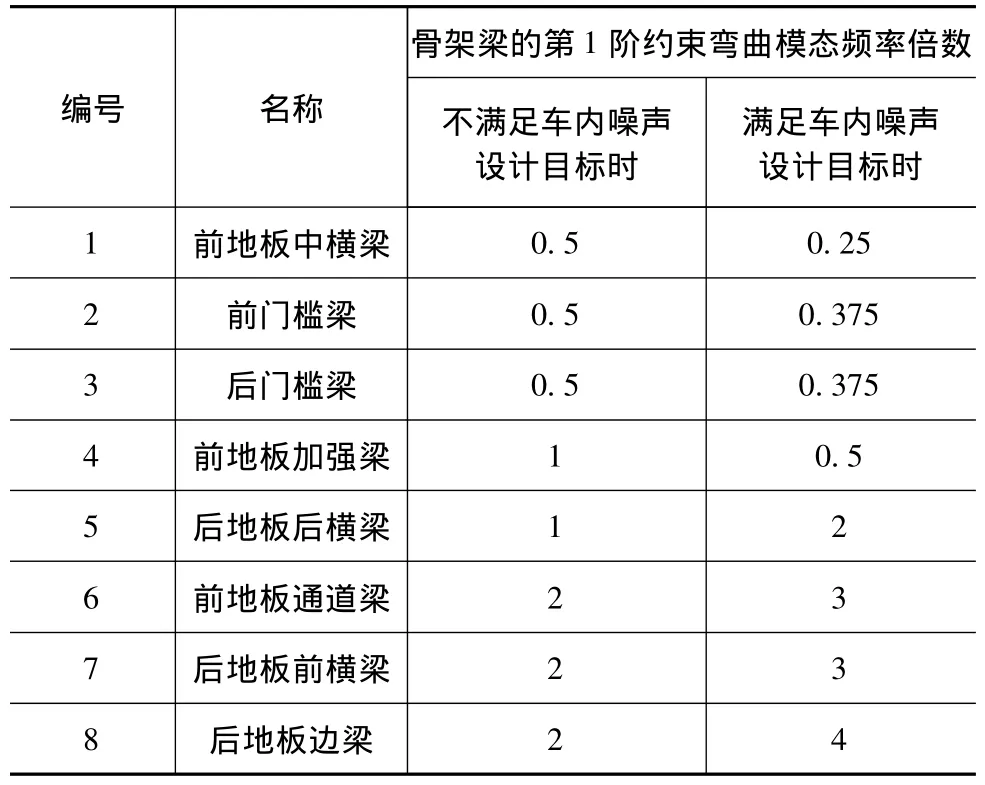
表8 骨架梁参数表

另外，由图7可知，满足车内噪声设计目标时，骨架梁诸零件算得的判定参数值最大约为1.186 5×10-4。因此可以得出结论:在车身结构设计阶段，若能使车身结构声腔耦合系统的判定参数值≤1.19×10-4，即可满足设计目标。但这只是根据本文研究的车型得出的判定参数限值，其它车型情况如何，尚须增加分析车型的数量，才能得出更为普遍的结论。

3 结论

基于空腔内声压响应计算式，探讨轿车车身低频噪声的声压响应幅度判定参数，主要有以下结论。

(1)不论是声压响应4个关键参数Cnp、Fnp、Ψs、Ψa还是声压响应幅度判定参数 CnpFnpΨs，用有限元法计算的精度都较高;与解析式的计算结果相当吻合。说明当耦合系统的结构和声腔模态难以采用解析式计算时，可以采用有限元法进行腔内声压响应的计算。

(2)某型轿车典型情况下的参数CnpFnpΨs计算结果和耦合系统频率响应计算结果趋势有较好的一致性，说明参数CnpFnpΨs也是轿车车身结构声腔耦合系统的声压响应幅度判定参数。

(3)利用参数矩阵CnpFnpΨs，可以明确分析频率下形成声压响应的主要结构和声腔模态，并为降低较大的声压响应提供结构和声腔模态在耦合面上振型分量的调整方向，从而快速定位车身结构改进位置和改进方向，为设计阶段的轿车车内低频噪声优化设计提供新思路。

［1］ 高书娜，邓兆祥，胡玉梅.基于声压灵敏度分析的轿车车内低频噪声优化［J］.吉林大学学报，2009，39(5):1130-1136.

［2］ Han X，Guo Y J，Yu H D，et al.Interior Sound Field Refinement of a Passenger Car Using Modified Panel Acoustic Contribution A-nalysis［J］.International Journal of Automotive Technology，2009，10(1):79-85.

［3］ 张军，兆文忠，谢素明，等.结构-声场耦合系统声压响应优化设计研究［J］.振动工程学报，2005，18(4):519-523.

［4］ 高书娜，邓兆祥.车身低噪声设计新方法［J］.机械工程学报，2012，48(12):96-102.

［5］ Fahy Frank.Sound and Structural Vibration，Radiation，Transmission and Response［M］.London:Academic Press，1985.

［6］ Krylov V V.Simplified Analytical Models for Prediction of Vehicle Interior Noise［C］.Proceedings of ISMA2002，International Conference on Noise and Vibration Engineering，Leuven，BELGIUM:1973-1980.

［7］ Gao Shuna，Deng Zhaoxiang.The Mode Shape Coupling Mechanism of the Structural-acoustic Coupled System［J］.Chinese Journal of Automotive Engineering，2011，1(4):348-354.

［8］ 高书娜.轿车车身低频结构声耦合机理及降噪设计研究［D］.重庆:重庆大学，2011.