无转矩传感器汽车电动助力转向系统的控制策略*
熊 亮,刘和平,彭东林
(1.重庆大学,输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)
前言
汽车电动助力转向(electric power steering,EPS)系统在燃油效率、模块化、路感可调性和环境友好性等各方面具有比传统转向系统明显的优势。根据助力电机在齿轮和转向柱总成上位置的不同,EPS系统有转向柱助力式、齿条助力式、小齿轮助力式和双小齿轮助力式4种类型[1]。小齿轮和转向柱助力式应用于轻型车辆,而双小齿轮助力式应用于重型车辆[2]。它们在构成上都具有3个基本部件:电控单元(electric control unit,ECU)、助力电机和安装在转向柱上的转矩传感器。
现有各种类型EPS系统的控制策略大都依赖于转矩传感器:ECU通过转矩传感器测得转向过程中的转向柱转矩,采用控制器控制助力电机电流给出相应大小的助力转矩。文献[3]中描述了转向柱式EPS系统的建模和采用转矩传感器输出的控制系统的性能。文献[4]中试图改进驾驶员路感并采用H∞控制方法以确保足够的助力。文献[5]中探讨了EPS系统开发中的控制和路感问题。文献[6]中重点分析了EPS控制系统的稳定性,减小高助力水平下转向柱的振动,以及在静止或低速条件下的路感和控制性能。文献[7]中分析和设计了一种双小齿轮EPS系统的最优控制系统,它采用状态反馈而取消转矩传感器,但最优控制方法计算过于复杂,难以工程应用[8]。
采用转矩传感器虽然使系统的控制策略容易实现,但它不仅增加了系统成本,其安装匹配也增加了系统机械部分的复杂性,特别是转矩传感器中的扭杆降低了转向柱的刚度,影响了驾驶员路感和控制的稳定性。取消现有EPS系统中的转矩传感器,尤其是去掉扭杆等机件可以使转向柱由输入轴-扭杆-输出轴结构简化为单一转向轴结构,将大大降低系统的复杂性和成本,提高系统的可靠性。不同类型的EPS系统的基本原理相同。本文中以转向柱助力式EPS系统为研究对象,采用仿真和台架实验的方法分析其无转矩传感器控制下的特性。
首先采用拉格朗日方程建立系统的动力学运动方程,再结合电机动态电压平衡方程建立无转矩传感器转向柱助力式EPS系统的动力学状态空间模型;接着在分析系统可控可观测性的基础上,提出了一种采用观测器技术的无转矩传感器EPS控制系统;然后设计了转向柱转矩卡尔曼观测器和台架实验系统;最后采用PID控制器建立了无转矩传感器EPS系统的闭环控制系统。
1 系统动力学模型
转向柱助力式EPS系统的动力学耗散模型由系统中所有的质量、转动惯量以及它们与各弹簧和阻尼元件相互作用而构成。考虑到系统主要为低频运动,简化模型中忽略了高刚度元件的影响。
图1为无转矩传感器转向柱助力式EPS系统的简化模型。图中齿条通过小齿轮与转向柱连接,连接有独立转动轴的助力电机通过减速齿轮与转向柱连接。轮胎连接杆连接齿条和轮胎。模型中忽略了轮胎连接杆和轮胎的质量,以及轮胎运动、摩擦和齿轮等传动部件的惯性。
转向柱助力式EPS系统的运动方程可由拉格朗日方程得到。其一般形式为
式中:qi为系统相应的运动坐标,Qi为qi方向的广义外力,n为自由度。
对转向柱、电机轴和齿条的运动,分别采用拉格朗日方程,可得动力学运动方程为
式中:Jc为转向盘和转向柱的转动惯量;θc为转向柱角度位置;Bc为转向柱扭转阻尼系数;Kc为转向柱扭转刚度系数;p为齿条位移;rp为小齿轮半径;Td为转向盘转矩;Jm为电机轴和转动箱的转动惯量;θm为电机轴角度位置;Bm为电机轴扭转阻尼系数;Km为电机轴扭转刚度系数;N为电机减速比;Ka为电机的转矩常数;i为直流助力电机绕组电流;Mr为齿条等效质量;Br为齿条等效阻尼系数;Kr为齿条等效刚度系数。
此外,直流助力电机的电压平衡方程为
式中:L为定子绕组电感量;R为绕组电阻;υ为电机端电压;Kb为电机绕组反电动势系数。
式(2)~式(5)为转向柱助力式EPS系统的机电方程。EPS为开环系统,有转向盘转矩Td与助力电机端电压υ两个输入和转向柱转矩Tc一个输出。
2 设计方法
2.1 无转矩传感器控制策略
以上线性EPS系统的状态空间描述为
式中:n(t)为随机测量噪声。EPS模型的状态为
转向盘输入转矩和电机端电压作为系统输入:
以转向柱转矩Tc=Kc(θc-p/rp)作为系统输出。系统矩阵A,输入矩阵B,输出矩阵C,分别为
验证系统的可控、可观测性:Td和υ两个控制输入均使用时,系统可控;Td单独输入时,系统可控;υ单独输入时,系统可控;使用Tc测量,系统可观测;使用θm测量,系统可观测。从以上分析也可看出,采用θm测量输出、Td和υ两个控制输入同样可以构成EPS控制系统。相比Tc的测量,θm的测量具有简单和低成本的优势。
采用观测器技术,可以建立如图2所示的EPS控制系统[9-10]。观测器由电机端电压υ和系统输出θm观测出系统状态,得到转向柱转矩观测量Tc-obv。PID电流控制器根据Tc-obv和车速vspeed的大小控制助力电机电流给出相应的助力大小。
2.2 观测器设计
采用卡尔曼滤波器作为观测器是一种在线线性最小方差优化递推算法,递推式计算可由数字信号处理器在线完成,在随机干扰和噪声下也能准确观测出系统状态[11]。卡尔曼观测器的状态方程为
式中Kkf为增益矩阵。对EPS系统中的来自传感器的测量噪声和路面干扰可设为随机高斯白噪声干扰,并采用其噪声协方差用于卡尔曼观测器设计。对式(8)中系统输入u的分量Td,采用将卡尔曼观测器输出Tc-obv作为其下一次递推计算的Td的估计。此代替引起的误差可作为系统的状态噪声来处理,在递推计算中由卡尔曼观测器予以校正。转向柱转矩观测器如图3所示。
卡尔曼观测器状态估计的关键是确定增益矩阵Kkf,它与协方差矩阵P,系统噪声矩阵Q和测量噪声矩阵R的初值有关。P的初值一般可设为0。通常情况下,Q和R是未知的。假定系统噪声和测量噪声不相关,系统噪声矩阵Q和测量噪声矩阵R都是对角阵,其对角元素可根据这些噪声的随机特性通过实验来确定。Q和R的改变会影响到闭环系统的动态和稳态性能。
式中:a为可调参数,用于调整闭环系统的性能;a1、a2…a7分别为转向柱角度、转向柱转速、电机轴角度、电机轴转速、齿条位移、齿条线速度和电机电流等的权重系数。
式中:I为单位矩阵;b为系数。
2.3 台架实验系统设计
为验证无转矩传感器EPS控制系统的有效性和性能,设计了转向柱助力式EPS台架实验系统,如图4所示。齿条两侧装有弹簧以模拟汽车前轮的转向阻力。采用高精度磁编码器AS5145测量直流助力电机转子位置。转矩传感器用于测量转向盘转向过程中的转向柱转矩。基于浮点DSP的TMS320F28335电路系统采集助力电机转子位置、端电压和电流等信息,递推计算卡尔曼观测器并执行PID控制算法。为便于比较分析,将采集的转向柱转矩量和观测量同时通过D/A转换器输出。
3 实验与结果分析
在工作频率范围内,EPS系统应能无振荡地提供充足的助力,使其保持更好的稳定性和抵抗外部干扰的能力。熟练的驾驶员操纵转向盘的频率能达到3~5Hz[3]。因此,在此频率范围之内应具有比高频更高的助力增益。采用表1所示的EPS系统参数,对图4所示的无转矩传感器EPS控制系统分别在MATLAB中进行了系统仿真实验和EPS台架实验。噪声矩阵Q和R的可调参数选择为:a=106,a1=0,a2=1,a3=a4=…=a7=0,b=10。比较了系统的开环、有转矩传感器和无转矩传感器的闭环性能。
3.1 系统仿真研究
3.1.1 频域特性和鲁棒性
图5为以转向盘转矩Td为输入,转向柱转矩Tc为输出的EPS系统幅频特性。可以看出,开环和闭环系统对低频转向盘转矩Td输入均能提供较高的助力增益;对高频输入也都有较强的抑制能力,但闭环系统在工作频率范围内具有较平坦的响应。无转矩传感器的闭环响应与有转矩传感器的闭环响应比较接近。
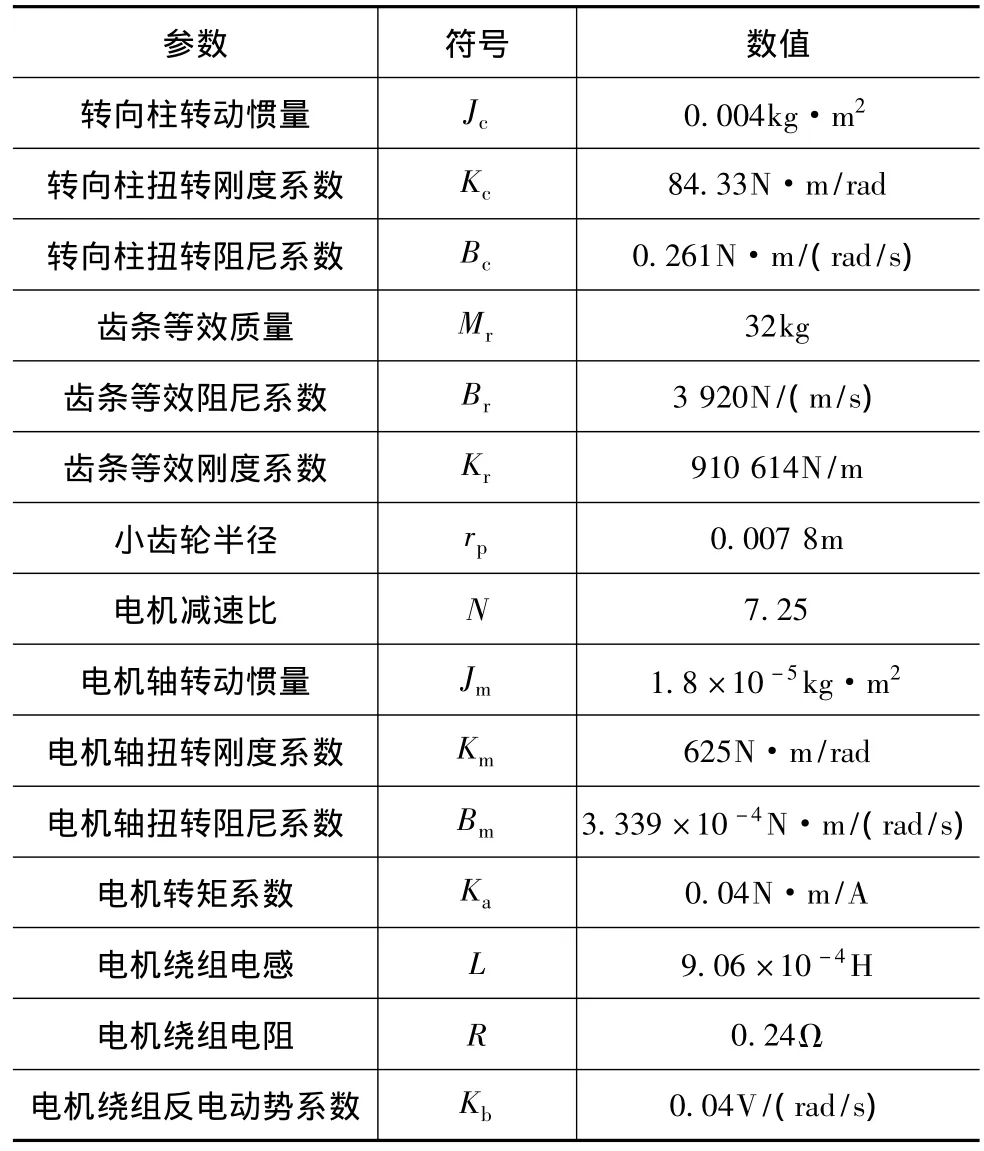
表1 EPS系统参数表
3.1.2 时域特性
转向盘转矩Td阶跃输入下,开环和闭环系统转向柱转矩Tc的响应如图6所示。闭环系统在工作频率范围变小的情况下,其阶跃响应的调节时间比开环系统长约0.1s。
此外,在保持噪声矩阵Q和R中参数不变的情况下,改变参数a的值,可以改变无转矩传感器EPS系统的闭环调节时间,如图7所示。随a值增大,阶跃响应的调节时间缩短,但系统超调量相应增大。系统设计中可通过实验的方法调整a值,以得到较好的系统性能。
3.2 系统台架实验研究
无转矩传感器台架实验系统执行图2所示的控制算法,通过D/A转换器输出的转向柱转矩Tc实时波形如图8所示。从图中可以看出,系统中转矩传感器的输出和本文中设计的卡尔曼转矩观测器的输出基本一致。
4 结论
EPS系统的仿真和台架实验表明,对EPS系统采用无转矩传感器控制策略能基本达到有转矩传感器EPS系统的特性。本文中设计的转矩观测器是有效的。采用转矩观测器技术不仅可以取消现有EPS系统中的转矩传感器、降低系统的机械复杂性和成本,还能得到EPS系统中的助力电机和转向柱的各种状态信息,提高了系统的性能。
[1] Gordon J.Power Steering Turns a Corner[J].Motor Age,2000,119(8):16-22.
[2] Kozaki Y,Hirose G,Sekiya S,et al.Electric Power Steering(EPS)[J].Motion and Control,1999(6):9-15.
[3] Aly Badawym,Jeff Zuraski,Farhad Bolourchi,et al.Modeling and Analysis of an Electric Power Steering System[C].SAE Paper 1999-01-0399.
[4] Sugitani N,Fujuwara Y,Uchida K,et al.Electric Power Steering with H-infinity Control Designed to Obtain Road Information[C].Proc.American Control Conf.,1997:2935-2939.
[5] Zaremba A,Liubakka M K,Stuntz R.Control and Steering Feel Issues in the Design of an Electric Power Steering System[C].Proc.American Control Conf.,1998,1:36-40.
[6] Zaremba A,Davis R.Dynamic Analysis and Stability of a Power Assist Steering System[C].Proc.American Control Conf.,1995:4253-4257.
[7] Manu Parmar,Hung John Y.A Sensorless Optimal Control System for an Automotive Electric Power Assist Steering System[J].IEEE Transactions on Industrial Electronics,2004,51(2):290-298.
[8] 何仁,李强,郭孔辉.LQG理论的电动助力转向系统最优控制[J].农业机械学报,2007,38(2):17-21.
[9] 刘和平,熊亮,等.一种无转矩传感器的汽车电动助力转向系统:中国,CN101624063A[P].2010-01-13.
[10] 刘和平,熊亮,等.一种无传感器汽车电动助力转向系统的控制方法:中国,CN101691124A[P].2010-04-07.
[11] 王成元,夏加宽,杨俊友,等.电机现代控制技术[M].北京:机械工业出版社,2006:208-216.

