利用EXCEL进行线性拟合的应用

徐含青 / 苏州市计量测试研究所

0 引言

在日常计量工作中，常常要处理较为繁琐的数据。作为一线计量人员，如何不断地提高自己的实践与理论应用，一直是追求的目标。

本文针对日常工作中的数据处理与不确定度评定分析中经常要用到的线性曲线拟合与线性方程推导的多种方法应用进行介绍，从而提高工作效率。

1 基于工具EXCEL2007

表1以一组热电偶扩展不确定评定数据为例说明具体应用（基于工具EXCEL2007）。

表1 一组热电偶扩展不确定评定数据

选中所有数据，“插入-散点图-带平滑线和带数据标记的散点图”，初步提取出拟合曲线，如图1所示。

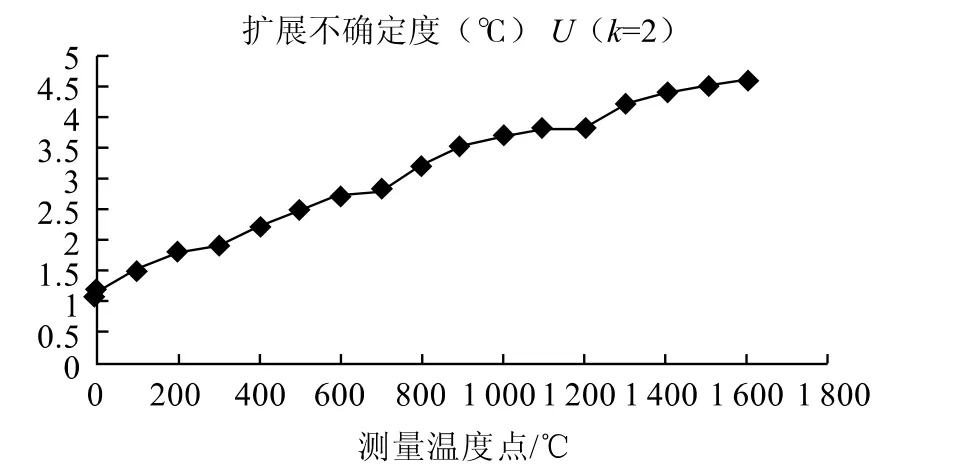
图1 拟合曲线

曲线拟合最基本的原理是基于最小二乘法的应用，如何将上述曲线拟合出线性回归方程y = kx + b，其中x 为自变量，此处为测量温度点。y为因变量，此处为扩展不确定度。k为未知斜率，b为未知截距。根据最小二乘法原理，回归分析式推导出：

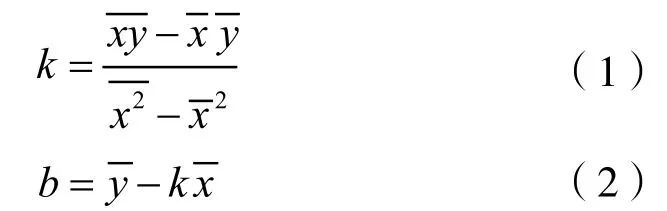
利用表1数据，通过计算得出表2数据。

表2 计算所得数据

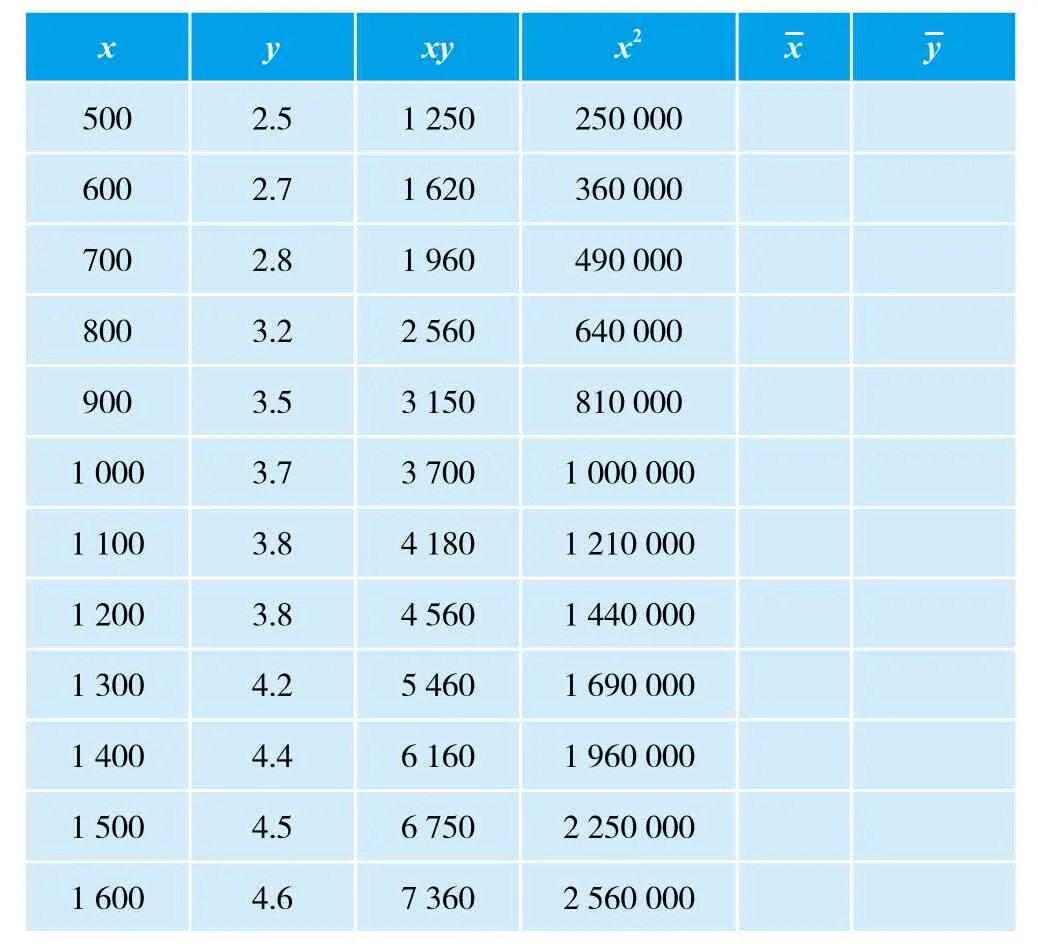
x y xy x2 x y 500 2.5 1 250 250 000 600 2.7 1 620 360 000 700 2.8 1 960 490 000 800 3.2 2 560 640 000 900 3.5 3 150 810 000 1 000 3.7 3 700 1 000 000 1 100 3.8 4 180 1 210 000 1 200 3.8 4 560 1 440 000 1 300 4.2 5 460 1 690 000 1 400 4.4 6 160 1 960 000 1 500 4.5 6 750 2 250 000 1 600 4.6 7 360 2 560 000

继续计算出下列结果：

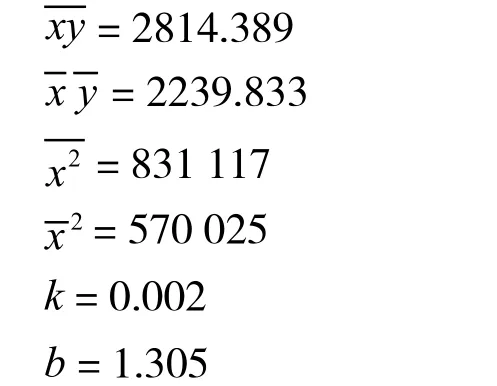
从而得到回归方程：y = 0.002x + 1.305

于是，可以利用公式生成曲线从而完成拟合。

这是从最原始的数据推导出斜率与截距，每次这样应用非常繁琐。现从实际应用出发，寻求更加简单的方法自动生成线性回归方程与曲线。

用EXCEL中现有函数LINEST（）与索引函数index（）取出算得的参数：

从而直接求取得到斜率与截距。

如果每次输入公式较为繁琐或者对函数应用不太熟悉的话，介绍一种最简单的方法，能够更加迅速简单地得到曲线与回归方程。

在EXCEL2007中，选中生成最初的拟合曲线，然后点击“布局-趋势线-其他趋势线”选项，选择曲线类型为“线性”，选择“显示公式”复选框,从而可以一步到位地生成出回归曲线与回归方程，结果如图2所示。可见生成的回归方程与一开始利用最小二乘法算得的斜率与截距一致，从而达到殊途同归的效果。

2 验证趋势线的正确性

下文进一步对直接计算得出的方程生成曲线验证趋势线的正确性。

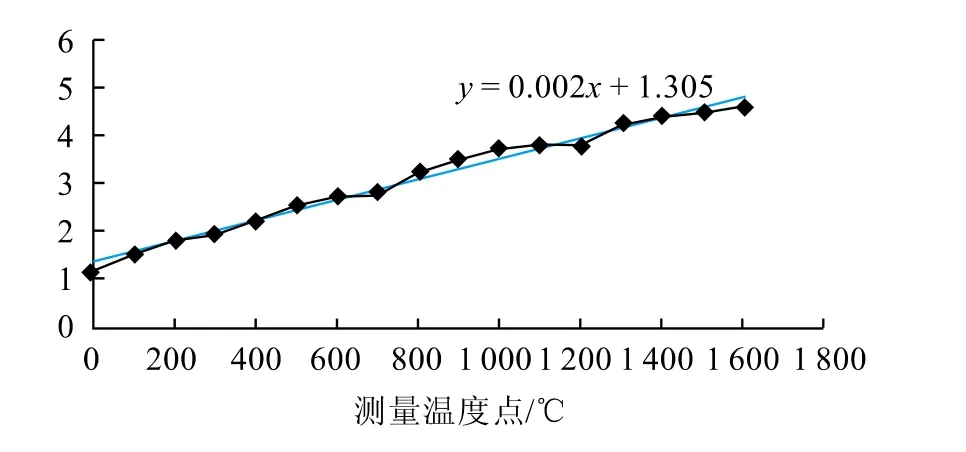
图2 回归曲线与回归方程

利用名称管理器添加两个名称，名称x“引用位置”为”sheet1! A4”,名称y“引用位置”输入宏表函数=”EVLUATE（sheet1！ E 2）”，拖拽后生成C列数据（见表3）。利用表3数据生成散点图与趋势线（见图3）。

表3 生成数据

发现此处两条直线虽然截距与斜率均一致，但生成的直线并不重合，仔细探究原因，是因为数据准确度导致的误差，双击趋势线方程调整数据准确度后发现真正的回归方程为

图3 生成散点图与趋势线

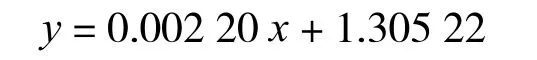
调整函数表达式，重新生成散点图与趋势线，如图4所示。两条直线重合，从而以上方程与曲线得到严格验证。

图4 重新生成散点图与趋势线

3 结语

本文利用原始的最小二乘算法，EXCEL自带的函数应用，EXCEL2007中新增的曲线分析，达到了相同的效果，从底层算法开始推导，通过不断摸索，得到了更为简便的应用方法。

[1]全国温度工作器具计量技术委员会. JJG141-2000 [S]. 北京：中国计量出版社，2000.

[2]全国温度计量技术委员会. JJG351-1996[S]. 北京：中国计量出版社，1996.

[3]全国法制计量技术委员会. JJF1059-1999[S]. 北京：中国计量出版社，1999.

[4]陆健. 最小二乘法及其应用[J]. 中国西部科技, 2007(9)： 19-21.