催化裂化原料特性因子的计算

程 从 礼

（中国石化石油化工科学研究院，北京 100083）

特性因数K常用于划分石油和石油馏分的化学组成，在评价催化裂化原料的质量上被普遍使用。特性因数K值又称Watson K值或UOP K值［1］，是油品平均沸点和相对密度的函数，其具体的关系式如下：

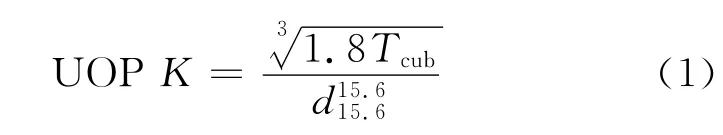
式（1）中，Tcub为立方平均沸点，K；为15.6℃时油品的密度与水的密度的比值。

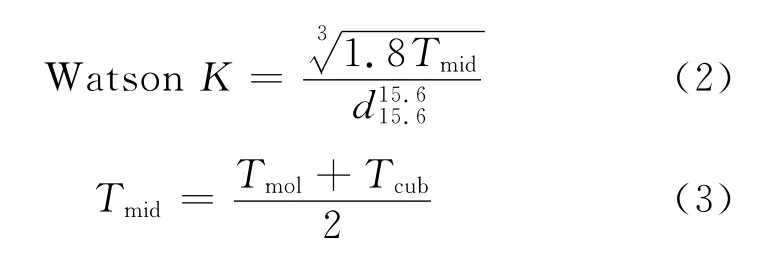
式（2）中，Tmid为中平均沸点，K；Tmol为分子平均沸点，K。

特性因数是一种说明催化裂化原料中石蜡烃含量的指标。K值高，原料的石蜡烃含量高；K值低，原料的石蜡烃含量低。但K值在芳烃和环烷烃之间则不能被有效区分。烷烃的K值最大，约为12.7；环烷烃的K值次之，为11～12；芳烃的K值最小，为10～11。原料特性因数K值的高低最能说明该原料的生焦倾向和裂化性能。原料的K值越高，就越易于进行裂化反应，而且生焦倾向也越小；反之，原料的K值越低，就越难于进行裂化反应，而且生焦倾向也越大。所以K值是表征油品化学组成的重要参数，常可用于关联其它物理性质。但对于含有大量烯烃、二烯烃和芳烃的二次加工产物，特性因数并不能准确地表征其化学属性，使用时会导致较大的误差［2－4］。

特性因数的计算方法有两种：一是依据馏程和密度的分析数据，由公式（1）和公式（2）再结合诺谟图查图计算；二是根据相对分子质量和密度的数据由经验关联式计算。由于在日常生产过程中，对原料通常只进行密度、残炭以及馏程等常规项目的分析，给催化裂化特性因数K值的计算带来困难。

本课题从催化裂化工业装置原料的日常分析数据（通常只有密度、残炭以及馏程）出发，提出催化裂化原料特性因素的计算式，以便于科研、设计及生产部门快速准确地了解装置所加工原料的性质。

1 基于馏程和密度的特性因数计算方法

根据馏程分析数据，按照式（4）计算体积平均沸点tvol。

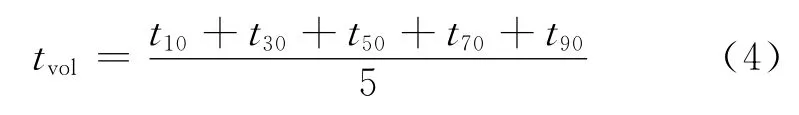
式（4）中，t10，t30，t50，t70，t90分别表示馏出体积分数为10%，30%，50%，70%，90% 时 的 馏 出 温度，℃。

由式（5）计算馏程曲线的斜率。

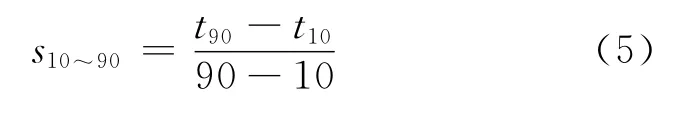
根据式（4）计算出体积平均沸点tvol后，采用诺谟图，由10%～90%馏程直线斜率s10～90查出该斜率所对应的相对于体积平均沸点的校正值tcal，然后按照式（6）计算平均沸点。

式（6）中，ti是泛指平均沸点，可以分别表示分子平均沸点、中平均沸点、立方平均沸点或质量平均沸点，℃。

由式（1）和式（2）可知，要计算特性因数 K值，关键是求出平均沸点。虽然由馏程数据得到10%～90%馏程直线斜率后可以查阅诺谟图得到各平均沸点的校正值，但是该方法并不方便，尤其在编制催化裂化计算模拟软件时不利于计算机自动处理。为此，根据诺谟图中的曲线提出如式（7）所示的计算体积平均沸点校正值tcal的关系式。

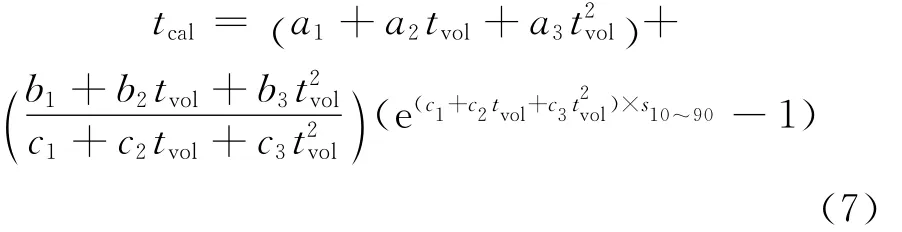
由式（7）可见，平均沸点的校正值被关联成体积平均沸点和10%～90%馏程直线斜率的函数。式（7）中a，b，c等参数表示校正系数，对于不同的平均沸点其值不同，其具体数值可以从诺谟图中的数据关联得到，分别列于表1。

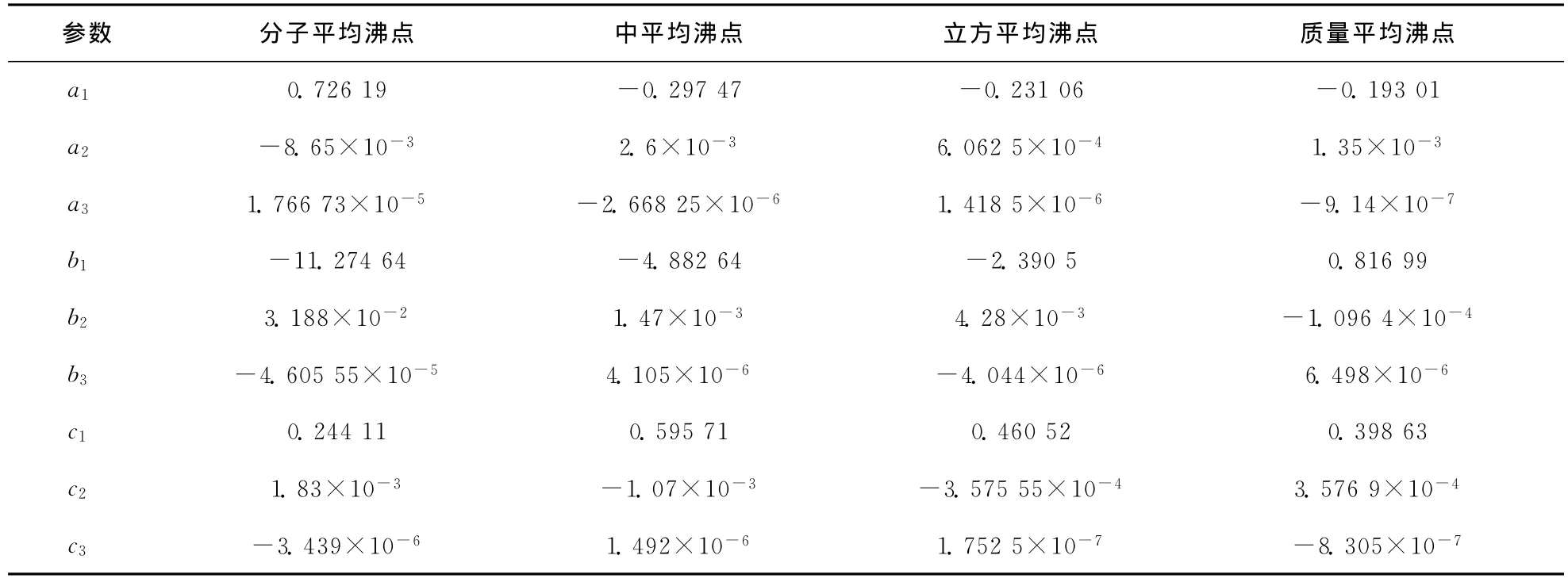
表1 平均沸点校正系数

通过一个实例对平均沸点的计算进行验证，表2为原料馏程，表3为平均沸点验证结果。由表3可见，式（6）和式（7）的计算精度较高，相对误差小于1.5%。

表2 原料馏程

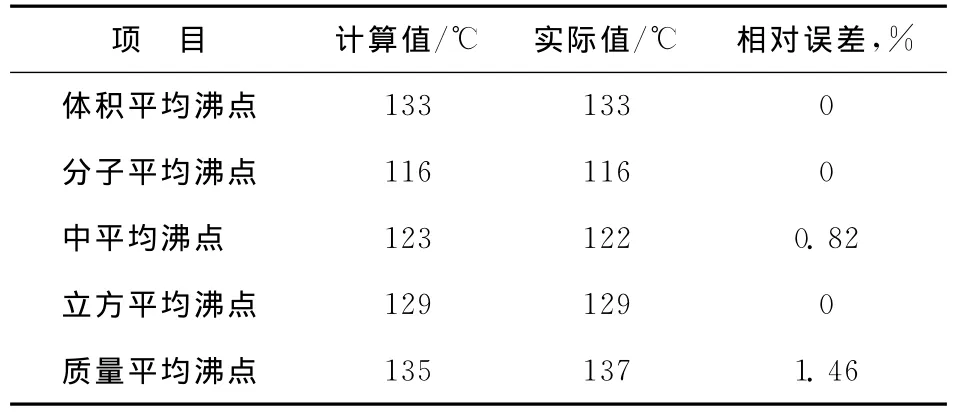
表3 由式（7）计算得到的原料平均沸点结果

根据原料的馏程数据，由式（6）、式（7）可以计算出平均沸点，对于UOP K值，选择立方平均沸点，对于Watson K值选择中平均沸点。计算特性因数K值时，除了平均沸点之外，还需要原料的密度。通常炼油厂分析数据提供的是20℃的密度，而特性因数K值需要15.6℃（即60℉）条件下的密度，为此需要将20℃的密度换算成15.6℃的密度。

原料的密度与温度有着密切的关系，根据不同温度下的原料密度数据［5］，关联出原料密度与温度的变化关系式：

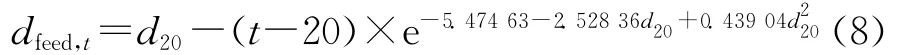
式（8）中，t表示温度，℃；dfeed表示原料的密度，g／cm3。

以某MIP装置的原料性质标定值为例，利用上述计算式对该原料的特性因数进行计算，结果见表4。由表4可见，计算出的UOP K值为11.74，Watson K值为11.72，二者十分接近。由此可见，该原料油可定性为环烷基原料油。

表4 某MIP装置的原料性质及特性因数计算值

2 基于10%馏出温度和密度的特性因数计算方法

根据式（1）或式（2）的特性因子计算式，已知原料的密度和平均沸点就可以计算出特性因子。由于催化裂化原料通常密度较大，大多数情况下并不能得到完整的馏程数据。文献［2］报道用原料的平均相对分子质量和20℃下的相对密度对立方平均沸点进行计算，如式（9）所示。

式（9）中，M表示原料的平均相对分子质量。

利用式（9）计算原料的立方平均沸点时，需要原料的平均相对分子质量测量值，该值在炼油厂催化裂化装置日常生产分析中几乎不进行测试，所以式（9）的应用受到限制。但是，在炼油厂催化裂化原料的常规分析项目中，可以得到10%馏出体积时的温度。本课题由原料的密度和10%馏出体积下的温度（t10）回归出立方平均沸点的计算式，进而根据式（1）计算特性因子UOP K值。立方平均沸点的计算式如式（10）所示。

根据11套催化裂化装置的原料数据，采用式（7）、式（9）以及式（10）进行立方平均沸点计算并进行比较，结果见表5。

表5中立方平均沸点的实测值指的是利用式（7）计算得到的结果，因为该值与诺谟图查得的值非常接近。如果取相对误差的绝对值，式（10）的平均相对误差为1.59%，而式（9）的平均相对误差为2.89%。从相对误差绝对值的范围来看，式（10）的相对误差绝对值在0.04%～3.56%之间，而式（9）的相对误差绝对值范围则为0.97%～5.76%。由此可见，在不能得到完整的馏程数据时，本课题提出的计算式（10）的精度高于式（9）。

表5 不同方法得到的催化裂化原料的立方平均沸点计算结果

3 结 论

（1）根据诺谟图的数据关联出质量平均沸点、分子平均沸点、立方平均沸点和中平均沸点的计算式。计算结果与诺谟图的数值非常接近，在已知原料完整馏程的条件下，完全可以替代诺谟图。

（2）根据原料密度以及10%馏出体积时的温度关联出分子平均沸点的关系式，用于计算特性因子UOP K值。该关联式的计算结果与实际值的相对误差小于4%。

（3）提出了原料密度与温度的关系式，该关系式不仅可用于特性因数的计算，而且可用于催化裂化工业装置标定时原料流量的快速计算。

［1］US－ASTM.UOP Method 375—2007.Calculation of UOP characterization factor and estimation of molecular weight of petroleum oil［S］.2007：1－14

［2］陈俊武.催化裂化工艺与工程［M］.2版.北京：中国石化出版社，2005：400－488

［3］曹汉昌，郝希仁，张韩.催化裂化工艺计算与技术分析［M］.北京：石油工业出版社，2000：33－60

［4］林世雄.石油炼制工程［M］.3版.北京：石油工业出版社，2000：63－107

［5］梁文杰.石油化学［M］.北京：石油大学出版社，1995：98－102