基于循环取货模式的车辆路径优化研究

张利城，吴金卓，何 荣

（东北林业大学工程技术学院，哈尔滨 150040）

循环取货（Milk－run）是一个优化的物流系统网络，用于单个产品或零部件供应商的供应量不能满足指定运输车辆的额定容积并且在该供应商附近还有其他供应商存在的情形。这种取货模式的显著优点是能够满足小批量多频次的要货，并且能够确保运输车辆达到一定的装载率。以整车制造厂零部件入库为例，循环取货的运作方式是车辆根据预先设定好的路线，从整车厂出发，按次序到多家供应商处提货，最后返回整车厂的区域分发中心（RDC）。这样既提高了运输车辆的装载率，又能使物料得到及时供给，同时供给量较少的供货商也不必等到零部件积满一卡车再发运，在最大程度上实现JIT供给。在Milk－run中，车辆路径设计是运输效率的决定性因素，因此，取货车辆的路径优化至关重要，属于车辆路线问题（VRP）。

车辆路线问题（VRP）最早是由Dantzig和Ramser于1959年首次提出［1］，其目标就是在客观条件的约束下，既能满足客户的需求，又能实现总成本最低、时间最短等目的。研究车辆路线问题具有很高的社会和经济价值，因此，该问题自提出以来一直备受人们的关注，并不断发展。学术界对于该问题的研究也取得了大量的成果［2］。在国外，对VRP的研究已经比较深入了，并在企业的Milkrun中得到了很好的应用。国内虽然以上海通用为代表的汽车企业已经从Milk－run中获益，但对于Milk－run车辆路径优化的理论研究还有待进一步完善。本文以国内一家著名的汽车物流企业实际情况为背景，对其零部件循环取货的车辆路线进行优化设计。针对其Milk－run模式建立相应的数学模型，并运用蚁群算法进行优化求解。

1 数学模型的建立

1.1 模型描述

基于循环取货的车辆路径优化的数学模型可以描述如下:物流公司C负责将汽车制造商F的需求零部件用m辆汽车，从RDC出发依次经过Milk－run路线中的n个供应商，最终把货物取回送到RDC。对取货车辆的约束包括:必须在T时间内把货物取回，并且满足车辆最大容积限制。要求车辆在尽可能满载、实现上述约束条件的前提下，寻求物流模式总成本最小的取货路线。这里的总成本包括运输成本、库存成本以及缺货成本。

1.2 模型的目标函数

基于循环取式的车辆路径优化以总成本最小为目标，这里的总成本包括运输成本Z1、库存成本Z2以及缺货成本Z3。很明显，三者在企业实际运营中所占的权重是不一样的。通过引入各个成本的权重w1、w2、w3，可将多目标函数转化为单目标函数得:

（1）运输成本。假设单位货物运输费用与距离成线性关系，即cij=a·dij+b，其中a，b为相关的参数。则运输成本可以表示如下:

式中:nk表示第k条路线的供应商数;dij表示供应商与j的距离;kf表示该供应商在k线路中顺序为f。

（2）库存成本。所有线路上供应商的零部件库存总成本可以表示如下［3］:

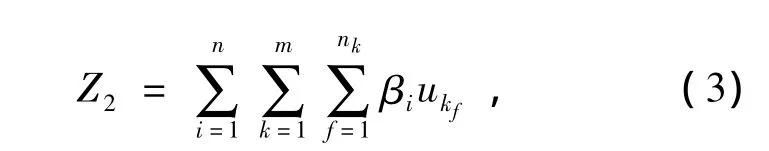
式中:βi为供应商i的零部件单位库存成本;ukf表示路线k上供应商f的零部件的供应量;总路径为m条。

（3）缺货成本。如图1所示，一旦供应商J供货不足，损失函数dj（t）快速上升，当运输车辆在时刻tj［1］到达，断货停止，损失开始下降。在 （0，tj［1］）时间，缺货损失成本仅为损失函数dj（t）=kjt2j;kj为缺货损失函数参数;在 （tj［1］，t）时间段内，缺货损失成本为损失函数和补货函数的差值，即为dj（t） －Rj（t），其中补货函数可以表示如下［4］:

式中:Oj为补货函数参数，这两个参数根据历史数据确定。

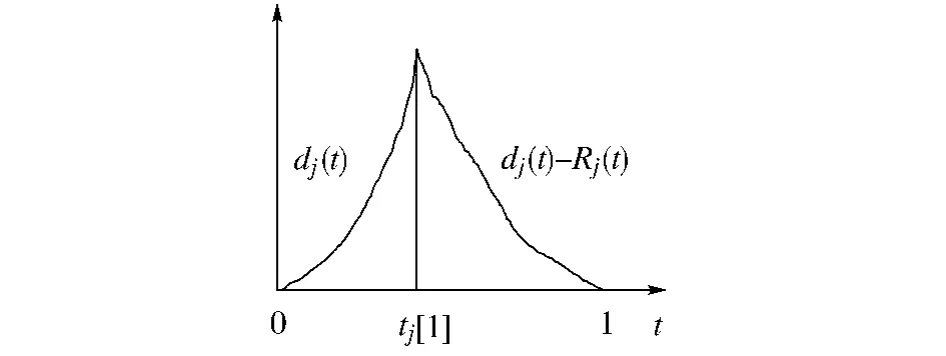
图1 缺货损失函数与补货函数示意图Fig.1 Out of stock function and supplement function

则目标函数为以上3项成本的总和，即:

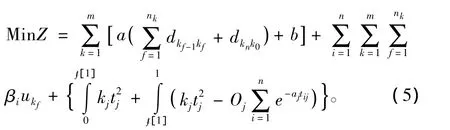
1.3 约束条件

由于现实情况中的约束条件十分繁杂，这里简化起见，只选择其中最重要的两个约束条件，即时间约束和容积约束。

（1）时间约束。

式中:V为n个供应商点与RDC的集合，i=0代表RDC;ti为供应商i的装卸货时间;tij为供应商i到j的行驶时间;T为每次取货总的时间限制;xijk和yik表示如下:

（2）容积约束。假设各种零部件由同一种标准箱包装，零部件的载重量不应超过汽车载重限制，则容积约束如下:

式中:ukf表示用体积表示供应量;Qk为每辆汽车的容积装载上限。

2 数学模型的求解

拟采用“先分组再排路线”的二阶段求解方法，进行取货路线的安排，也就是先将所有的零部件供应商进行分组，然后再对每一组集中的供应商做最优化路线的处理，换句话说，是将车辆路径问题（VRP）转换成多个旅行商问题（TSP），然后运用蚁群算法优化求解。

2.1 构造初始解

先采用系统聚类法按照供应商的地理位置、零部件特性对供应商进行聚类。然后以“车辆装载体积限制”为约束条件，对供应商供应量之和大于车辆装载体积的组进行调整［5－6］。具体调整步骤如下:

（1）以第一组中离RDC最近的供应商为起点进行扫描，然后找到离其最近的供应商，依次进行，直到该组达到了车辆的装载上限，则返回RDC，完成了一条Milk－run线路的构造。

（2）将第一组中剩余的供应商归入第二组，然后按照步骤1对第二组的供应商进行线路构造。

（3）当所有组都构造完路线后，则将最后剩余的供应商依照约束条件再分组，直到所有供应商都被纳入到规划的线路中即完成初始解的构造。

2.2 蚁群算法求解优化路径

由于上一阶段已经将VRP问题转换为TSP问题，因此，接下来只需对TSP进行求解。TSP的求解是NP－hard问题，本文采用蚁群算法进行求解。蚁群算法的提出是受到蚂蚁觅食行为的启发，属于启发式算法。它在求解NP难题中有强大的寻优能力［4］，蚁群算法求解 TSP 的步骤如下［7］:

首先，将m只蚂蚁随机放置在n个城市，位于城市i的第k只蚂蚁选择下一个城市j的概率为:

式中:τ（i，j）为边 （i，j）上的信息素浓度;η（i，j）=1/d（i，j）是启发信息;dij为城市i和j之间的距离;α和β为信息素与启发信息的相对重要性;tabuk为蚂蚁k已经访问过的城市列表。

当所有蚂蚁完成周游后，按公式 （11）、（12）进行信息素更新。

式中:ρ为小于1的常数，表示信息的持久性。

式中:Q为常数;lk为第k只蚂蚁在本次迭代中走过的路径;Lk为路径长度。程序实现框架如下。

（1）初始化。随机放置蚂蚁，为每只蚂蚁建立禁忌表，将初始节点置入禁忌表中。

（2）迭代过程。

3 实例验证

3.1 算例背景

某第三方物流企业专门为汽车制造商提供服务，其零部件物流业务规模非常大，负责制造商的循环取货代理执行，主要包括路线规划设计、取货窗口时间确定，车辆安排调度等。近年来，循环取货模式在该公司入厂物流业务方面虽然得到了广泛的应用和发展，但是发现目前物流运作成本仍然偏高。因此，可以采用本文提出的Milk－run路径优化方法，进一步削减该公司的运营费用。该公司所承担某订单的零部件供应商位置坐标、供应商的供应量见表1，供应商分布图如图2所示。

表1 供应商的位置和零部件供应量Tab.1 The location of suppliers and quantities of parts supply

图2 供应商空间分布Fig.2 Spatial distribution of suppliers

3.2 算例求解

根据该公司所在地车辆统一化标准，物流运输车辆主要采用12 m长东风货车，其最大容积为61 m3。首先，依据系统聚类算法对供应商进行分组，所有供应商的零部件供应总量为335 m3，因此，先将所有供应商分成5个小组。分组信息如下:供应商4、8为第一组;5、7、13为第二组;6、12、14、15、18 为第三组;1、2、3、9、10、16、17为第四组;11、19、20为第五组。各组别供应总量见表2。

表2 初步分组结果Tab.2 Initial grouping results

第一、二组的供应总量小于给定货车的容积上限，因此不必调整。其余三组按照设计好的算法进行调整，调整后的分组结果见表3。

表3 供应商分类结果Tab.3 Classification of suppliers

3.3 循环取货路径优化

利用蚁群算法求解路径优化问题时，首先要对启发式因子α、期望启发因子β、信息素挥发因子ρ进行赋值。Dorigo［8］在求解TSP问题时，推荐参数的最佳设置为:α=1，β=5，ρ=0.5。

经过计算，得各循环取货小组运输路线安排如下，其中第二个循环取货小组的路径优化结果如图3所示。图中点a（b）的a表示供应商序号，b表示该供应商的零部件供应量。

图3 旅行商问题优化结果Fig.3 Optimization results for TSP

优化的结果只能确定各供应商间的取货相对顺序，而无法确定起止位置，企业必须结合实际情况加以选择。各组优化的参考路线见表4。由表4可以看出，优化结果满足装载率较高的要求。另外，还可以实现路径距离的优化。其中线路2的原路线距离为0.815 4，优化后最短路径为0.745 8，节省了8.5%。由此可见，蚁群算法的结果明显优于手工排定的线路。

表4 路径优化结果Tab.4 Route optimization results

4 结束语

本文在分析了循环取货的特点后，建立了其车辆路径的数学模型，构造了先将规模较大的VRP转换为多个相对小规模的TSP，然后再用蚁群算法优化求解的的算法，在一定程度上降低了循环取货车辆路径问题的复杂程度。最后，给出了一个实际算例验证了优化算法的可行性和准确性，为企业进行循环取货车辆路径规划提供了有效参考。

】

［1］Toth P，Vigo D.The Vehicle Routing Problem［M］.Society for Industrial and Applied Mathematics，Philadelphia:SIAM，2002.

［2］王 旭，陈 栋，王振峰.汽车零部件Milk－run车辆调度优化模型和算法［J］.计算机应用，2011，4（31）:1125 －1128.

［3］汪金莲，蒋祖华.汽车制造厂零部件入厂物流的循环取货路径规划［J］.上海交通大学学报，2009，11（43）:1704 －1708.

［4］曾敏刚，崔增收.基于循环取货的汽车零部件入厂物流优化研究［D］.广洲:华南理工大学，2011.

［5］张 坤，江海容.汽车零部件循环取货车辆路径优化研究［J］.物流科技，2009（2）:69 －72.

［6］王 蕊，邢艳秋，李 洋.饮料配送中心配送量预测与仓储空间评价方法［J］.森林工程，2012，28（5）:107 －109.

［7］段海滨.蚁群算法原理及其应用［M］.北京:科学出版社，2005.

［8］Dorigo M，Maniezzo V，Colorni A.The ant system:optimization by a colony of cooperating agents［J］.IEEE Trans.System，Man，AND Cybernetics-Part B:Cybernetics，1996，26（1）:29-42.