求解二维弹性半空间散射问题的波函数组合法①

姚 虞，刘天云，张建民

（清华大学水沙科学与水利水电工程国家重点实验室；清华大学土木水利学院，北京 100084）

0 引言

地震波在传播的过程中由于行波效应和相干效应，震动场各处的地震动在幅值和相位上均有差异。不规则地形各点的动力响应应为入射波与散射波作用的叠加。对于大型结构，如高坝或大型地下结构等，地震波输入的非一致性不可忽略，而这是目前一般计算所采用的一致性输入方式所不能考虑的。此外，对于动力有限元计算，如何处理人工边界的反射问题也是一大难点，主要有全局人工边界和局部人工边界两类［1］。全局人工边界有边界元法、波函数展开法、基于惠更斯原理的方法等；局部人工边界通常采用粘性或粘弹性边界、透射边界等。然而各种人工边界也有相应的问题，如全局人工边界中边界元法的奇异性问题［1］，波函数展开法无法满足半空间无限自由表面零面力条件等［2］；又如局部人工边界中粘性边界的低频失稳问题［3］，粘弹性边界对面波的吸收效果差［4］的问题等。本文提出一种满足全局边界条件的的波函数组合方法，可以考虑包括瑞利波在内的不同地震波的不同角度入射情况，是一种精确的非一致位移输入方式。以往的方法是本文方法的近似解。

1 问题描述与波动方程

对二维半空间内任意边界形状的空心体，在地震波作用下我们希望求得其边界各点的地震动响应以作为空心体内部结构动力有限元计算的地震动输入。图1是表示瑞利波或任意角度的压缩波或剪切波入射到二维半空间不规则河谷的示意图。要求解的问题是在任意平面波的作用下河谷边界任意一点的震动过程。若能求解不规则河谷任意一点的震动过程，则该解可作为河谷内土石坝地震动响应有限元求解的输入。

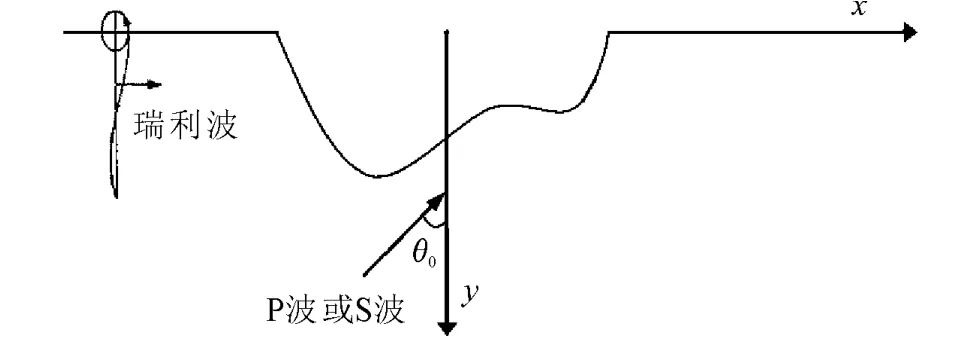
图1 二维半空间不规则河谷入射波示意图Fig．1 Incident wave of 2Dirregular valley in half space

本文提出的求解该类问题的方法称为波函数组合法，是将体波波函数与瑞利波波函数组合而成的新方法。其中波函数是位移势函数表示的波动方程的通解。

任何一个矢量场可以分解可为一个无旋场（梯度场）和一个无散场（旋度场）之和：

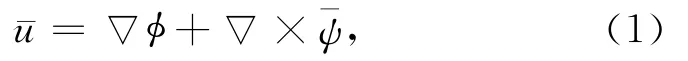
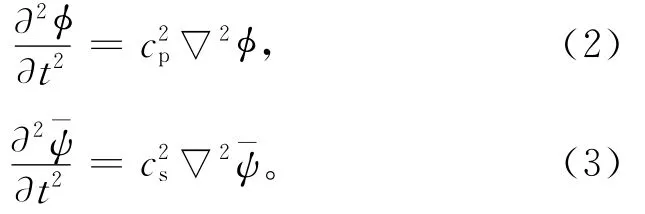
在频域内，对于单一频率的波，方程（2）和（3）的解和写为分离变量的形式，即

将式（4）和（5）带入式（2）和（3），可得

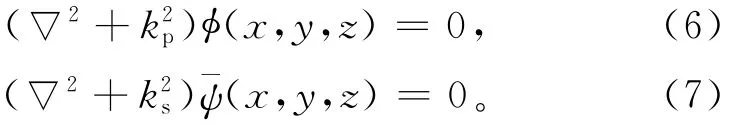
式（6）和（7）称为亥姆霍兹方程，是频域内波动方程。

对于二维问题，矢量势的三个分量都与x3无关，则式（1）写成分量形式为

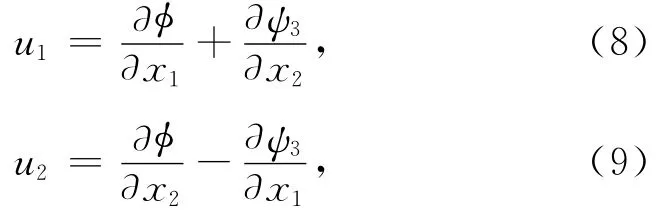
为简单起见，记ψ3为ψ，则对于二维问题方程（3）可转化为

即位移场由φ和ψ两个位移势函数决定。

2 二维半空间波函数组合法

二维半空间的波函数组合法是将二维全空间的波函数展开法与二维半空间的Lamb解组合，以同时满足散射边界零面力边界条件和半无限空间自由表面的零面力条件。其基本思路是：

（1）确定入射波自由场应力；

（2）位移、应力柱波函数展开；

（3）确定自由表面柱波函数产生的面力；

（4）在半无限空间自由表面反向叠加柱波函数产生的面力，应用Lamb基本解计算散射边界次生面力；

（5）匹配散射边界处自由场面力、波函数产生的面力与Lamb基本解产生的面力，形成散射边界无面力状态。

2．1 柱波函数展开法

在极坐标中方程（2）和方程（10）有如下分离变量形式的一般解：

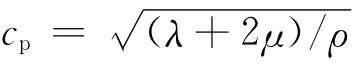
极坐标下式（8）和式（9）转化为

再由几何方程和广义胡克定律，可得三个应力分量的表达式为

将式（11）和式（12）带入式（13）至式（17），可以得到用组合系数An和Bn表达的位移场和应力场。

2．2 波函数组合法

图2 自由表面残余面力的消除Fig．2 Elimination of residual stress on free surface

将虚拟面力进行Fourier变换为P（k）与Q（k）：

对于表面激励荷载，可利用瑞利波的位移势函数求解［6］。设瑞利波势函数为

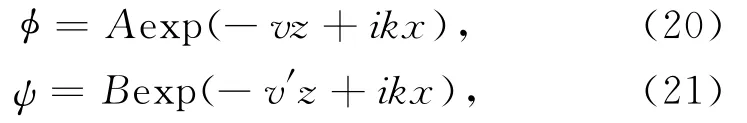
其中v2＝k2－α2，v′2＝k2－β2，且0≤arg（v）≤π，0≤arg（v′）≤π。则在x－z坐标系下，位移与应力分别为

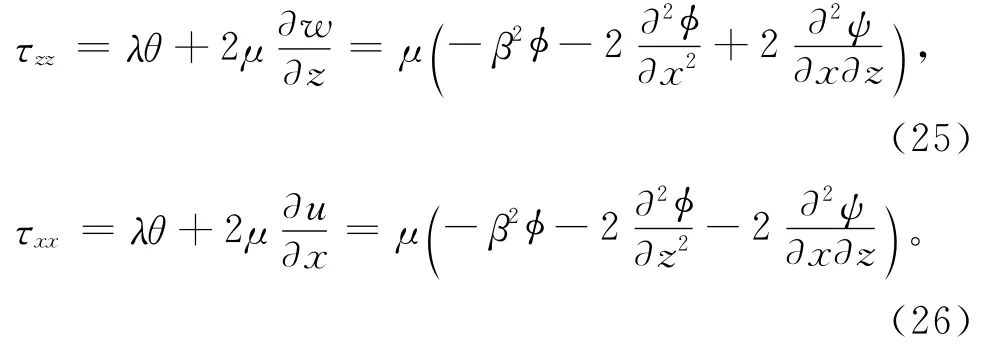
由瑞利波势数得到的应力位移场是单一频率的，因而一般解应该要对波数积分，即

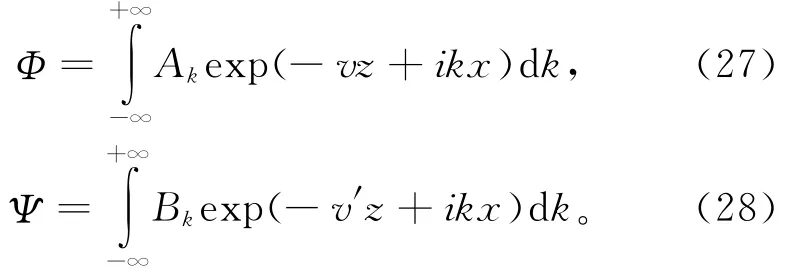
应力场和位移场也为相应的形式。而对需要在自由表面施加的空间域的面力，可写为波数域的逆变换形式，即

需要在自由表面出满足的零面力条件为

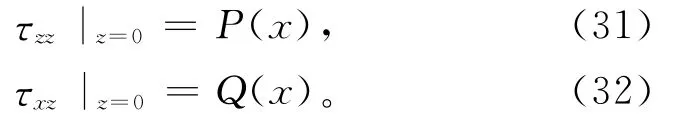
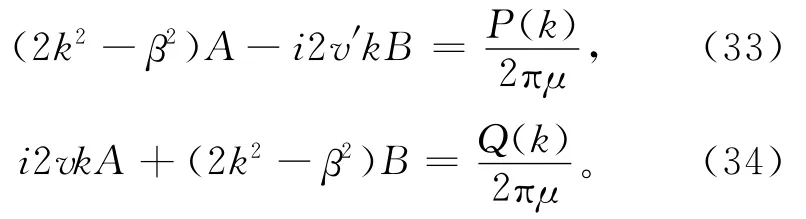
由式（33）和式（34）可将A、B用组合系数An和Bn表达，则Lamb解产生的应力场和位移场均可由An和Bn表达。

全空间的波函数展开法叠加上Lamb解之后，水平自由表面的零面力条件自动满足，且散射场可由An、Bn表达。由河谷边界的零面力条件可以确定组合系数An、Bn，进而确定散射场。

3 算例及应用

对半圆形河谷的散射问题，编写MATLAB程序进行了验证。算例包括对不同频率和入射角度的P波、SV波以及不同频率的R波入射情况的验证。

验证结果所参考的文献为H．L．Wong在1982年发表的文章［7］。该文章给出的结果已被Francis－co等人作为验证其计算结果的参考［2］，因而相对可靠。当然，Wong的方法本身不稳定，按文献［2］所说及笔者编程序验证，其计算结果随激励作用源的变化而变化。而Francisco等人的方法对R波的计算结果也不好［2］，经笔者编程验证是随自由表面延伸长度而改变的。这也体现出本文方法的优点所在。

经过计算，文献中所给出的半圆形河谷的28个结果均得到验证，现给出部分结果对比图。

图3给出的是P波入射时半圆形河谷边界的水平和竖向位移的放大系数图。图中横坐标为边界点坐标x与河谷半径R的比值；纵坐标为位移幅值与入射波位移幅值的比值，即放大系数；其中水平方向放大系数用｜ux｜表示，竖直方向放大系数用｜uy｜表示；θ表示入射方向与竖直方向的夹角；η为无量纲频率，表征相对于河谷尺度的入射波波数的大小，表达式为

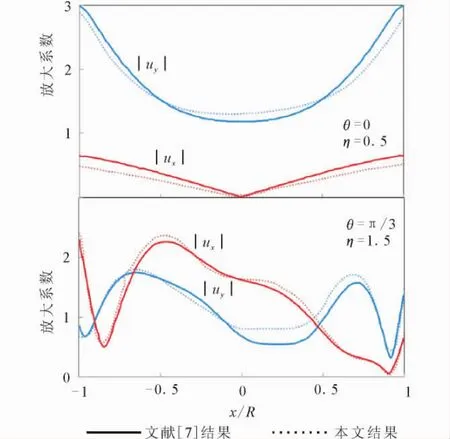
图3 P波入射河谷边界位移放大系数比较Fig．3 Comparison of displacement amplification factors of valley boundary under incidence of P wave

同样，图4和图5分别给出了SV波和R波入射时的情况。可以看出，本文的方法作为理论上的精确解，计算出的结果与文献［7］给出的结果是大体一致的。这一方面是对本方法所编写程序的验证，另一方面说明文献［7］在适当的激励作用源分布下可以得到正确的结果。但是由于没有确定激励作用源分布的方法，所以文献［7］的方法的不稳定限制了其实用性。而本文提出的波函数组合法则不存在这样的缺陷，并且由于引入快速傅里叶变换解决半空间自由表面应力问题，避免了大量无穷积分的计算，相比之下计算时间要节省很多。

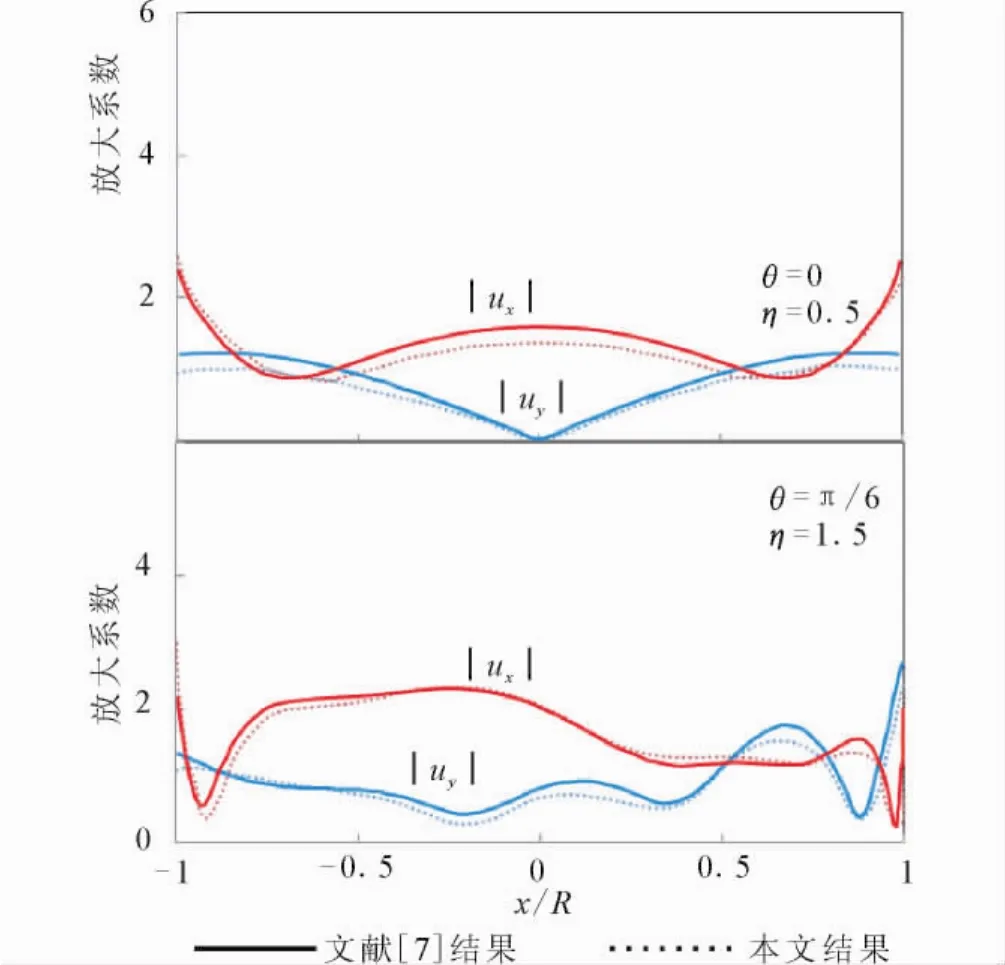
图4 SV波入射河谷边界位移放大系数比较Fig．4 Comparison of displacement amplification factors of valley boundary under incidence of SV wave

图5 R波入射河谷边界位移放大系数比较Fig．5 Comparison of displacement amplification factor of valley boundary under incidence of R wave

基于波函数组合法亦可解决三维不规则地形散射问题，限于篇幅，将另文介绍。

4 结论

本文提出的二维波函数组合法可以解决二维半空间内任意空心体的散射问题。程序经半圆形河谷散射问题验证，对P波、S波和R波入射情况均能得到合理结果。相比于已有方法，本方法在数值上是稳定的，在理论上是完备精确的。

［1］ 廖振鹏．工程波动理论导论（第二版）［M］．北京：科学出版社，2002．

LIAO Zhen－peng．Introduction to Wave Motion Theories in Engineering［M］．Beijing：Science Press，2002．

［2］ Francisco J Sanchez－Sesma，Miguel A Bravo，Ismael Herrera．Surface Motion of Topographical Irregularities for Incident P，SV，and Rayleigh Waves［J］．Bulletin of the Seismological Society of America，1985，75（1）：263－269．

［3］ LIU Jing－bo，LU Yan－dong．A direct Method for Analysis of Dynamic Soil－structure Interaction Based on Interface Idea［A］／／ZHANG Chu－han，WOLF J P．edit．Dynamic Soil－Struc－ture Interaction［G］．［S．l．］International Academia Publishers，1997：258－273．

［4］ 李彬．地铁地下结构抗震理论分析与应用研究［D］．北京：清华大学，2005．

LI Bin．Theoretical Analysis of Seismic Response of Underground Subway Structures and Its Application［D］．Beijing：Tsinghua University，2005．

［5］ 鲍亦兴，毛昭宙．弹性波的衍射与动应力集中［M］．北京：科学出版社，1993．

PAO Yih－Hsing，MOW Chao－Chow．The Diffraction of Elastic Waves and Dynamic Stress Concentrations［M］．Beijing：Science Press，1993．

［6］ ［美］阿肯巴赫，著．徐植信，洪锦如，译．弹性固体中波的传播［M］．上海：同济大学出版社，1992．

Achenbach J D．Translated by XU Zhi－xin，HONG Jin－ru．Wave Propagation in Elastic Solids［M］．Shanghai：Tongji Univerity Press，1992．

［7］ H L Wong．Effect of Surface Topography on the Diffraction of P，SV and Rayleigh Waves ［J］．Bulletin of the Seismological Society of America，1982，72（4）：1167－1183．