考虑填土侧向变形的地震土压力计算方法①

张建民，宋 飞

（1．清华大学水沙科学与水利水电工程国家重点实验室 清华大学土木水利学院，北京 100084；2．长安大学公路学院，陕西 西安 710064）

0 引言

地震土压力的评价是挡土类结构物抗震设计中的一个基本问题，。日本学者物部和冈部最早基于极限平衡理论和拟静力概念提出的物部—冈部地震土压力公式［1，2］因其概念清晰、方法简便而在工程实践中得到了十分广泛的应用，至今仍是评价地震土压力的主要方法。Morrison和 Ebeling［3］，Kumar［4］，Subba Rao等［5］基于极限平衡理论，用曲面和组合滑动面求解静力和地震荷载作用下的被动土压力，其计算结果较库仑理论和物部—冈部公式更为合理。Kumar和 Chitikela［6］，Cheng［7］根据滑移线场理论对水计算出地震主动和被动土压力系数。Prakash 和 Saran［8］，Prakash 和 Basavanna［9］，Das和Puri［10］在Coulomb土压力理论和物部—冈部地震土压力公式的基础上考虑了填土的粘聚力、墙背和填土之间的粘聚力，以及铅直方向的惯性力对土压力 的 影 响。Chen 和 Liu［11］、Soubra 和 Kastner［12］，Soubra［13］基于极限分析的方法给出了静力条件下和地震作用时的土压力系数的图表。然而，以上方法只能计算主动和被动这两种极限状态下的土 压 力。 Matsuo［14］，Matsuo 和 Ohara［15］，Ishii等［16］，Ichihara 和 Matsuzawa［17］，Sherif 等［18］，Sherif和Fang［19］，Ishibashi和 Fang［20］的地震土压力模型试验结果表明，挡墙的位移量和位移模式对于地震土压力的大小和分布具有很大影响。在实际工程中，大量存在的城市建筑物地下边墙、浅埋结构物、桥墩上所作用的土压力通常是介于主动土压力和被动土压力之间的某一值，能够使得墙后填土达到主动和被动极限状态的墙体位移量通常不会发生。

Seed 和 Whitman［21］，Shakya［22］，Prakash等［23］，Iai［24］，Wu［25］总结了地震作用下挡土结构发生的位移。Psarropoulos等［26］，Maleki和 Mahjoubi［27］采用有限元法计算了挡墙后地震土压力分布，但其计算结果和精度依赖于计算模型和参数的合理选取。试验研究表明，土压力与挡墙位移之间没有唯一性的关系，而是随墙体位移模式和填土的性质等在一个较为宽泛的范围内变化［28］。土压力系数随挡墙位移量变化关系的曲线形状也不唯一。当挡墙发生不同的位移模式时，即使其位移量相等，沿墙高不同深度处的填土的土压力系数也是不同的。Terzaghi［29］的模型试验结果表明，松砂达到主动状态的位移量的数量级约为0．008H（H为挡墙高度），密砂达到主动状态的位移量的数量级约为0．001H；Fang［30－31］的试验结果表明，松砂达到被动状态的位移量的数量级约为0．17H，密砂达到被动状态的位移量的数量级约为0．015H。因此，当挡墙位移量相同时，不同填土的土压力系数相差较大，在一个宽泛的范围内变化。即使对于一定内摩擦角的正常固结土在挡墙平动位移模式下，也未证实土压力系数与挡墙位移量之间具有唯一性关系。

基于作者以往的研究，本文首先拟阐明压剪耦合效应的不同是土压力随应变约束条件变化的原因，采用渐近状态应力比概念反映不同应变约束条件下填土沉积或压密到稳定状态时的土压力系数，指出土压力系数与侧向应变约束条件之间具有唯一性关系、但与挡墙位移量之间的关系则不具有唯一性。其次，基于作者提出的渐近状态准和中间滑楔体概念，给出从主动到被动状态的任意中间状态下的土压力计算公式及算法，并采用试验初步验证了所提方法的合理性。

1 土压力系数与应变增量比之间的唯一性关系

如图1所示，随着挡墙位移量的变化，墙后填土的应变约束条件发生了变化。张建民等［32－33］认为，挡墙位移实质上是导致了墙后填土的应变约束条件发生了变化，从而引起土压力系数的变化。基于这样的认识，他们采用土单元体的应变增量比（小主应变增量与大主应变增量的比值，记为Rε＝Δε3／Δε1）来表述土的应变约束条件。Rε越接近于1，侧向变形与轴向变形越接近，剪切变形越小。而Rε越小，则侧向变形与轴向变形的差异越大，剪切变形越大。

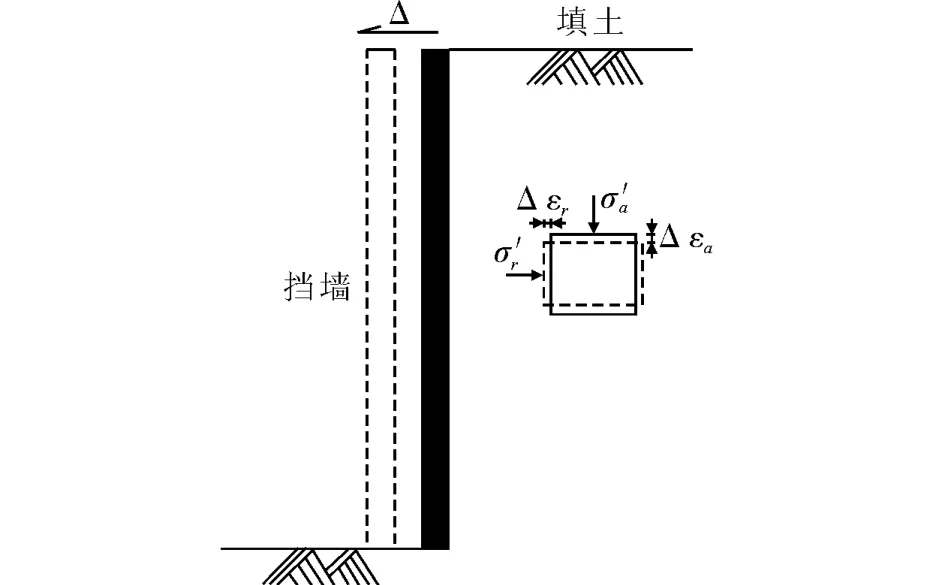
图1 填土的侧向应变约束条件随挡墙位移量的变化Fig．1 Variation of the lateral strain constraint of backfill with the wall displacement．

张建民等［32－33］针对饱和丰浦砂在控制不同常应变增量比条件下进行了应变路径试验（称之为等应变增量比试验），通过这些试验来测定采用不同应变增量比表示的应变约束条件下填土经过沉积或压密达到稳定状态时的不同应力比（称之为渐近状态应力比，其与土压力系数的物理本质相一致）。图2给出了在控制应变增量比分别为0．22、－0．10和－0．42时应力比和轴向应力的关系。

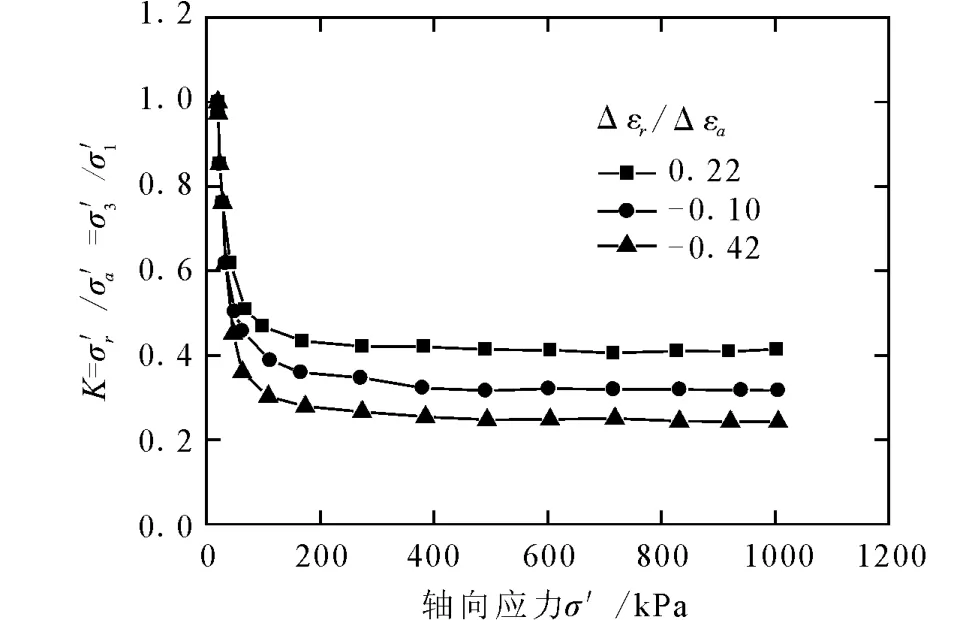
图2 应力比与轴向应力的关系Fig．2 Relation between stress ratio and axial stress．

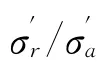
张建民等给出了定量描述上述渐近状态应力比与应变增量比之间关系的数学表达式，即渐近状态准则［28，33］：

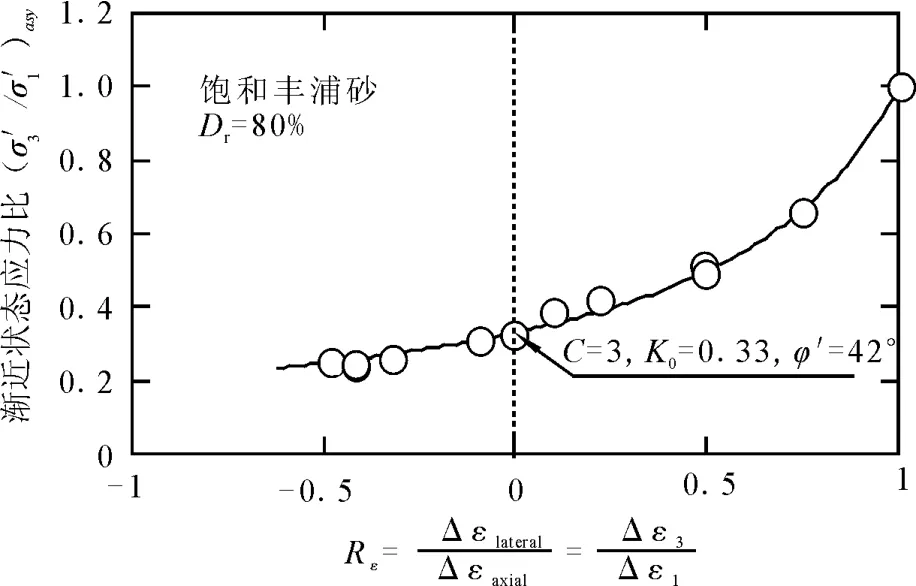
图3 渐近状态应力比与应变增量比的关系曲线Fig．3 Asymptotic stress ratio mobilized along different constant strain increment ratios．

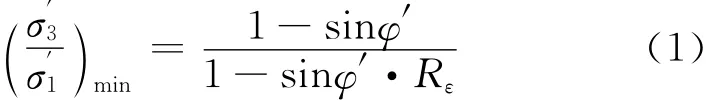
式中的φ′是通过排水的常规三轴压缩试验确定的，Rε＝Δε3／Δε1。

式（1）可拓展为平面应变条件下土压力系数与应变增量比之间关系的数学表达式，其在Rε＝0时成为Jaky公式，在Rε＝－1时成为郎肯主动土压力计算公式，在Rε＝1时其计算得到的应力比值为1，即为各向同性材料在等向压缩状态时的应力比值。基于（1）式以及 Mohr－Coulomb准则可得到土的发挥的内摩擦角与应变增量比有如下的关系［35］：

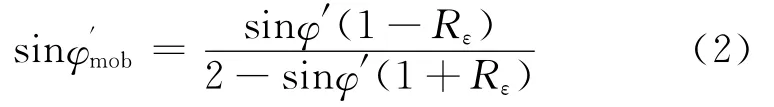
Chu等［35］、张建民等［33］、Asaka等［36］的等应变增量比试验结果均表明，渐近状态所对应的应力比仅与应变增量比有关，与土单元体初始的应力状态、应力路径以及应力应变历史均无关。对于一定φ′值的正常固结土，渐近状态应力比（即土压力系数）与应变增量比之间的关系具有唯一性，二者之间的关系可用（1）式来表述。图4给出了（1）式计算结果与未扰动丰浦砂和悉尼砂的等应变增量比试验结果的对比。通过对比可知，对于内摩擦角一定的各向同性正常固结土，以渐进状态应力比表述的土压力系数和以应变增量比表述的侧向应变约束条件之间的关系均可以用（1）式来唯一表述。对于各向异性砂土，土压力系数与应变约束条件之间的关系也具有唯一性，其研究结果详见文献［37］。

2 侧向应变约束条件对土压力的影响

张建民等［33，38］指出，导致渐近状态应力比随应变增量比变化而变化的内在原因，是加载过程中压缩效应与剪切效应的相对影响程度不断调整的结果，将压缩效应与剪切效应耦合变化的力学行为及其对土的应力—应变响应的影响定义为压剪耦合效应（简称压剪效应），它是土压力形成的物理本质。

图4 渐近状态准则的试验验证Fig．4 Verification of asymptotic state criterion by different constant strain path tests for two sands．

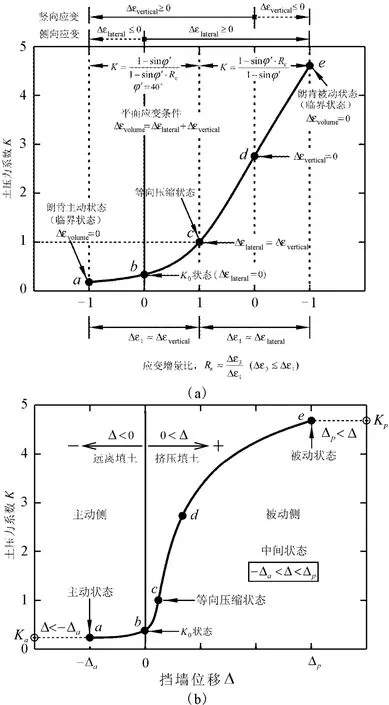
图5 土压力系数随应变增量比及挡墙位移量的变化关系Fig．5 Change of earth pressure coefficient with strain increment Ratio and wall displacement．

基于压剪耦合效应规律及渐近状态准则，张建民等［28，33］给出了土压力系数随应变增量比以及挡墙位移量的变化关系，如图5所示。

从图5可以看出，在平面应变条件下，对于c点，土单元体的Rε，侧向变形等于竖向变形，处于等向压缩状态，如果不考虑各向异性的影响，其应力比值也是1，此时土单元体只具有压缩效应。对于a点和e点，土单元体的Rε，其体应变增量Δεv＝0，此时土单元体分别处于主动和被动极限状态，剪—正应力比达到峰值，剪应力增量为零，剪切变形不断增大，符合临界状态的概念，土单元体仅具有剪切效应。从等向压缩状态到主动与被动状态之间，随着应变增量比的变化，土单元体的压缩效应与剪切效应相互作用的程度不断调整，使得土单元体处于不同的渐近状态，对应着不同的土压力系数与发挥出的土内摩擦角。

挡墙位移量的变化会造成墙后填土处于不同的应变约束条件下，压缩效应与剪切效应相互影响的程度不同，起动的剪—正应力比不同，土的强度发挥不同，作用在挡墙上的土压力也不同。图6和7分别给出了主动侧和被动侧土压力形成的物理机制示意图。

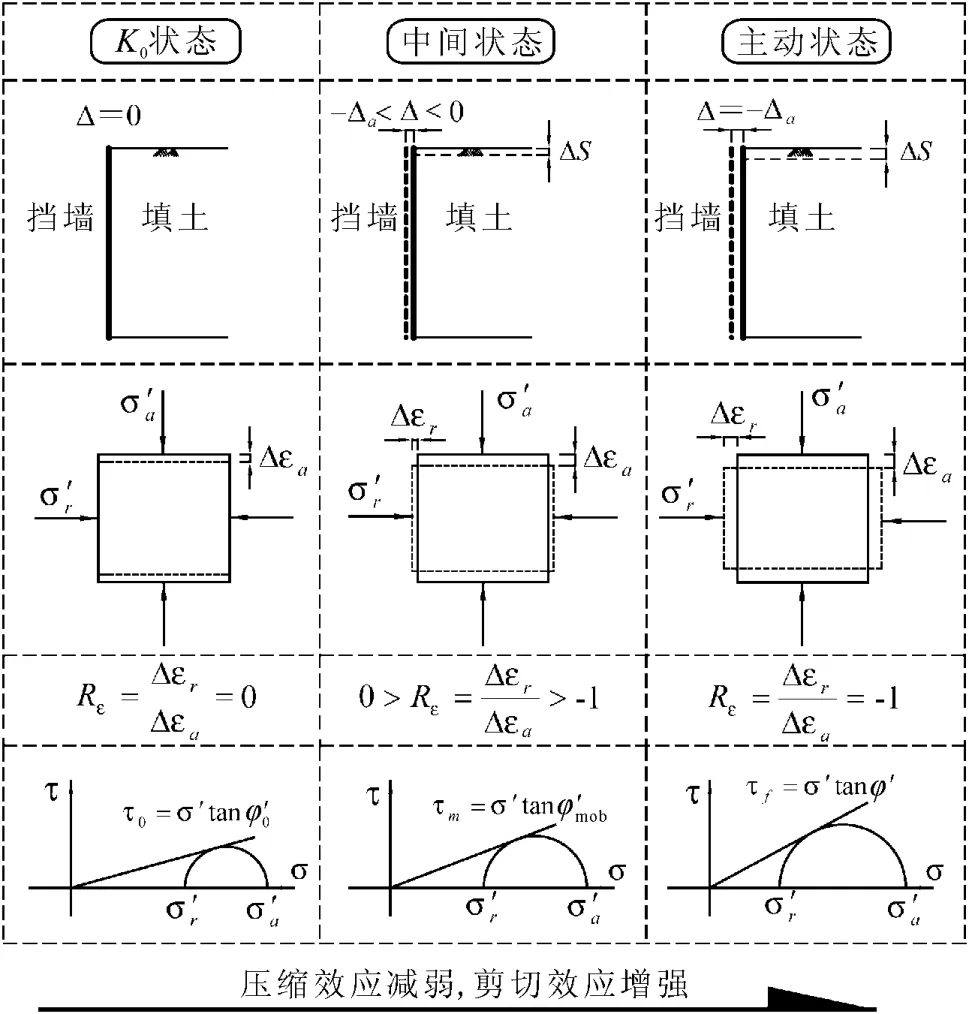
图6 主动侧土压力形成机制Fig．6 Schematic diagram of earth pressure at the active side．

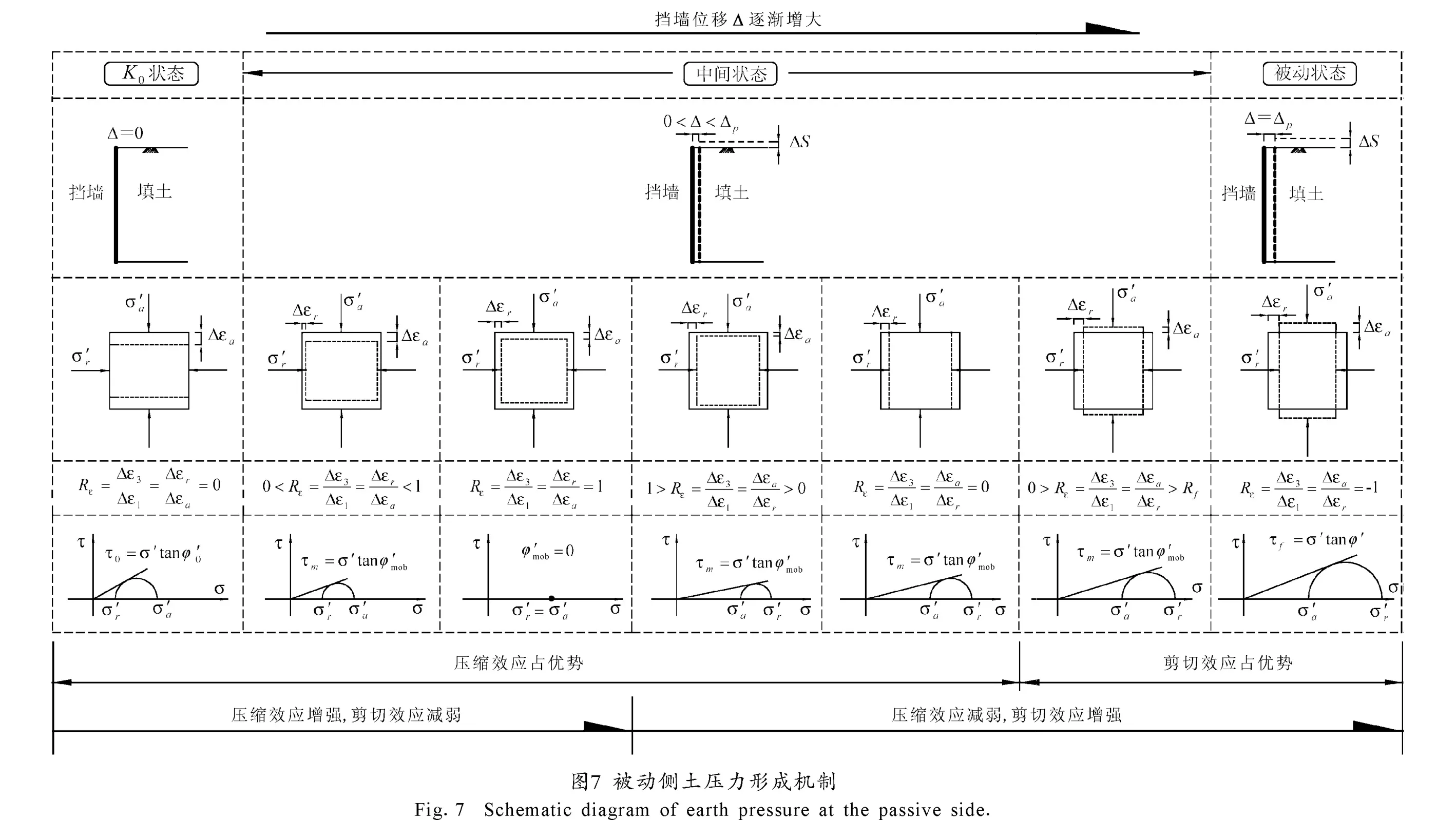
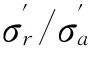
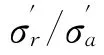
当Rε＝1时，土单元体的侧向变形等于轴向变形。对于各向同性体，只具有压缩效应，其体变只有球应力引起的体缩分量，土压力系数为1，应力圆缩小为一点，土单元体发挥的强度为零；随着挡墙位移量的增大，填土的侧向压缩量和轴向膨胀量进一步增大，剪切变形逐渐增大，Rε从1逐渐减小到0，最终减小到－1。在这一过程中侧向应力在增大到等于轴向应力后继续增大，侧向应力与轴向应力的差距逐渐增大，剪— 正应力比逐渐增大，应力圆面积逐渐增大，砂土的剪切效应逐渐增强，压缩效应逐渐减弱。当Δ＝Δp（Δp为达到被动状态所需的挡墙位移量）时，Rε＝－1，砂土发生剪切破坏，起动的剪—正应力比达到极大值，应力圆再次与Mohr－Coulomb强度包线相切，砂土的强度完全发挥，达到被动极限状态。在Rε＞0的阶段，压缩效应占优势，Rε＜0的阶段，剪切效应占优势。

3 土压力计算方法

如图5～7所示，应变增量比Rε从主动状态到被动状态不是单调变化的，为了表述方便，张建民等［28］给出应变约束参数R用以描述填土的侧向变形，它与Rε的关系如下：

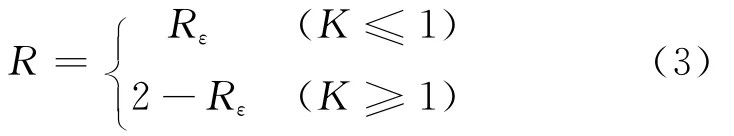
式中K为土压力系数。

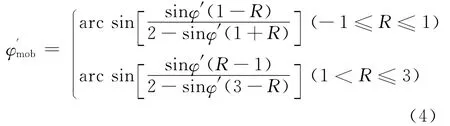
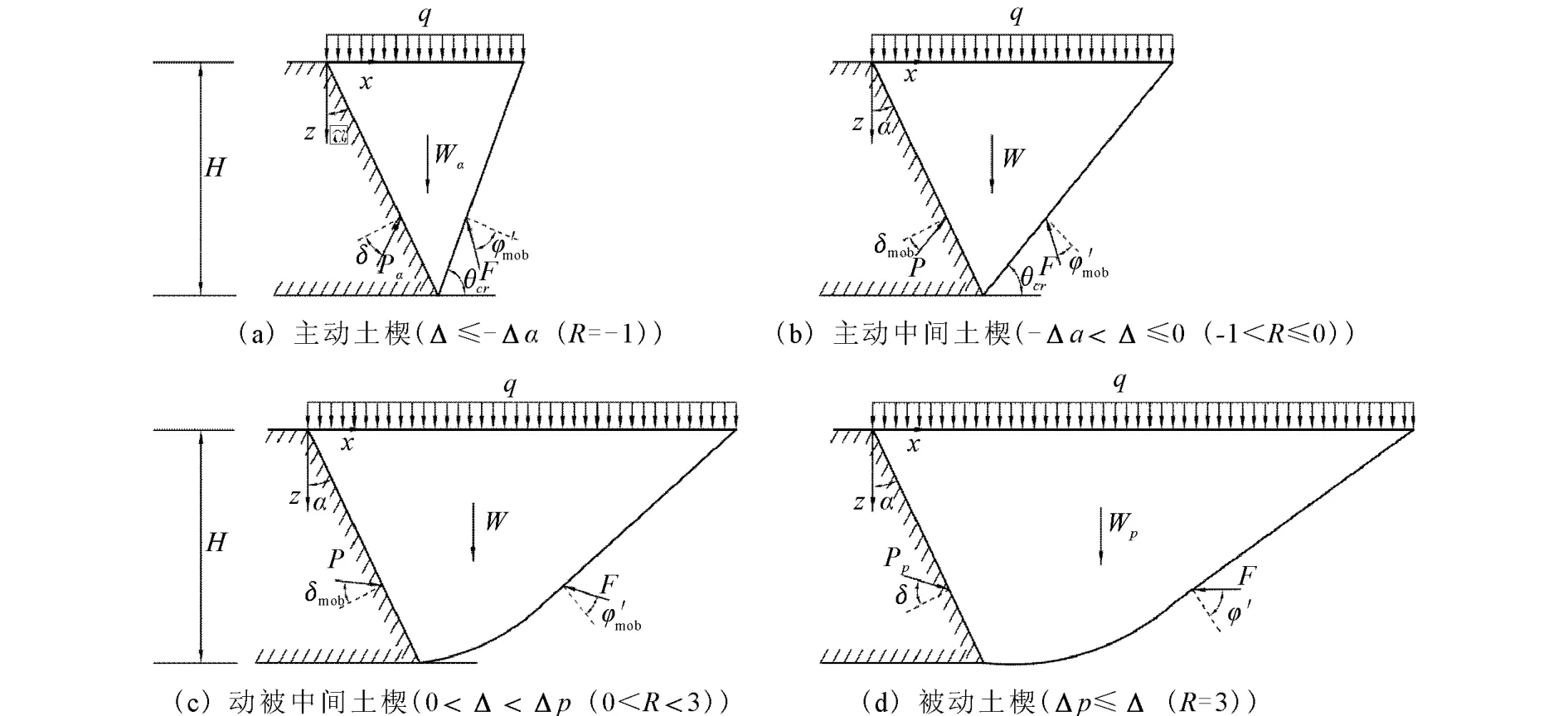
图8 主动、被动及中间土楔示意图Fig．8 Variation in the dimensions and weight of static intermediate soil wedge with lateral wall displacement．

当挡墙远离填土或挤压填土的位移量Δ足够大，Δ＝Δa或Δp时，墙后填土分别处于主动及被动状态时，土的内摩擦角和墙背摩擦角完全发挥，填土中分别形成主动或被动滑楔体。当挡墙位移量使得墙后填土既没有达到主动状态，也没有达到被动状态，而是介于两者之间时，填土的强度以及墙背摩擦角没有充分发挥，存在一个中间滑楔体，中间滑楔体的尺寸取决于应变约束参数R，亦即取决于挡墙的位移量。图8给出了主动土楔、中间土楔和被动土楔的示意图。地震荷载作用下的土压力实质上是在静荷载作用下滑动土楔的平衡力系中增加水平和铅直惯性力的作用根据力的平衡求解得到的。

Terzaghi［39］的研究结果表明，主动侧滑动面为一平面，而在被动侧一侧，当墙背摩擦角较大时，填土中的滑动面通常为一曲面。此时，平面滑动面会过高估计被动侧土压力的大小，造成工程设计偏于危险［39］。如图8所示，主动侧滑楔体的滑动面为一通过墙底的平面；被动侧滑楔体的滑动面为一组合滑动面，靠近墙底部分滑动面为对数螺旋曲面，靠近填土表面部分为一平面。

Sherif等［18，40］的土压力模型试验结果表明，振动挤密会在填土中引起残余土压力，增加土压力的大小。Sherif等［40］建议，在K0状态，由于振动挤密引起的残余土压力系数可由下式确定：

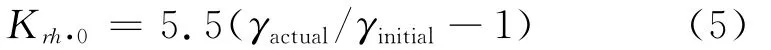
式中γactual为土体振动挤密后的实际重度，γinitial为自重压实土体的重度。并且他的试验结果表明，这部分水平残余土压力沿墙高线性分布［40］。张建民等［32］基于对 Matsuo［14］、Ishii等［16］、Ichihara等［17］、Sherif等［18－19］的土压力试验结果的分析，认为这部分由振动挤密引起的残余土压力也随应变约束条件的变化而变化。在主动及被动一侧，残余土压力系数Krh与应变约束参数h的关系可以由（6）式及（7）式确定：

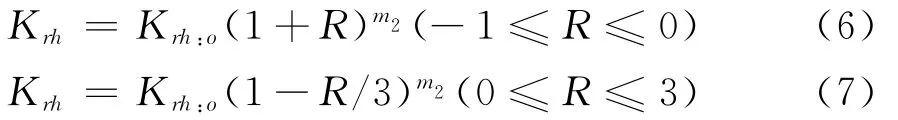
m1和m2由试验确定，可近似取为1。

基于以上的土压力形成机理分析以及中间滑楔体的概念，对滑楔体进行受力分析，可得到中间状态的土压力计算方法：

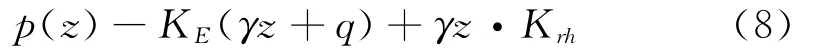
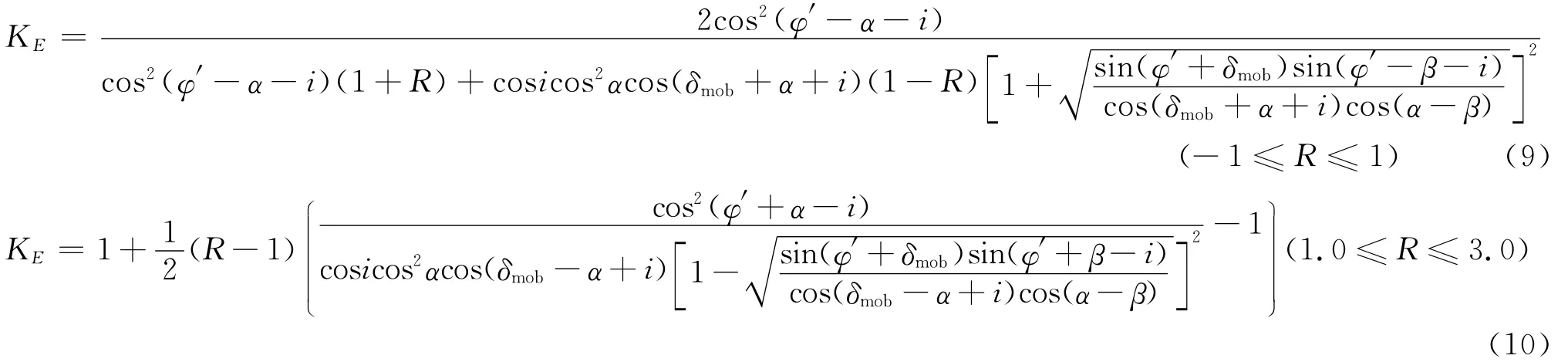
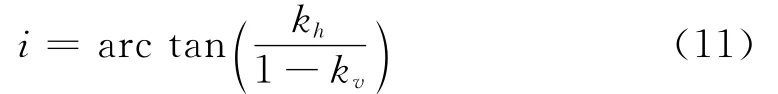
式（8）～（10）中q为填土面堆载；α为墙背倾角；β为填土面与水平面的夹角；φ′为土的内摩擦角；δmob为墙背摩擦角的发挥值；R为应变约束参数；kh和kv分别为水平和铅直方向的地震加速度系数。当R＝0时，（9）式成为动荷载作用时中性状态下的土压力计算公式：

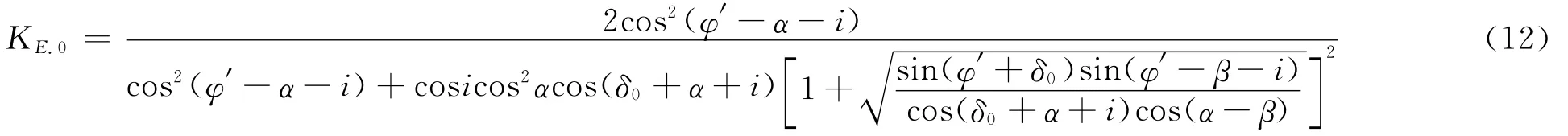
式中δ0为R＝0时的墙背摩擦角发挥值，式（11）当i＝0时进一步退化为静荷载作用下K0状态时的土压力计算公式：

当α＝β＝δ0＝0，（12）式退化为Jaky公式：K0＝1－sinφ′。

当R＝－1和3时，（9）和（10）式分别成为物部—冈部主动及被动土压力计算公式：

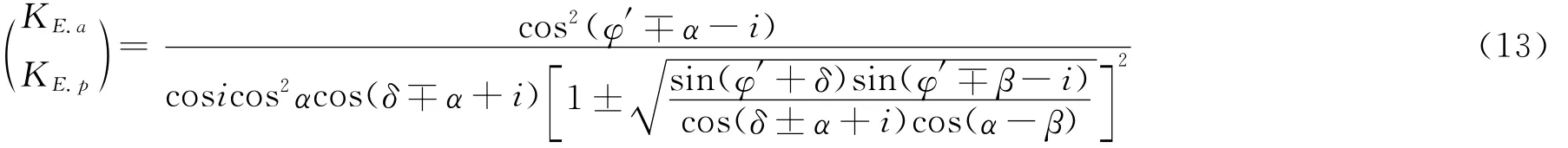
式（11）当i＝0时进一步退化为库仑主动及被动土压力计算公式：

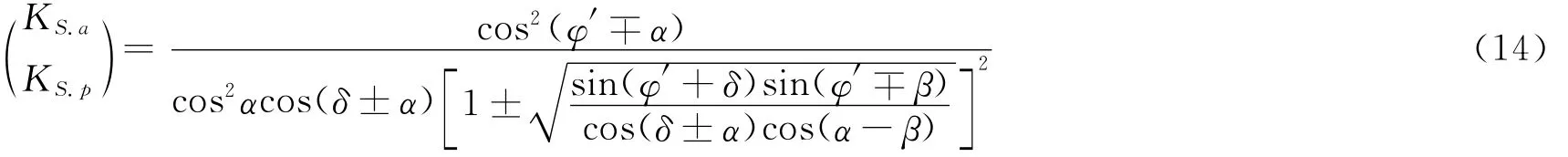
当R＝1时，由（9）式可知K＝1，即当墙后填土处于等向压缩状态时，对于各向同性填料而言，当侧向变形等于轴向变形时，其侧向应力与轴向应力的比值是1。

如果用起动摩擦角来表示，主动侧土压力系数的计算公式还可以写成

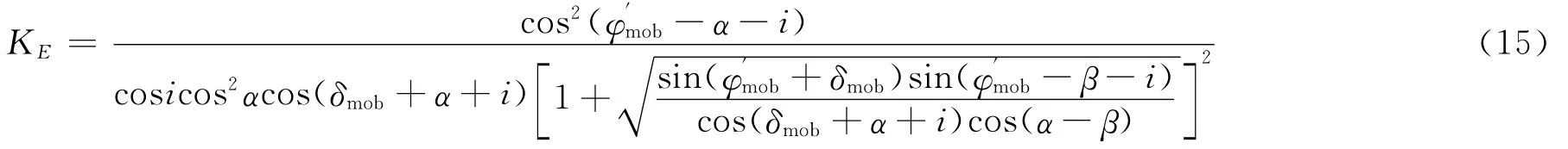
式（15）与式（9）是等价的。

如前所述，当墙背摩擦角较大以及挡墙位移量较大时，平面滑动面会高估被动侧土压力的大小，此时计算分析中采用曲面滑动面较为合适。基于对图9所示的曲面中间滑楔体OABC的受力分析，可以给出被动侧的土压力计算方法。滑动面AC上发挥的土的内摩擦角φ′mob由（4）式确定。如图9所示，在地震荷载作用下，滑动楔体除受到重力W和填土表面的均布荷载q以外，还受到竖直向上的惯性力kvW和水平向右的惯性力khW，填土表面还受到竖直向上的惯性力kvq和水平向右的惯性力khq。

根据力矩平衡条件，滑动土楔OABD所受的所有外力对对数螺旋线的极点E（xR，zR）的力矩为零，可分别求得填土自重和超载产生的土压力PpγE和PpqE，改变对数螺旋线的极点（xR，zR）的位置，分别求得PpγE和PpqE的极小值，即所求的土压力。限于篇幅，具体的数学公式推导过程在此不详细给出，可参考文献［37，41，42］。由土重和填土面堆载引起的土压力系数的计算公式分别如下：

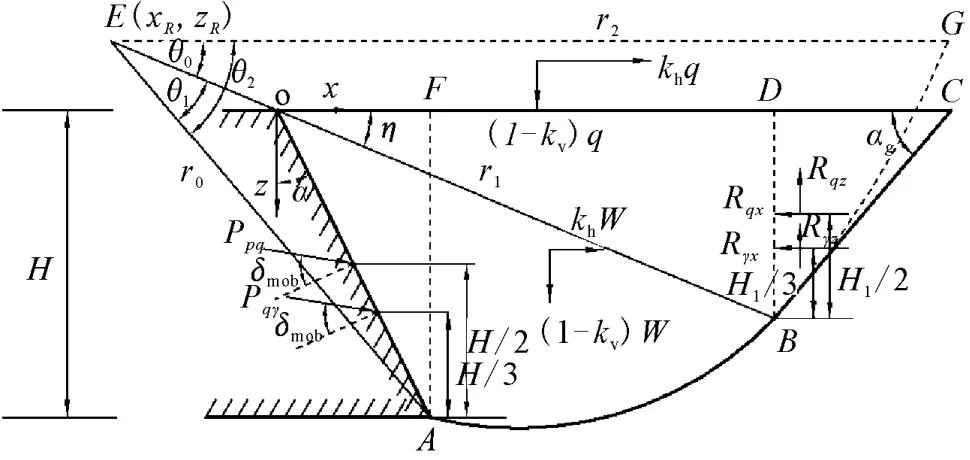
图9 曲面中间滑楔体受力分析图Fig．9 Mechanical analysis of curved intermediate soil wedge．

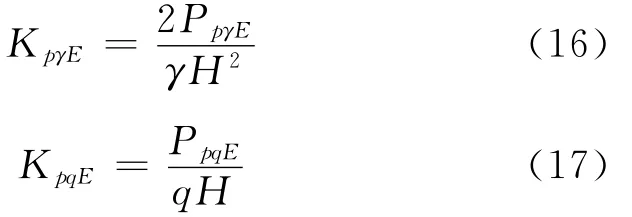
图10给出了被动侧土压力系数K随土的内摩擦角φ′、水平地震系数kh、墙背摩擦角δ和应变约束参数R的变化，计算中墙背倾角α，填土面倾角β和铅直地震系数kv均为零。从图中可以看出，R＝0时的土压力即为中性状态下的土压力，中性状态下的土压力系数随着水平地震系数的增大而增大，随着土的内摩擦角的增大而减小；而被动侧土压力系数随着水平地震系数的增大而减小，随着土的内摩擦角的增大而增大，随着墙背摩擦角的增大而增大。

以上计算方法可以被推广到计算浅埋式地下构筑物上作用的地震土压力，详见文献［43－45］。当墙后填土为超固结土和密砂时，剪切过程中随着剪切变形的增大填土强度会从峰值强度降低到残余强度。此时，抗剪强度指标的选取对于土压力计算至关重要，有关超固结土和密砂的主动和被动土压力计算方法作者也曾做过研究，相关研究成果详见文献［46，47］。当考虑墙后填土各向异性的性质时，作者也曾进行试验及理论研究，相关研究成果详见文献［37，48－51］。转动模式下的土压力计算方法详见文献［52，53］。当墙后填土位于地下水位以下时，地震荷载作用下的动土压力和水压力的计算方法详见文献［54－56］。

本文中的应变约束参数R是表征填土的侧向应变约束条件的重要参数。对大部分建筑物基础边墙的情形，数值分析表明R值大约为±1／8～1／4。基于对 Fang等［57，30－31］土压力模型试验结果的计算分析研究，给出应变约束参数 与挡墙位移量 的关系如下［28，47］：

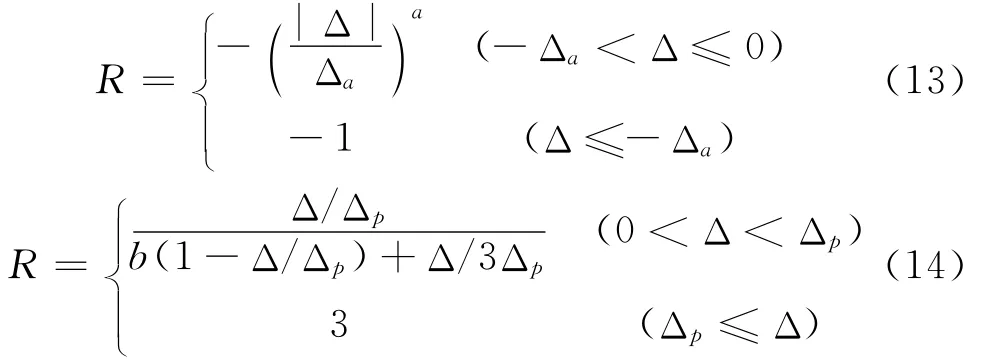
以上两式中a和p可由试验确定，a的取值范围是0．1～1，一般取为0．5；b取值范围一般约为0．015～0．03，一般取为0．025，砂土越密，b值越小。Δa、Δp和 Δr的 取 值 可 参 考 Terzaghi［29］、Matsuo 等［58］、Fang等［30－31，57］的土压力模型试验。

张建民等［28］基于对土压力模型试验结果的分析给出了墙背与填土之间的墙背摩擦角发挥值δmob随应变增量比Rε的变化的关系如下［28］：

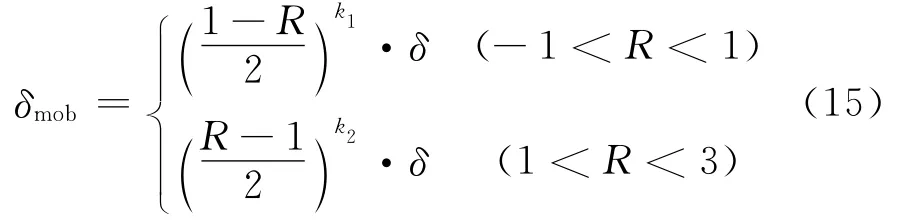
上式中k1和k2是由试验确定的常数，若假定δmob随R线性变化，则可取k1＝k2＝1，δ为墙背摩擦角。

4 计算方法的试验验证

图11给出了（8）～（10）式的计算结果与Fang等［57］的模型试验结果［57］的对比。计算中的参数为模型试验的实测数据：γactual＝15．4kN／m3；γinitial＝15．2kN／m3；φ′＝34°；δ＝17°；Δa＝0．51mm；a＝0．5。挡墙为平动的位移模式。从图9可以看出计算结果与试验结果基本吻合，验证了计算方法的有效性。

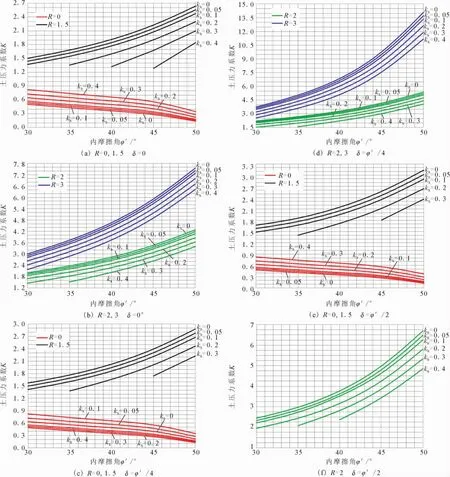
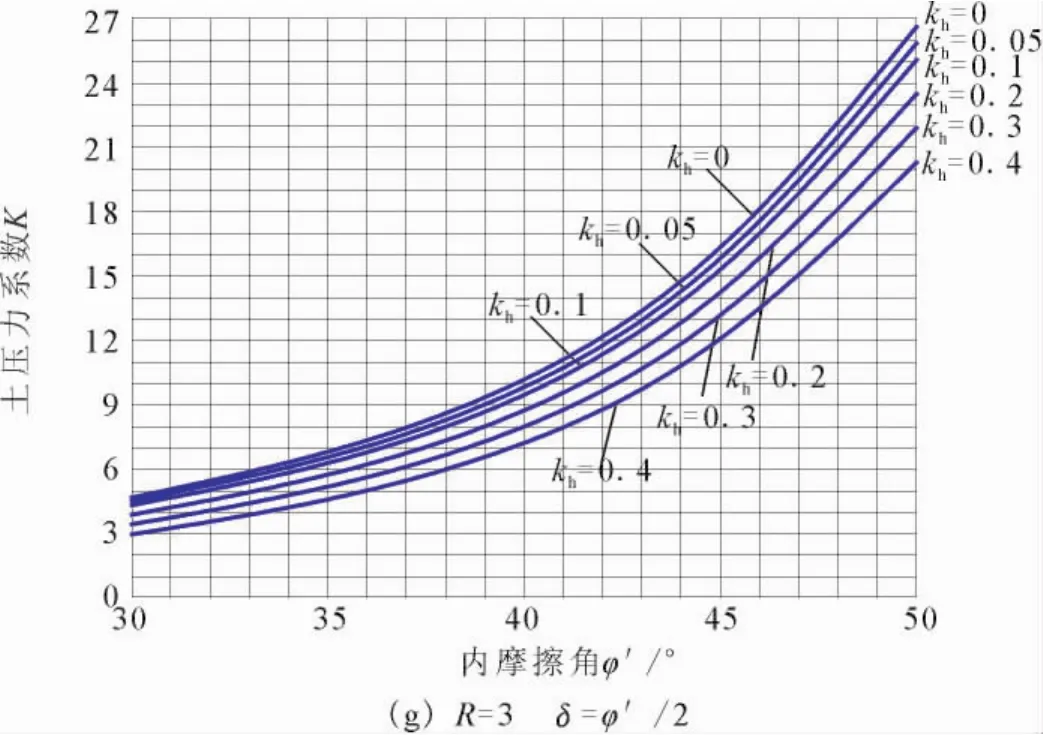
图10 土压力系数随内摩擦角、墙背摩擦角、水平地震系数和侧向应变约束参数的变化图表Fig．10 A chart showing the variation of earth pressure coefficient with internal friction angle，wall friction angle，horizontal earthquake coefficient and lateral strain parameter．

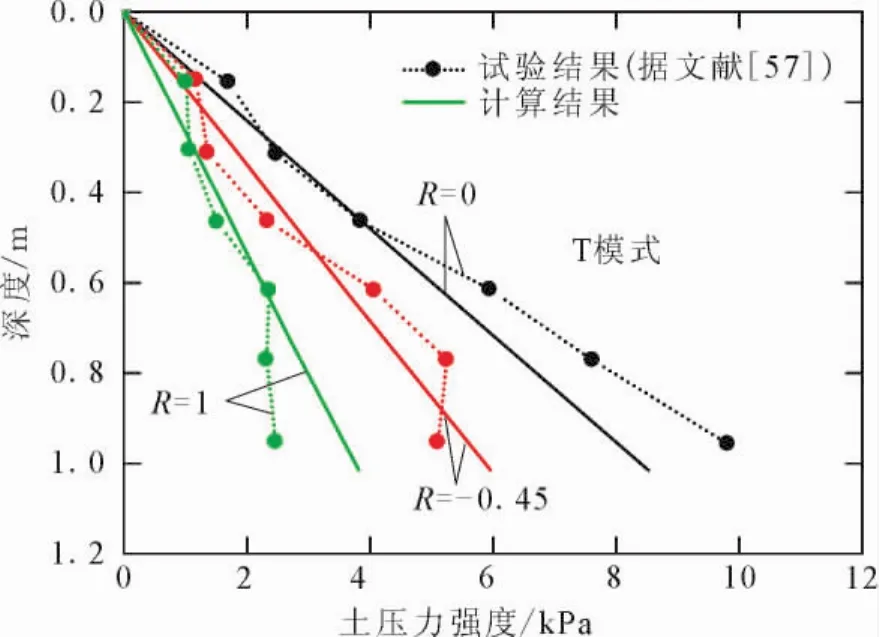
图11 主动侧土压力计算方法的试验验证Fig．11 Calidation of the method for computing earth pressure at the active side．

图12给出了本文的被动侧土压力计算方法的计算结果与Fang［30］的模型试验结果的对比。计算参数为Fang给出的试验参数：γ＝15．5kN／m3；φ′＝30．9°；δ＝19．2°；Δp＝0．18H。表征应变约束参数R随挡墙位移变化的参数b取为0．025。从图中可知计算结果与试验结果基本一致，验证了计算方法的有效性。

5 结语

简述了作者提出的考虑填土侧向变形的地震土压力计算方法，有以下几点主要结论及认识：

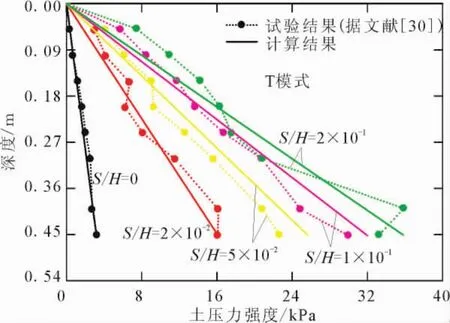
图12 被动侧土压力计算方法的试验验证Fig．12 Validation of the method for computing earth pressure at the passive side

（1）阐明压剪耦合效应的不同是土压力随应变约束条件变化的原因。随着挡墙位移量的变化，墙后填土处于不同的侧向应变约束条件下，其压缩效应和剪切效应相互影响的程度不同，亦决定了土所发挥出的剪切强度不同，这是土压力随挡墙位移量变化的物理本质。

（2）压剪耦合效应可以通过描述不同应变约束条件下的渐近状态来表述。不同的渐近状态实质上就是不同应变约束条件下填土经过沉积或压密达到稳定状态时的不同应力比，可理解为不同应变约束条件下的土压力系数。对内摩擦角一定的正常固结土，其土压力系数与应变增量比之间具有唯一性关系。提出的渐近状态准则能够描述填土发挥的摩擦强度与应变约束条件之间的定量关系。

（4）基于渐近状态准则及中间滑楔体概念，给出了可考虑填土侧向变形影响、可计算从主动到被动状态之间的任意中间状态下的地震土压力公式，建议了针对应变局部化等常见实用条件的计算方法。

（5）通过Fang等的试验研究成果对本文提出的地震土压力计算公式及算法进行了验证分析，初步表明其有效性和合理性。

［1］ Mononobe N，Matsuo H．On the determination of earth pressure during earthquakes［A］∥Proceedings of the 6th World Engineering Congress［C］．Tokyo：［s．n．］，Japan，1929，（9）：177－185．

［2］ Okabe S．General theory on earth pressure and seismic stability of retaining walls and dams［J］．Journal of the Japanese Society of Civil Engineering，1924，10（6）：1277－1323．

［3］ Morrison E E，Ebeling R M．Limit equilibrium computation of dynamic passive earth pressure［J］．Canadian Geotechnical Journal，1995，32：481－487．

［4］ Kumar J．Seismic passive earth pressure coefficients for sands［J］．Canadian Geotechnical Journal，2001，38（4）：876－881．

［5］ Subba Rao K S ，Choudhury D S．Seismic passive earth pressures in soils［J］．Journal of Geotechnical and Geoenvironmental Engineering，2005，131（1）：131－135．

［6］ Kumar J，Chitikela．Seismic passive earth pressure coefficients using the method of characteristics［J］．Canadian Geotechnical Journal，2002，39：463－471．

［7］ Cheng Y M．Seismic lateral earth pressure coefficients for c－Φ soils by slip line method［J］．Computers and Geotechnics，2003，30：661－670．

［8］ Prakash S，Saran S．Static and dynamic earth pressures behind retaining walls［A］∥Proceedings of the 3rd Symposium on Earthquake Engineering［C］．Roorkee，India：University of Roorkee，1966，277－288．

［9］ Prakash S，Basavanna B M．Earth pressure distribution behind retaining walls during earthquake［A］∥Proceedings of the 4th World Conference on Earthquake Engineering［C］．Santiago：［s．n．］，Chile，1969，133－148．

［10］ Das B M，Puri V K．Static and dynamic active earth pressure［J］．Geotechnical and Geological Engineering，1996，14：353～366．

［11］ Chen W F．Limit analysis and soil plasticity．Developments in geotechnical engineering［M］．Amsterdam，The Netherlands：Elsevier，1975．

［12］ Chen W F，Liu X L．Limit analysis in soil mechanics［M］．Developments in geotechnical engineering，52［G］．Amsterdam，The Netherlands，Elsevier：1990：477．

［13］ Soubra A H．Static and seismic passive earth pressure coefficients on rigid retaining structures［J］．Canadian Geotechnical Journal，2000，37（2）：463－478．

［14］ Matsuo H．Experimental study on the distribution of earth pressure acting on a vertical wall during earthquakes［J］．Journal of the Japan Society of Civil Engineers，1941，27（2）：211－230．

［15］ Matsuo H，Ohara S．Lateral earth pressure and stability of quay walls during earthquakes［A］∥Proceedings of 2nd World Conference on Earthquake Engineering［C］．Tokyo：［s．n．］，Japan，1960，1：165－183．

［16］ Ishii Y．，Arai H，Tsuchida H．Lateral earth pressure in an earthquake［A］∥Proceedings of the 2nd World Conference on Earthquake Engineering［C］．Tokyo：［s．n．］，Japan，1960，1：211－230．

［17］ Ichihara M，Matsuzawa H．Earth pressure during earthquake［J］．Soils and Foundations，1973，13（4）：75－86．

［18］ Sherif M，Ishibashi I，Lee C D．Earth pressures against rigid retaining walls［J］．Journal of geotechnical engineering，ASCE，1982，108（GT5）：679－695．

［19］ Sherif M A，Fang Y S．Dynamic earth pressures on walls rotating about the top［J］．Soils and foundations，1984，24（4）：109－117．

［20］ Ishibashi I，Fang Y S．Dynamic earth pressures with different wall movement modes［J］．Soils and Foundations，1987，27（4），11－22．

［21］ Seed H B，Whitman R V．Design of earth retaining structures for dynamic loads［A］∥Proc．ASCE Specialty Conference on lateral stresses in the ground and design of earth retaining structures［C］．［S．l］：Cornell University ，USA，1970，103－147．

［22］ Shakya D A．Engineering solutions for the displacement of rigid retaining walls subjected to earthquake loads［D］．［S．l］：University of Missouri－Rolla，USA，1987：1－115．

［23］ Prakash S，Wu Y，Rafnsson E A．On Seismic design displacements of rigid retaining walls［A］∥Proceedings of the 3rd International Conference on Recent Advances in Geotechnical Engineering and Soil Dynamics［C］．St．Louis，MO，III：［s．n．］：1183－1192

［24］ Iai S．Rigid and flexible retaining walls during Kobe earthquake［A］∥Proceedings of the 4th International Conference on Case Histories in Geotechnical Engineering，St．Louis，MO．，March 8－12，CD－ROM，SOA－4，108－127．

［25］ Wu Y．Displacement－based analysis and design of rigid retaining walls during earthquakes［D］．USA：University of Missouri－Rolla，1999：1－223．

［26］ Psarropoulosa P N，Klonarisb G，Gazetasa G．Seismic earth pressures on rigid and flexible retaining walls［J］．Soil Dynamics and Earthquake Engineering，2005，25，795－809．

［27］ Maleki S，Mahjoubi S．A New Approach for estimating the seismic soil pressure on retaining walls［J］．Transaction A：Civil Engineering，2010，17（4）：273－284．

［28］ Zhang J M，Shamoto Y，Tokimatsu K．Evaluation of earth pressure under any lateral deformation［J］．Soils and Foundations，1998，38（1）：15－33．

［29］ Terzaghi K．Large retaining wall tests［J］．Engineering News Record，1934，112：136–140．

［30］ Fang Y S，Chen T J，Wu B F．Passive earth pressures with various wall movements［J］．Journal of Geotechnical Engineering，1994，120（8）：1 307–1 323．

［31］ Fnaf Y S，Ho Y C，Chen T J．Passive earth pressure with critical state concept［J］．Journal of Geotechnical and Geoenvironmental Engineering，2002，127（3）：248－257．

［32］ Zhang J M，Shamoto Y，Tokimatsu K．Seismic earth pressure theory for retaining walls under any lateral displacement［J］．Soils and Foundations，1998，38（2）：143－163．

［33］ Zhang J M．Cyclic Critical Stress State Theory of Sand with Its Application to Geotechnical Problems［R］．Research Report of Tokyo Institute of Technology，Tokyo，1997：78－100．

［34］ Gudehus G，Goldscheoder M，Winter H．Mechanical properties of sand and clay and numerical integration methods：some sources of errors and bounds of accuracy［A］∥G udehus．Finite elements in geomechanics［C］．Balkema，Rotterdam，1977，121－150．

［35］ Chu J，Lo S－C R．Asymptotic behavior of a granular soil in strain path testing［J］．Geotechnique，1994，44（1）：65–82．

［36］ Asaka Y，Tokimatsu K，Iwasaki K，et al．A simple stressstrain relation based on stress－path behavior in strain－path controlled triaxial tests ［J］．Soils and foundations，2003，43（2）：55－68．

［37］ 宋飞．考虑侧向变形的各向异性填土土压力计算方法及试验研究［D］．北京：清华大学，2009：152－165．

Song Fei．Evaluation and experimental study of earth pressure for anisotropic sand under any lateral deformation［D］．Beijing：Tsinghua University，2009：152－165．

［38］ 张建民，宋飞．砂土的压剪效应与渐近状态准则［J］．岩土工程学报，2008，30（2）：166–171．

Zhang Jian－Min，Song Fei．Compression－dilatancy coupling effect and asymptotic state criterion of sand ［J］．Chinese Journal of Geotechnical Engineering，2008，30（2）：166–171．

［39］ Terzaghi K．Theoretical Soil Mechanics［M］．Wiley，New York．1943．

［40］ Sherif M A，Fang Y S，Sherif R I．KaandK0behind rotating and non－yielding walls［J］．Journal of Geotechnical Engineering，ASCE，1984，110（1）：41－56．

［41］ 宋飞，张建民．平动模式下刚性挡墙被动侧土压力计算方法［A］∥中国土木工程学会第十届土力学及岩土工程学术会议论文集（下册）［C］．重庆：［s．n．］，2007：447－451．

Song Fei，Zhang Jian－Min．Earth pressure at the passive side against rigid retaining wall under translational mode［A］∥Proceedings of the 10th Chinese National Conference on Soil Mechanics and Geotechnical Engineering［C］．Chongqi：［s．n．］，2007：447－451．

［42］ Song F，Zhang J M．Evaluation of Seismic Earth Pressures at the Passive Side［A］∥Proceedings of the 14th World Conference on Earthquake Engineering［G］．Beijing，：［s．n．］，2008，CD：14－04－02－0122．

［43］ Zhang J M，Shamoto Y，Tokimatsu K．Seismic earth pressure against basement wall［A］∥Proceedings of the 8th International Conference on Soil Dynamics and Earthquake Engineering［C］．Istanbul，Turkey：1997．

［44］ Zhang J M，Shamoto Y，Tokimatsu K．Earth pressures on rigid walls during earthquakes［J］．ASCE Geotechnical Special Publication，1998，75（2）：1053－1070．

［45］ Zhang G，Zhang J M．Simplified Methods for dynamic soil and semi－berried structure interaction［A］∥Proceedings of 4th International Conference on Advances in Geotechnical Earthquake Engineering and Soil Dynamics［C］．［S．l．］：San Diego，CA，USA，2001：345－350．

［46］ Zhang J M，Song F，Li D．Effect of strain localization on seismic active earth pressures ［J］．Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2010，136（7）：999－1003．

［47］ 宋飞，张建民．考虑挡墙位移效应的被动侧土压力计算方法［J］．岩土力学，2011．32（1）：151－157．

Song Fei，Zhang Jian－min．Evaluation of earth pressure at the passive side considering wall displacement effect［J］．Rock and Soil Mechanics 2011．32（1）：151－157．

［48］ 宋飞，张建民．考虑侧向变形的各向异性砂土土压力试验研究［J］．岩石力学与工程学报，2009，28（9）：1884－1895．

Song Fei，Zhang Jian－Min．Investigation of earth pressure for anisotropic sand considering wall movement［J］．Chinese Journal of Rock Mechanics and Engineering，2009，28（9）：1884－1895．

［49］ 宋飞，张建民．各向异性砂土渐近状态试验研究［J］．岩土工程学报，2010，32（4）：551－561．

Song Fei，Zhang Jian－min．Experimental study of asymptotic behavior of anisotropic sand［J］．Chinese Journal of Geotechnical Engineering，2010，32（4）：551－561．

［50］ 宋飞，张建民，刘超．各向异性砂土K0试验研究［J］．岩土力学，2010，31（12）：3727－3732．

Song Fei，Zhang Jian－Min，LIU Chao．Experimental study of K0for anisotropic sand［J］．Rock and Soil Mechanics，2010，31（12）：3727－3732．

［51］ 宋飞，张建民．各向异性砂土主动侧土压力计算方法［J］．岩土力学，2011，32（4）：1029－1034．

Song Fei，Zhang Jian－Min．Evaluation of earth pressure at the active side for anisotropic sand［J］．Rock and Soil Mechanics，2011，32（4）：1029－1034．

［52］ Song F，Zhang J M．Zhang L Y．Evaluation of earth pressures against rigid retaining structures with RTT mode ［J］．Advanced Materials Research，2011，168：200－205．

［53］ Song F，Zhang J M．Estimation of seismic earth pressures against rigid retaining structures with rotation mode［J］．The Open Civil Engineering Journal，2011，5：52－58．

［54］ Zhang J M，Shamoto Y．Total stress change during cyclic loading underK0conditions［A］∥Proceedings of the 3rd International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics［C］．Missouri：［s．n．］，USA，1995：1，18．

［55］ Zhang J M，Shamoto Y，Tokimatsu K．Total lateral stress change in saturated sand after liquefaction under different strain constraints［A］∥Proceedings of the 11th World Conference on Earthquake Engineering［C］．Mexico，1996：1053．

［56］ Zhang J M，Shamoto Y，Sato M．Dynamic soil and water pressures against quay walls［A］∥Proceedings，98’IS Centrifuge［C］．Tokyo：［s．n．］，1998，154－159．

［57］ Fang Y S，Ishibashi I．Static earth pressures with various wall movements［J］．Journal of Geotechnical Engineering，1986，112（3）：317–333．

［58］ Matsuo M，Kenmochi S，Yagi H．Experimental study on earth pressure of retaining wall by field tests［J］．Soils and Foundations，1978，18（3）：27－41．