罕遇地震下空心薄壁高墩大跨T形刚构桥弹塑性地震反应分析①

李 林

（兰州铁道设计院有限公司，甘肃 兰州 730000）

0 引言

受地形条件控制，铁路桥梁在跨越高山峡谷时往往需要采用高墩大跨结构。由于T形刚构桥具有跨越能力大、结构受力合理、墩梁固结无需巨型支座、整体刚度大且施工方便等特点，近年来在我国西北黄土高原地区得到广泛应用。为满足铁路桥梁的刚度要求和经济性要求，高于30m的桥墩一般均采用薄壁空心截面形式的钢筋混凝土桥墩。5·12汶川大地震后，高烈度地震区大跨度桥梁的抗震设计得到充分重视。我国最新修订版的《铁路工程抗震设计规范》（GB50111－2006）［1］在设防理念上采用了分级设防的思想，即根据地震动概率水准的不同制定不同的设防目标，具体而言就是“小震不坏、中震可修、大震不倒”的三水准抗震设计要求。规范中明确规定：对于重要桥梁，在罕遇地震作用下应按非线性时程反应分析法［2］对钢筋混凝土桥墩进行延性验算或最大位移分析。但铁路规范中对于弹塑性分析方法中的计算模型及相关参数选取则没有具体的规定及缺乏指导。在罕遇地震下薄壁空心高墩大跨T构铁路桥的抗震性能是否满足“大震不倒”的要求需要得到确认，因此深入研究此类桥梁在罕遇地震下的抗震性能十分必要。

目前国内对于采用薄壁空心高墩大跨T构铁路桥关于延性抗震方面的研究文献较少。对于同类桥梁，《欧洲桥梁抗震设计规范》建议设计成有限延性或基本弹性；文献［3］对国内外桥梁延性抗震构造设计方面作了比较；文献［4］采用Pushover分析方法计算结构位移延性能力；文献［5］用设置多个塑性铰的分析模型研究连续刚构桥的弹塑性地震反应。

T形刚构桥由于在墩顶与梁底处采用固结，在罕遇地震作用下可能在墩顶与墩底均形成塑性铰，进入弹塑性受力状态，因此需要计入非线性塑性变形的耗能影响对结构进行抗震分析并做延性设计，以达到抗震性能要求Ⅲ的设防目标。鉴于弹塑性地震响应分析的复杂性，本文以一座（96＋96）m空心薄壁高墩大跨T形刚构铁路桥为工程背景实例，在前人研究成果的基础上，使用有限元软件，利用PM集中塑性铰单元及Takeda武田三线型滞回模型进行罕遇地震作用下非线性动态时程弹塑性地震反应分析，并进行相应的抗震性能评价，旨在对同类铁路桥梁结构的延性抗震具体计算分析方法提供参考和借鉴作用。

1 工程背景

某一在建特大桥工程位于宁夏固原市原州区东北部一条单线地方铁路上，横跨一深切冲沟，沟槽深约76m。主桥采用96＋96m预应力混凝土T形刚构桥。桥址位于Ⅷ度地震区，动峰值加速度Ag＝0．30g，场地土特征周期Tg＝0．4s，属于II类场地。主桥立面图见图1。

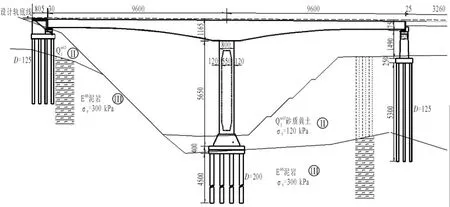
图1 主桥立面布置图（单位：cm）Fig．1 The elevation layout of main bridge（unit：cm ）．

上部结构主梁为变截面预应力混凝土箱梁，单箱单室结构。顶板宽7．5m，底宽5．0m，主墩支点截面处梁高11．0m，跨中截面梁高4．5m，顶板厚0．46m，主墩支点截面处底板厚1．3m，跨中截面底板厚0．5m，梁高和底板厚度自根部至两端均呈1．8次抛物线变化，墩顶箱梁设置2．0m横隔板2道，梁端设置2．5m厚的横隔板1道。采用纵、横、竖三向预应力体系。主桥桥墩采用变截面矩形薄壁墩，4×6根Φ2m的钻孔灌注桩基础。墩高50m，墩身顺桥向厚度8．0m，壁厚1．2m，内外壁为直坡变化；墩顶横桥向宽度7．5m，壁厚为1．2m，墩身横桥外侧按40：1、内侧按60：1的坡度变化，墩底横桥向宽度10．0m。主墩结构如图2所示。

2 计算方法及地震波的选取

2．1 计算方法

时程分析法［2］计算结构在每个时刻的地震反应（内力和变形）。用此法进行计算时，当输入地震波的作用较为强烈以至结构某些部位强度达到屈服进入塑性时，通过构件刚度的变化可求出弹塑性阶段的结构内力与变形。这时结构薄弱层间位移可能达到最大值，从而造成结构的破坏直至倒塌。由于非线性分析的复杂性，计算分析时按如下假定：（1）上部结构为弹性，非线性行为只发生在下部桥墩中；（2）考虑“桩－土”作用，将地基土对结构的约束用弹簧来模拟，其刚度按m法计算；（3）桥墩进入非线性工作状态的部位按照弹性状态下初步计算的内力值分析确定。

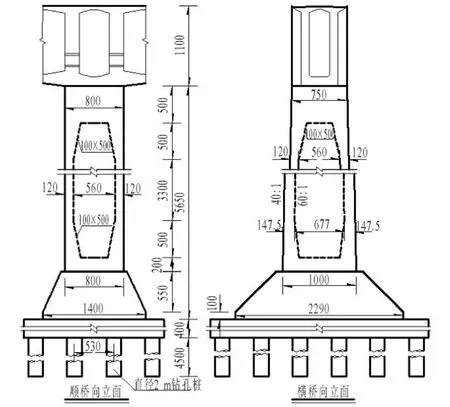
图2 桥墩结构立面图（单位：cm）Fig．2 The elevation layout of pier structure（unit：cm ）．

为真实的模拟桥梁结构的力学特性，利用大型结构分析软件Midas／Civil建立空间梁单元计算模型，采用分段线性逐步积分法对该桥进行弹塑性地震反应分析。恢复力滞回模型采用常用的Takeda武田三线型模型。由于桥墩空心部分更容易进入塑性状态，因此在T构墩顶部和底部空心部分均设置塑性铰［5］。塑性铰的长度取截面计算方向的尺寸，塑性铰区单元用弹塑性梁单元来模拟，铰类型采用能够考虑轴力对铰的弯曲屈服强度影响的P－M集中铰。按照铁路震规要求，在全桥罕遇地震分析过程中，在顺桥向和横桥向分别输入地震波，不考虑竖向地震作用，同时不考虑活载组合，仅考虑恒载效应。结构离散计算模型见图3。

2．2 地震波的选取

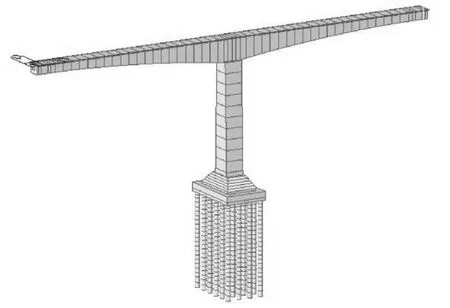
图3 计算模型Fig．3 Analysis model．

输入地震波的特性对时程分析结果有很大的影响，选择的原则是使输入地震波的特性和建筑场地的条件相符合［6］。地震波的峰值应反映桥址所在地区的烈度，而其频谱组成应反映场地的卓越周期和动力特性。震规要求在对特殊结构进行时程分析时应选择多条地震波进行分析比较。由于该桥没有提供安评地震波，本文选择了两条国内外常用的强震记录：El－centro波和Taft波。在输入地震波加速度时，将各记录的峰值进行了调整，使输入的水平加速度峰值达到罕遇地震作用下对应Ⅷ度区的0．57 g，如图4所示。

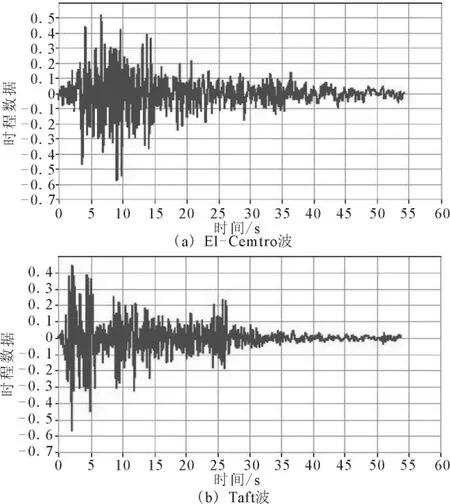
图4 输入的罕遇地震波Fig．4 The input waves of high－level earthquake．

3 弹塑性时程反应计算及结果分析

3．1 桥墩截面弯矩－曲率分析

在结构的弹塑性分析中，墩柱截面的非线性特性使用截面的弯矩－曲率关系曲线（Moment Curvature Curve）来描述。利用截面尺寸和实配钢筋获得截面的M－Φ曲线，同时使用该曲线可评价钢筋混凝土截面的抗震性能。通过定义截面尺寸，选择相应的材料本构模型，并输入混凝土和钢筋的性质及截面的轴向力，程序计算出截面的一些关键特性，例如屈服特性值、极限特性值等。对薄壁空心桥墩墩顶及墩底塑性铰截面进行截面顺桥向弯矩－曲率分析计算的结果见表1。

表1 截面弯矩－曲率关系

3．2 计算结果及分析

限于篇幅，文中只对加速度峰值为0．57g的两条罕遇地震波在顺桥向的地震反应进行弹塑性非线性时程分析，分别计算出两条波作用下的墩顶位移、墩顶截面及墩底截面的内力及塑性铰区域弯矩－曲率滞回曲线。为便于对比，同时又分别按照反应谱法［2］和线性动态时程法对结构进行了计算，计算结果见图5～图7及表2所示。

表2 罕遇地震下顺桥向地震反应（α＝0．57g）

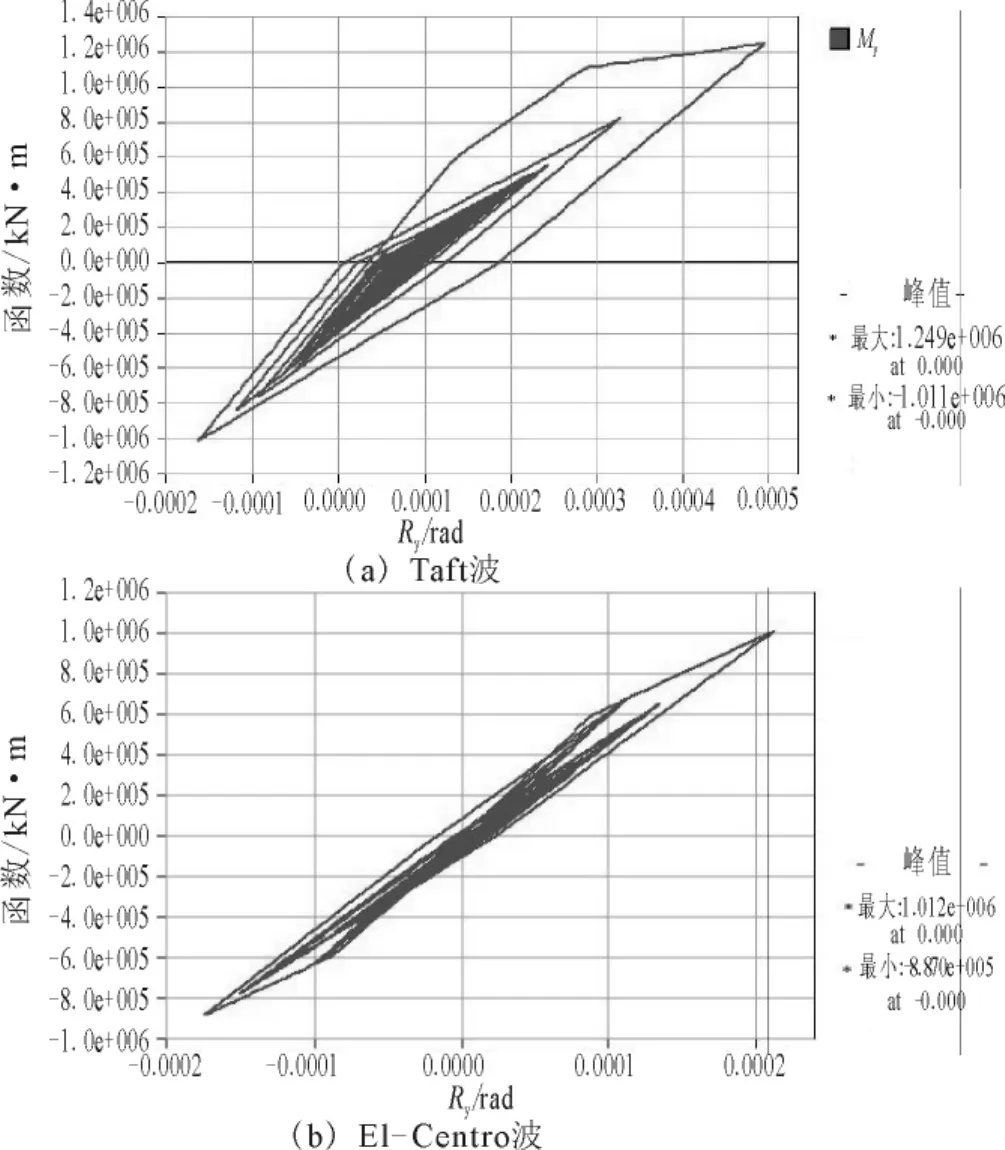
图5 顺桥向墩底弯矩－曲率滞回曲线Fig．5 Moment－curvature hysteretic curves at pier base along the bridge direction．

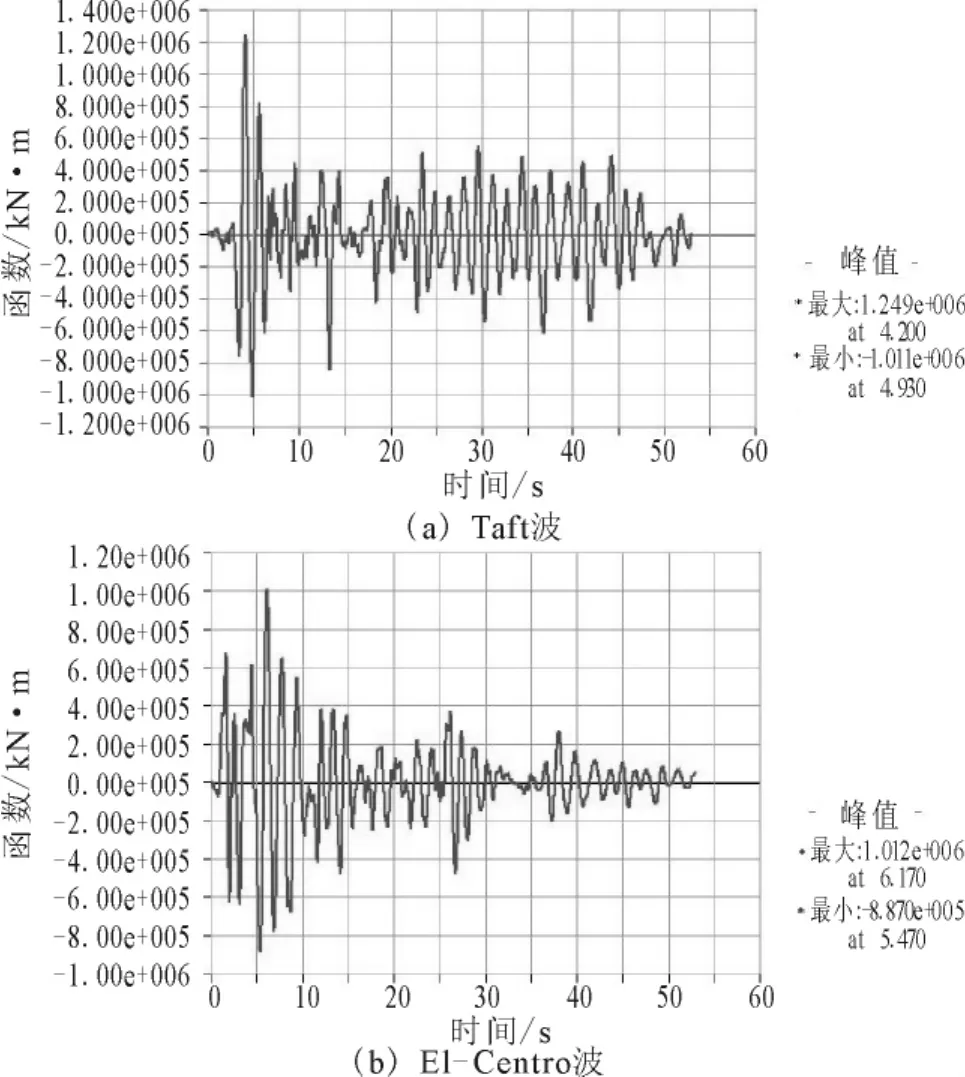
图6 顺桥向墩底弯矩反应时程Fig．6 The time history of moments at pier base along the bridge direction．

从表2的计算结果对比可看出，与线性时程分析和反应谱分析的计算结果相比，考虑弹塑性的非线性时程地震反应内力明显减小，尤其是墩顶截面弯矩减小幅度最大，非线性时程计算的墩顶截面弯矩只有线性时程计算的1／3～1／2。

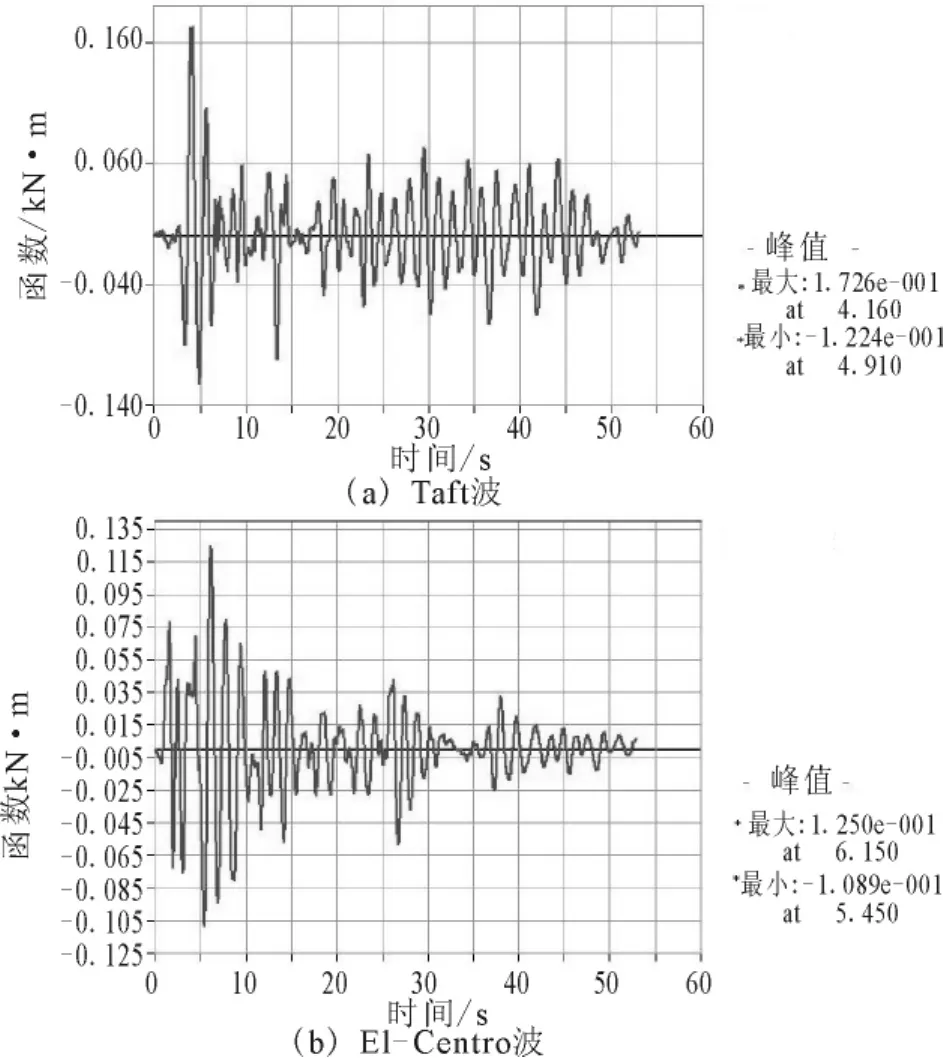
图7 顺桥向墩顶位移反应时程Fig．7 The time history of displacements at pier top along the bridge direction．

墩顶截面在El－Centro波和Taft波作用下，塑性铰区均处于线弹性工作状态，截面尚未进入开裂阶段，离到达屈服阶段尚远，结构不会有损伤。

从墩底截面塑性铰弯矩－曲率滞回曲线可以明显看出，在El－Centro波作用下墩底截面已经进入开裂阶段末段，但尚未进入屈服阶段；在Taft波作用下墩底截面塑性铰则已经进入塑性工作状态，截面进入屈服阶段但塑性反应幅度不大，结构损伤较小，远未达到极限破坏状态。Taft波引起的地震反应比El－Centro波相对要大。

3．3 位移反应验算

根据截面弯矩－曲率关系表中墩底屈服弯矩为1．091E＋06kN·m，反算出对应墩顶顺桥向的屈服位移为0．127m。El－Centro波作用下的非线性位移延性比μu＝0．125／0．127＝0．984；Taft波作用下的非线性位移延性比μu＝0．173／0．127＝1．362，均满足规范“非线性位移延性比μu＜4．8”的要求。

由于文献［1］附录F．0．1－1提供了根据线性弯矩比来计算非线性位移延性比的简化方法，这里也按照简化方法作一验证：

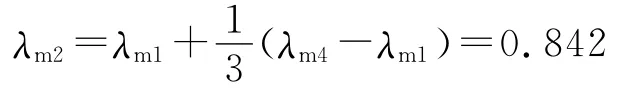
由此可以计算得到表3中桥墩非线性位移延性系数。

表3 非线性位移延性比

由上表可以看出文献［1］提供的根据线性弯矩比来计算非线性位移延性比的简化方法得出的结果与采用非线性时程计算的结果比较接近，说明采用简化计算方法还是相对适用的。

4 结论

采用空心薄壁高墩T形刚构铁路桥在加速度峰值为0．57g的顺桥向两条罕遇地震波作用下，墩底截面塑性铰区处于较弱的非线性受力状态，其受到的损伤较小，具有较好的抗震能力。结构考虑非线性塑性反应后的地震力与弹性相比明显减小，其中Taft波引起的地震反应比El－Centro波相对要大。墩顶截面均处于未开裂的线弹性工作阶段，结构不会有损伤；墩底截面在El－Centro波作用下进入开裂阶段末段，未到达屈服阶段，但在Taft波作用下进入较弱的屈服塑性工作阶段，结构损伤较小，桥墩无破坏现象发生，满足规范“大震不倒”的要求。且在罕遇地震作用下，墩顶位移较小，非线性位移延性比最大仅为1．362，延性验算满足规范要求，在罕遇地震下结构处于有限的非线性塑性状态，这也充分说明了空心薄壁铁路高墩的延性抗震能力是有足够保障的。

［1］ GB50111－2006．铁路工程抗震设计规范［S］．北京：中国计划出版社，2006．GB50111－2006．Railway engineering anti－earthquake design specification［S］．Beijing：China Plans to Press，2006．

［2］ 吴小峰，孙启国，狄杰建，等．抗震分析反应谱法和时程分析法数值仿真比较［J］．西北地震学报，2011，33（03）：275－278．

WU Xiao－feng，SUN Qi－guo，DI Jie－jian．A Numerical Simulation Comparison between Response Spectrum Analysis and Time History Analysis［J］．Northwestern Seismological Journal，2011，33（03）：275－278．

［3］ 薜瑞杰，袁万城．国内外桥梁延性抗震构造设计比较［J］．工程抗震与加固改造，2009，31（02）：1－8．

XUE Rui－jie，Yuan Wan－cheng．Comparison on Domestic and Overseas Constructional Details for Ductility Seismic Design of Bridge［J］．Earthquake Resistant Engineering and Retrofitting，2009，31（02）：1－8．

［4］ 梁智垚．桥梁高墩位移延性能力计算方法研究［J］．工程抗震与加固改造，2005，27（05）：57－62．

LIANG Zhi－yao．Study on Calculational Methods of Displacement Ductility Capacity of Tall Pier［J］．Earthquake Resistant Engineering and Retrofitting，2005，27（05）：57－62．

［5］ 夏修身，陈兴冲，王常峰，等．高墩大跨连续刚构桥抗震性能研究［J］．西北地震学报，2010，32（1）：88－90．

XIA Xiu－shen，CHEN Xing－chong，WANG Chang－feng，et al．Study on Seismic Performance of Tall－pier and Long－span Continuous Rigid－framed Bridge［J］．Northwestern Seismological Journal，2010，32（1）：88－90．

［6］ 胡文源，邹晋华．时程分析法中有关地震波选取的几个注意问题［J］．南方冶金学院学报，2003，24（4）：25－28．

HU Wen－yuan，ZOU Jin－hua．Time History Analysis Method for Seismic Wave Selection of A Few Pay Attention to the Problem［J］．Journal of Southern Institute of Metallurgy，2003，24（4）：25－28．