双向中继通信中的联合正交物理层网络编码

李 博，王 钢，杨洪娟，刘荣宽

(哈尔滨工业大学通信技术研究所，150001哈尔滨)

物理层网络编码(physical-layer network coding，PNC)［1－2］技术自从 2006 年被提出以来，受到无线通信领域学者的广泛关注.这是由于，在双向中继通信系统(two-way relay channels，TWRC)［3－4］中，PNC 方案比传统多跳方案和网络编码(network coding，NC)方案分别可以提高100%和50%的系统吞吐量［1］.但是，大部分有关于物理层网络编码的研究主要都集中于对称信道，即上行信道和下行信道具有相同的信噪比(signal-to-noise ratio，SNR).文献［5］研究了2个下行信道具有不同信噪比的情况，给出了相应的解决方法，文献［6］研究了两源节点采用不同调制方式的情况.但是，截止到目前，还没有对于PNC在以下2种非对称条件下的研究成果发表:1)上行信道与下行信道具有不同的信噪比;2)2个上行信道具有不同的信噪比.

文献［7］提出了一种新方案称为正交物理层网络编码(orthogonalphysical-layernetwork coding，OPNC)，OPNC方案在保证通信时隙数与PNC相等的同时，由于采用了正交载波，获得了一定的系统误比特率(bit error rate ratio，BER)增益.本文基于文献［7］正交载波思想，提出了一种新的联合正交方案，称为联合正交物理层网络编码(combined orthogonalphysical-layernetwork coding，COPNC).在信道对称的条件下，分析了各种方案的误比特率性能;在以上2种非对称条件下，仿真实验表明 COPNC方案与 PNC以及OPNC方案相比，可以获得更好的BER性能.

1 系统模型

本文研究如图1所示的双向中继通信系统模型.节点1与节点2之间没有直达链路，必须通过节点R中继来交换信息.假设所有节点都工作在半双工模式下，即每个节点不能同时进行信息的收发.在时隙1，节点1和2把各自的已调信息x1和x2同时发送到节点R，节点R对收到的混叠信号进行处理，得到综合的信息xR，并在时隙2将其广播到节点1和2，节点1和2在已有信息的辅助下解码出对方传送的信息.需要注意的是，在PNC和NC方案中，中继R对信息综合的过程采用XOR的方式.此处定义时隙1为上行阶段，定义时隙2为下行阶段.本文假设不采用信道编码或者采用端到端(end-to-end channel coding)的信道编码［8］，即中继节点不必考虑信道的编解码，节点1和2都采用二进制移相调制(binary phase shift keying，BPSK)调制，所有信道都为加性高斯白噪声(additive white Gaussian noise，AWGN)信道.

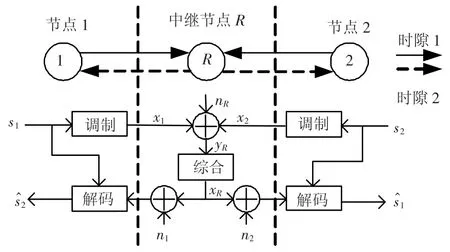
图1 双向中继通信系统模型

2 物理层网络编码方案与正交物理层网络编码方案

2.1 PNC方案

当系统采用PNC方案时，节点1和2在上行阶段把各自的已调信息乘以理想同步的载波.后发射到无线信道，中继节点R接收到叠加噪声的混叠信号后，对其进行如图2所示的信号处理过程.经过相关器后得到的基带信号为

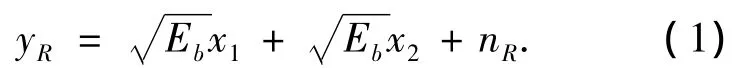
式中:nR是均值为0，功率N0/2的加性高斯白噪声.

经过判决与映射得到综合信息sR，然后对sR进行BPSK调制得到已调信息xR并在下行阶段进行广播.PNC方案对两路信号的综合处理表达式为

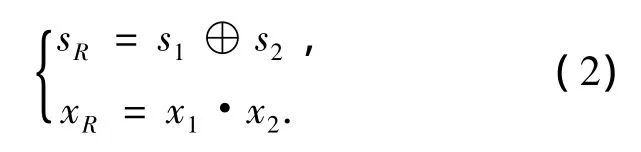
在下行阶段，节点1和2各自利用已有信息与节点R的广播信息解码出对方的信息.

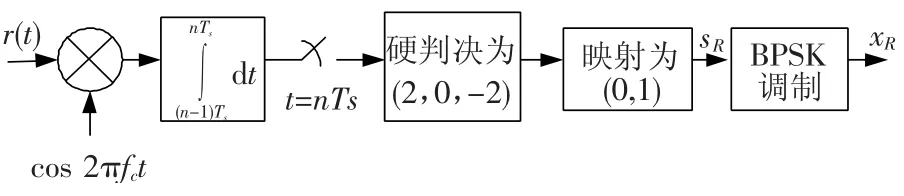
图2 PNC方案中继节点R的信号处理过程

文献［1］给出了当所有信道具有相同的信道条件，即所有信道完全对称的情况下，中继节点的判决门限以及映射方法.由判决门限可以计算出中继节点的判决错误概率为

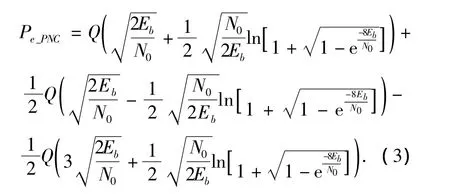
式中:Eb为每比特能量，函数Q(x)参见文献［11］.由于下行阶段就是点到点的BPSK调制传输，下行错误概率为)［11］.所以整个系统的误比特率为

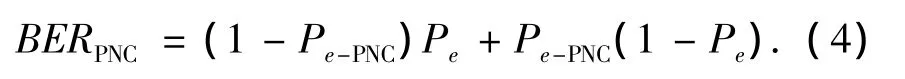
2.2 OPNC方案

OPNC方案与PNC方案的主要区别在于节点1和2在发送信息时的载波有π/2的相位差，即正交载波.不妨假设节点1的载波为cos 2πfct，节点2的载波为sin 2πfct.上行阶段节点R收到叠加噪声的混叠信号，处理过程如图3所示.节点R收到的基带信号表示为

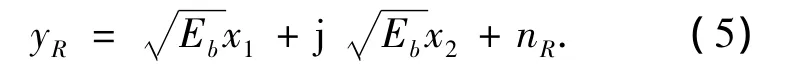
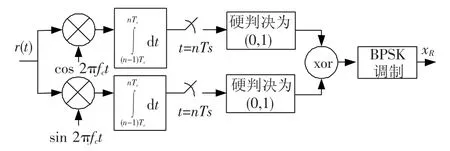
图3 OPNC方案中继节点R的信号处理过程

由于在同相分量和正交分量都有信息，所以需要分2个支路进行处理并分别判决得到2个源信息，然后对2个源信息进行XOR综合，再经过BPSK调制并广播.OPNC对两源信息的综合处理与PNC相同，即(2).下行阶段，节点1和节点2采用与PNC完全相同的处理方法得到对方传输的信息.

当所有信道条件对称时，考虑中继节点R得到XOR信息的错误概率.由于sR=s1⊕s2，当且仅当节点1和2传输的信息中有一个错误的时候，综合信息sR会错.而每个支路的错误概率就是Pe，所以中继节点sR的错误概率为

整个系统的误比特率为

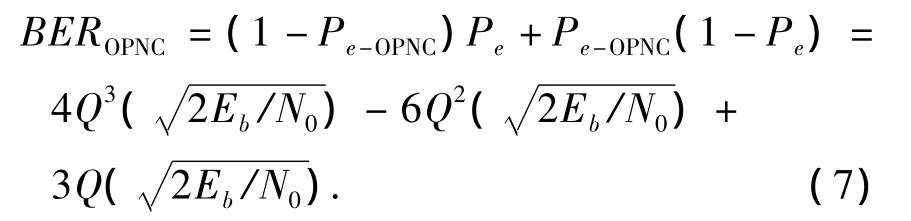
3 联合正交物理层网络编码方案

COPNC方案如图4和图5所示.在上行阶段，节点1和2采用与OPNC方案相同的正交载波，所以节点R收到的基带信号也是(5).仍然采用两支路分别处理并判决得到2个源信息，与OPNC不同的是，COPNC直接对两支路的判决结果进行QPSK调制，不妨以同相支路的输出作为QPSK信号的同相分量，以正交支路的输出作为QPSK信号的正交分量，如图4.COPNC对两路信号的综合处理表达式为

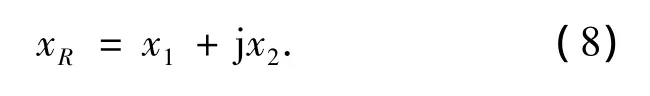
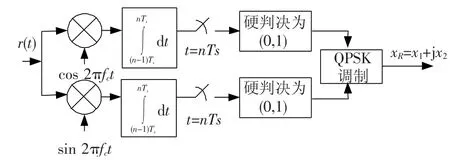
图4 COPNC方案中继节点R的信号处理过程

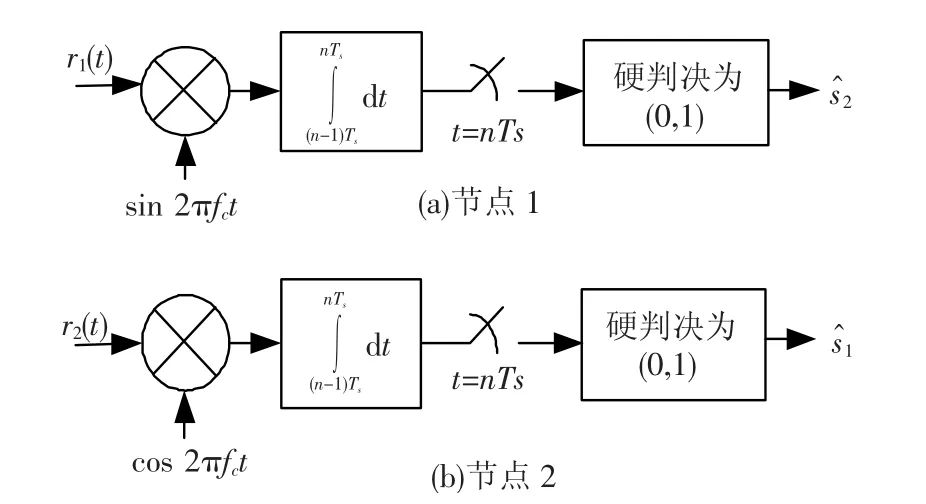
图5 COPNC方案下行阶段节点1和2的信号处理过程

由(8)可以明显看出，COPNC的综合是基于正交信号处理，因此称之为正交综合，对应于文献［1］的XOR和文献［12］的线性综合.由于本方案中两源节点的传输采用正交载波，中继节点采用正交综合，所以称为联合正交物理层网络编码方案.

考虑下行阶段，中继节点R广播QPSK调制信号到目的节点1和2.在节点1，期望得到的信息x2包含于节点R发射信号的正交分量中，所以节点1只需要对接收信号乘以载波sin 2πfct并进行积分、采样以及硬判决即可得到s2的估计值，如图5(a).在节点2，期望得到的信息包含于接收信号的同相分量中，需要乘以载波cos 2πfct以得到s1的估计值.

由于上行阶段采用正交载波，中继节点采用正交综合并在下行阶段以QPSK调制广播，所以在每条信道具有相同的信噪比时，分析系统的误比特率可以单独分析每个信息(s1或s2).考虑信息s1，其在上行阶段以BPSK调制发送到节点R，错误概率为下行阶段，s1包含于QPSK调制信号的同相分量中，被节点2接收，其接收过程与BPSK解调过程一样，所以下行的错误概率仍为.当且仅当上行和下行阶段中其中一个发生错误，s1将会被错误传输.所以

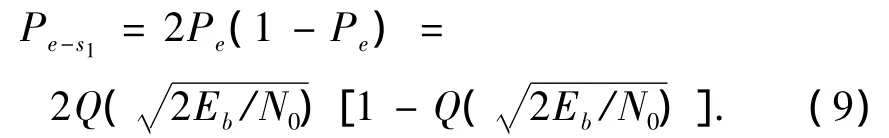
由于s2的误比特率与s1完全一样，所以整个系统的误比特率为

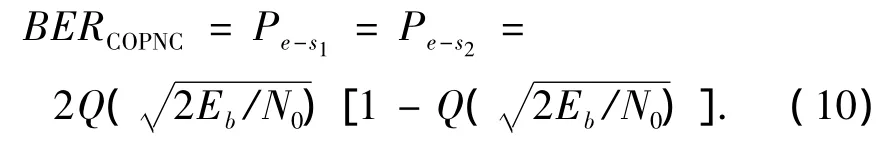
采用COPNC方案的优势分析如下.当上行信道处于低信噪比区间或者两条信道条件不对称，即一条信道信噪比高，一条信道信噪比低的时候，最有可能发生的情况就是在中继节点R两源信息s1和s2其中的一个正确接收，而另一个发生判决错误.在这种情况下，对于PNC和OPNC方案，中继节点R采用XOR的方式将2个信息进行综合，从而得到的综合信息sR是错误的.然后在下行阶段，节点R把sR广播到2个目的节点，如果下行传输不发生错误，则2个目的节点解码出的信息全是错误的.但是对于COPNC方案，由于中继节点采用正交综合的方式(8)，并以QPSK方式进行广播，然后节点1和2只处理携带他们期望得到信息的(正交或同相)分量.所以，节点1和2其中一个可以得到正确的信息，而另外一个得到错误的信息.相比于PNC和OPNC方案中，2个目的节点得到的信息全部错误，很明显，COPNC可以提高TWRC系统的误比特率性能.

4 仿真结果与分析

根据前面对各个方案误比特率性能的分析，由式(4)、(7)和(10)画出 PNC、OPNC 以及COPNC方案在所有信道完全对称的条件下误比特率性能曲线如图6所示.从图中可以看出，在信道条件完全对称时，COPNC方案的误比特率略低于PNC和OPNC方案，3种方案误比特率性能十分接近.

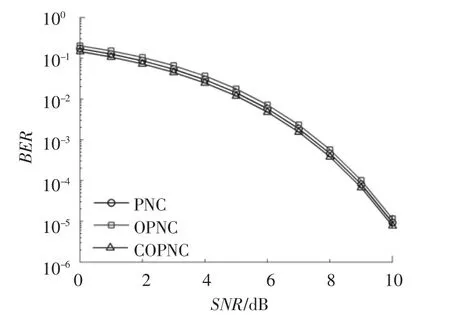
图6 信道条件完全对称时3种方案BER理论值

图7给出了当上行信道与下行信道具有不同的信噪比时3种方案的BER仿真.图7(a)给出的是下行信道具有理想的信道条件(下行SNR=20 dB)，上行SNR从-10 dB到10 dB变化的情况;图7(b)给出的是下行信道不可靠(下行SNR=5 dB)，上行SNR从-10 dB到10 dB变化的情况.可以看出，在这2种情况下，COPNC具有最好的 BER性能，与上一节的分析一致.在图7(b)中，当信噪比大于5 dB时，3种方案的BER性能趋于一致，这是由于此时误比特率主要由不可靠的下行信道决定且3种方案下行信道条件一样.

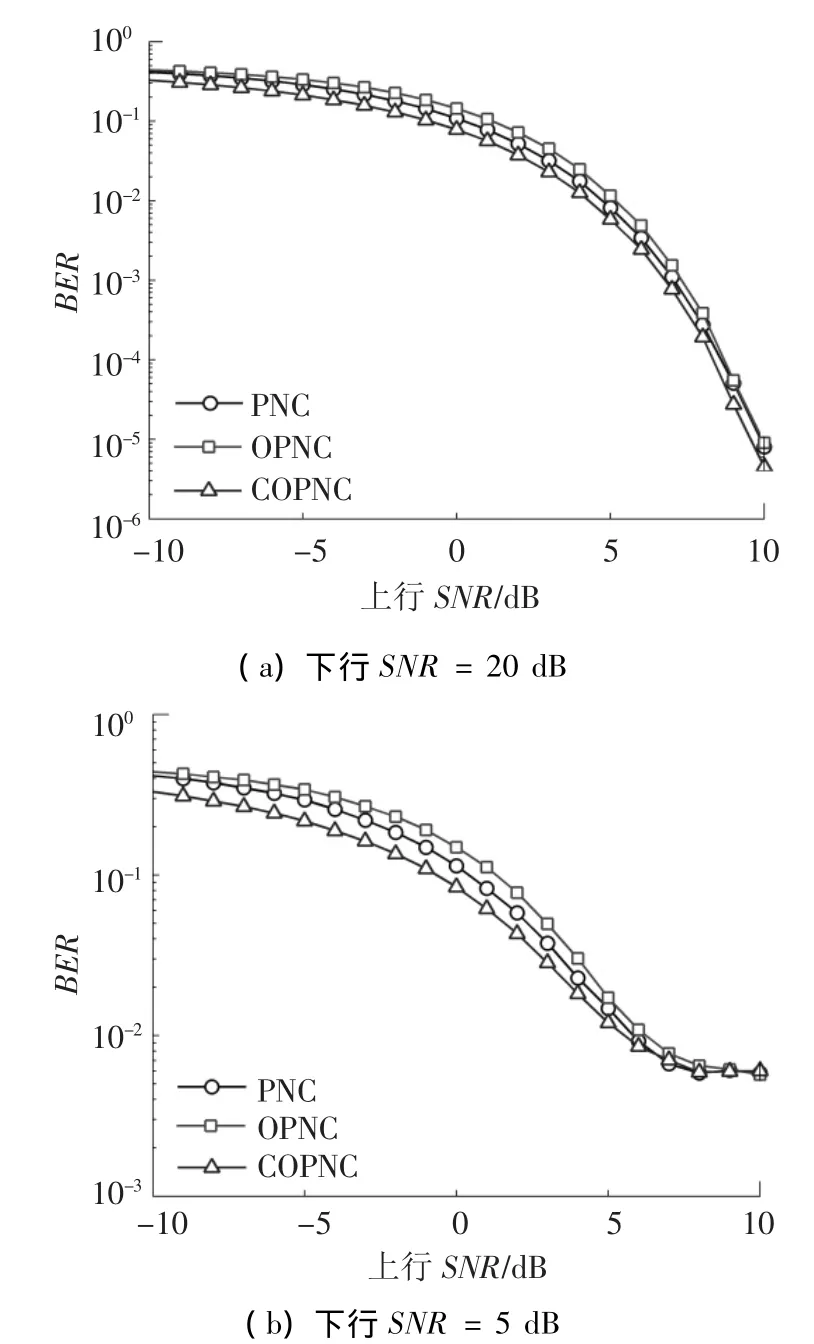
图7 上行信道与下行信道条件非对称时BER仿真结果

当下行信道条件理想(下行SNR=20 dB)，2个上行信道条件非对称时，3种方案的误比特率性能如图8所示.2个上行信道具有不同的信道比，等效于两源节点发射功率不同.不失一般性，假设节点2的发射功率为1，节点1的发射功率为P.对于PNC方案，中继节点R不能继续采用文献［1］中的判决门限与映射方法，这里对于PNC方案，给出一种上行信道非对称条件下基于对数似然比(log likelihood ratio，LLR)的判决与映射算法.在一个符号周期内，LLR的计算为判决及映射方法为

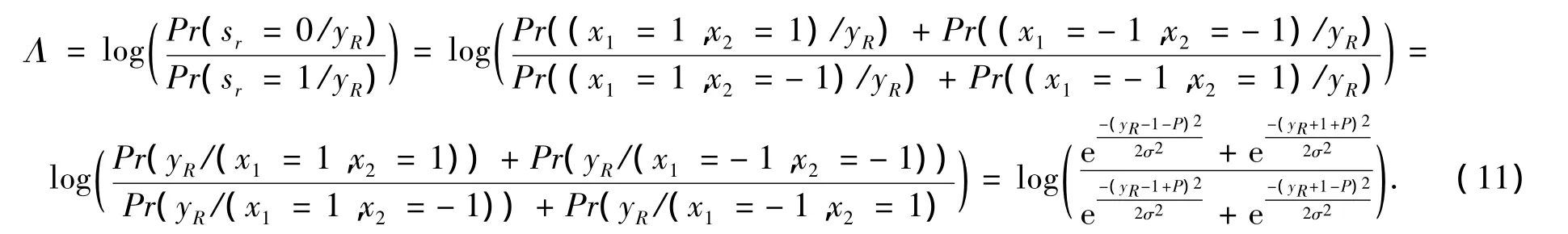
判决与映射算法

图8(a)给出了当SNR2R固定在20dB，SNR1R从-10dB变化到10dB时3种方案的BER性能.从图中可以看出，与其他2种方案相比，COPNC方案仍然具有最低的误比特率.特别是当SNR1R＜5dB时，COPNC的BER明显低于其他2种方案，这是由于当SNR1R落入这个信噪比区间时，节点1发射的比特经常会发生错误，而由于节点2到节点R的信道条件是理想的，节点2发射的比特不会发生错误，如第3节分析的一样，PNC和OPNC方案此时两目的节点都接收到错误的比特，而COPNC方案只有一个目的节点接收到错误比特，另一个节点接收正确的比特.COPNC方案的误比特率会明显低于其他2种方案.

图8(b)给出了当SNR2R固定在5dB时的情况，这时，源节点2发射的比特s2经常发生错误.在这种情况下，与其他2种方案相比，COPNC方案仍然具有最好的BER性能，特别是当SNR1R＞5 dB时，此时系统的误比特率主要由节点2到中继R的上行不可靠信道条件决定.此时源节点1发射的比特s1可以被节点R正确接收，由于下行信道理想，对于COPNC方案，目的节点2就可以收到正确的比特s1，而对于其他2种方案，2个目的节点都将会接收到错误的比特.从图8(b)中可以看出，COPNC的误比特率约等于其他2种方案误比特率的一半.

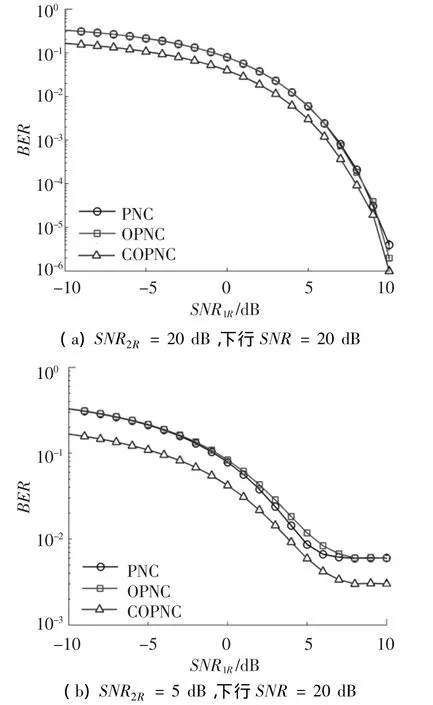
图8 2个上行信道条件非对称时BER仿真结果

5 结论

1)提出了一种新的物理层网络编码方案，称为联合正交物理层网络编码。方案中2个源节点采用正交载波发送信息，中继节点对信息采用正交综合并以QPSK调制的方式将综合信息广播到两目的节点.

2)通过对称信道下的BER性能理论分析和非对称信道下的BER仿真实验，可以看出:当信道条件完全对称时，COPNC方案的误比特率性能略好于PNC和COPNC方案，三者非常接近;当双向中继通信系统的上行信道与下行信道条件不对称时，COPNC方案可以获得最优的BER性能;当下行信道理想，两上行信道条件不对称时，COPNC的误比特率约为PNC和OPNC案的一半，与理论分析吻合.

3)COPNC方案特别适合应用于上行信道非对称的双向中继通信系统系统.

［1］ZHANG Shengli，LIEW S C，LAM，P P.Hot topic:physical-layer network coding［C］//Proceedings of MobiCom’06，New York:ACM，2006:358－365.

［2］ LIEW S C，ZHANG Shengli，LU Lu.Physical-layer network coding:tutorial，survey，and beyond ［EB/OL］.(2011).http://arxiv.org/abs/1105.4261.

［3］ SHANNON C E.Two-way communication channels［C］//Proceedings of Berkeley symposium on mathematical statics and probability.Berkeley:UC Berkeley，1961，1:611－644.

［4］ PAPADOGIANNIS A，BURR A G，TAO Meixia.On the maximum achievable sum－rate of interfering twoway relay channels［J］.IEEE Communication Letters.2012，16(1):72－75.

［5］ LIU，Jianquan.，TAO，Meixia.，XU，Youyun，et al.Superimposed XOR:a new physical layer network coding scheme for two-way relay channels［C］//Proceedings of Globecom’09，Hawaii:IEEE Press，2009.

［6］WANG Lei，WU Zhuo.BER Analysis of Physical Layer Network Coding with PSK Modulations for Two-Way Relay Channels ［C］//Proceedings of IEEE International Conference on Signal Processing，Communication and Computing(ICSPCC’12)，Hong Kong:IEEE Press 2012:484－489.

［7］ XIONG Wenhao.Orthogonal physical layer network coding［D］.Wichita，USA:Wichita State University，College of Engineering，2009.

［8］LIEW S C，ZHANG Shengli，LU Lu.Physical-layer network coding:tutorial，survey，and beyond ［EB/OL］.Physical Communications.(2012).http://www.sciencedirect.com/science/article/pii/S1874490712000419.

［9］ZHANG Shengli，LIEW S C，LAM P P.On the synchronization of physical-layer network coding ［C］//Proceedings of Information Theory Workshop(ITW 2006)，Chengdu:IEEE，2006:404－408.

［10］LU Lu，LIEW S C.Asynchronous physical-layer network coding［J］.IEEE Transactions on Wireless Communications.2012，11(2):819－831.

［11］PROAKIS J，SALEHI M.Digital communication(5th Edition)［M］.New York:McGraw-Hill，2008:190-193.

［12］YANG Hongjuan，MENG Weixiao，LI Bo.Performance analysis of amplify-and-forward cooperative diversity with multiple-antenna nodes via analog network coding ［J］.Journal of Harbin Institute of Technology(New Series).2013，19(6):13-16.