空间机器人多臂精准协同控制技术

贺 亮，王有峰，吴 蕊，谢 冉

(1.上海航天控制技术研究所，200233上海;2.上海市空间智能控制技术重点实验室，200233上海;3.北京航空航天大学宇航学院，100191北京)

近年来，以在轨服务技术为代表的空间应用领域得到了突飞猛进的发展，为了夺取技术制高点，各航天强国都投入巨资开展关键技术攻关.目前，以美欧为代表的航天强国已经完成了诸如模块更换、在轨组装以及燃料加注［1-2］等项目的空间演示验证，并且继续制定一系列新的计划拓宽在轨服务的内容和手段.

空间机器人作为在轨服务的一种有效手段［3］，尤其受到美德等国的青睐.实践证明，空间机器人由于具有自主、灵活和安全等特点，在抓捕和操作目标的过程中表现出了其它工具所不具备的独特优势，因此更加适合对精度要求较高的在轨服务项目.

空间机器人按机械臂的数量可以划分为单臂空间机器人和多臂空间机器人.随着任务复杂程度的不断增加，单臂空间机器人将不能满足对操作精度要求较高的在轨服务任务，相反，多臂空间机器人则能较好地满足此类任务的需求，通过多条机械臂协同工作，快速灵活地完成抓捕、更换以及拖曳等操作.目前，国外已经制定了多项多臂空间机器人的研究计划，典型的有美国的SUMO/FREND 计划［4］、NM-5计划以及凤凰计划.这些计划都涉及到一项核心技术——机械臂协同控制技术，本文正是以此为背景，进行空间机器人多臂精准协同控制技术研究.

多臂空间机器人由于工作在零过载、微重力的空间环境中［5-6］，故安装在其上的机械臂通常设计为轻柔的细长杆型结构，这使得它成为一种典型的多柔体系统;同时，由于机械臂运动产生的反作用力和力矩会改变本体的位置和姿态，即机械臂和本体之间存在着运动学和动力学耦合，导致地面固定基座操控平台的控制技术不能直接应用到多臂空间机器人上［7-8］，因此需要利用多柔体系统动力学［9］的理论和方法建立柔性多臂空间机器人动力学模型.

在空间机器人建模方面，国内外学者已经取得了许多研究成果，典型的有美国的VAFA Z和DUBOWSKY S提出的虚拟机械臂(VM)概念［10］中国的梁斌提出的动力学等价机械臂［11］以及李瑰贤等［12］采用牛顿-欧拉法建立的动力学方程.为了得到更具普遍性的结果，本文采用Kane方法建立系统动力学模型.

1 系统建模

1.1 系统构型

本文研究的空间机器人包含3条机械臂，每条机械臂由7节构成，其构型如图1所示.

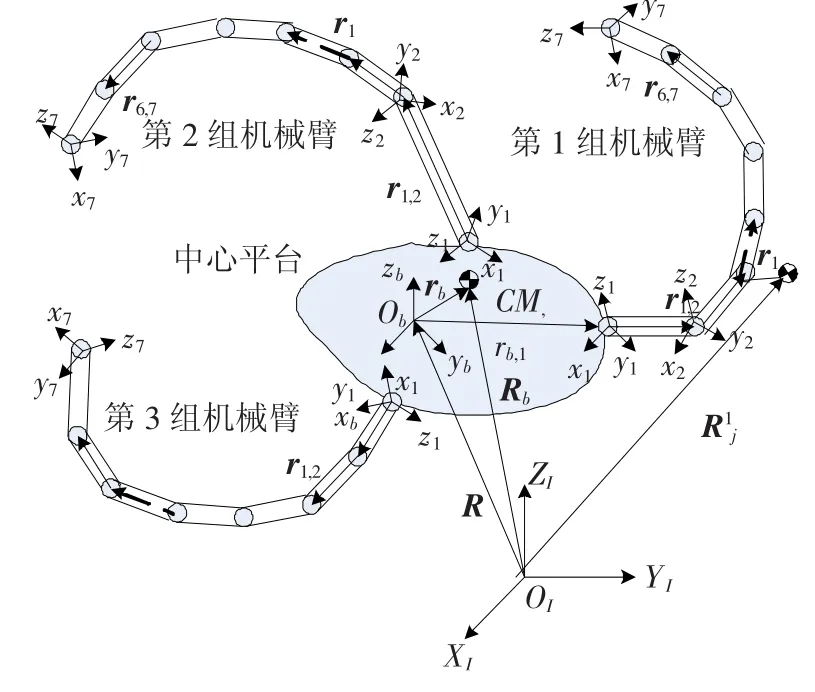
图1 多臂空间机器人构型

1.2 基本参数定义

1.2.1 坐标系单位基向量

1)中心体连体坐标系Sb(Obxbybzb)

原点Ob位于中心体质心，xb、yb和zb与中心体惯性主轴平行且满足右手定则.

设系统有i条机械臂，第i条臂有ni节，定义第i条臂中第j节臂的机械臂坐标系原点位于第j节臂与其内接体的铰链oi j处，坐标系各轴与第j节臂固连.

1.2.2 位置参数定义

接下来给出图1中各矢量的定义:

1.2.3 运动参数

1.2.3.1 角速度

1.2.3.2 线速度

1)中心体线速度

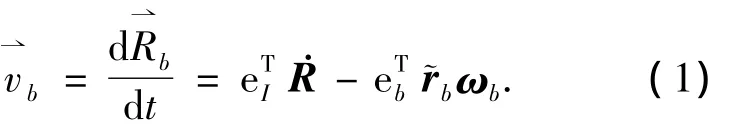
2)第i条机械臂线速度不妨以j＞2为例，对R⇀i j求导，j=1 时同理可得

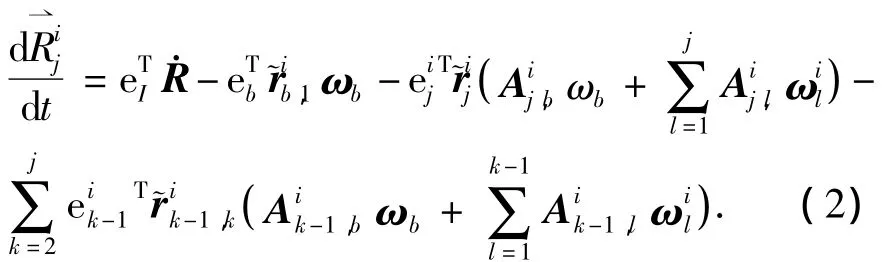
1.2.3.3 加速度

1)中心体质心加速度

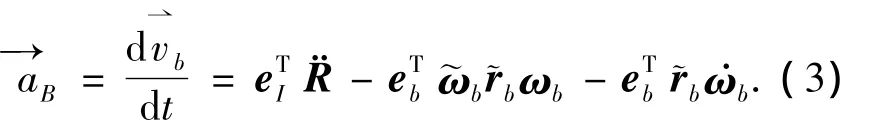
2)第i条机械臂(以j＞2为例j=1时同理)

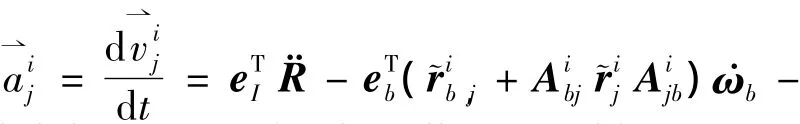
1.3 多臂空间机器人Kane方程

1.3.1 引理

理想约束条件下，系统若处于平衡，则

这个方程就是Kane方程，式中f*Ⅰk，f*ek和f*Nk分别称为系统与偏速度Wk对应的第k阶广义惯性力、广义主动力和广义弹性力.

1.3.2 机械臂系统参数计算

1.3.2.1 广义惯性力

1)中心体惯性力

中心体第1阶广义惯性力为

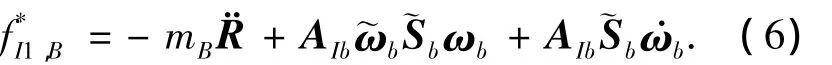
中心体第2阶广义惯性力为

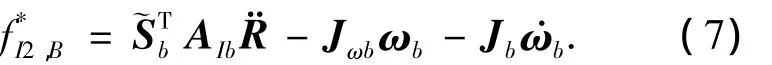
中心体第k(k＞2)阶广义惯性力为

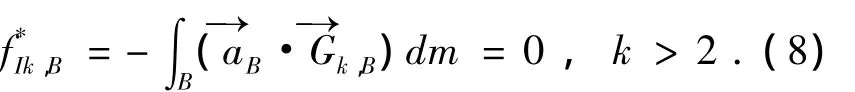
1.3.2.2 第i条机械臂第j节臂的惯性力

1)第1阶广义惯性力

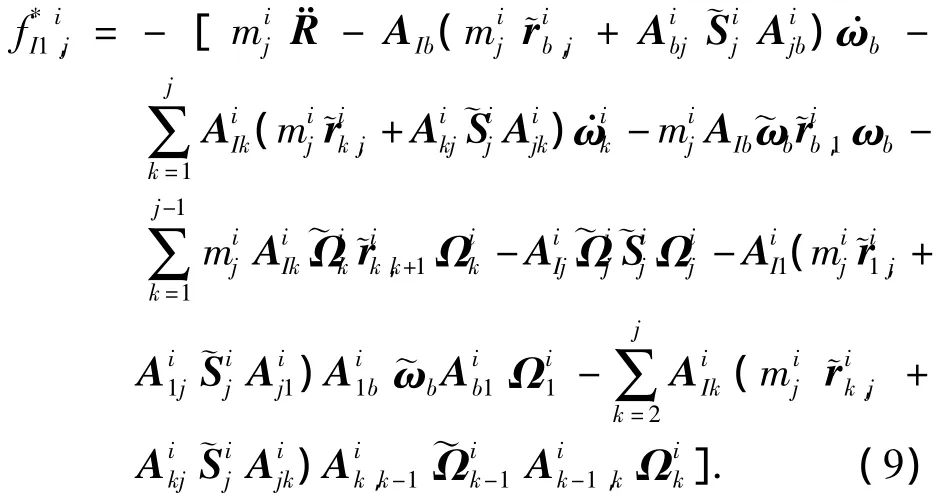
2)第2阶广义惯性力

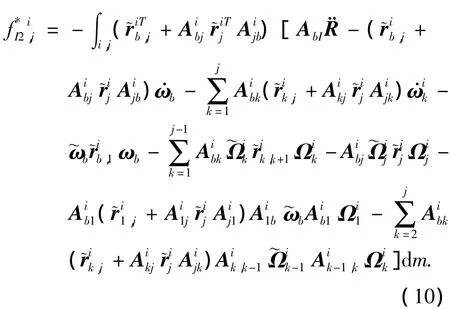
3)第2+7*(i-1)+l阶广义惯性力

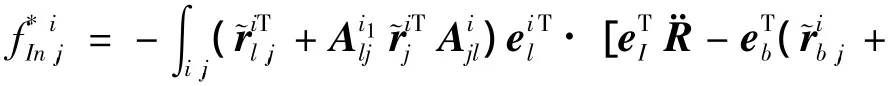
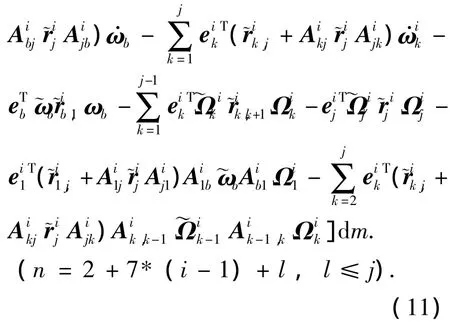
1.3.2.3 广义主动力

系统所受外力主要包括以下3个部分:

1)作用于中心体上的力F;

2)作用于中心体上的力矩T;

3)作用于机械臂各关节处的控制力矩，对应于第i条机械臂第j节臂的关节处的控制力矩记为Tij.

1.3.3 空间机器人各体动力学方程

1.3.3.1 中心体平动方程

中心体平动方程对应于第1阶广义速度R，将式(6)和式(9)式代入式(5)，因此有

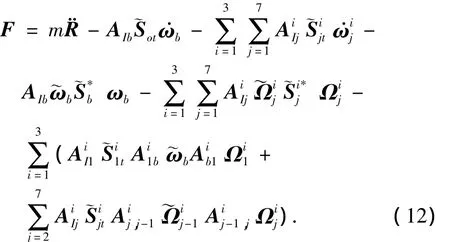
1.3.3.2 中心体转动方程

中心体转动方程对应于第2阶广义速度ωb，将式(7)和式(10)式代入式(5)，因此有

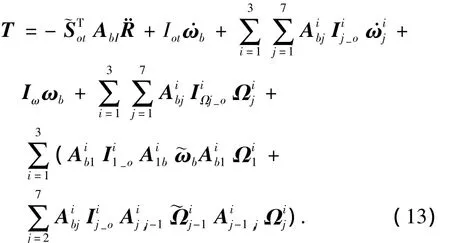
1.3.3.3第i条机械臂第j节臂的转动方程

第1节臂转动方程对应于第2+7*(i-1)+1阶广义速度ωi1，将(8)和(11)式代入(5)，因此有

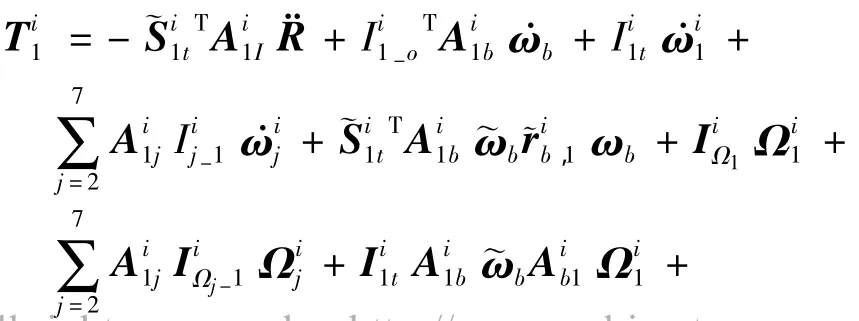
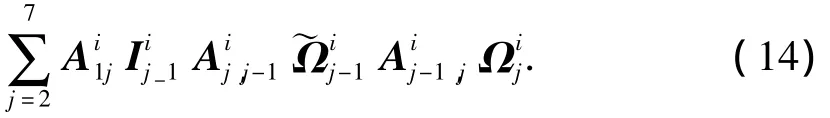
其他各节臂转动方程类似，不再重复.

1.3.4 空间机器人系统矩阵形式完整动力学方程将中心体平动方程和转动方程整合得到机械臂系统的动力学方程为

2 开链系统控制器设计

空间机器人轨迹跟踪控制方面，国内外学者已经取得了大量研究成果，典型的有YOSHIDA K等［13］人提出的双臂补偿控制方法和林成金［14］提出的轨迹跟踪鲁棒控制方法.这些方法需要进行繁琐的矩阵运算，难以实现机械臂轨迹实时跟踪控制，为此，本文基于李雅普诺夫稳定性理论，推导得出了较为简洁的控制算法，详细过程如下文.

2.1 动力学方程简化

在控制器设计过程中，忽略质心平动运动的影响，同时考虑到机械臂的运动过程一般比较缓慢，中心体的角速度一般也是小量，因此方程中的非线性耦合项可以作为高阶小量忽略不计，于是系统动力学方程可以重新写成下述的线性形式:

式中:

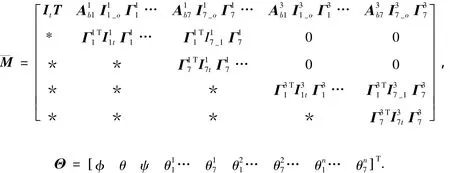
小角度假设下有

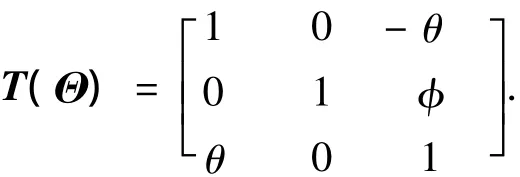
式(16)虽然形式上很简洁，但实际上系统质量矩阵与机械臂各关节转角相关，且计算表达式非常复杂，但考虑到整个系统运动较为缓慢，且机械臂的质量和惯量较小，因此可采用“冻结系数法”来计算质量阵.记更新时间段之内M的常值取为，则该时间段内控制器设计模型为

不同时段内除Mc的取值不同外，系统模型形式无变化，选取式(17)作为控制方程.

2.2 控制律设计

定义状态量为实际值与期望值之间的误差为

取中间变量

式中:K为对称的正定矩阵.取Lyapunov函数

则有

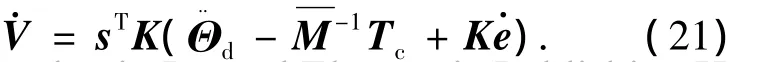
取控制力矩

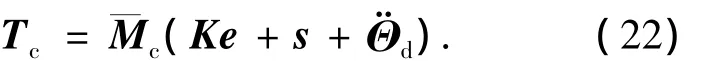
得到

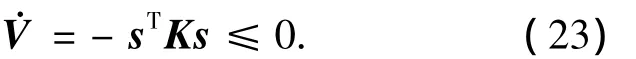
从而说明函数V是定负的，因此由式(23)可知，函数V的解对t的全导数是定负的，也即说明该控制律能够保证误差收敛且是渐近收敛的.

3 数值仿真

首先给出多臂多自由度机械臂系统的仿真参数，表1给出3条机械臂在中心体上的安装位置.

表1 3条机械臂在中心体上的安装位置

表2给出第1条臂第2～7节的安装位置，由于3条机械臂完全相同，故在此只给出其中1条的数据.

表3给出中心体、各条机械臂以及目标的质量特性参数，3条机械臂完全相同，只给出第1条臂的参数.

给定中心体姿态角初始状态为［2 3 2］Tdeg，第一条臂各关节相对于标称状态的初始转角为［-7.02 155.24-142.08-13.15-3.37 0 0］Tdeg，中心体和机械臂各关节角速度均为零，考虑到实际控制力矩的大小有限，限定中心体的最大控制力矩为umax-b=［100100100］TN·m，各关节最大控制力矩为50 N·m，利用Matlab仿真得到结果如图2～5所示.

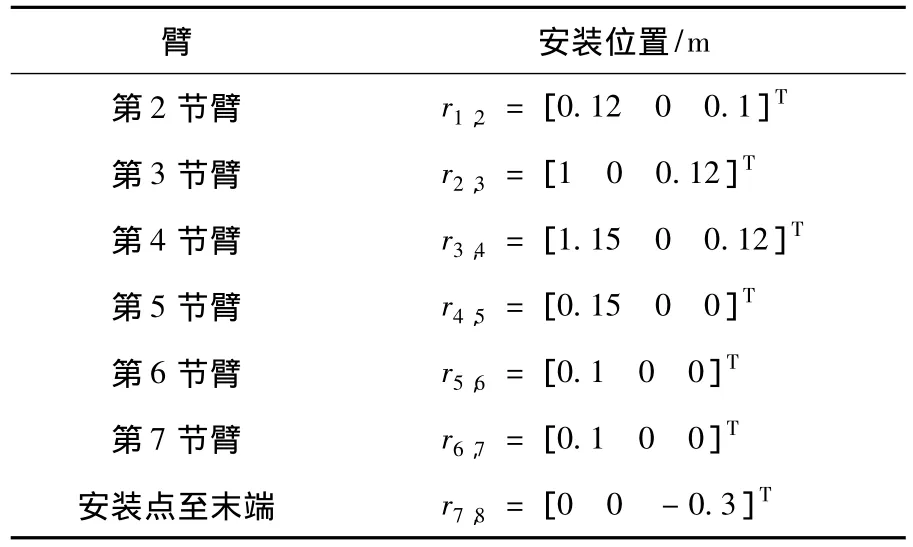
表2 第1条臂第2～7节的安装位置

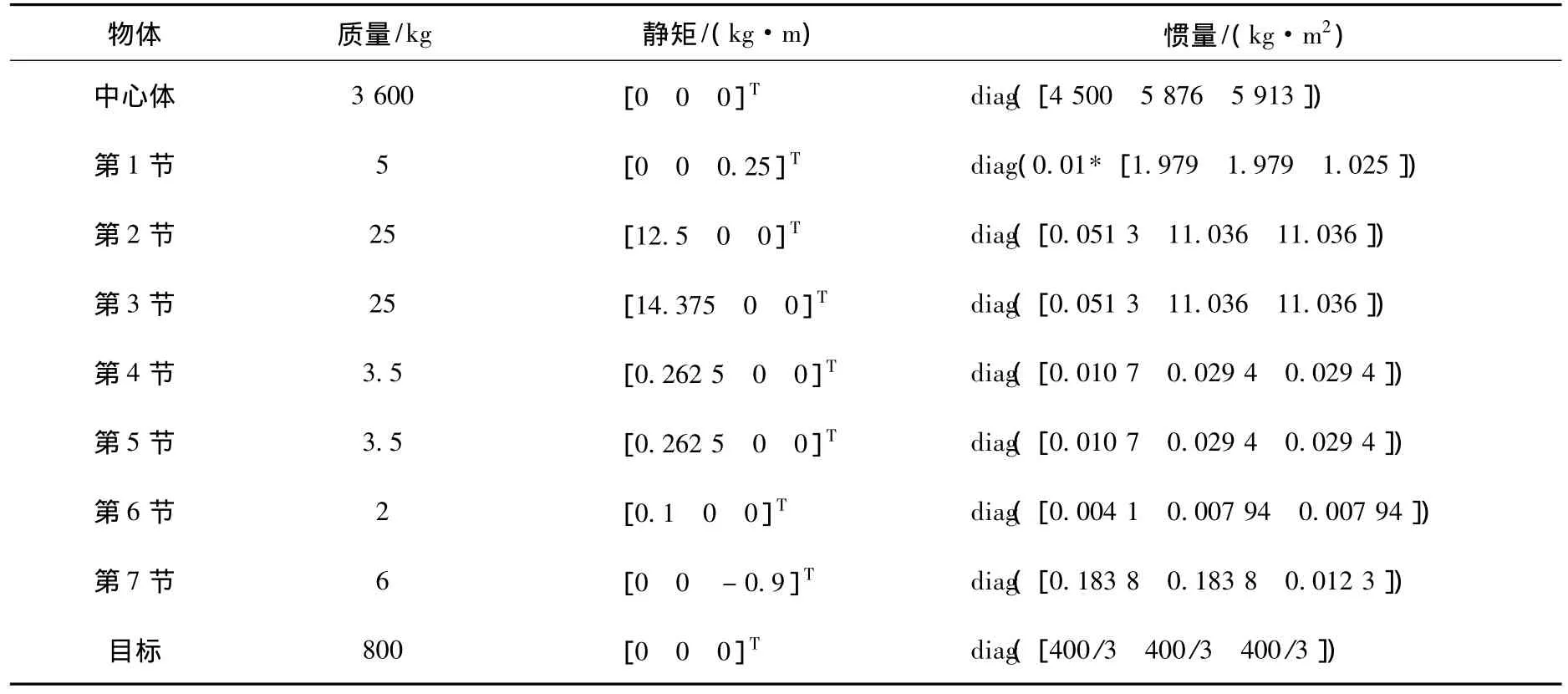
表3 中心体、第1条机械臂各节以及目标的质量特性参数

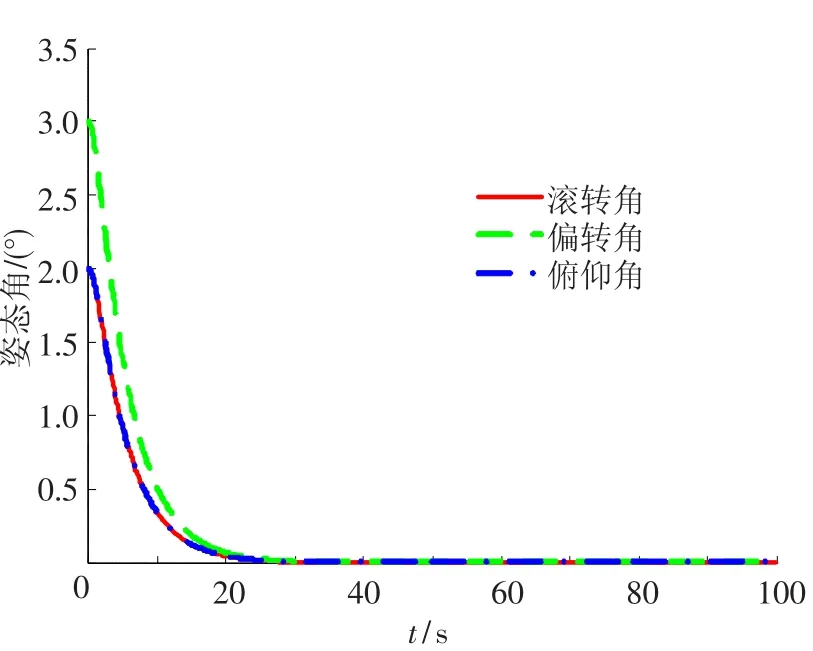
图2 中心体在控制力矩作用下姿态角变化曲线

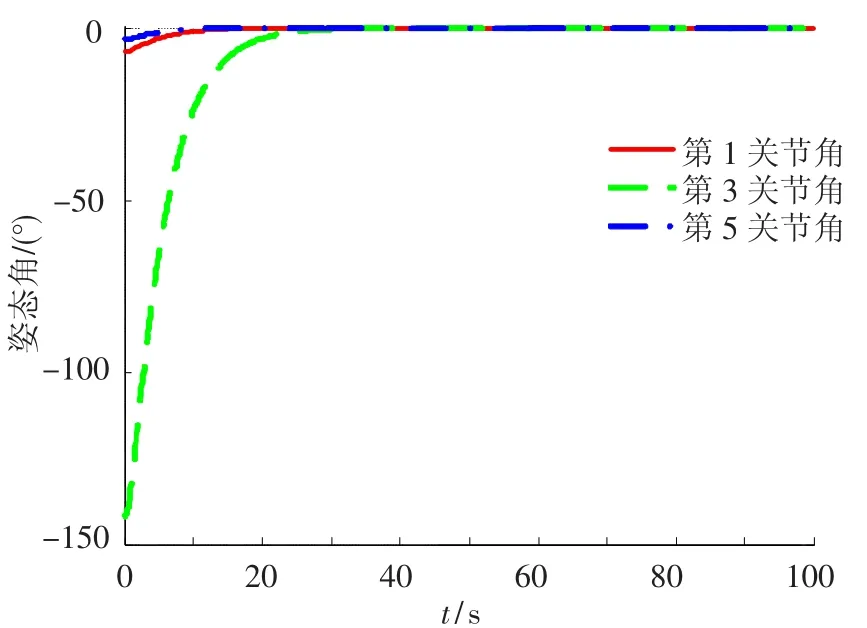
图3 第1条臂第1、3、5关节角在控制力矩作用下的变化曲线

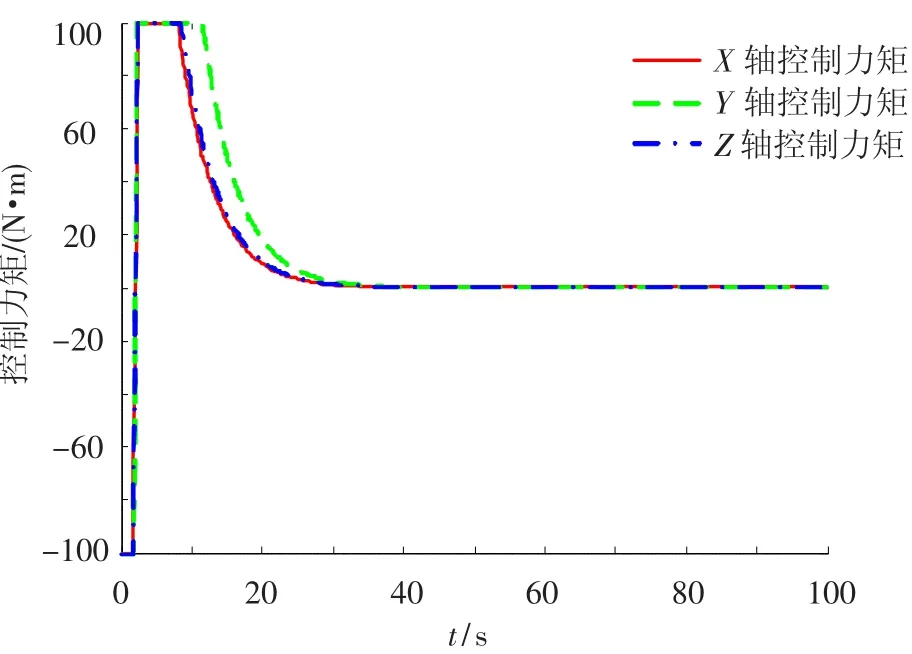
图4 中心体所受的控制力矩变化曲线

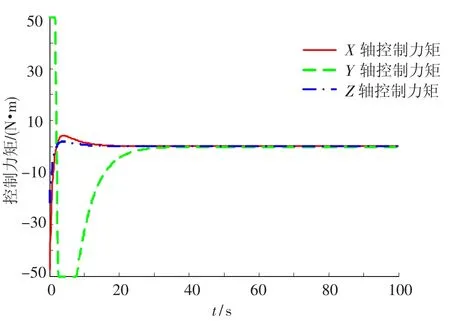
图5 第1条臂第1、3、5关节所受的控制力矩变化曲线

第2、4、6关节的仿真结果类似，文中不再给出.从图2至图5可以看出，在控制力矩受约束的情况下，最终平台姿态和关节转角都能很好的跟踪期望值(姿态角和关节转角的期望值都取为零)，并且姿态角控制精度达到了1×10-9rad，与梁斌［10］提出的动力学等价机械臂(DEM)方法相比，具有更高的控制精度，与林成金［13］提出的轨迹跟踪鲁棒控制方法相比，具有更高的稳定.

4 结论

1)利用Kane方法建立了具有3条7自由度的空间多臂机器人动力学方程，并且只要改变模型中的求和上限，即可改变机械臂的数量和自由度所得的结果可以推广到具有n条m个自由度的空间机器人，n，m∈Z.

2)针对开链情况下中心体和机械臂的协同控制问题，设计了基于李雅普诺夫函数的机械臂运动跟踪控制律，实现了机械臂在三维空间抓捕目标过程中对期望轨迹的跟踪.

3)通过数值仿真可知，本文所设计的控制律其他方法相比具有更高的控制精度和稳定性，并且在力矩大小受限与不受限两种情况下均能实现机械臂末端轨迹跟踪.

4)本文所建立的模型具有一定的开放性，只要在现有模型中加入弹性坐标系即可将模型转化为柔性机械臂系统，而不需要重新推导方程.

［1］李广兴，肖余之，卜劭华等.空间站组装过程姿态控制方案研究［J］.载人航天，2012，18(01):22-29.

［2］敬忠良，袁建平.航天器自主操作的测量与控制［M］.中国宇航出版社，2011.

［3］LANIUS R，MCCURDY H.Robots in Space［M］.Baltimore:The Johns Hopkins University Press，2008:1-2.

［4］BOSSE A B，BARNDS J W，BROWM M A.SUMO:spacecraft for the universal modification of orbits［J］.Proc.of SPIE，2004，5419:36-46.

［5］MURARD S.Extended online nonholonomy criterion of a drifted free-flying space robot with-without Interaction with a target satellite［C］//IEEE/ISIE2006，Montreal，2006:80-85.

［6］朱战霞，袁建平.航天器操作的微重力环境构建［M］.中国宇航出版社，2013:13-16.

［7］KAZUYA Y.Engineering test satellite VII flight experiments for space robot dynamics and control:theories on laboratory test beds ten years ago，now in orbit［J］.The International Journal of Robotics Research，2003，22(5):321-335.

［8］KATSUHIKO Y.Attitude control of space robot by arm motion［J］.Journal of Guidance，Control and Dynamics，1994，17(5):1050-1054.

［9］杨乐平，朱彦伟，黄涣.航天器相对运动轨迹规划与控制［M］.国防工业出版社，2010.

［10］VAFA Z，DUBOWSKY S.The kinematics and dynamics of space manipulators:the virtual manipulator approach［J］.Journal of Robotics Research，1990，9(4):3-21.

［11］梁斌，刘良栋，李庚田等.空间机器人的动力学等价机械臂［J］.自动化学报，1998，24(6):761-767.

［12］李瑰贤，袁景阳，柳长安.多臂自由飞行空间机器人协调操作动力学分析［J］.哈尔滨工业大学学报，2007，39(3):374-377.

［13］YOSHIDA K，KURAZUME R，UMETANI Y.Torque optimization control in space robots with a redundant arm［J］.IEEE/RSJ In Workshop on Intelligent Robots and Systems，1991:1647-165.

［14］林成金，陈力.自由漂浮双臂空间机器人基于速度滤波器的惯性空间轨迹跟踪鲁棒控制［J］.空间科学学报，2012，32(5):757-764.