摩擦系数对高副接触磨损影响的有限元模拟

张优云，陈 朝，朱永生，蒋翔俊

(西安交通大学现代设计与轴承转子系统教育部重点实验室，710049西安)

磨损占机械零件失效的60%～80%［1］，因此，研究磨损具有非常重要的意义.随着计算机技术的发展，数值仿真技术已经成为磨损研究的一种非常重要的手段.蒋翔俊等［2］利用数值仿真方法研究了不同交变载荷力作用下燃机端面齿的磨损规律.在数值仿真研究方法中，有限元仿真分析已经在工程中得到了广泛的应用，并且在磨损分析方面具有很强的实用性［3］.冯伟［4］利用有限元方法进行滑动磨损试验的摩擦学仿真研究.Sfantos等［5］、Andersson等［6］提出了应用边界元法及有限元方法的磨损预测方法.Rezaei等［7］利用有限元方法和Archard方程，建立了径向滑动轴承磨损过程的模型.Cruzado等［8］利用商用有限元软件ABAQUS，研究了钢丝绳的微动磨损，并且进行了试验验证.宿月文［9］利用有限元方法进行了滑动磨损过程的仿真研究，对销轴的磨损进行了预测.但是上述研究只能对长距离的滑动磨损进行仿真，而不能对小幅振动下的磨损进行有效的仿真.摩擦系数、接触压力和滑移量等特征参数是影响磨损的主要因素［10］.在磨损过程中，摩擦系数并不是一个恒定的值，而是随着磨损循环次数的增加而逐渐增大，最终在一个较小的范围内波动［11］.在目前的磨损有限元仿真中，针对变化的摩擦系数的影响研究并不多见.

本文建立了一种基于有限元方法的磨损预测模型，利用有限元软件ANSYS12.1对圆柱和平板相接触的小幅振动磨损过程进行了仿真分析，将仿真结果与文献［11］中的实验数据进行了对比验证，并利用该模型分析了摩擦系数的变化对磨损量、接触压力、滑移量、正应力、剪应力的影响.

1 磨损分析的有限元建模

1.1 接触分析

圆柱和平板的接触问题广泛应用于磨损的研究中，其接触情况如图1所示.根据赫兹接触计算公式，可以得到接触压力的分布为

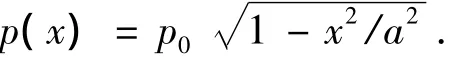
式中，接触区域半宽度a为

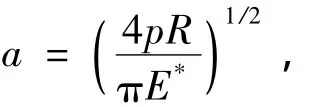
最大接触压力p0为

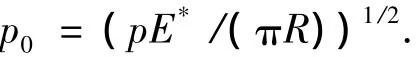
其中

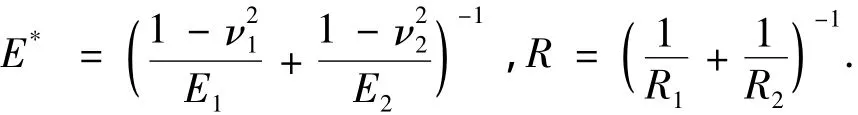
式中，E1和E2、ν1和ν2、R1和R2分别为两个接触体的弹性模量、泊松比和曲率半径.

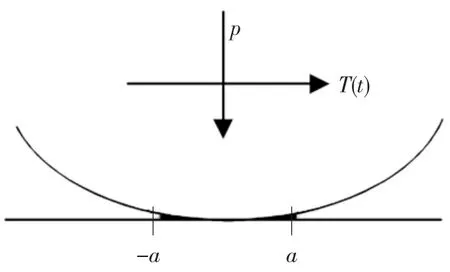
图1 圆柱和平板的接触

在有切向力T(t)的作用下，两个接触表面间会出现相对滑动.在整体滑移的情况下，切向力的最大值Tmax和摩擦力μp相等(μ为摩擦系数).如果Tmax＜μp，则会产生局部滑移.此时，接触区域的中心会产生一个半宽度为c的粘着区，而在c≤｜x｜≤a的区域则会产生一个局部滑移区.瞬时时刻的粘着区的宽度c*可以表示为

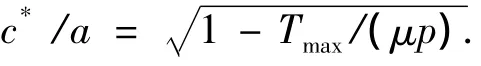
1.2 有限元模型

本文针对的材料与文献［11］相同，为高强度合金钢.由于圆柱和平板的接触属于线接触，因此可以将接触模型简化成二维模型.图2是磨损仿真的有限元模型.

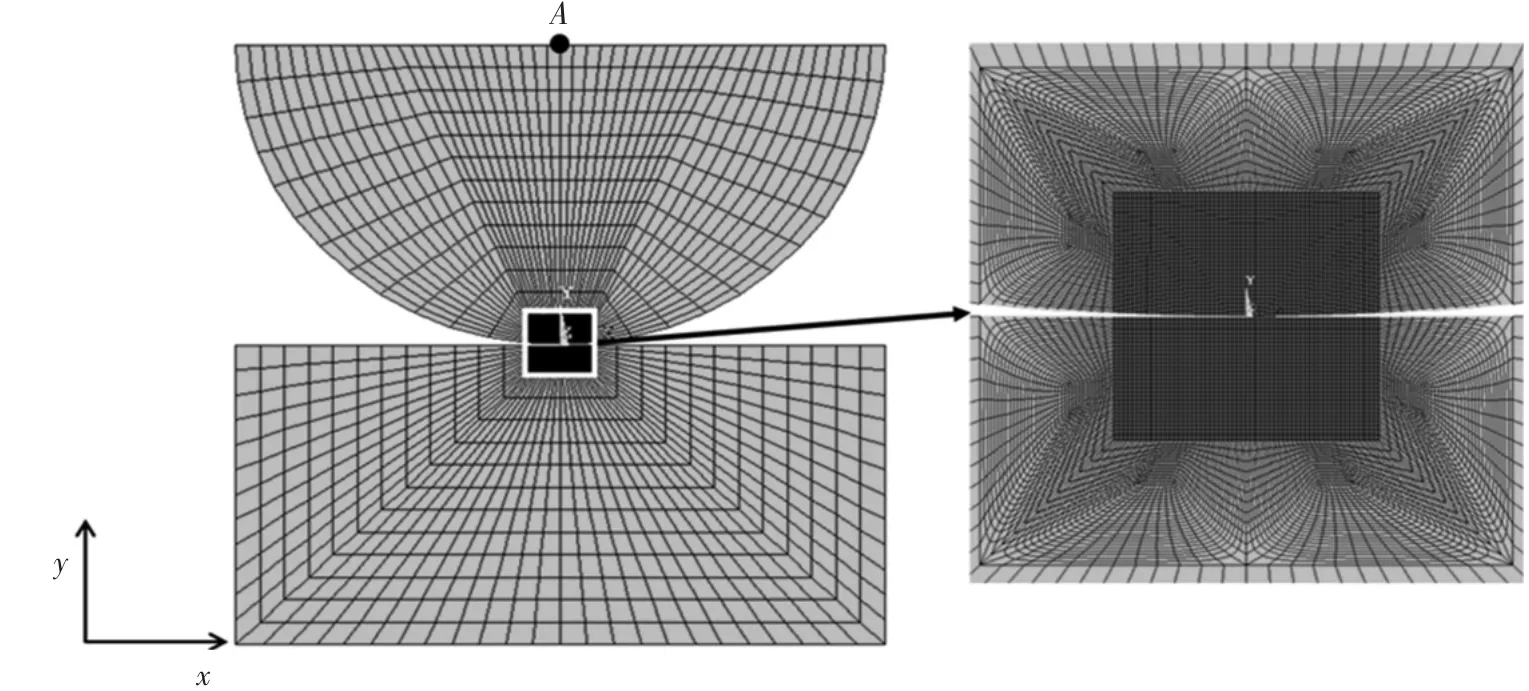
图2 圆柱和平板接触的有限元模型

半圆和矩形的单元类型均为PLANE42，弹性模量为200 GPa，泊松比为0.3，摩擦系数为0.8.接触区域的半宽度设置为0.3 mm，这一宽度是根据赫兹接触计算所确定的.为了得到比较精确的计算结果并尽可能的减少节点数量，划分网格时只将接触区域的网格细化(网格宽度为5 μm).为了使网格划分较细的区域和网格划分较粗的区域能够平稳的过渡，该模型在两个区域之间增加了一个过渡区.节点总数为24 004个.本模型使用接触单元CONTA172和目标单元TARGE169来定义接触对.但是ANSYS只能保存接触单元的计算结果.为了能将相互接触的两个面的数据都提取出来，该模型定义了两个接触对，即以接触区域中上方的圆弧为接触面、下方的直线为目标面的接触对，和以直线为接触面、圆弧为目标面的接触对.圆柱在平板上的运动方式与文献［11］中的实验相同，即以坐标原点为中心，沿x方向作往复运动，幅值为25 μm.

1.3 磨损计算模型

Archard磨损模型是一种经典且应用非常广泛的磨损计算模型.该模型可表述如下:

式中:V为总的体积磨损量，m3;P为法相载荷，单位为N;S为总的滑动距离，m;H为材料的布氏硬度，Pa;K为磨损系数，是一个无量纲的比例常数.为了体现两接触表面的轮廓随磨损循环进行的变化，研究磨损深度更具实际意义.假设在一个极小的接触区域dA内，有一段较小的滑动距离dS，此时应用式(1)可以得到

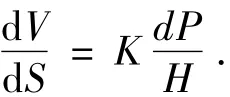
方程两边同时除以dA可以得到

式中，dP/dA为局部的接触压力，它是一个接触点水平位置的函数，记为p(x);dV/dA为局部磨损深度，记为dh;将K/H记为k1，则式(2)可写为

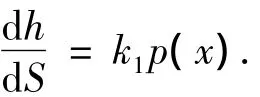
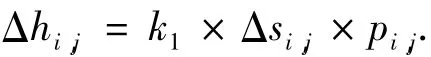
如果将磨损过程离散为若干个子步来计算磨损量，则第i个节点在第j次磨损循环时的磨损增量为式中，k1与材料属性、运行工况等因素有关;Δsi，j是接触区域的滑移量，通常小于实际的滑动距离;接触压力pi，j可通过数值方法，如有限元方法来得到.

1.4 磨损仿真过程

磨损仿真的过程是十分缓慢的，如果完全仿真实际磨损过程的每一步，将耗费大量的资源和时间，而计算精度却不会有太大的提高.本文采用的磨损计算流程见图3.为了提高磨损计算的效率，本文主要采用两种方法:其一，如果将半圆往复运动1次视为1个磨损循环，并且假定n(本文的模型中n=20)次磨损循环内的磨损量都是相等的，这样n次磨损循环的磨损量就可以用1次磨损循环的磨损量的n倍得到;其二，1个磨损循环内半圆滑动的距离是原点到右极限位置距离的4倍，假设1个磨损循环内产生的磨损量是半圆动到右极限位置所产生的磨损量的4倍，这样也可以在保证计算精度的情况下提高计算效率.在施加y方向向下的载荷时，如果直接将一个集中力施加在A点位置的节点上，则会导致受集中力作用的区域产生变形，且受力情况与实际不符.为了避免这一情况，本文用CERGID命令将A点处的节点和y坐标值与其相等的节点耦合，形成一个刚性区域，这样在半圆圆心的节点处施加集中力载荷时，就是通过整个刚性区域来传递载荷了.平板的底部和两边都添加了x和y方向上的位移约束，使之在仿真过程中固定不动.

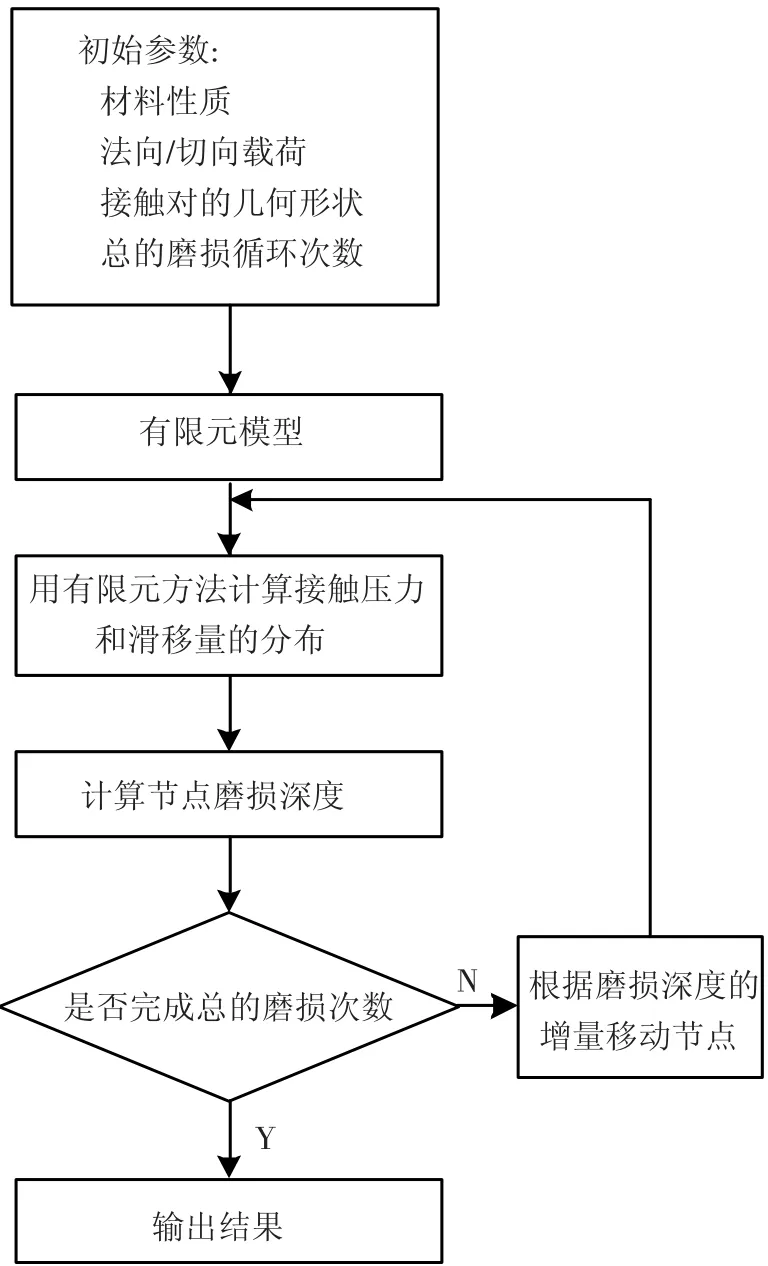
图3 磨损计算流程图

在添加好约束，并在A点施加了y方向向下的载荷后，进入后处理器，将接触区节点的数据提取出来.提取的数据主要包括节点的x坐标、y坐标、压力和滑移量.然后再在A点对圆柱施加x方向向右的位移载荷.为了提高计算结果的精度，这里不是直接将半圆移动到右极限位置，而是将这个过程分成若干个子步，每进行一个子步之后，提取节点的压力和滑移量，根据Archard方程计算这一子步的磨损量.在所有的子步都进行完之后，将计算的磨损量叠加，就可以得到将圆柱从原点位置移动到右极限位置这一过程的磨损量.如前所述，将这一结果乘以4就可以得到一个磨损循环内的磨损量.再乘以n，即可得到n次磨损循环的磨损量.然后用节点在经历磨损循环前的y坐标值减去其对应的磨损量，得到其磨损后的位置，再将节点移动到各自的新位置，就可以得到磨损后的表面轮廓.最后卸掉所有的载荷.使用循环命令反复进行上述求解操作，就可以得到指定循环次数后的磨损量和磨损后的表面轮廓.

2 有限元仿真结果

图4是在185 N的载荷下，本文的有限元预测模型与赫兹接触理论分别计算出的压力分布.从图中可以看出，这两种计算方法所得到的压力分布很接近，最大压力值的误差为4.67%.

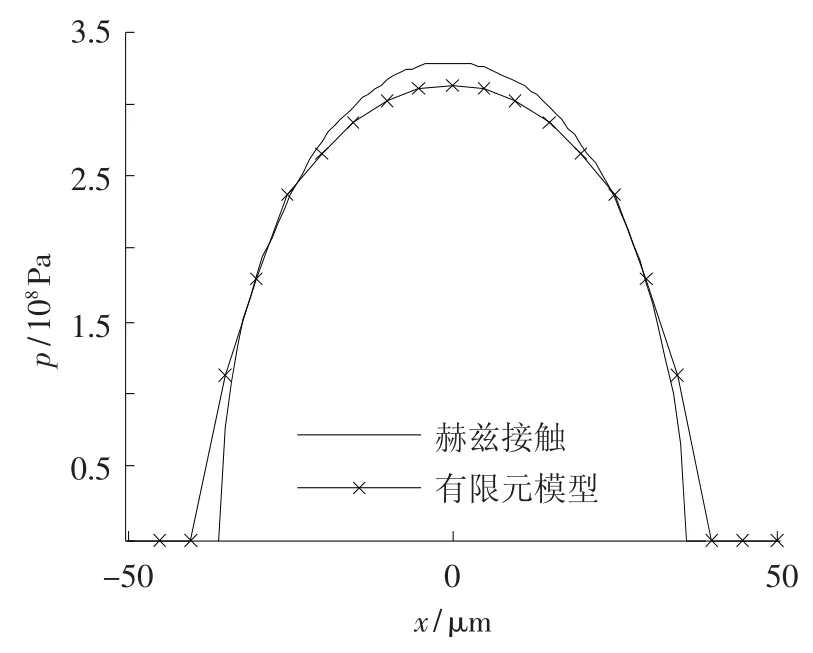
图4 有限元模型与赫兹接触分别计算的压力分布(载荷:185 N)

图5是有限元预测模型在载荷为185 N，往复运动的幅值为25 μm的条件下，不同磨损循环次数后，圆柱和平板的表面轮廓.从图中可以看出，随着磨损次数的增加，两接触表面的磨损深度逐渐增加，接触区域逐渐增大，并且两个表面的接触区的宽度非常接近.

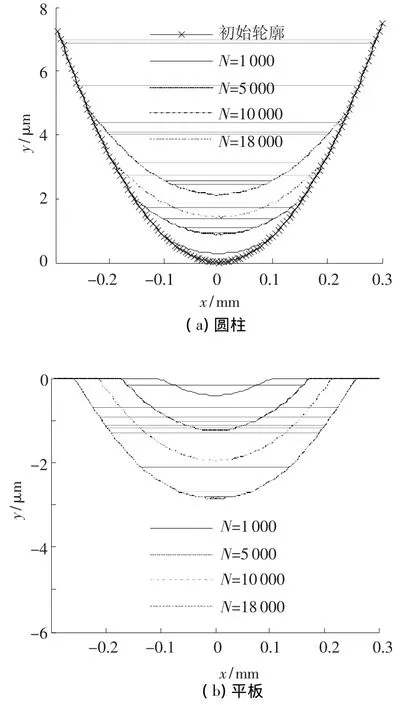
图5 不同磨损循环次数后的表面轮廓(载荷:185 N，幅值:25 μm)

图6是在载荷为185 N，往复运动幅值为25 μm的条件下，文献［11］的实验数据与有限元磨损模型的计算结果对比图.从图中可以看出，在载荷为185 N的条件下，实验结果和有限元模型计算的结果非常接近.

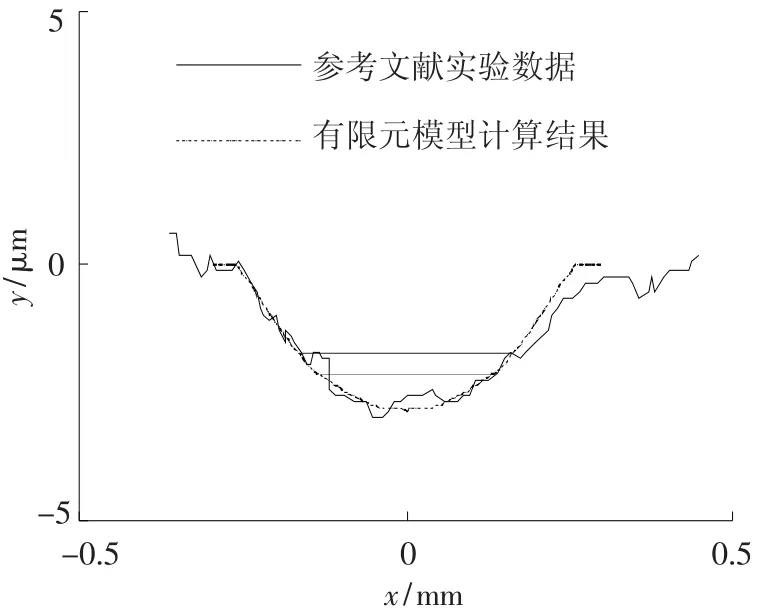
图6 参考文献实验数据与本文的有限元磨损模型计算结果对比(载荷:185 N，磨损次数:18 000次)

图7是文献［11］的实验所测得的摩擦系数.从图中可以看出，在磨损过程中，摩擦系数并不是一个恒定的值，而是由初期一个较小的值逐渐增大并最终在一个小的范围内波动.因此，本文就不同的摩擦系数对磨损的影响进行了讨论.

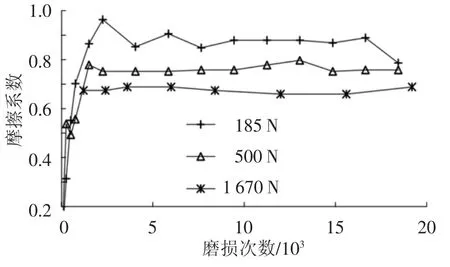
图7 摩擦系数随磨损次数的变化(往复运动幅值:25 μm，频率:20 Hz)

图8是有限元预测模型在载荷为500 N，往复运动幅值为25 μm的条件下，在不同的摩擦系数下磨损5 000次后圆柱的表面轮廓.从图中可以看出，随着摩擦系数的增大，磨损量呈现出减小的趋势.根据本文的Archard模型，磨损量是接触压力和滑移量的函数.从图9中可以看出，摩擦系数对接触压力的影响并不是很明显，但放大后仍可发现接触压力随摩擦系数的增大而减小.而随着摩擦系数增大，滑移量亦随之减小(如图10所示)，这都是导致磨损量随摩擦系数增大而减小的原因.从图10还可以看出，在500 N的载荷下的滑移均为整体滑移，并且滑移量均小于实际的滑动距离.越靠近中心区域，滑移量越小.

在磨损的过程中，往往同时也伴随着疲劳.在疲劳的产生过程中，正应力和剪应力的变化是非常重要的现象［12］.图11是有限元预测模型在载荷为500 N，往复运动幅值为25 μm的条件下，在不同的摩擦系数下磨损5 000次后的x方向正应力和剪应力分布.从图中可以看出，不同摩擦系数下的x方向正应力和剪应力均在磨损边界处出现峰值，并且随着摩擦系数的增大，这个峰值也逐渐增大.因此，在其他条件相同的情况下，较大的摩擦系数会比较容易导致疲劳的发生.

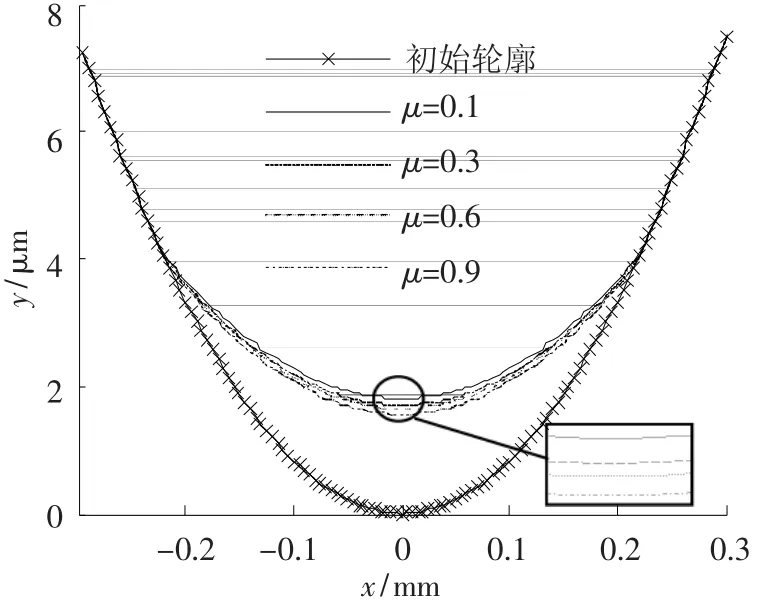
图8 不同的摩擦系数下磨损5 000次后圆柱的表面轮廓(载荷:500 N，幅值:25 μm)

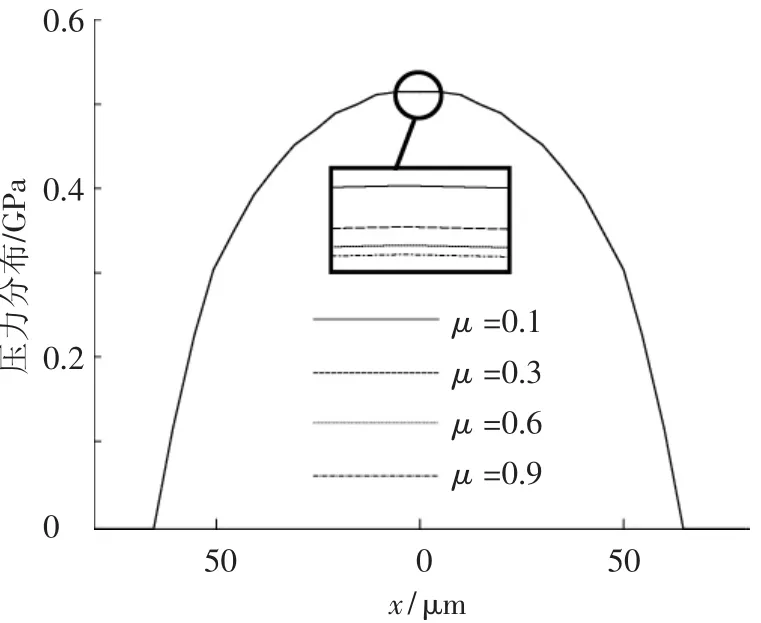
图9 不同摩擦系数的压力分布(载荷:500 N)

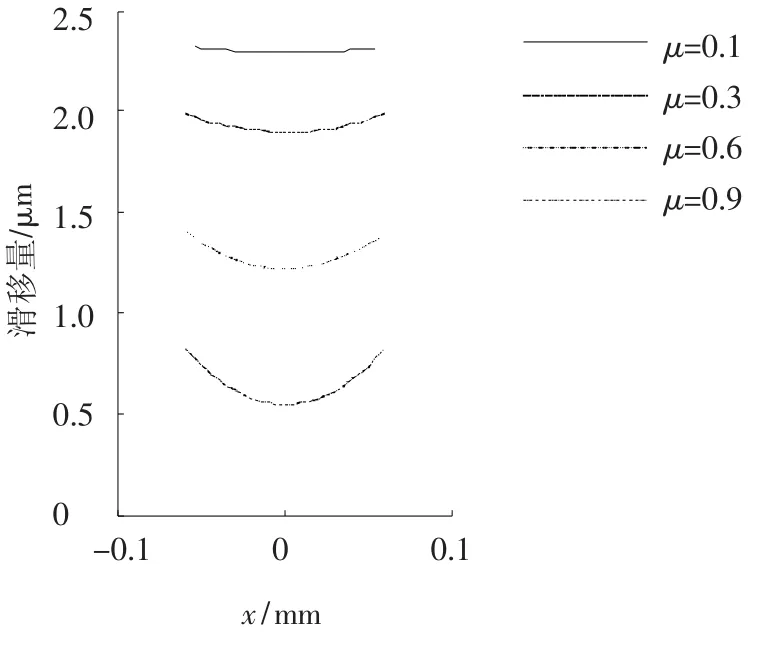
图10 不同摩擦系数下移动2.5 μm后的滑移量(载荷:500 N)

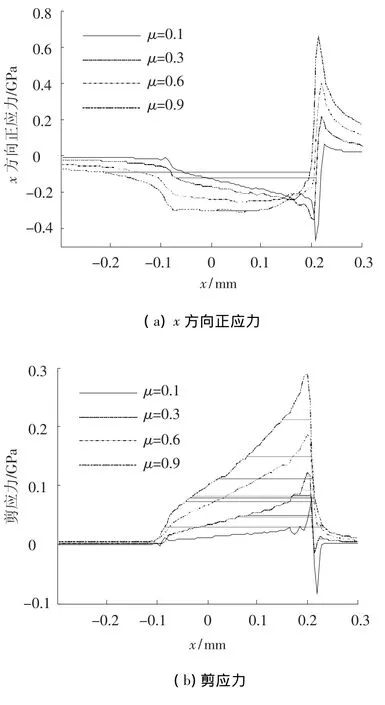
图11 不同摩擦系数下磨损5 000次后应力分布(载荷:500 N，幅值:25 μm)

3 结论

1)利用有限元的方法，将连续的磨损过程离散化，选取适当的磨损放大因子来缩短计算时间，采用有限元分析软件来进行磨损过程的仿真，可以为实际工程应用提供一种摩擦磨损分析工具.

2)由仿真计算结果发现，较大的摩擦系数会降低接触面滑移量和接触压力，从而降低磨损量.较大的摩擦系数同时也会导致接触区域正应力和剪应力上升，进而加速接触疲劳的产生.

［1］温诗铸，黄平.摩擦学原理［M］.第2版.北京:清华大学出版社，2002:301-302.

［2］蒋翔俊，张优云，袁淑霞.燃机端面齿微动磨损分析及数值仿真［J］.哈尔滨工业大学学报，2011，43(3):75-79.

［3］汪选国.销盘滑动磨损试验的仿真方法研究［D］.武汉:武汉理工大学能源与动力工程学院，2009:1-7.

［4］冯伟.滑动磨损试验的有限元法数字仿真研究［D］.武汉:武汉理工大学能源与动力工程学院，2005:25-33.

［5］SFANTOS G K，ALIABADI M H.Wear simulation using an incremental sliding boundary element method［J］.Wear，2006，260(9/10):1119-1128.

［6］PODRA P，ANDERSSON S.Finite element analysis wear simulation of a conical spinning contact considering surface topography［J］.Wear，1999，224(1):13-21.

［7］REZAEI A，VAN PAEPEGEM W，DE BAETS P，et al.Adaptive finite element simulation of wear evolution in radial sliding bearings［J］.Wear，2012，196(1/2):660-671.

［8］CRUZADO A，URCHEGUI MA，GOMEZ X.Finite element modeling and experimental validation of fretting wear scars in thin steel wires［J］.Wear，2012，289:26-38.

［9］宿月文，陈渭，朱爱斌，等.滑动磨损过程有限元分析及销磨损预测［J］.中国机械工程，2009，20(13):1573-1581.

［10］MOHD TOBI A L，DING J，BANDAK G，et al.A study on the interaction between fretting wear and cyclic plasticity for Ti-6Al-4V［J］.Wear，2009，267(1/2/3/4):270-282.

［11］MCCOLL IR，DING J，LEEN SB.Finite element simulation and experimental validation of fretting wear［J］.Wear，2004，256(11/12):1114-1127.

［12］DING J，LEEN S B，MCCOLL I R.The effect of slip regime on fretting wear-induced stress evolution［J］.International Journal of Fatigue，2004，26(5):521-531.