间歇热流下管式吸热器温度场及热应力场分析

王富强，帅 永，谈和平，林日亿

(1.中国石油大学(华东)储运与建筑工程学院，266580山东青岛;2.哈尔滨工业大学能源科学与工程学院，150001哈尔滨)

太阳能热利用是可再生能源发展的有效途径之一.目前国际上太阳能热发电技术主要有槽式、塔式和碟式［1］3种形式，其中塔式和碟式太阳能热发电技术仍处于试验和示范阶段，而槽式太阳能热发电技术已成为成熟的商业化技术.槽式聚光器利用抛物线的几何光学特性将低辐射热流密度的太阳光汇聚后，形成高汇聚热流.安置在槽式聚光器焦平面处的管式吸热器吸收高汇聚热流并通过导热、对流等耦合换热的方式将高汇聚热流转换为热能.

由于太阳能一方面受到昼夜、季节和地理纬度等规律性因素的影响，另一方面又受到晴朗、阴云和雨雪天气等随机因素的制约，因而太阳能的热利用具有显著的间断性和不均匀性，吸热器容易承受高的热应力，引发玻璃管罩的破裂、管式吸热器的弯曲并最终失效［2］，如:墨西哥国立大学太阳能热利用电站在运行和试验中，多次发生不锈钢管式吸热器的大弯曲变形并引发玻璃罩破裂的事故［3～5］.

管式吸热器热应力场的研究可以为提高吸热器的可靠性提供理论指导，Kim等［6］采用有限体积与有限元联合计算法对管式吸热器的热变形进行了分析;王志峰等［7］采用商业软件Ansys对管式吸热器密封节的残余热应力进行了计算;王富强等［8］采用顺序解耦的计算方法对管式吸热器的热应变进行分析，指出采用偏心管式吸热器替代同心管式吸热器可以有效地降低吸热器热应变.

在对吸热器的温度场及热应力场分析时，目前大多数学者都假定入射太阳能热流与吸热器表面呈垂直关系［9～12］，没有考虑到太阳能热流入射方向与吸热器表面之间夹角关系.本文采用命令流编程方式，在对管式吸热器进行网格划分之后，计算吸热器外表面每一单元网格面的法线方向与太阳能热流入射方向之间的余弦关系与汇聚热流的乘积，并将其作为温度场分析求解的边界条件.

1 几何模型及模拟方法

1.1 几何模型

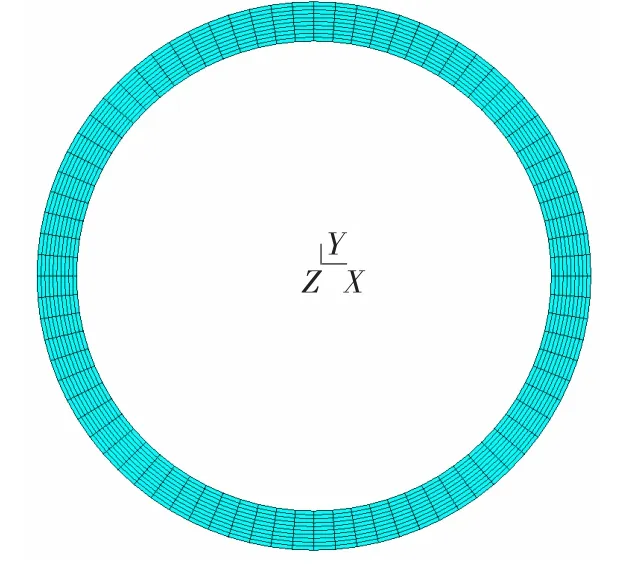
图1 管式吸热器网格划分

1.2 计算方法

与 Submodeling方法相比，Coupled-field element方法在温度场和应力场分析过程可以采用相同的网格并同时对温度场和应力场方程矩阵进行计算求解.因此，Coupled-field element方法求解过程更简便，更适于含有函数边界条件下的命令流编程分析.在热应力场分析过程中没有采用任何的外部约束，因此，管式吸热器的热应力是由于吸热器管壁上不均匀温度分布和吸热器自身几何形状的约束所产生［13］.

为了验证计算方法的可靠性，在采用相同的几何模型尺寸及边界条件下，将本文计算得到的径向应力及切向应力沿长度变化曲线与文献［14］进行了对比验证.验证算例为陶瓷管式换热器在管壁内侧施加均匀对流换热系数及非均匀对流换热系数两种边界条件下的热应力场分析，其中管壁外侧施加均匀热流密度(800 W/m2)的边界条件.由图2可知，本文计算得到的径向应力及切向应力沿长度方向变化曲线与文献［14］吻合良好.

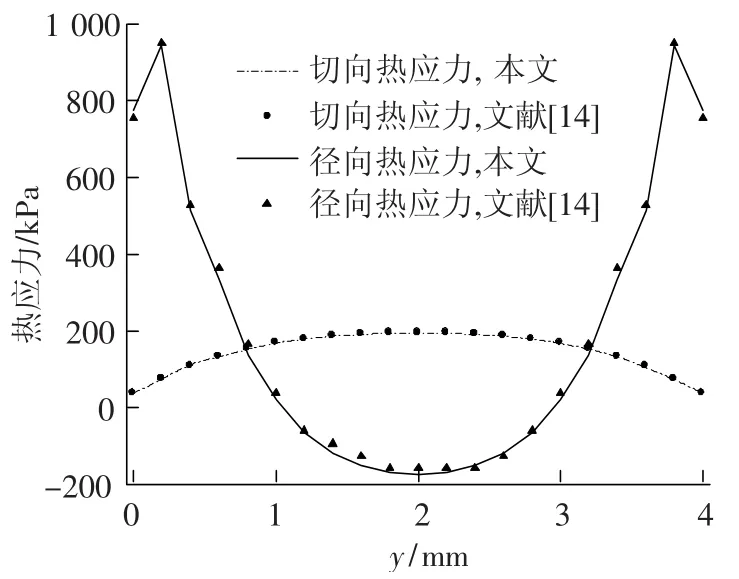
图2 本文计算结果与文献［14］的对比验证

1.3 边界条件

在数值模拟过程中，假设管壁材料物性不随温度变化，分析不锈钢管式吸热器的温度场以及热应力场的分布.

1.3.1 吸热器内壁面

由于在进行热应力场分析过程中，管式吸热器内部流体不具有刚度矩阵，无法进行热应力场分析，因此采用对管式吸热器内壁面施加一恒定对流换热系数方法进行分析.管式吸热器内壁面施加边界条件如下:

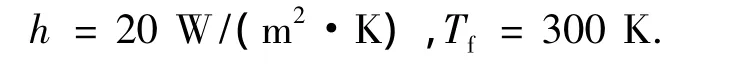
1.3.2 吸热器外壁面

考虑到太阳能热流入射方向与吸热器表面之间夹角关系，每一个单元网格上的太阳能热流入射方向与单元网格法线方向之间角度变化关系如图3所示.

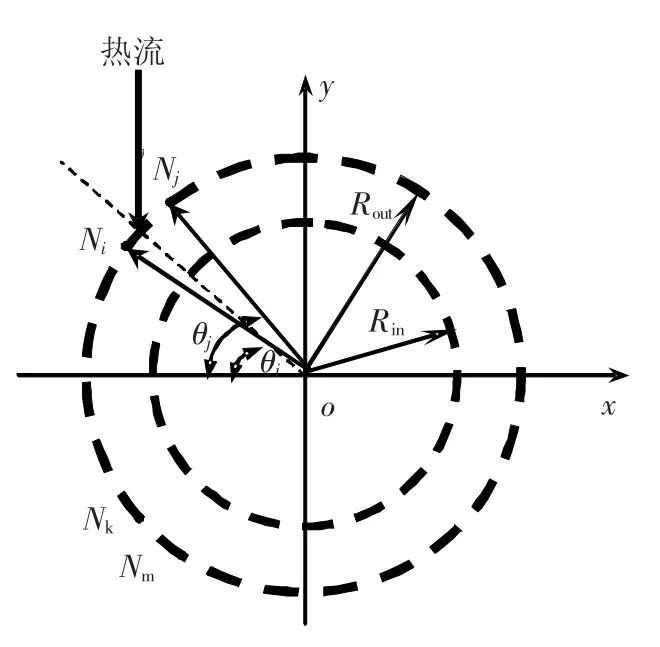
图3 单元网格上热流入射方向与网格法线之间夹角关系

由文献［6］可知，吸热器外壁面上每一个单元网格面受到热流密度为

A：通过这几年的实践，我们认为，VOCs治理应该从源头入手，对过程进行控制，并辅以末端治理。源头，是我们治理的重点，目前我们使用的是无醇润版液，因为不用酒精了，整个生产车间的空气质量大大改善，几乎闻不到刺鼻的气味。过程控制，主要是做好各项管理，使VOCs排放源处于管控之中。末端治理，即VOCs的收集系统，这也是非常关键的一环。

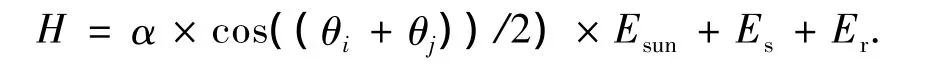
其中，θi为网格节点i与水平面之间的夹角，Esun为太阳辐照度(Esun=1000W/m2)，Es和Er分别为大气中的散射辐射和反射辐射.由于大气中散射辐射和反射辐射相对较小且影响因素很多［15］，本文计算中忽略不计.α为吸热器表面吸收系数.由于管式吸热器的表面具有高吸收率涂层(可高达0.97)及玻璃罩抑制辐射损失的作用［15］，本文选择理想性吸收表面进行计算，即α=1.0.

考虑到管式吸热器受到间歇太阳能热流的特点，对管式吸热器外壁面下表面施加一移动热源.移动热源的大小也同样考虑到每一个单元网格上的太阳能热流入射方向与单元网格法线方向之间角度变化关系，移动热源的大小沿管壁圆周方向随着夹角变化而不断变化.移动热源位置沿吸热器长度方向随时间步长不断变化来模拟间歇热流的影响，如由阴天突变为晴天、日升日落等.由文献［6］可知:

移动热源为

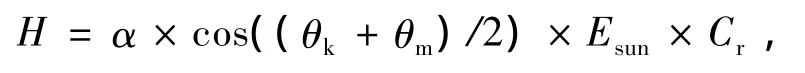
其中Cr为几何汇聚比;

移动热源位置为

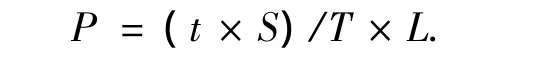
其中:为t为时间步长，t=0.1s;S为时间步数;T为总的计算时间，T=t×St;St为总的计算时间步数.由文献［13-14］可知，热应力产生的主要原因是温度场的突变，均匀、线性变化温度场均不会引起热应力.因此，本文选用总的计算时间为10s来模拟间歇热流的作用，即St=100.

1.3.3 吸热器端面

为了使温度场变化对热应力场的影响这一研究更清晰，在热应力场分析过程中管式吸热器两端面没有采用任何的外部约束.

2 计算结果与分析

2.1 不锈钢管式吸热器的温度场分布

图4为不同时间步下不锈钢管式吸热器外壁面在y=0位置处温度场沿长度方向变化曲线.由于移动热源的加载是随时间沿管式吸热器长度方向不断前进的，因此在所有的时间步下，最高温度出现在z=0位置处，沿着长度方向温度不断递减.随着时间的推移，吸热器的最高温度不断上升，在时间步s=100时，不锈钢管式吸热器最高温度已经达到了572K.这是由于随着时间的增长，受到高汇聚比太阳能热流的面积不断增大.由文献［13］可知，热应力场与温度的二阶导数呈函数关系，因此本文将温度场沿长度方向进行二次求导来揭示热应力场与温度场的变化关系.

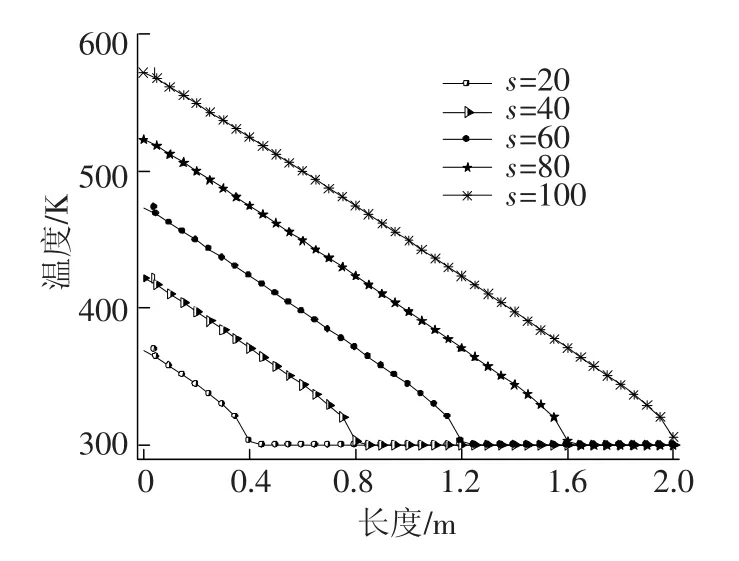
图4 不同时间步下管式吸热器温度场沿长度变化

图5所示为不同时间步下不锈钢管式吸热器外壁面在y=0位置处温度场的二阶导数沿长度方向变化曲线.

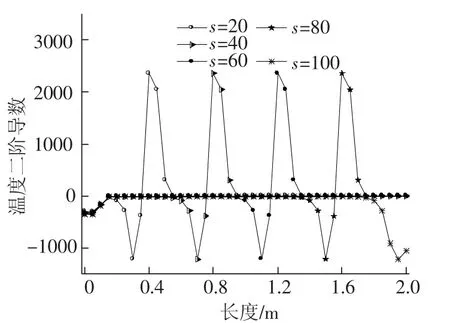
图5 不同时间步下管式吸热器温度二阶导数沿长度变化

由图5可知，不同时间步下温度二阶导数曲线形状基本一致，不同时间步下的温度二阶导数曲线的波峰与波谷的数值也相差很小.不同时间步下温度二阶导数曲线的波峰与波谷值出现的位置随着时间步增长而沿着管式吸热器长度方向推移，但是温度二阶导数的波峰与波谷值并不是出现在移动热源加载位置边界处，而是在移动热源加载位置边界稍靠前位置处.

2.2 不锈钢管式吸热器的应力场分布

图6为不同时间步下不锈钢管式吸热器外壁面在y=0位置处轴向热应力场沿长度方向变化曲线.由图6可知，不同时间步下轴向应力沿管式吸热器长度方向变化趋势是一致的:轴向应力沿着管式吸热器长度方向首先是不断下降，一直达到曲线的波谷值;然后轴向应力沿着长度的方向增加呈现出线性增长到达轴向应力曲线的第二拐点处，此后轴向应力急速增长并趋近于零.对比轴向应力与温度二阶导数沿管式吸热器长度方向变化曲线可以发现，在轴向应力曲线的拐点处均是温度二阶导数曲线拐点处.以时间步S=20为例:温度二阶导数曲线在L=0.18 m处出现了曲线的拐点，温度二阶导数数值由负值变为零，而轴向应力曲线在L=0.18 m处也出现了曲线的拐点，此拐点为轴向应力曲线波谷值;温度二阶导数曲线在L=0.25 m处出现了曲线的拐点，而轴向应力曲线在L=0.25 m处也出现了曲线的拐点，经历此拐点后，轴向应力曲线继续上升并趋近于零;温度二阶导数曲线在L=0.42 m处出现了曲线的拐点，即为温度二阶导数曲线的峰值，而轴向应力曲线在L=0.42 m处也出现了曲线的第3个拐点，在此拐点处，轴向应力曲线数值变为0.

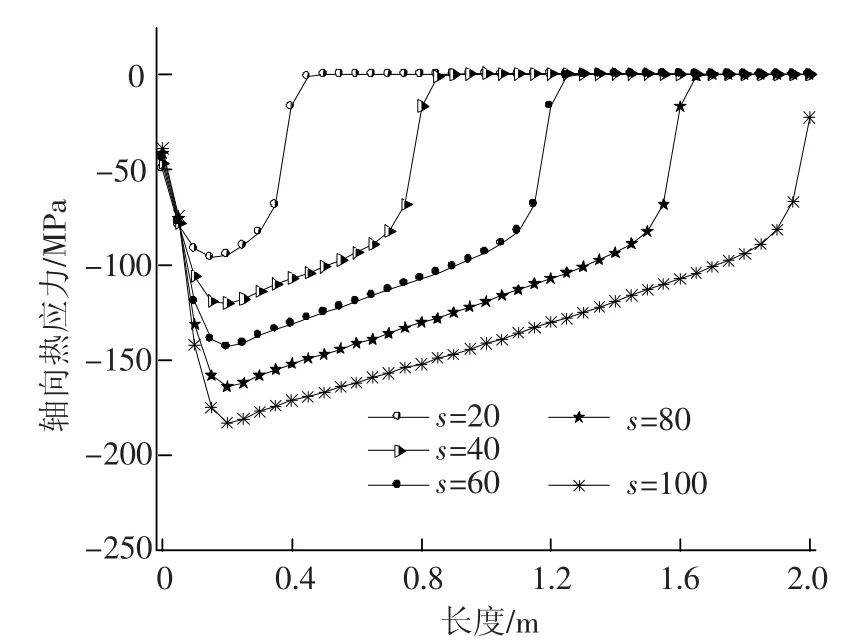
图6 不同时间步下管式吸热器轴向应力沿长度变化

对比图5与图6可知，虽然不同时间步下的温度二阶导数曲线的波峰波谷数值大小相差不大，但是不同时间步下的轴向应力的大小却有着比较大的变化.这是由于不同时间步下，温度二阶导数的拐点出现位置不同而引起的.由弹性力学理论可知，在不考虑材料物性随温度场变化时，对管式吸热器不同位置施加相同的载荷而引起管式吸热器变形大小也不相同，因此产生的应力的数值大小也不相同，因此发生了不同时间步下相同位置的轴向应力值变化较大的现象.

图7为不同时间步下不锈钢管式吸热器外壁面下表面在y=0位置处径向热应力场沿长度方向变化曲线.不同时间步下的径向应力数值最大值均出现在z=0的端面处，径向应力表现为压应力.这是由于在z=0的端面处出现温度峰值，且在此端面处温度沿半径方向变化最为剧烈.不同时间步下径向应力沿管式吸热器长度方向变化曲线形状基本一致.除z=0的端面处外，不同时间步下的径向应力变化曲线的波峰与波谷的数值也相差很小.同温度二阶导数沿长度方向变化曲线一样，不同时间步下径向应力变化曲线的波峰与波谷值出现的位置随着时间步增长而沿着管式吸热器长度方向推移.与轴向应力相比，相同时间步下的最大径向应力仅为轴向应力的1/10左右.

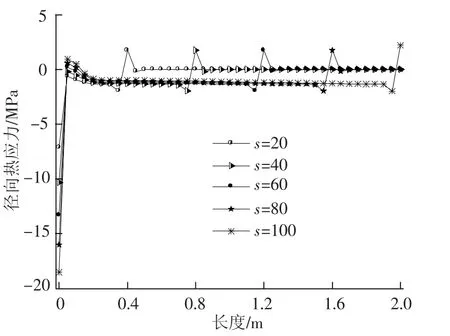
图7 不同时间步下管式吸热器径向应力沿长度变化

图8为不同时间步下不锈钢管式吸热器外壁面在y=0位置处切向热应力场沿长度方向变化曲线.同径向应力沿长度方向变化曲线一样，切向应力最大值均出现在z=0的端面处且均表现为压应力.切向应力沿长度变化曲线的变化趋势与径向应力变化趋势基本上是一致的.对比切向应力与温度二阶导数沿管式吸热器长度方向变化曲线可以发现，切向应力曲线发生拐点处均是温度二阶导数曲线拐点发生处.

图9为不同时间步下不锈钢管式吸热器外壁面下表面在y=0位置处等效应力Von-Mises热应力场沿长度方向变化曲线.不同时间步下等效应力Von-Mises热应力沿管式吸热器长度方向变化趋势是一致的.由等效应力Von-Mises应力理论可知［13-14］，轴向应力和切向应力对 Von-Mises热应力场影响最大，径向应力影响最小.等效应力Von-Mises热应力沿长度方向变化曲线的拐点处均是温度二阶导数沿长度方向变化曲线的拐点发生处，这与文献［13-14］研究得到结论相同.

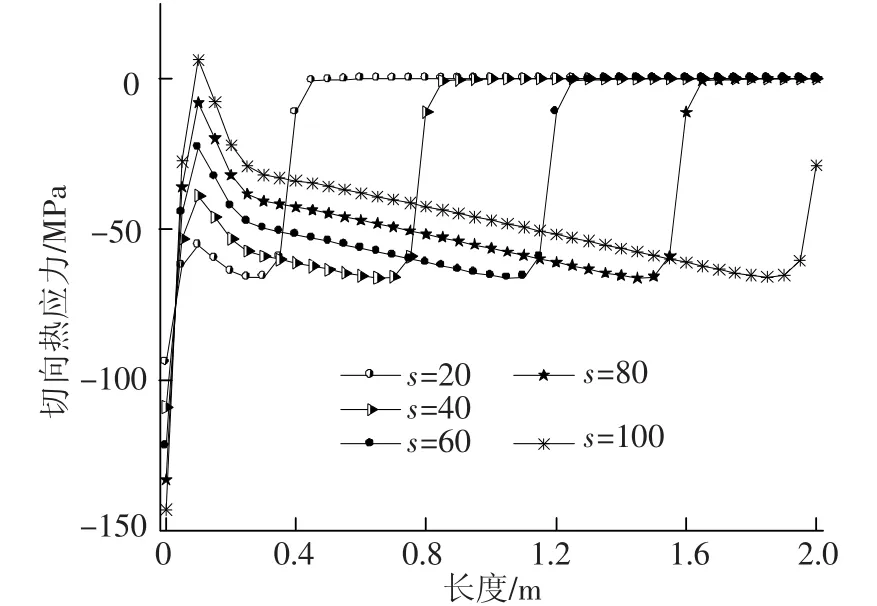
图8 不同时间步下管式吸热器切向应力沿长度变化

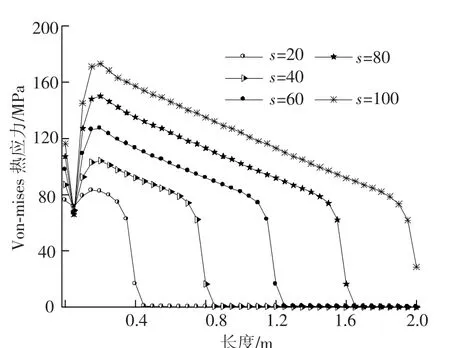
图9 不同时间步下管式吸热器等效应力沿长度方向变化

3 结论

1)本文采用命令流编程方式，计算吸热器外表面每一单元网格面的法线方向与太阳能热流入射方向之间的余弦关系，并以此余弦关系作为温度场分析求解的边界条件.采用 Coupled-field element方法对管式吸热器的温度场和应力场进行了耦合求解计算.

2)研究了管式吸热器在不均匀热流密度以及间歇太阳能热流边界条件下的温度场分布以及热应力场分布.

3)研究了温度场沿长度方向二阶导数变化规律，发现热应力曲线拐点处均是温度二阶导数曲线拐点发生处.

［1］方嘉宾，魏进家，董训伟，等.腔式太阳能吸热器热性能的模拟计算［J］.工程热物理学报，2009，30(3):428－432.

［2］LATA J M，RODRIGUEZ M A，de LARA M A.High flux central receivers of molten salts for the new generation of commercial stand-alone solar power plants［J］.ASME Journal of Solar Energy Engineering，2008，130(2):0210021－0210025.

［3］ ALMANZA R F，LENTZ A，JIMENEZ G.Receiver behavior in direct steam generation with parabolic toughs［J］.Solar Energy，1997，61:275 －278.

［4］ ALMANZA R F，FLORES V C，LENTZ A，et al.Compound wall receiver for DSG in parabolic troughs［C］//Proceedings of the 10th international symposium of solar thermal.Sydney:Solar PACES，2002:131 -135.

［5］FLORES V C，ALMANZA R F.Behavior of compound wall copper-steel receiver with stratified two-phase flow regimen in transient states when solar irradiance is arriving on one side of receiver［J］.Solar Energy，2004，76:195-198.

［6］ KIM D C，CHOI Y D.Analysis of conduction-natural convection conjugate heat transfer in the gap between concentric cylinders undersolarirradiation ［J］.International Journal of Thermal Science，2009，48(6):1247-1258.

［7］LEI Dongqiang，WANG Zhifeng，LI Jian.The analysis of residual stress in glass-to-metal seals for solar receiver tube［J］.Materials and Design，2010，31(4):1813 -1820.

［8］ WANG Fuqiang，SHUAI Yong，YUAN Yuan，et al.Thermal stress analysis of eccentric tube receiver using concentrated solar radiation［J］.Solar Energy，2010，85(10):1809-1815.

［9］刘斌，吴玉庭，杨征，等.螺旋盘管腔式熔盐太阳能吸热器的分析优化和研制［J］.工程热物理学报，2009，30(6):995－998.

［10］KUMAR N S，REDDY K S.Comparison of receivers for solar dish collector system ［J］.Energy Conversion and Management，2008，49:812 －819.

［11］YAPICI H S，ALBAYRAK B.Numerical solutions of conjugate heat transfer and thermal stresses in a circular pipe externally heated with concentrated solar irradiation heat flux ［J］.Energy Conversion and Management，2004，45:927 －937.

［12］KUMAR N S，REDDY K S.Thermal analysis of solar parabolic collector with porous disc receiver ［J］.Applied Energy，2009，86:1804 -1812.

［13］IFRAN M A，CHAPMAN W C.Thermal stresses in radiant tubes due to axial，circumferential and radial temperature distributions ［J］.Applied Thermal Engineering，2009，29:1913 -1920.

［14］ISLAMOGLU Y S.Finite element model for thermal analysis of ceramic heat exchanger tube under axial concentrated solar irradiation convective heat transfer coefficient［J］.Materials and Design，2004，25:479 －482.

［15］何梓年.太阳能热利用［M］.合肥:中国科学技术大学出版社，2009:31－98.