附加几何条件所得到的平面时差定位解析方程

郁 涛

(上海微波设备研究所，上海201802)

0 引言

多站时差定位系统通过处理3个或更多测量站所采集到的信号到达时间测量数据对辐射源进行定位，一旦获得了到达时间差(Time Difference of Arrival，TDOA)的测量值，就可以得到辐射源到各测量站的距离差，由此即可构成一组关于辐射源位置的双曲线(面)方程组，求解该双曲方程组就可以得到辐射源的坐标位置。但求由时差所确定的双曲线或双曲面交点的过程是非线性的，没有解析解。目前，常见的用于时差定位的算法大多还停留在理论阶段［1］，很少应用在实际工程中。同时，传统求解非线性方程组的方法是建立在迭代运算和线性化的基础上［2－5］，需要对辐射源位置进行初始估计，所以这种求解方法的精度较强地依赖于初始位置估计是否准确。当初始估计较差时，不一定能得到收敛解，同时这种估计方法的运算量也是很大的。此外，在定位解算过程中，由于双曲线(面)交叉有时会出现定位模糊，寻求去除定位模糊的方法也是时差定位处理中需要解决的问题。本文的初步研究结果表明，对于平面3站时差定位问题，在时差测量的基础上，只要充分利用现有的平面几何关系即可获得解析解。

1 基于几何条件的平面解析方法

对任意布站的平面3站定位系统，其几何模型如图1所示，设S1为主站，其余两站S2和S3为副站。近似忽略远距目标的高度，假定目标T(x，y)亦位于二维平面内。图1中在径向距离r1和基线d1之间的夹角β是未知的目标方位角，而基线长度di和站间基线的夹角β0，则是在布站的同时都可被确定的值。

基于时差测量，有如下的程差定位方程:

式中，Δri为副站与主站之间的程差;vc为光速;Δt(i+1)1为主副站之间的时差。

另由余弦定理可列出如下两个三角定位方程:

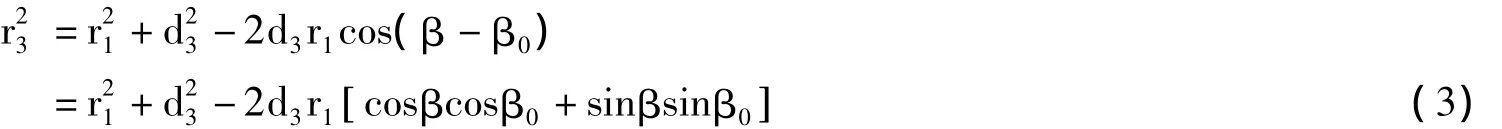
从式2中可解出基于径向距离与基线长度测量的目标方位表示式:

式4代入式3:

图1 平面3站时差定位阵列的示意图

从程差关系式:ri+1=r1+Δri，得到:

同时代入式5:

将式8变形处理后有:

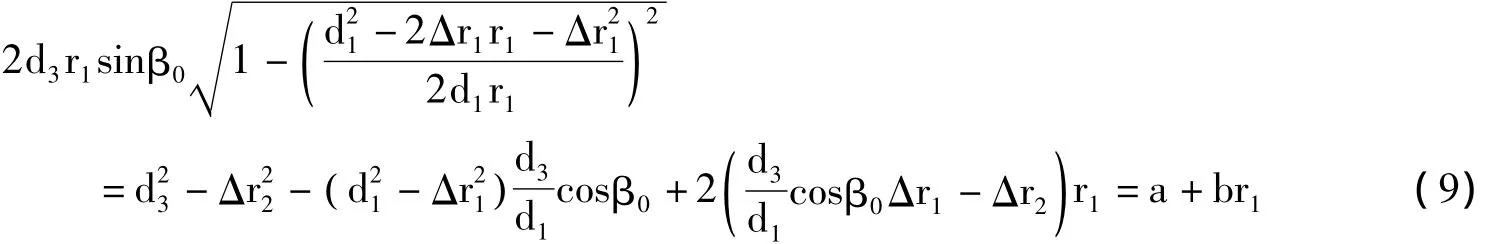
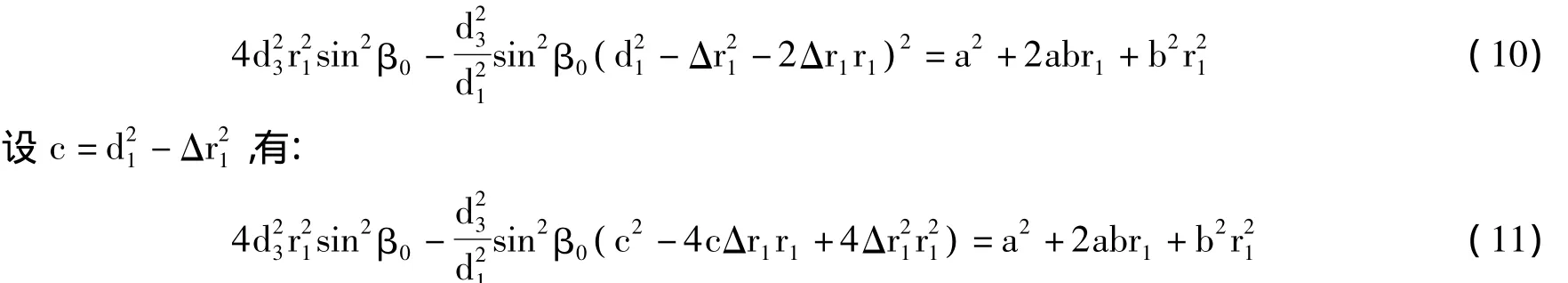
展开后有:

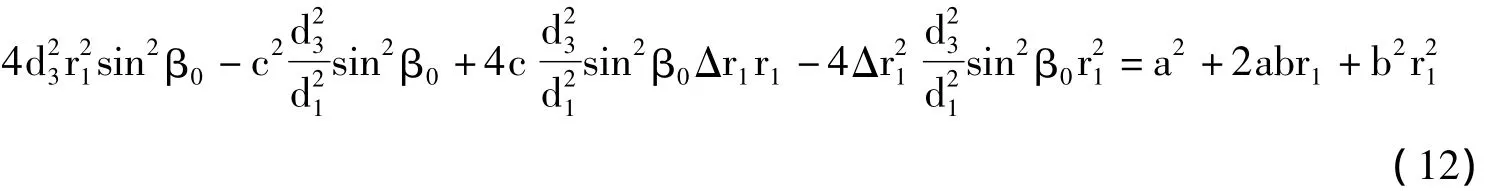
最后得到一个一元二次方程:

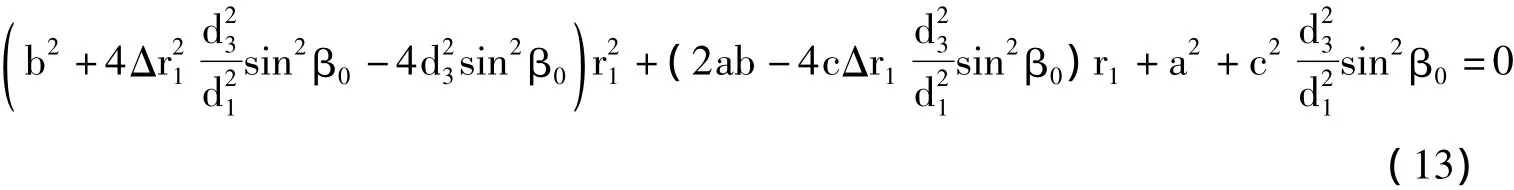
式13可整理变形为:

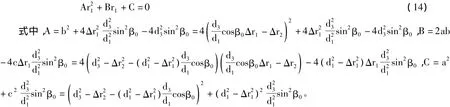
一旦当角度β0趋于零，即3站为直线排列时，式14将退化为:

即为a+br1=0，可得到:

这和3站直线排阵时，直接从时差(程差)方程所得出的结果是完全一致的，此验证结果说明利用附加的几何条件，无需进行复杂的非线性运算，即可由时差方程得到解析结果。

2 模拟验证

模拟验证主要是考核计算公式的准确性，通过将理论给定值和由式14的一元二次方程的求根公式，得:

所得到的结果和理论值相比较，即得到计算式的相对计算误差:

式中，下标a表示公式的测算解。

不同夹角β0时的相对计算误差曲线如图2所示。在的区间内，正根使用范围约对应着的区域，而负根则对应着的区间。计算时所使用的参数为计算发现，如两基线的长度不等，则正负根的使用区间将会发生变动，增大d2将则扩大负根的使用范围。但如d1＞d2，则方程将出现无解。

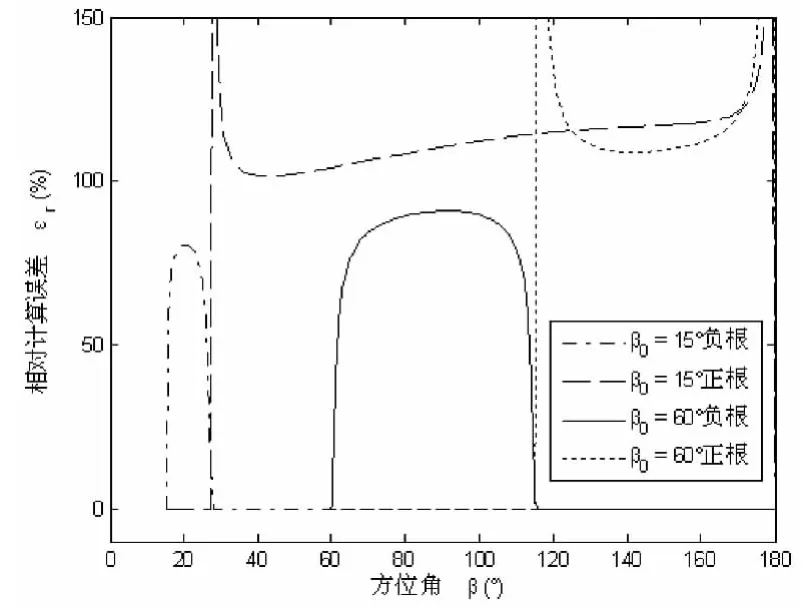
图2 不同方位角β0时的相对计算误差曲线

3 结束语

对于时差定位系统，目标的定位误差是与目标相对于测量站的几何关系密切相关的［6，7］，在时差测量误差及测量站站址误差等误差因素一定的情况下，对测量站进行布站优化，是提高定位精度的有效手段。本文所给出的平面时差定位解析方程，将有助于进一步深入研究及优化多站时差定位系统的观测站构形问题，且对于提高时差定位系统的实际工作效能具有十分积极的意义。

［1］James J Caffery，Gordon L Stuber.Overview of Radio Location in CDMA Cellular Systems［J］.IEEE Communication Magazine，1998，36(4):38 －45.

［2］潘琴格.无源系统测向及时差频差联合定位方法研究［D］.西安:西安电子科技大学，2005.

［3］张正明.辐射源无源定位研究［D］.西安:西安电子科技大学，2000.

［4］刘刚.分布式多站无源时差定位系统研究［D］.西安:西安电子科技大学，2006.

［5］任连峻.时间测量及无源多站定位方法研究［D］.哈尔滨:哈尔滨工业大学，2006.

［6］钱镱，陆明泉，冯振明.基于TDOA原理的地面定位系统中HDOP的研究［J］.电讯技术，2005，45(4):135－138.

［7］王成，李少洪，黄槐.测时差定位系统定位精度分析与最优布站［J］.火控雷达技术，2003，32(1):1－6.