基于遗传算法的车辆路径问题ExtendSim仿真与优化

詹长书，陈勇汛（东北林业大学 交通学院，黑龙江 哈尔滨 150040）

ZHAN Chang-shu,CHEN Yong-xun (Northeast Forestry University Traffic College,Harbin 150040,China)

我国国家标准《物流术语》 （GB/T 18354-2006）中，给物流下的定义是：“物流是指物品从供应地向接收地的实物流动过程。根据实际需要，将运输、存储、装卸、搬运、包装、流通加工、配送、信息管理等基本功能实施有机结合。”物流有多方面的功能，而运输和储存保管则是其主要功能。在整个物流活动过程中，运输是其中各项子活动的核心活动，它是第三利润源的主要的源泉[1]。

日本在20世纪70年代就对物流有深刻的认识了，日本早稻田大学的西泽修教授在其著作中把物流称作不为人知的利润源泉，他认为，物流能为企业创造价值，是企业的利润源泉。石油危机后这一观点得到证实，物流也因而在企业管理中得到更加重视。目前我国生产型企业的物流成本占到总成本的20%～30%，而发达国家的则为10%左右[2]。因此，为了降低企业经营成本，获得更多的利润，必须尽量降低物流成本的比重，这对于国民经济的更好发展具有十分重要的作用。

在商品经济社会中，人们的生活质量与商品消费息息相关，而商品的价格直接影响人们的生活水平，如果商品价格不合理，超出人们普遍的可接受范围，那么人们的生活幸福度将会大大降低。而商品价格的构成部分除了有生产成本，还有更重要的一部分是物流成本，并且物流成本中的运输费又占了较大的比重。商品运输需要耗费大量的能源动力，消耗越多，花费成本越高，如果运输组织的不合理，就会加大运输成本，因而抬高物流成本，商品价格也因而升高，结果是不仅降低企业的利润，也间接提高人们的生活成本。

所以，运输问题是物流领域中值得研究的关键问题。其中车辆路径问题（Vehicle Routing Problems，VRP）是运输问题中的一个热点问题。该问题是指：在物资流通过程中，每个需求点的位置和需求量已知，供方如何调度车辆和安排行车路径向需方供应物资，使得在满足需方需要的同时也达到某些关键目标（如车辆数尽量少、花费时间尽量少、费用最少、路程最短等）。

学者们很早就开始对车辆路径问题进行了研究，积累了丰富的研究成果。在20世纪50年代末，车辆路径问题首先被G.Dantzig和J.Ramser[3]提出，两位学者根据如何运送汽油到加油站这个现实中的问题，利用数学方法对其建立模型，并得出求解算法。在1964年，Clark和Wright这两位学者研究了G.Dantzig和J.Ramser的方法后，认为后者的方法有改进的空间，并最后提出了Clark-Wright节约算法（即C-W算法）。从此VRP成为运筹学领域的研究热点。五年后，Christofides与Eilon又想出新的方法，他们应用2-opt和3-opt处理VRP，取得较好的效果。到1981年，Fisher、Jaikumar和Gullen、Ratliff、Jarvis提出不同的研究方法。前者主要利用数学规划，来对VRP进行最优化处理，后者则是运用人机互动的启发式方法处理VRP。到90年代，学者们开始利用人工智能构造大量的启发式算法来解决VRP，如禁忌搜索发、模拟退火法、遗传算法等。首先采用遗传算法（Genetic Algorithm，GA）的学者是Holland[4]，他利用遗传算法中的编码方法处理了VRP。在这几种人工智能方法中，遗传算法能较好地逼近最优解的同时具有较高的运算速度和效率，具有很好的发展前途。

1 VRP数学模型及遗传算法

1.1 VRP的基本数学模型

VRP的一般描述[5]：

（1）车辆的载重量大于等于配送路径上总的需求量；

（2）任一配送路径的长度小于等于车辆在一次配送任务中的最大行驶距离；

（3）每个需求点的需求都只能被同一辆送货车满足；

（4）设定每辆车都是从中心出发开展配送任务，任务完成后再重新回到中心。

将一个配送中心编号设为0，该配送中心拥有车k辆，车辆数m，车的额定载重量为q，该中心面向L个客户，第i个客户需求量为gi，且gi≤q（i=1,2,…,L），VRP的基本模型如下：

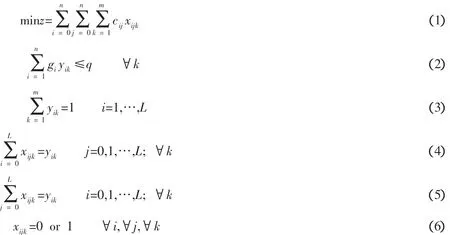
以上式（1）中，cij表示由点i到点j的运输成本，该函数为最小运输成本目标函数；（2）为车容量的约束；（3）表示每个客户仅有一辆车服务；（4）、（5）表示到达和离开某一客户仅有一辆车。xijk和yki为变量，定义为：

1.2 遗传算法

本文中的仿真软件ExtendSim拥有一个自带遗传算法的优化模块。遗传算法在处理车辆优化调度问题时，有以下几个步骤：

（1）确定染色体的编码和初始群体

对可行路线编码，如长度为1+m的染色体编为：

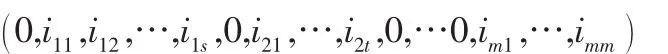
i代表着每一项运输任务，此染色体可理解为车辆从配送中心0出发，完成i11,i12,…,i1s后返回配送中心0，形成子路径1；然后又从0出发，完成i21,…,i2t后返回0，形成路径2，如此反复直至完成所有的任务。这个过程中，行走路径不断改变，使得函数目标也改变，这样的遗传迭代就能让函数目标最小，也即趋向于最佳路径。

（2）确定目标函数

根据所研究的具体问题，数学模型的目标函数可以表示相应问题（如运费最少问题、车辆数最少问题、路径最短问题、运输时间最少问题等）的最优解方程。

（3）约束的处理

遗传算法中各个染色体对应的解在群体中是占有一定比重的，在遗传算法迭代运算进程中，如果某个染色体的解不符合约束条件，则会受到遗传算法的惩罚机制的惩罚，使得其在群体中所占比重越来越小，而相反，可行解则越来越大，通过这样的一个机制最终可以得出最优解。

（4）遗传算子

遗传算子一般包括复制、交叉、变异。复制的目的是保留优良个体，提高全局收敛性和效率；交叉的作用是组合新个体，降低对有效模式的破坏概论；变异的目的，是为了减少基因的缺失和不成熟收敛对结果的影响。

（5）确定最终方案

经过上述遗传过程后，最终产生性能最优的染色体串。

2 仿真优化方法在VRP上的运用

对VRP的研究，大多停留在理论层面上，这些研究是通过分析问题，运用运筹学知识，用各种数学符号将问题抽象为一系列公式，形成能解决VRP的数学算法。这一类方法称为解析法，是通过建立某种符合逻辑推理的数学模型来解决VRP，具有精确求解的优点，但不足的是，它完全以数学公式的形式存在，所以它不易于理解，不具备良好的人机交互及可视化，也就无法让人直观地感受到所描绘系统是如何运行变化的。相反，仿真方法却可以直观方便地处理问题。

仿真方法是利用以计算机和软件为工具的仿真技术对实际或者设想的系统进行建模并运行，结合某种算法对系统分析，从而得出结果。它结合优化算法来计算模型，则可以求解出最优解。

李先永[6]根据VRP模型，利用EM-Plant仿真软件构建了相应的仿真模型，同时结合启发式求解方法计算和优化，从而验证了该仿真方法的可靠性。刘芳华、杨娟都采用了仿真平台MATLAB结合遗传算法对具体的VRP进行参数输入并运算，得到很好的效果。白雪利用ProModel对某汽车租凭公司的运营方案进行建模优化并评比备选方案，得出最优排程方案。孙姝婷利用 VISSIM微观仿真软件对城市配送线路进行优化搜索，对多条配送路线进行评价分析，为配送车辆选出最优配送线路。陈静静[7]针对定位—路径—库存问题（Location—Routing—Inventory Problem，LRIP）这一物流领域中新的研究热点问题，采用ExtendSim仿真软件构造了该问题的模型，并用软件的遗传算法对其优化计算，求解出LRIP的最优方案。

3 ExtendSim对VRP建模优化

3.1 运输问题

运输问题，解决的是如何组织一个合理的运输方案，使得物资在供求地运送到需求地所需要的总运费最小。其数学模型如下[8]：

设有m个产地，记为A1,A2,…,Am，生产某种物品，可供应产量分别为a1,a2,…,am；有n个需求地，记为B1,B2,…,Bn，其需求量分别为b1,b2,…,bn；供需平衡，即从第i个产地到j个需求地的单位物品的运费为cij，在满足各地需要的前提下，求使得运费最小的调运方案。

设xij（i=1,2,…,n）为第i个产地到第j个需求地的运量，则该运输问题的数学模型可写为：

3.2 对具体问题建模

设有A1,A2两个工厂面向B1,B2,B3三个客户服务，工厂可供应产品数量分别为10,8个单位，客户需求量分别为5,6,7个单位，A1到B1,B2,B3的每单位产品运费分别为3,2,6个单位，A2到B1,B2,B3的每单位产品运费分别为5,3,8个单位。根据以上信息，如何安排一个运输计划，使总运费最少。

对此问题，本文采用ExtendSim仿真软件，实现了模型的整体构建。其整体结构如图1所示。

3.3 模块说明

ExtendSim中的每一个模块都有其特定的功能，这种功能可以是多个的，另外模块内部还有能输入和输出参数的结构。

首先，上述运输问题是一个离散事件，需要放置Executive仿真时钟模块，让软件自动推进事件的发展。两个Create模块表示两个工厂生产产品，Queue模块表示存放产品的仓库，Select item out模块表示选择不同的送货路径，Gate是个路径开关，与Information、Math、Decition共同作用，具有能根据客户是否得到满足而控制路径开通与否的功能。Get模块可设置此路径上每单位产品运费，而Activity模块则是计算运送给某个B客户的总成本，整个产品送货流程以Exit模块结束。

3.4 优化

以上模型只能直观地演示系统的运行，还不能对该系统进行计算最优方案，所以要求解最佳方案，必须使用优化模块Optimizer。

该模块内置遗传算法，在本问题中，有六个决策变量，该模块对这六个量分别随机编码成二进制的基因bi（i=1,2,…,n），并使它们连接组成每一个都拥有六个基因的染色体个体，然后模块自行随机产生初始种群数，再根据目标函数来确定能评价染色体优劣的适应度函数，在本题中以值越小越优，并接着按照一定概率选择较优个体淘汰较劣个体进而产生一个种群，然后按一定概率对这种群里的个体进行交叉、变异运算，最终产生新一代的种群，这一代个体的适应度的数值和平均值都比上一代的有了明显的改进，也就是说向最优值靠拢，接着再继续对这新一代种群不断循环运算，经过运算多代直至不能搜寻到更优的解后，就停止运行并显示最优解了。

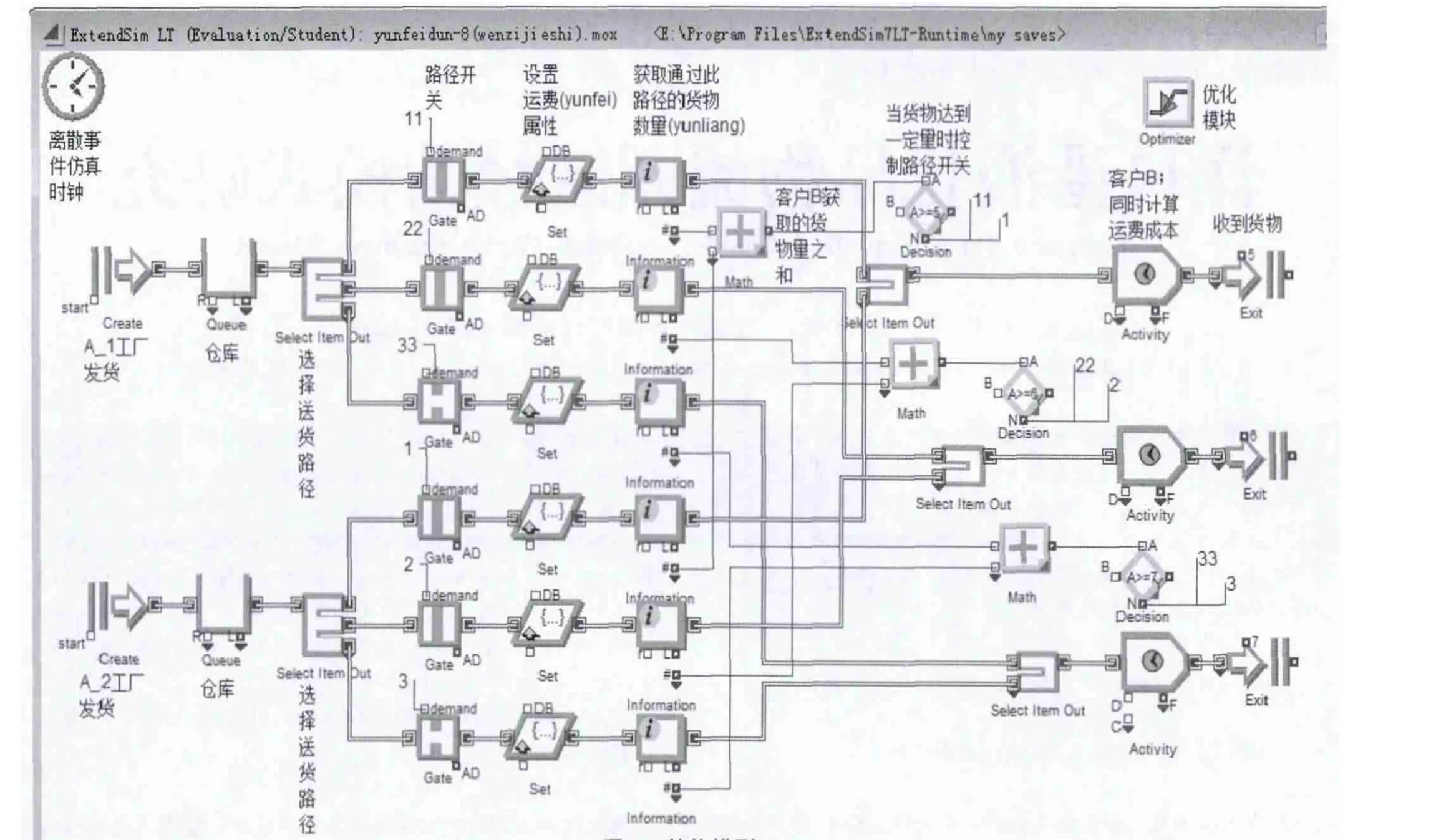
图1 整体模型

在Optimizer的Objectives中，对分别输入运量的最小值0和最大值（客户B的需求量），以及表示总费用最少的目标函数：Mincost=yunfei1+yunfei2+yunfei3。

在Optimizer的Constraints中，输入决策变量的约束条件：

最后，点击New Run，系统自动运行，最终求解出最优结果，结果显示，软件运行了24秒，最小总成本值为82，最优解方案为best行：A1向B1,B2,B3分别运送1、3、6单位的产品；A2向B1,B2,B3分别运送4、3、1单位的产品。

4 结论

本文论述了当前物流领域热点问题车辆路径问题及前人对其研究出来的解决方法，这些方法当中以某种算法来建立数学模型的理论研究居多，仿真建模层面上的研究比较少，因此重点探讨了仿真优化方法在VRP上的应用，并基于ExtendSim仿真优化软件对某一VRP问题进行了建模和优化，得出可靠结果，突显出了仿真软件界面友好、可视化强、操作简单易懂、运算速度快的特点，是解决物流领域中VRP的一种有效的途径。

[1]邓红星，韩锐，武慧荣.物流技术[M].哈尔滨：东北林业大学出版社，2010.

[2]纪红任，游战清，刘克胜,等.物流经济学[M].北京：机械工业出版社，2007.

[3]C.G.Dantzig,J.Ramser.The truck dispatching problem[J].Management Science,1959(6)：80-91.

[4]J Holland.Adaptation in Natural and Artificial System[D].The University of Michigan Press,Ann Arbor,MI,1975.

[5]彭扬，伍蓓.物流系统优化与仿真[M].北京：中国物资出版社，2007.

[6]李永先.车辆路径问题的仿真模型及优化方法研究[D].大连：大连理工大学（博士学位论文），2008.

[7]陈静静.基于ExtendSim的定位—路径—库存问题的仿真研究[D].哈尔滨：哈尔滨工业大学（硕士学位论文），2010.

[8]熊伟.运筹学[M].2版.北京：机械工业出版社，2009.