TBM拦截效果的混合层次模糊综合评估*

胡晓伟，胡国平，王宇晨

(空军工程大学防空反导学院，陕西西安 710051)

0 引言

TBM(tactical ballistic missile)拦截效果评估是反导作战中的一个重要环节，评估的准确性和及时性，影响到战场火力资源的分配、目标二次拦截决策甚至影响整个反导系统和战略要地的安全。国内关于这方面的研究还较少，文献［1-2］针对TBM拦截效果评估模型和流程进行了初步探索，文献［3-6］的研究为TBM拦截效果评估提供了新的思路，具有一定的借鉴意义。但这些研究都不能解决的一个问题是，TBM拦截效果评估过程中有许多影响因素只能进行定性的分析，具有很强的随机性和模糊性，容易受人为主观的影响。为了克服这种不确定性，提高评估结果的准确性，本文将模糊综合评估的方法应用于TBM拦截效果评估。文献［7-12］针对不同的应用环境，运用模糊综合评估较好地解决了各种实际问题。它们在进行模糊评估时通常是固定评估的层次结构，采用不变的单层或多层模型。然而在TBM拦截效果评估中，当各层次指标不同步到达时，这种方法将不再适用。为此，本文提出采用一种混合层次模型的模糊综合评估方法来解决这个问题。

1 TBM拦截效果评估体系分析

1.1 评估体系分析

运用层次分析法对评估体系进行划分。进行TBM拦截效果评估的方法有很多［1-2］，基于可实现性考虑，在此选取红外成像、逆合成孔径雷达(inverse synthetic aperture radar，ISAR)成像和跟踪雷达探测目标运动参数3种方法进行综合评估，3个评估分系统构成评估体系的第1层。每一个分系统都有影响自身评估结果的因素，它们的全体构成评估体系的第2层。TBM拦截效果评估体系层次划分如图1所示。

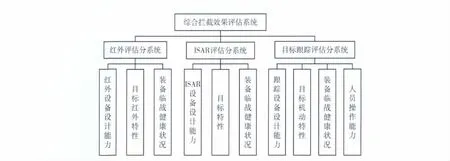
图1 TBM拦截效果评估体系层次划分Fig.1 Levels division of TBM intercepting effect assessment system

1.2 评价指标分析

根据评估体系分析，相应的评价指标如表1所示。

表1 影响评估的评价指标Table 1 Evaluation index affecting assessment

(1)第2层指标分析

从表1可以看出，第2层指标大致可以分为四大类:装备设计能力指标、目标特性指标、装备健康状况指标、人员操作能力指标。这些指标都是定性的指标，难以定量描述，为方便讨论在此统一给出它们的评语集V={良好(v1)，中等(v2)，较差(v3)}。对定性指标的评估是由专家组进行逐项考核评分，最终确定各个指标的评语集。

(2)总指标和第1层指标分析

在拦截效果评估中有以下3种直观的拦截效果:成功拦截，即TBM遭受物理性毁伤;任务拦截，即TBM丧失打击能力;失败拦截，即拦截弹未能命中目标，或打击对目标未造成影响，目标仍能完成既定任务。为精确区分拦截效果，拦截系统采用百分量化模型。针对3种直观的拦截效果分别进行量化:成功拦截的量化值为100，任务拦截的量化值为60，失败拦截的量化值为0。通过对这种直观的效果进行量化，可以将3个评估分系统中不同传感器的观测结果通过相同的量化值对等起来。

然而，为避免采用模糊评估方法时可能出现的“维数灾难”［7］，需要将百分值进行模糊化处理。因此，对总指标和第1层指标取其模糊子集V＇={成功拦截(v＇1)，任务拦截(v＇2)，失败拦截(v＇3)}，下面确定模糊子集中各元素的隶属函数。

Sigmoid型函数和Gauss型函数是较常采用的隶属函数［7］，其函数形式如下。

Sigmoid型函数:

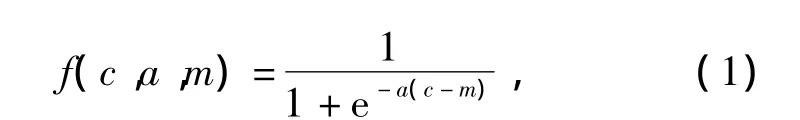
Gauss型函数:

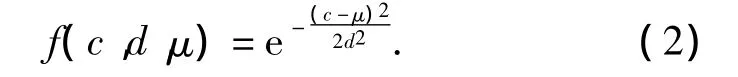
然而通过仿真发现，这种组合的隶属函数存在合成隶属度不恒为1的情况(如图2a)所示)。为解决这个问题，将图2a)中各隶属函数失败拦截f1、任务拦截f2、成功拦截f3分别进行归一化处理，得到改进后的隶属函数 f1'=f1/f，f2'=f2/f，f3'=f3/f，其中f=f1+f2+f3。

图2为改进前后函数对比图，图2b)为改进后模糊子集中各元素的隶属度函数图。

2 TBM拦截效果的混合层次模糊综合评估方法

2.1 模糊综合评估方法模型分析

通常，模糊综合评估的数学模型有单层次模型和多层次模型2种［8］。

(1)单层次模型

设有因素集 U={u1，u2，…，un}，ui表示被考虑的因素，i=1，2，…，n;评语集 V={v1，v2，…，vm}，vj表示评估的结果，j=1，2，…，m;因素集U上的模糊子集 A={a1，a2，…，an}，ai(0≤ai≤1)为因素 ui被考虑的权数。从U到V的一个模糊映射R=(rij)，称为综合评估的评估矩阵，其中rij(0≤rij≤1;i=1，2，…，n;j=1，2，…，m)表示从因素 ui考虑对象被评为vj的隶属度。则当权数A和变换矩阵R都为已知时，应用模糊矩阵的复合运算即可进行模糊综合评估，从而得到模糊综合评估的单层次模型。模型计算公式为

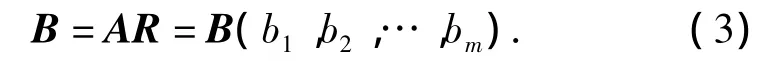
(2)多层次模型

通过对因素集的分层划分，可得到多层次模糊综合评估模型。它是初始模型应用在多层因素上，每一层的评估结果又作为上一层评估的输入，直到最上层为止。在对因素集U={u1，u2，…，un}作一次划分时，可得到二级模糊综合评估模型。其算式为

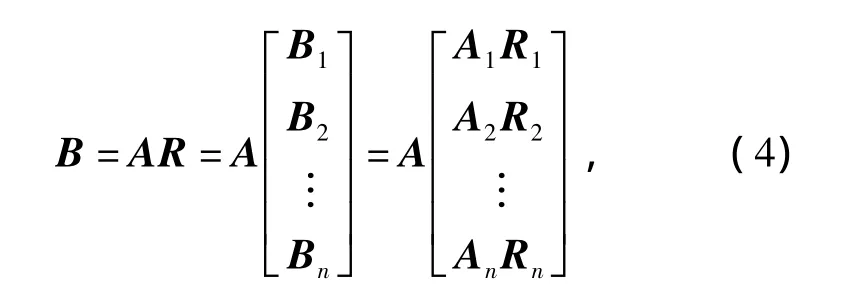
式中:A为 U={U1，U2，…，Ul}中 l个因素的权数分配;Ai为 Ui={ui1，ui2，…，uik}中 k个因素的权数分配;R和Ri分别为U和Ui的综合评估变换矩阵。B则为U的综合评估的结果。

在本文所研究的TBM拦截效果评估体系中，当所有第1层指标可以获取的情况下，可采用单层次模型进行模糊评估;当所有第1层指标无法准确获取的情况下，则可采用二级模型进行评估。然而，当一层指标中仅有部分获取的情况下，以上模型将无法使用。

为解决这个问题，本文提出一种混合层次模型。在该模型中，如果多层模型中，某一层某一个因素的评估输入数据可以直接获取，则用该数据取代下一层的评估结果作为该层评估模型的输入，其他因素仍采用下一层相应的评估结果作为该层评估的输入。如果多个层次有多个因素的评估输入数据可直接获取，则依上述方法逐一进行输入数据的替换，就形成了混合层次的评估模型。

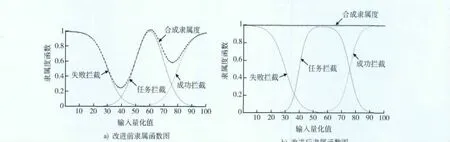
图2 隶属函数图Fig.2 Membership functions

以(2)中二级模糊综合评估模型为例，假设一层因素集中，因素Bi数据可直接得到，则式(4)中AiRi可由Bi取代，此时算式为

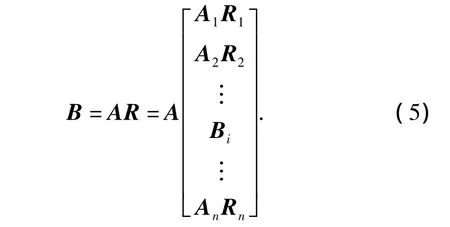
当上述混合层次模型中，所有Bi(i=1，2，…，n)都可获得时，模型即退化为单层次模型;当所有Bi(i=1，2，…，n)均无法得到时，此时模型就变为二级模型。

2.2 基于混合层次模糊综合评估的TBM拦截效果评估模型

基于以上提出的混合层次模糊评估模型，结合TBM拦截效果评估体系的特点，建立的基于混合层次模糊综合评估的TBM拦截效果评估模型如图3所示。

图中A为评估体系第1层指标的权数，A1，A2，A3分别为第2层3组指标的权数;R1，R2，R3分别为第2层3组指标的变换矩阵;b1，b2，b3分别为第1层指标的量化评估值;B1，B2，B3为第2级评估的输出;R为由B1，B2，B3合成的第1层指标的变换矩阵;B为第1级评估的输出，C为最终的百分量化评估结果。

图中实线框中部分完成第1层指标变换矩阵R的合成;虚线框1、虚线框2分别完成对第2层因素指标和第1层因素指标量化评估值的处理。虚线框1和虚线框2共同完成了混合层次模型的第2级评估。

具体评估流程如下:影响拦截效果评估的总因素输入评估模型，如果某一输入因素为第2层评价指标，则经过虚线框1，与相应变换矩阵相乘输出第2级评估值;如果输入因素为第1层指标的量化评估值，则经过虚线框2，进行模糊化处理，输出第2级模糊评估值。输入因素经虚线框1，2处理后的第2级评估输出，在实线框内合成第1层指标的变换矩阵，之后与第1层指标的权数相乘输出第1级评估值，最后再通过重心反模糊化处理，得到最终的百分量化评估结果。

3 仿真分析

3.1 实例仿真

初始变量确定原则:模型变量包括第2层指标权数、变换矩阵和第1层指标权数，以及可能存在的第1层某些指标的量化评估值。权数和变换矩阵由领域内多位专家通过经验集中评议确定，第1层可能存在的量化评估值根据仿真需要给出。

(1)模型变量初始化

第2层指标的权数分别为

第2层指标的变换矩阵分别为

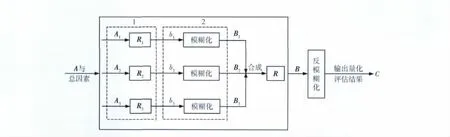
图3 基于混合层次模糊综合评估的TBM拦截效果评估模型Fig.3 TBM intercepting effect assessment model based on mixed levels fuzzy synthetic evaluation

第1层指标的权数为

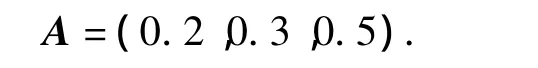
现已获得评估系统部分传感器探测数据:第1层指标ISAR成像结果的量化评估值b2=75。

(2)第2级模糊综合评估计算

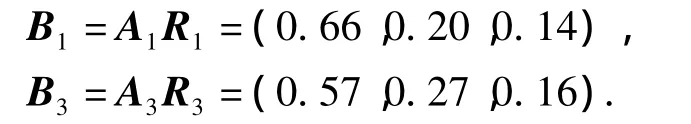
将b2=75代入1.2节中隶属度函数进行模糊化，可得:

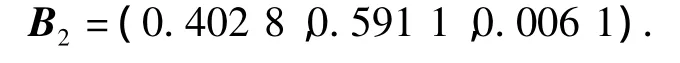
(3)第1级模糊综合评估计算

第1级变换矩阵:

第1级评估输出:

B=AR=(0.537 84，0.352 33，0.109 83).

(4)反模糊化处理

将二级模糊综合评估输出的模糊评估值B，通过求取重心的方法进行反模糊计算，处理过程如图4所示，得到最终百分量化评估结果:C=69.4。

3.2 仿真结果分析

通过以上仿真，可以得出:①模糊综合评估方法可以很好地应用于TBM拦截效果评估领域，并得到最终需要的量化评估结果;②建立的混合层次模型可以解决TBM拦截效果评估过程中各层次指标不同步到达的实际问题;③仿真中最终的量化评估值较好地反映了初始变换矩阵的取值，同时加入了专家对不同指标重要性的评议意见，验证了本文提出的混合层次模糊综合评估方法对TBM拦截效果评估的有效性。

4 结束语

TBM拦截效果评估涉及众多随机性和模糊性因素，本文中建立的评估体系较为全面地反映了各方面因素的影响。模糊综合评估方法可以综合考虑给定对象多种模糊因素并对其进行评价和判别;而提出的混合层次模型紧密联系了评估体系的具体特点，结合这2点建立的基于混合层次模糊综合评估方法的评估模型对TBM拦截效果具有较好的适用性。本文的研究可以为今后TBM拦截效果评估领域的研究提供参考，具有一定的理论和现实意义。

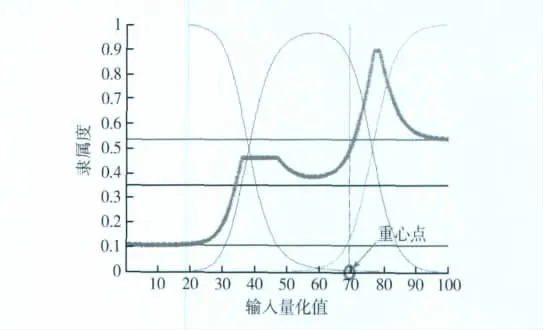
图4 反模糊化处理过程Fig.4 Process of defuzzification

［1］ 胡晓伟，胡国平，王宇晨.反导系统拦截效果综合评估方法［J］.电讯技术，2012，52(2):136-141.HU Xiao-wei，HU guo-ping，WANG Yu-chen.Comprehensive Methods of InterceptingEffect Evaluation in Anti-TBM System［J］.Telecommunication Engineering，2012，52(2):136-141.

［2］ 王森，杨建军，孙鹏.反导作战指控系统对TBM毁伤效果评估［J］.指挥控制与仿真，2011，33(2):14-17.WANG Sen，YANG Jian-jun，SUN Peng.Conspectus of Command and Control System of ATBM to Damage Effect Evaluation of TBM［J］.Command Control＆ Simulation，2011，33(2):14-17.

［3］ 李正东，雍松林，彭文.空中目标毁伤评判问题的探讨［J］.系统工程与电子技术，2002，24(8):24-27.LI Zheng-dong，YONG Song-lin，PENG Wen.Discussion of Aerial Target Quantitative Destruction Estimation［J］.Systems Engineering and Electronic，2002，24(8):24-27.

［4］ LI Xu-hui，CI Lin-lin，LIU Jia-hua，et al.Research on Battle Damage Assessment［C］∥Proceedings of the 7th International Symposium on Test and Measurement，2007:1248-1251.

［5］ 翁弘，任毅，孙进平.一种基于ISAR的目标打击效果评估方法［J］.遥测遥控，2008，29(3):54-59.WENG Hong，REN Yi，SUN Jin-ping.A Battle Damage Assessment Scheme Based on Inverse Synthetic Aperture Radar［J］.Journal of Telemetry，Tracking and Command，2008，29(3):54-59.

［6］ 吴瑕，周焰，崔建，等.导弹防御系统中红外光电识别技术分析［J］.红外与激光工程，2009，38(5):759-766.WU Xia，ZHOU Yan，CUI Jian，et al.Analyses on Infrared Optoelectronics Recognition Technology in Missile Defense System［J］.Infrared and Laser Engineering，2009，38(5):759-766.

［7］ 曾静，张国良，杨春.弹道导弹毁伤效能的模糊综合评估［J］.弹箭与制导学报，2005，25(4):219-221.ZENG Jing，ZHANG Guo-liang，YANG Chun.TBM Damage Efficiency Assessment Based on Fuzzy Synthesized Inference［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25(4):219-221.

［8］ 陈伟，廖洲宝，何海志，等.模糊逻辑推理系统在目标毁伤分析中的应用［J］.电光与控制，2008，15(11):63-66.CHEN Wei，LIAO Zhou-bao，HE Hai-zhi，et al.Application of Fuzzy Logical Inference System in Target Damage Analysis［J］.Electronics Optics ＆ Control，2008，15(11):63-66.

［9］ 姜浩，陈浩光，星学华.基于二级模糊综合评判的机场目标毁伤效果评估［J］.武器装备自动化，2007，26(8):1-2.JIANG Hao，CHEN Hao-guang，XING Xue-hua.Evaluation of Damage Effect for Airport Objects Based on Two-Level Fuzzy Synthesis Evaluation Method［J］.Armament Automation，2007，26(8):1-2.

［10］ 周智超.基于模糊综合评判的舰艇指挥控制效能评估研究［J］.指挥控制与仿真，2006，28(1):7-10.ZHOU Zhi-chao.Study on Command and Control Effectiveness Calculation of Surface Ship Based on the Fuzzy Synthetic Evaluation［J］.Command Control＆ Simulation，2006，28(1):7-10.

［11］ 毕兰金，刘勇志.反舰导弹武器系统作战效能模糊综合评估［J］.弹箭与制导学报，2004，24(1):272-274.BI Lan-jin，LIU Yong-zhi.Fuzzy Multi-Synthesis Assessment of Combat Effectiveness for Antiship Missile Weapon System［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2004，24(1):272-274.

［12］ LI R J.Fuzzy Method in Group Decisionmaking［J］.Computers and Mathematics with Applications，1999，38(1):91-101.