战略战役兵棋系统中的被动声纳探测仿真
董迎涛,柳少军,丁光照,王 燕
(国防大学信息作战与指挥训练教研部,北京 100091)
战略战役兵棋系统是从作战经验、历史经验的角度去思考战争问题,具有抽象程度高、模拟实体多、战场范围广、作战样式全、战场环境复杂等特点,为便于处理,模型采用基于六角格地形的计算方式。被动声纳探测(Passive Sonar Detection)是对水中目标进行远程探测、定位、识别的有效手段,是反潜作战能够取得优势的关键因素。准确有效地仿真被动声纳探测,是反潜作战系统能否反映实际作战过程的重要因素之一。
国外对战略战役反潜作战模拟的研究开展较早,也形成了一些成熟的反潜作战模型,并在一些大型作战模拟系统中进行了验证,如 JWARS,JSIMS 等[1-3]。国内对被动声纳探测的研究主要集中在装备论证或战术运用层面[4-5],还没有比较成熟的战略战役层次的反潜作战模拟系统。本文给出了一种面向战略战役兵棋系统的被动声纳探测仿真模型,对被动声纳的整个探测过程进行了研究,合理考虑了探测过程中的各种影响因素,建立了探测时间模型和海洋声学环境下的噪声传播模型,并进行了验证。
1 被动声纳探测仿真流程
战略战役层次的仿真建模,强调的是对“指挥”或“协同”的模拟,反映了“决策”、“技术”与“技能”兼具的特点。面向战略战役层次的被动声纳仿真模型,模拟的重点是被动声纳系统与战场环境的交互。在实时变化的战场环境条件下,被动声纳探测对作战的影响主要体现在探测时间的变化上。
被动声纳探测仿真流程如图1所示。当系统打开,首先扫描被动声纳探测区域内是否有敌方潜艇存在,扫描到目标后,系统提取潜艇和探测舰艇基本参数和状态参数,计算探测时间,生成探测触发事件。例如,假设某型潜艇在6点时进入被动声纳探测范围区域,模型计算出探测到潜艇需要4h,在各种条件不变的情况下,模型生成一个10点时触发的事件,时间到达,模型输出潜艇相关信息,显示潜艇具体位置。
2 被动声纳探测时间建模
对被动声纳的仿真,主要是模拟海战场环境下被动声纳探测到目标所需要的时间,被动声纳探测时间与被动声纳系统性能、探测目标性能、海洋环境等有关,探测时间根据影响因素的变化而改变。本文用Gamma分布随机变量值来确定被动声纳探测时间。
Gamma分布是统计学的一种连续概率函数,兼有指数分布和幂分布的特点。在被动声纳探测中探测时间主要与被探测目标的类别和噪声值有关,而且目标类别α(形状参数)和最大最小探测时间β(尺度参数)均为定值,其复杂程度(熵)最大,因此被动声纳探测时间的出现概率服从Gamma分布[6]。

图1 被动声纳探测仿真流程图
被动声纳探测时间是指从潜艇进入探测区域到被声纳探测识别定位所用的时间,这里把被动声纳探测、识别、定位三个过程合而为一,被动声纳探测到目标信号,就认为目标已经被识别并定位,系统输出目标信息,屏幕显示目标标识。
2.1 被动声纳探测时间方程
探测一艘潜艇的实际时间是不确定的,是一个随机过程:当一艘潜艇进入探测区域时,先产生一个服从Gamma分布(均值为探测平均最短时间Tmin)的随机变量值作为理论上探测潜艇所需要的最少时间,再产生另一个服从Gamma分布(均值为探测最长时间Tmax)的随机变量值作为理论上探测潜艇所需要的最长时间,然后根据探测时间与噪声的关系,计算出实际探测时间。
被动声纳探测时间与接收到的噪声级存在以下关系:
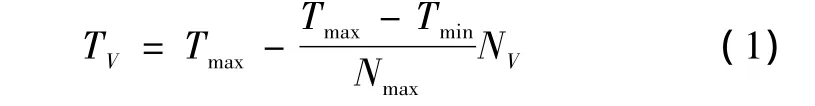
式中,TV为考虑噪声损失时所需的探测时间;NV为声纳接收到的噪声级。
如表1所示,由服从Gamma分布的随机函数产生5组数据,经过噪声损失处理后,得到表中探测时间数据。假设探测平均最短时间为18h,探测最长时间为120h,Gamma分布的形状参数为 3.0。
为便于计算,对表1数据进行平滑,结果是最长探测时间为125h,在最大100dB下探测时间为20h,如图2所示。

表1 被动声纳探测时间数据
如图2所示,当噪声是25dB,则声呐需要98.75h才能发现潜艇。

图2 被动声纳探测时间与噪声关系图
2.2 多重被动声纳探测时间方程
假设同一平台上多个被动声纳同时进行探测,各声纳之间不会形成干扰。此时探测时间的计算有两种可能的方式:一种是各个声纳作为一个独立的整体进行探测,最先探测到目标的被动声纳所用时间即为探测时间;另一种方法是把多个被动声纳看作一个系统,各个被动声纳之间有信息交互。模型使用第二种方法进行多重声纳建模,探测时间方程为

式中,HT为多重声纳同时探测所需时间,H1,…,Hn为各个声纳单独探测所需时间。
2.3 状态改变时探测时间的确定
真实海战中,探测舰艇和目标潜艇状态都在不断地变化。当发生以下情况时,系统将重新计算探测时间,生成探测事件。
·多声纳系统中一个或多个声纳被动打开或关闭;
·声纳毁坏或正在修理中;
·探测舰艇或潜艇航速调整;
·探测舰艇或潜艇进入新的六角格。
再次确定探测时间,并不是丢弃已用的探测时间,而是在此基础上进行计算,运算法则如表2所示。

表2 探测时间运算法则
3 被动声纳探测噪声建模
由方程(2)可知探测时间与被动声纳接收到目标噪声级近似为线性关系。接收到的噪声级主要受目标声源级、传播损失、背景噪声等因素的影响。
被动声纳接收到的噪声级方程为[7]
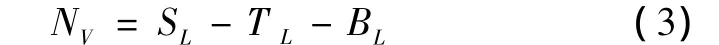
式中,各参数的量纲均为分贝(dB);NV为声纳接收到的噪声级;SL为声源级;TL为传播损失;BL为海洋环境噪声。
3.1 目标噪声声源级SL
根据辐射噪声声源级的大小,潜艇目标可分为四种类型:高噪声潜艇、噪声潜艇、安静型潜艇、极安静型潜艇。考虑辐射噪声随航速的变化特性和临界航速对噪声的影响,声源级方程表示如下[8]:
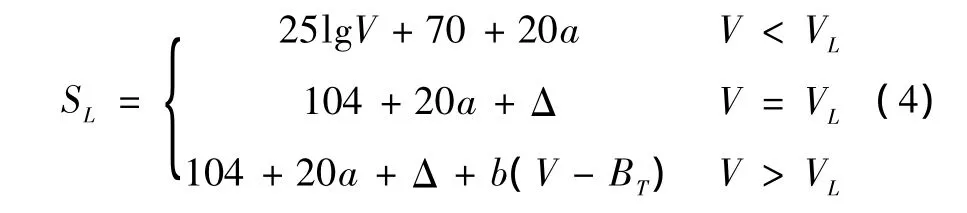
式中,V为潜艇的实时航速;a=1,2,3,4为潜艇的类型级别,分别为极安静型潜艇、安静型潜艇、噪声潜艇、高噪声潜艇;VL是潜艇的临界航速;Δ=20dB-50dB(Δ的选取依据不同类型潜艇的实测数据指标)是潜艇到达临界航速后噪声声源级的增量;b是潜艇达到临界航速后辐射噪声随航速变化的斜率,b∈[1.5,2]。
3.2 传播损失TL
声波在水下的传播主要有三种传播路径:直接路径传播(DP)、海底反射传播(BB)、会聚区传播(CZ)。模型将传播损失按距离分为两个阶段,距声源1m到1000m之间的噪声传播主要为球面扩展损失和吸收损失之和,大于1000m主要为柱面扩展损失和吸收损失之和。
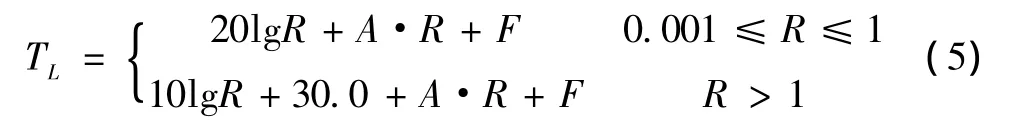
式中,R为传输距离,单位为km;A为吸收系数,取A=2dB/km;F为异常传输损耗,取F=4dB。
3.3 海洋环境噪声BL
海洋环境噪声是指海洋环境中产生的各种声响,是声纳的重要背景噪声,影响声纳的探测距离,干扰声纳系统的正常工作,主要有热噪声、声纳自噪声PN、舰艇噪声VN、其它舰艇噪声SN和海洋动力噪声WN。背景噪声方程为
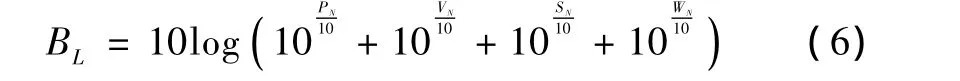
热噪声是个绝对小的量,只有在不存在其它噪声源的情况下才能探测到,与海洋噪声相比,可以忽略。声纳自噪声由具体声纳类型的噪声参数确定。
3.3.1 舰艇平台噪声VN
舰艇平台噪声的声源级是表征舰船声隐蔽性的最基本参数,经验公式为[9]
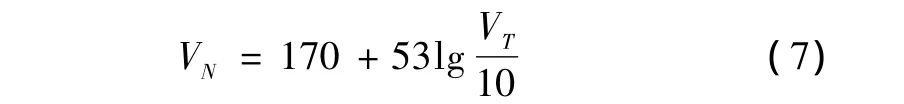
3.3.2 其它舰艇噪声SN
除平台噪声外,作战区域内的其它舰艇产生的噪声同样会对被动声纳探测产生干扰。模型中的其它舰艇噪声是指与探测平台或被探测目标在同一六角格里的舰艇产生的噪声,其它舰艇不予考虑,噪声传播损失计算方程与方程(5)相同。潜艇和舰船噪声方程分别与方程(4)和方程(7)相同。
3.3.3 海洋动力噪声WN
海洋动力噪声主要与风浪和降雨有关,是影响探测潜艇能力的重要部分。表3列出了不同气象条件下海洋动力噪声参数。
4 实例分析
水面舰艇D在某海域执行探测任务,航速为20kn,气象条件为4级海情,小雨。敌方潜艇S以在该区域内低速航行(安静级 a=2,临界航速 VL=11.51kn,Δ =30dB,b=1.8),A1、A2、A3 为区域内的其它舰艇。舰艇部署如图3所示,水面舰艇和潜艇基本参数如表4所示。
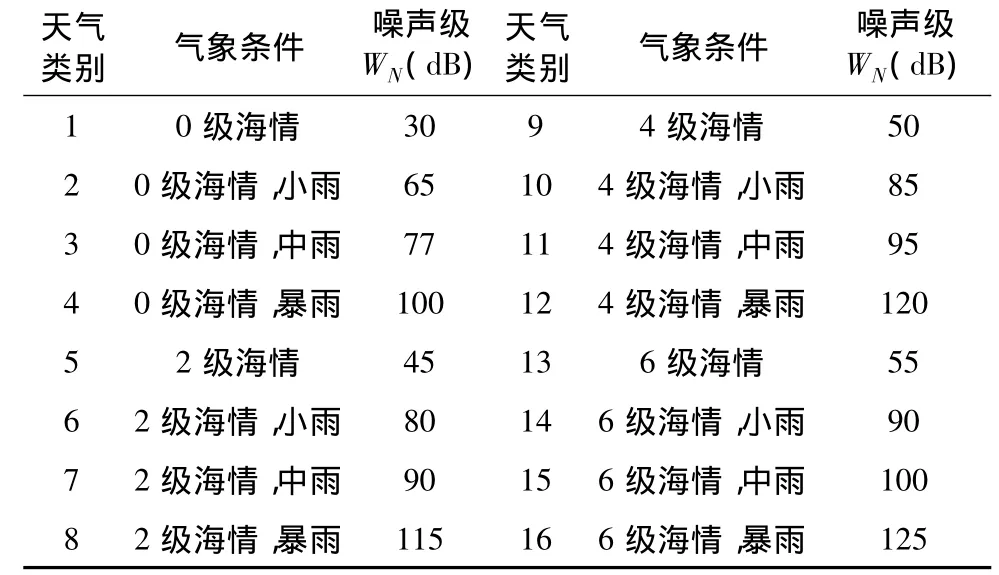
表3 不同气象条件下海洋动力噪声参数表
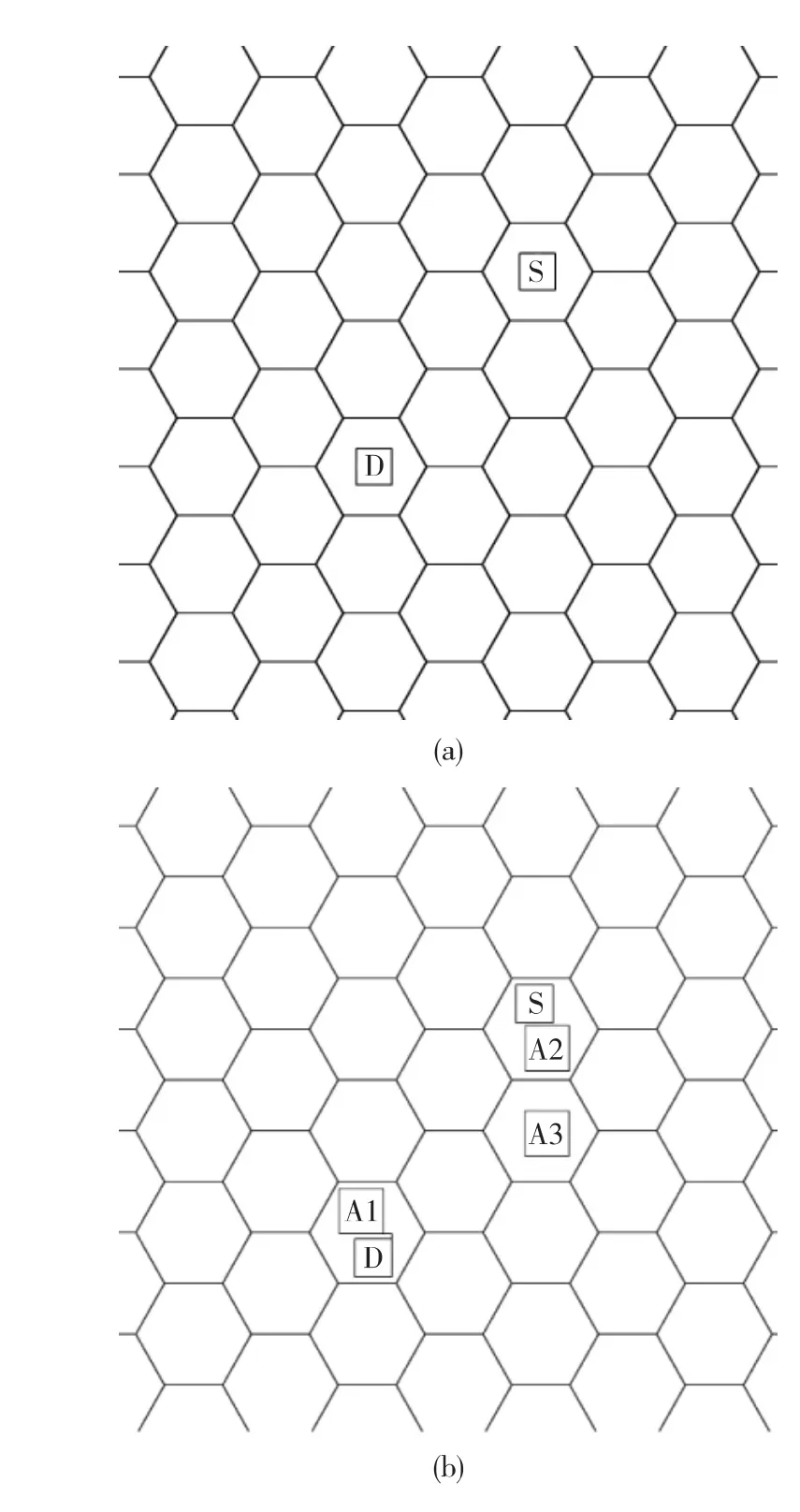
图3 舰艇部署图
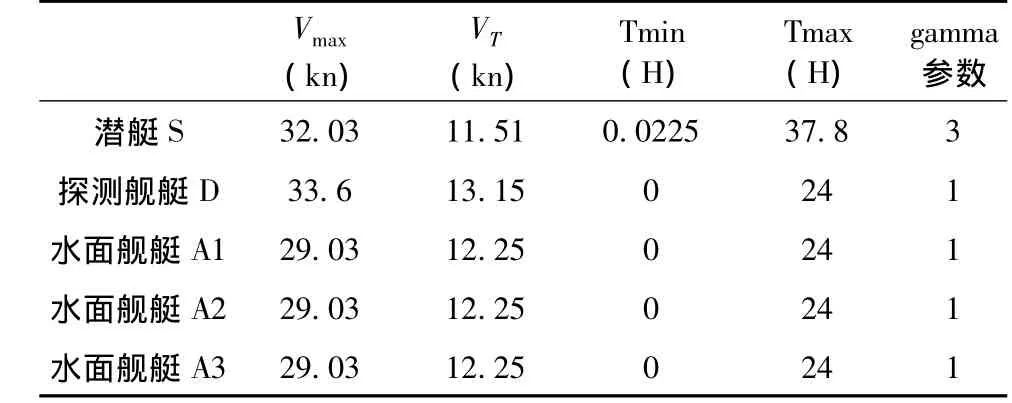
表4 水面舰艇和潜艇基本参数表
想定一:舰艇部署如图3(a)所示,作战初始时间为X月1日0时,作战区域内,只有探测舰艇D,和被探测潜艇S,在舰艇D航速为12kn,潜艇以航速10kn的情况下,探测时间概率密度分布如图4(a)所示。
想定二:舰艇部署如图3(b)所示,作战初始时间为X月2日0时,作战区域内,探测舰艇D与舰艇A1在同一六角格内,被探测潜艇S与舰艇A2在同一六角格内,舰艇A3在其它六角格内,A1、A2、A3航速同为15kn,舰艇D航速为12kn,潜艇以航速10kn,探测时间概率密度分布如图4(b)所示。
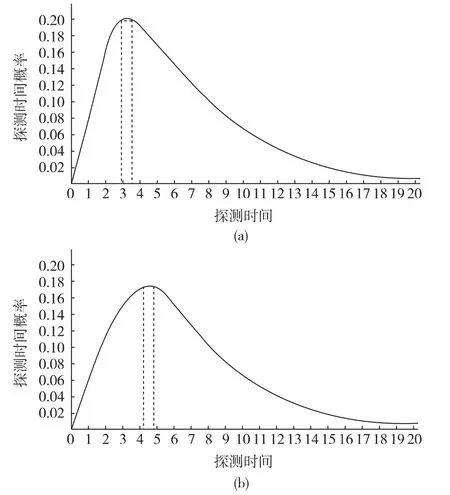
图4 被动声纳探测时间概率密度分布图
由被动声纳探测时间概率密度分布图可知,当没有其它外界因素影响时(想定一),被动声纳连续探测3~4小时时,探测概率最大,为20%左右,如图4(a)所示;当有其它外界因素影响时(想定二),被动声纳连续探测4~5小时时,探测概率最大,为18%左右,如图4(b)所示。
5 结束语
本文结合战略战役层次仿真特点,对被动声纳探测功能进行了分析研究,设计了被动声纳探测仿真模型逻辑框架,建立被动声纳探测仿真模型。根据被动声纳探测时间的随机性,提出了服从Gamma分布的随机探测时间函数,确定了探测时间与噪声的关系方程。同时,根据水下噪声传播特性,建立了海洋环境下的噪声传播方程。
最后,对被动声纳探测仿真模型进行了验证,结果表明被动声纳探测时间随干扰因素的增大而增长,较符合反潜作战实际。除已完成的上述工作外,接下来还需要完成被动声纳探测系统与水面舰艇指挥系统的信息交互工作,建立完整的被动声纳反潜作战模型。
[1]George F.Stone,III Gregory A.McIntyre.The Joint Warfare System(JAWARS):A Modeling and Analysis Tool forthe Defense Department[A].Proceedings of WSC2001[C].691-696.
[2]王小非,陈炜,罗玉臣.海军作战模拟理论与实践[M].北京:国防工业出版社,2010.
[3]金伟新.大型仿真系统[M].北京:电子工业出版社,2004.
[4]邹建,等.水声对抗仿真系统中的被动声纳仿真[J].计算机仿真,2010,27(7):309-312.
[5]李玉阳,宋浩,笪良龙.被动声纳目标识别综合仿真系统[J].计算机工程,2007,33(21):249-251.
[6]张学文.改造后的熵[EB/OL].http://www.moon-soft.com/program/bbs/docelite80144.htm,2000-05-04.
[7]周德生.现代声纳原理[M].武汉:海军工程大学出版社,2004.
[8]高学强,杨日杰.潜艇辐射噪声声源级经验公式修正[J].声学与电子工程,2007(3):17-18.
[9]王德石,等译.实用声纳工程[M].第3版.北京:电子工业出版社,2004.
[10]叶平贤,龚沈光.舰船物理场[M].北京:兵器工业出版社,1992.
[11]George L Ogden,Lisa M Zurk,Mark E Jones,et al.Extraction of Small Boat Harmonic Signatures from Passive Sonar[J].The Journal of the Acoustical Society of America,2011(6):1520-8524.
[12]R Lee Culver,Brett E Bissinger,Alex W Sell.Passive Sonar Tracking Using Sequences of Received Signal Amplitude Fluctuations:Dependence on Environmental Sampling[J].The Journal of the Acoustical Society of America,2011(4):2329.

