基于占有率的信号相位交通状态实时判别模型
聂建强,徐大林
(江苏自动化研究所,江苏 连云港 222006)
交通拥挤已经成为中国众多城市一个普遍的问题。及时、可靠的交通状态信息对于在交通拥挤状态下制定合理的交通疏导策略至关重要。因此交通状态的判别成为了一个重要的研究课题。大量研究人员对该问题进行了深入的研究[1-4]。在文献[2]中,提出了一种基于路段饱和度、排队长度和平均车速的路段交通状态模糊综合评判模型。通过仿真分析认为该模型可以获得不错的效果,但是在国内目前普遍应用的检测手段下排队长度和平均车速这两个交通状态指标并不容易获得,即便可以获得,准确率也很低,难以满足实用的要求。文献[3]提出了一种基于时间占有率-流量比率的路段交通状态判别方法,该方法在实用程度上有了一定的提高,但是对于占有率值和流量比率值的震荡过于敏感,导致判定出的交通状态波动性很大,并不符合人们对交通状态的实际判断。另外,该方法并没有考虑固定检测器的布设位置,红灯时间的存在对占有率值和流量比率值的影响,从而导致流量比率指标值对实际交通状态的反映与实际情况存在完全相反的情况,因此该方法并不具有实用性。文献[4]根据浮动车数据提取路段时间区间内的平均车速来进行路段交通状态的实时判别,该方法考虑了状态变化的连续性,针对交通状态参数的波动性对传统阈值判别法进行了改进。但是在现实情况下,国内大部分地区浮动车数据基本不能获取,从而导致该方法在实际应用中大打折扣。考虑到线圈检测技术已经很成熟且性价比高,且线圈检测器是目前交通控制系统中应用最广的检测手段,本文提出了基于线圈检测器占有率的更加实用可靠的相位交通状态判别模型。
1 基于占有率的相位交通状态判别
1.1 典型路口固定检测器布设
目前,最为成熟可靠的交通检测手段为固定检测器检测,最为常用的检测器有环形线圈检测器和地磁检测器两种。针对当前检测技术的现实情况及结合本文要采用的状态判别方法,对于典型路口的检测器布设如图1所示,路口各个路段分别布设战术检测器和战略检测器。路段各个车道距离停车线1m~2m内布设战术检测器,路段战略检测器的布设位置与路段长度L有关,通过调查分析,在距离路段停车线0.2L距离处(只适用于长度为400m到1000m的路段)的各个车道布设战略检测器[5]。
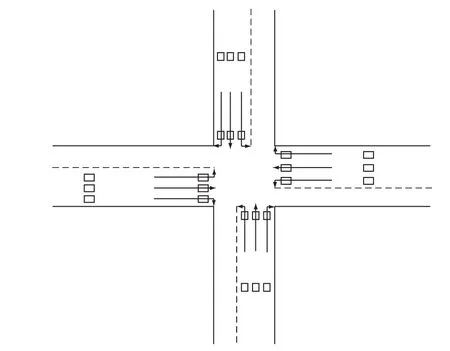
图1 典型路口检测器布设
1.2 交通状态判别指标分析
时间占有率的计算公式如下:
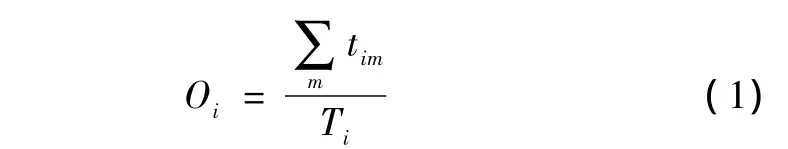
其中,tim为路口相位i第m辆车占据检测器的时间,单位s;Ti为路口相位i的观测时段长,单位s,Oi为路口相位i在Ti内的时间占有率。时间占有率值除了与通过检测器的车流量有关,还与通过检测器的车辆速度有关。车流量和车流速度都是进行道路交通状态判定需要考虑的指标,时间占有率将两者很好地统一了起来,因此时间占有率是很好的道路交通状态判别指标。
战略检测器即安装在距离路口0.2L处的路段上的检测器。战略检测器时间占有率称为战略占有率,受排队长度影响。战略占有率显著上升时,说明战略检测器被车辆长时间占据,可以认为路段排队长度已经过长,路段交通状态已经拥挤。战略占有率越大,路段交通拥挤越严重。
战术检测器即安装在路段出口处距离停车线1m~2m处的检测器。战术检测器时间占有率称为战术占有率,主要受相位绿灯时间内车流量和路段入口前方交通状况影响,两者都将影响战术占有率值的大小。在战略占有率值大到一定程度时,战术占有率值基本保持不变,所以战术占有率值只有在战略占有率值小于一定值时才起作用。
传统的交通状态判别往往倾向于采用饱和度作为交通状态参数,通过对同一实际路口进行交通仿真发现,如图2所示,饱和度和战术占有率对于拥挤状态和非拥挤状态区分度不明显,而战略占有率的区分度非常明显,所以采用战略占有率来判别拥挤状态与非拥挤状态是极为有效的。在非拥挤状态下,路段调查的实际战略占有率往往不能反映路段的实际交通状况,但从图2中不难看出,战术占有率与战略占有率的变化趋势基本一致,相对于饱和度能更好地表现路段交通状态。因此,战术占有率作为非拥挤状态下交通状态参数是合理且合适的。
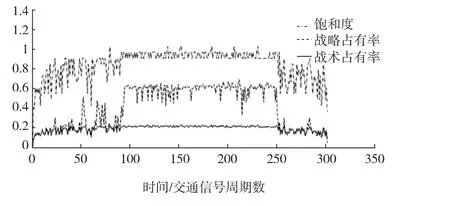
图2 饱和度、战术占有率和战略占有率随时间变化曲线
2 相位交通状态实时判别
2.1 方法概述
基于占有率的相位交通状态实时判别由四部分组成:交通状态预判别,临界值判别,战术占有率变化判别,状态跳跃判别。该方法针对交通状态参数在阈值附近波动性以及状态的跳跃做了优化,方法流程图如图3所示。
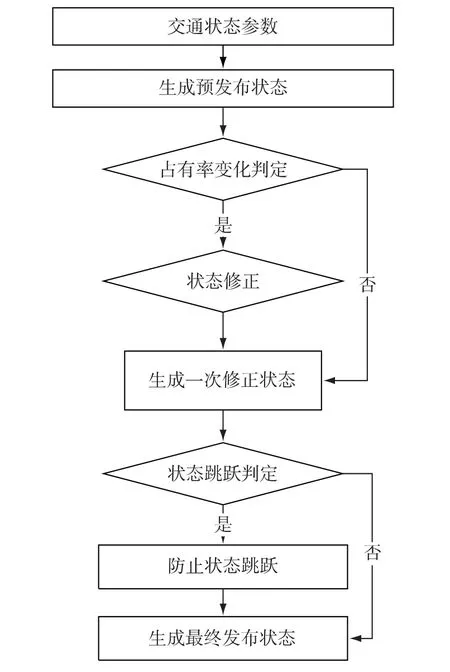
图3 交通状态判别流程
2.2 阈值的确定与交通状态预判别
在本文中,路口某个信号相位在周期时间内的交通状态根据该周期战略时间占有率Oik和周期战术时间占有率O'ik来判定,图4为交通状态判定原理图。拥挤状态与非拥挤状态的临界值用表示,若Oik大于,则相位交通状态判定为拥挤状态。在拥挤状态下,战术占有率与战略占有率不再存在线性关系,此时到达路口交通流量很大,已经接近甚至超过饱和流量,交通流波动性也增强,几乎所有到达路口的车辆都需要停车排队才能通过路口,而且红灯时间排队过长,驾驶员通过路口感到自由度低,并且有一部分车辆需要二次排队[6]。若 Oik小于,则相位交通状态判定为非拥挤状态。Oik、O'ik和的计算公式如下:
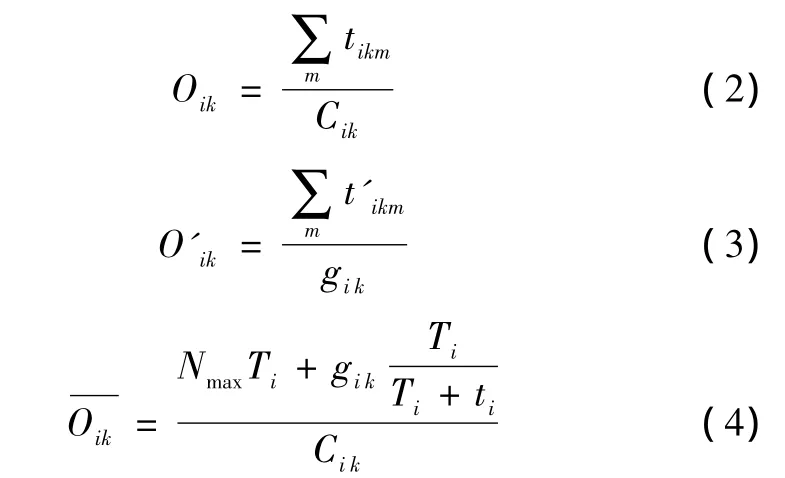
其中,Oik为路口信号相位i的第k个周期的战略时间占有率,O'ik为路口信号相位i的第k个周期的战术时间占有率,tikm为路口相位i第k个周期第m辆车占据战略检测器的时间,t'ikm为路口相位i第k个周期第m辆车占据战术检测器的时间为路口信号相位i的第k个周期的拥挤与非拥挤状态的时间占有率临界值,Cik为路口信号相位i的第k个周期时间,gik为路口信号相位i的第k个周期的绿灯时间,Nmax为路口信号相位i关键车道检测区间所能容纳的最大标准车辆数,Ti为路口信号相位i的标准检测器占有时间,ti为路口信号相位i的标准检测器空档时间。
在交通状态判定为非拥挤状态的情况下,对应相位的战略检测器的时间占有率值的可靠性较低。采用战术检测器时间占有率值与其变化率值相结合的方法,可以更加准确地细分对应相位的空闲状态和顺畅状态。根据我国道路服务水平分级[7-8],在饱和度低于0.42的情况下,道路为空闲状态。根据理论推导,在饱和情况下,战术检测器时间占有率值为Of:
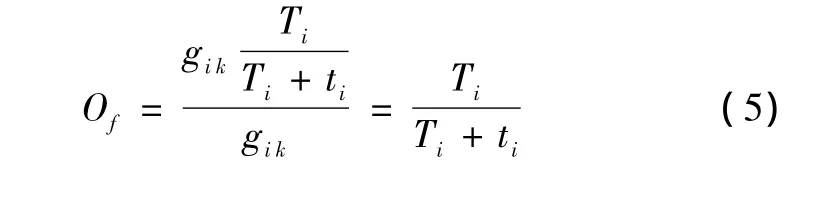
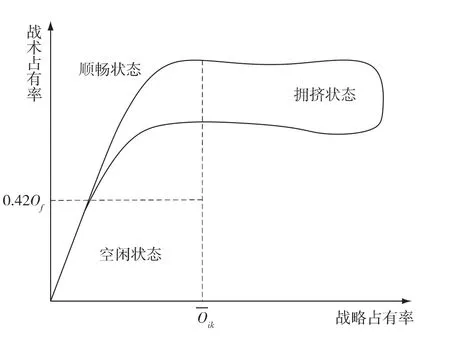
图4 交通状态判定原理
同理,当O'ik小于0.42·Of时,相位交通状态可以判定为空闲,当O'ik大于0.42·Of时,相位交通状态判定为顺畅。在空闲状态下,战术占有率与战略占有率呈线性关系,战术占有率随着战略占有率的上升而呈现急剧上升的态势,此时交通流量小,交通流为自由流,驾驶员进入路口进口道时基本不受交通流中其他车辆的影响,车流波动情况小,且绿灯期间到达的车辆不用尾随排队,可以直接通过路口。在顺畅状态下,战术占有率与战略占有率不再呈现线性关系,而是呈现战术占有率随战略占有率增加而缓慢上升的关系,到达路口的车辆数开始增加,进入路口进口道的车辆开始受其它车辆的影响,可能要减速通过路口,车流的随机性增强,在一个周期内,到达路口的车辆多数能在绿灯时间内全部通过,偶尔出现过饱和排队车辆。综上所述,相位交通空闲时对应交通状态值S=1,相位交通顺畅时对应交通状态值S=2,相位交通拥挤时对应交通状态值S=3。
2.3 近阈值修正
近阈值修正的目标在于判断交通状态参数在阈值附近时的交通状态,避免交通状态值的剧烈波动,因此,本文通过结合占有率和占有率变化趋势来进行相位交通状态判定。假设上一周期的战略占有率为Oi-1,战术占有率为O'i-1,实际判别的交通状态值为Si-1;当前周期的战略占有率Oi,战术占有率为O'i,对应交通状态预判值为Si,记拥挤状态集为S',非拥挤状态集为S″,则一次修正交通状态值S'i的计算如下:

当 Oi≥,Oi-1≥,Oi-Oi-1≥0 时,当前交通状态预判值为拥挤,上一个交通状态预判值也为拥挤,并且交通状态参数战略占有率呈上升趋势,因此,修正交通状态值与上一实际交通判别值无关,与当前交通预判值一致。
当 Oi≤,Oi-1≤,O'i≤,O'i-1≤,O'i-2≤时,当前交通状态预判为非拥挤状态,并且上一个交通状态也预判为非拥挤状态,同时连续三个周期的战术占有率都低于空闲与顺畅状态的战术占有率阈值,则修正交通状态值与上一周期实际交通判别值无关,与当前交通预判值一致。
在其他情况下,修正交通状态值与上一周期的实际交通判别值一致,与当前交通预判值无关。
近阈值修正完毕后获得一次交通状态修正值。
2.4 状态跳跃修正
在实际的交通状态判别中,由于红灯时间对交通的影响,往往造成车辆的排队,导致检测器占有率值的跳变,从而形成交通状态的跳跃,这与实际交通状态的变化趋势是不相符的,因此需要对状态跳跃的情况进行修正。同理,设上一周期的交通状态实际判定为Si-1,当前交通状态的一次修正值为S'i,则交通状态的二次修正值S″i计算如下:
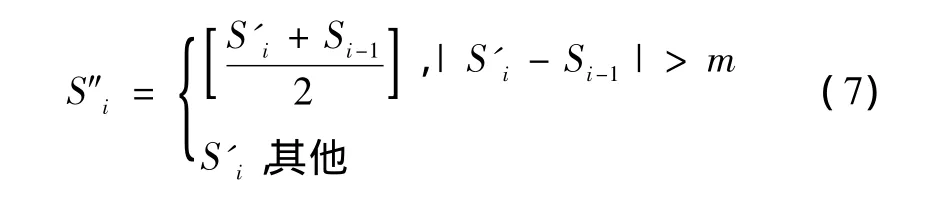
式中,m为状态跳跃判别参数,本文中取值为1,当|S'i-Si-1|>m时,表示状态变化太剧烈,则取状态值的平均值更符合交通状态实际变化规律,否则无须对一次交通状态修正值进行调整,维持不变即可。完成状态跳跃修正后即可生成最终交通状态发布。
3 仿真实验与结果分析
本文以某城市道路交叉口为分析对象,该路口东西方向和南北方向均为双向六车道。针对西东向左转相位进行交通状态判别,采用VISSIM4.2仿真软件对该路口进行仿真实验,仿真交叉口如图5所示,分别只基于占有率值进行交通状态判别和基于占有率值及其修正进行交通状态判别,得到交通状态判别结果图6和图7。
从图6和图7中可以看出,只基于占有率值的交通状态判别波动性较大,基于占有率值及其变化率判别的交通状态稳定性强,更符合路口的实际情况。图7相对于图6做了6次修正,基本消除了状态的突变及跳跃情况,可以证明本文所提模型对改进交通状态判别的有效性。

图5 仿真交叉口
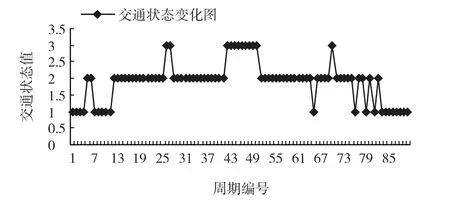
图6 基于占有率值的交通状态传统判别结果
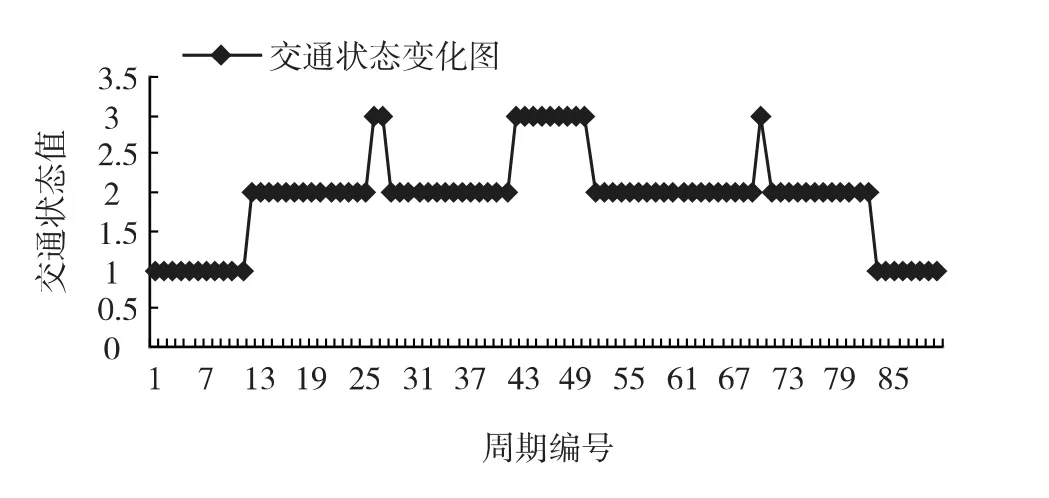
图7 基于占有率值及其修正的状态判别结果
4 结束语
相位交通状态信息对于制定合理有效的交通疏导策略意义重大。本文提出采用单车道双检测器信息采集模型,并且根据双检测器采集的时间占有率信息来进行相位交通状态判别。本文的创新之处在于提出了阈值确定模型,阈值的确定不完全靠主观经验,需要结合实地调查与理论公式来计算得出,并且针对交通状态参数在阈值附近的波动和跳跃进行了状态修正,使得判别出的交通状态连续性更好。本文通过VISSIM4.2仿真模拟实际路口,对传统的占有率阈值判别法和本文提出的基于占有率和占有率变化的判别法进行了对比,结果发现,后者相对于前者更能准确有效地判别相位的交通状态。可进一步结合历史数据库来对当前状态进行判别,对阈值进行动态修正等。
[1]王子纲,施鹏飞,胡福乔.基于相位饱和度的城市交通拥塞的定理评价方法[J].微型电脑应用,2002,18(1):16-18.
[2]杨兆升,张茂雷.基于模糊综合评判的道路交通状态分析模型[J].公路交通科技,2010,27(9):121-126.
[3]陈宁宁.信号控制子区动态划分及区域自适应协调控制研究[D].广州:中山大学,2010.
[4]王吟松,王嘉文,张建跃,等.基于浮动车车速数据的交通状态实时判别系统和方法[J].交通信息与安全,2011,29(6):97-102.
[5]王春娥.基于数据融合的城市道路交通状态判别算法研究[D].长春:吉林大学,2008.
[6]Yaser E.Hawas.A Fuzzy-based System for Incident Detection in Urban Street Networks[J].Transportation Research Part C 15(2007)69-95.
[7]Reilly,W.Highway Capacity Manual[M].Transportation Research Board,National Research Council,1998-4-1.
[8]公安部,建设部.城市道路交通管理评价指标体系[M].北京:公安部交通管理局、建设部城市建设司,2005.

