高压下TiAl3结构及热动力学性质的第一性原理研究*
王海燕 历长云 高洁 胡前库 米国发
(河南理工大学材料科学与工程学院,焦作 454000)
1 引言
钛铝系金属间化合物主要包括Ti3Al,TiAl和TiAl3三种,其中TiAl3具有D022超点阵结构,可看作是Ll2超点阵的衍生结构,即在Ll2超点阵结构的(001)面引入位移矢量为1/2〈110〉的反相畴界获得.它是含铝量最多的金属间化合物,其密度(3.3 g/cm3)比TiAl还小,抗氧化性随着Al含量的增加也得到了明显的改善,而且Ti在Al中的扩散速率低,TiAl3与Al基体的错配度小(2.0%),优越的性能明显超过其他同类合金,这使得TiAl3成为潜在的低密度高温结构材料.但是由于室温塑性、韧性太低,所以目前还处于基础研究阶段,尚未实现广泛应用[1,2].
为解决上述问题,多年以来,国内外学者对TiAl3金属间化合物进行了大量的探索和研究,其中很多研究致力于对其结构相稳定性和电子性质的理解方面[3−8].为了改善TiAl3的塑形,科研人员添加了C[9],Si[10,11],Cr[12]等合金元素,对加入合金元素后的扩散机制、掺杂占位、反应机制等进行了研究.目前,对于TiAl3化合物的研究主要是常压下的研究,而对于高压下其结构和性质研究还较少.特别是对于高压下TiAl3金属间化合物热力学性质的研究,实验上存在着较大的困难,相关报道很少.而第一性原理计算是一种可行的方法,已经成功用于研究高压下材料的物性[13,16].本文利用基于密度泛函理论的第一性原理方法研究了D022结构TiAl3的基本结构性质,通过准谐德拜模型研究了其热动力学性质,如状态方程、热膨胀系数和热容等,并与TiAl金属间化合物的热动力学性质进行了对比.
2 计算方法
在电子结构总能量的计算中,本文采用基于平面波赝势的密度泛函理论计算方法,使用由Vanderbilt建立的非局域超软赝势[17]和PBE广义梯度近似交换相关函数(PBE-GGA)[18].在电子结构计算中,平面波截断能取350 eV,Ti,Al的价电子分别为3s23p63d24s2和3s23p1.在TiAl3金属间化合物D022结构计算中,布里渊区采用8×8×8 Monkhorst-Pack[19]形式的特殊K点.总能量差小于5×10−7eV/Atom时认为达到自洽收敛.
我们采用准谐德拜模型[20]研究TiAl3的热力学性质.在此模型中,TiAl3的非平衡Gibbs函数G∗(V,P,T)形式如下:

在等式(1)的右边,E(V)表示每个原胞的总能量,P,V分别表示压强和体积,AVib是振动的Helmholtz自由能.考虑到准谐近似并使用声子态密度的德拜模型,AVib可用如下形式表示[21,22]:
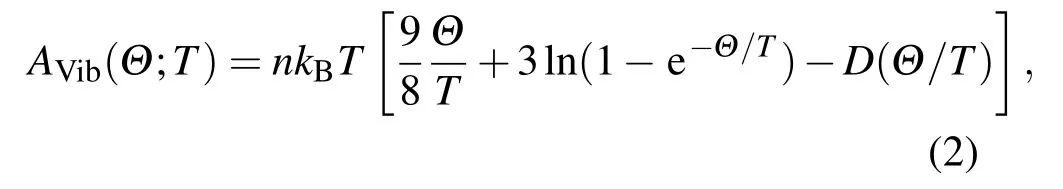
其中Θ(V)是德拜温度,D(Θ/T)是德拜积分,n是每个原胞中包含的原子数.对于各向同性的固体来说,Θ可表达为[21]

M是分子的质量,σ是泊松比率(Poisson ratio),其值取为0.25[23],f(σ)和BS参阅文献[24].BS是用来表示晶体压缩率的绝热体弹模量,可以表示为

非平衡Gibbs函数G∗(V,P,T)对体积求最小值,即

通过(5)式可以得到热状态方程,且等温弹性模量BT,热容CV,热膨胀系数α分别用如下形式表示:

其中γ是格林爱森(Grüneisen)参数.
3 结果与讨论
3.1 D022结构TiAl3的基本物性
TiAl3金属间化合物具有D022结构,属于I4/mmm(#139)空间群,晶胞由两个面心立方格子堆叠构成,晶胞中有2个Ti原子和6个Al原子,Ti原子占据晶胞的角顶位置和中心位置,Al原子分别占据了晶胞的两个面心立方格子除堆叠界面中心外的所有面心位置以及堆叠界面4个角顶位置,如图1所示.

图1 TiAl3的晶体结构,灰色小球表示Al原子,黑色小球表示Ti原子
将计算的总能量E和晶胞体积V用Birch-Murnaghan状态方程进行拟合,其关系式如下[25]:

其中,E0是零压下的静态能量,Vn=V/V0是相对体积,压强和相对体积的关系如下:

D022结构TiAl3在零压和0 K下的晶格常数、体弹模量B0及其对压强的一阶导数,如表1所示.从表1中可以看出,我们计算得到的晶格常数a,c轴比率c/a,体弹模量B0及其对压强的一阶导数与实验结果和其他理论计算结果符合得很好.
图2给出了计算的TiAl3总能量和体积的关系.其中,实心点表示本文的计算结果,空心点表示Boulechfar等[30]使用GGA方法的计算结果,E0表示TiAl3在0 K下最稳定结构的原胞总能量.从图中可以看出,原胞体积对应的总能量减去最稳定结构原胞的总能量的差值在原胞体积62—65Å3之间存在最低点,实验上测得原胞体积V0=63.75Å3,可以看出我们的计算结果比Boulechfar等的计算结果更加接近实验值.
表1 TiAl3在零压和0 K下的晶格常数a,c轴比率c/a,体弹模量B0和体弹模量对压强的一阶导数
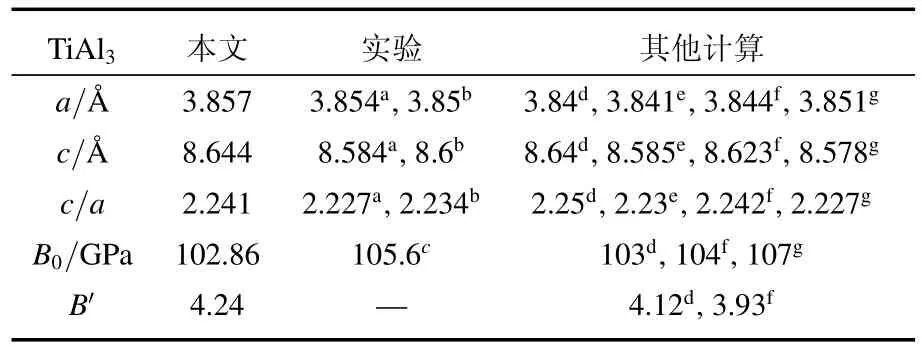
表1 TiAl3在零压和0 K下的晶格常数a,c轴比率c/a,体弹模量B0和体弹模量对压强的一阶导数
aRef.[26]; bRef.[9]; cRef.[27]; dRef.[28]; eRef.[29]; fRef.[30];gRef.[31].
TiAl3 本文 实验 其他计算a/Å3.8573.854a,3.85b3.84d,3.841e,3.844f,3.851g c/Å8.6448.584a,8.6b8.64d,8.585e,8.623f,8.578g c/a 2.241 2.227a,2.234b 2.25d,2.23e,2.242f,2.227g B0/GPa 102.86 105.6c 103d,104f,107g B′ 4.24 — 4.12d,3.93f
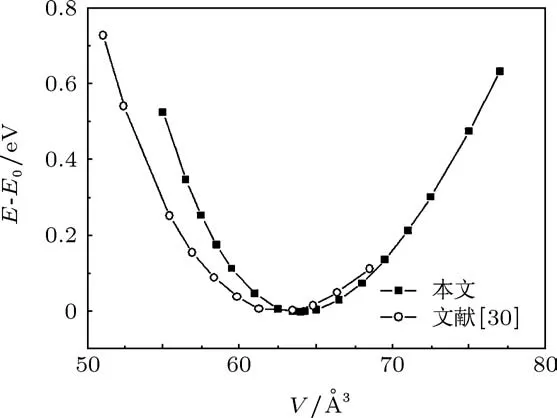
图2 TiAl3原胞的总能量随体积的变化关系
3.2 TiAl3的热动力学性质
3.2.1 状态方程
TiAl3在不同温度和压强下的相对体积与压强的关系如图3所示.从图3(a)中可知,在等温压缩下,TiAl3的相对体积V/V0随压强P增加近似线性下降,温度越高,曲线的斜率越大,表明温度越高TiAl3金属间化合物越容易压缩.从图3(b)的等压曲线得知,TiAl3的相对体积V/V0随温度T增加而增大,在低压下曲线变化比高压下明显.体积随压强增加而降低,随温度降低而减小,说明增加压强与减小温度的效应是相同的.
3.2.2 体弹模量B0
为了更进一步研究TiAl3的结构性质,通过准谐德拜模型计算了TiAl3的体弹模量B0随压强和温度的变化关系,如图4所示.从图中可以看出,体弹模量B0随压强的增大近似线性增大,在给定的压强下体弹模量B0随温度的增加急剧下降,且低压下体弹模量下降比高压下明显.当P=0 GPa时,体弹模量在1500 K和0 K之间的差值为24.28 GPa,当压力P=18 GPa时,二者之间的差值仅为2.37 GPa.此外,在低温下体弹模量随压强呈线性增大,高温下体弹模量随压强的变化不再是线性关系,高温低压下曲线的斜率要大于高温高压下的斜率.图中空心点表示Boulechfar等[30]在0 K下的计算结果,与我们的结果非常符合.

图3 (a)不同温度下,TiAl3金属间化合物D022结构的V/V0与压强的变化关系;(b)不同压强下,TiAl3金属间化合物D022结构的V/V0与温度的变化关系;其中V表示任意温度下的体积,V0表示零温下的体积
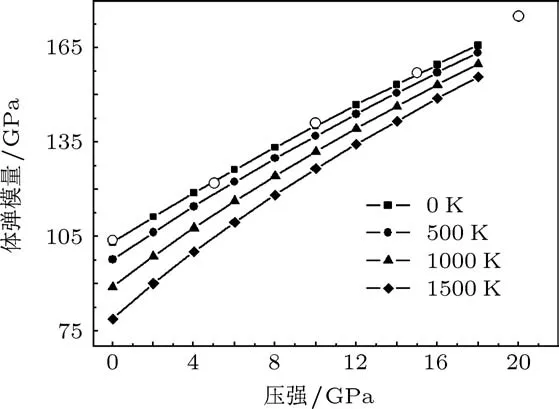
图4 TiAl3的体弹模量B0在温度为0,500,1000和1500 K时随压强的变化关系(空心点表示Boulechfar等[30]0 K下的计算结果)
3.2.3热膨胀系数
D022结构TiAl3的热膨胀系数α随压强和温度的变化关系曲线如图5所示.可以看出,对于一个给定温度,热膨胀系数α随着压强的增大而急剧地减小,特别是在高温下越明显.对于一个给定压强,α随着温度的增加而增加,在低温下变化迅速,呈指数形式增加,在高温部分随温度的变化变得平缓,趋于线性增加.尤为明显的是,当压力P>8 GPa时,TiAl3的热膨胀系数在600 K和1500 K之间变化很小(P=18 GPa时仅为1.5×10−6K−1),这说明在高压下,温度对热膨胀系数的影响非常小.

图5 TiAl3的热膨胀系数α(10−5K−1)随压强和温度的变化关系

表2 TiAl3和TiAl在不同压强和不同温度下的热膨胀系数α(10−5K−1)
为了更好地研究金属间化合物TiAl3的热力学性质,我们将本文的计算数据和以前计算的TiAl的数据[32]进行了比对.表2列出了金属间化合物TiAl3和TiAl在不同的温度(300,600,900,1200,1500 K)和压强(0,4,8,12,16 GPa)下的热膨胀系数.零压常温下金属间化合物TiAl3和TiAl的热膨胀系数α的值分别为1.95×10−5K−1和1.58×10−5K−1.在0 GPa下,金属间化合物TiAl3的热膨胀系数总是高于TiAl;随着温度的升高和压强的增大,金属间化合物TiAl3的热膨胀系数慢慢低于TiAl的热膨胀系数.压强为0,4,8,12,16 GPa时TiAl3的热膨胀系数从300 K到1500 K分别增加了40.55%,34.62%,32.62%,31.85%,30.88%;TiAl的热膨胀系数分别增加了47.85%,45.66%,43.84%,42.78%,42.53%.这意味着升高温度时,TiAl的热膨胀系数增大的速度高于TiAl3,且随着压强的增大温度效应变小.
3.2.4 热容
在表3中,我们列出了金属间化合物TiAl3和TiAl在不同的温度(300,600,900,1200,1500 K)和压强(0,4,8,12,16 GPa)下的热容CV.在零压常温下,TiAl3的热容CV为 80.76 J/mol−1·K−1.压强从0 GPa增加到16 GPa,在300,600,900,1200和1500 K,金属间化合物TiAl3的热容CV分别减小了9.27%,2.67%,1.25%,0.72%,0.39%;金属间化合物TiAl的热容CV分别减小了6.76%,2.03%,0.96%,0.55%,0.39%.随着压强的增大,热容CV在低温减小得比在高温下多,原因在于增加压强和降低温度对材料来说是等效的.对比相同温度下金属间化合物TiAl3和TiAl的热容值,发现TiAl3的热容值近似为TiAl的二倍.

表 3 金属间化合物 TiAl3 和 TiAl的热容 CV(J·mol−1·K−1)随压强和温度的变化关系
4 总结
采用第一性原理平面波赝势密度泛函理论研究了TiAl3金属间化合物D022结构的基本结构性质,计算得到的晶格常数a,c体弹模量B0,体弹模量对压强的一阶导数B′0与实验值和其他理论值符合得很好.
通过准谐德拜模型,成功地得到了相对体积V/V0与压强和温度的关系以及弹性模量、热膨胀系数和热容与压强和温度的关系.计算结果显示,弹性模量B0随压强的增大近似线性增大,在给定的压强下弹性模量B0随温度的增加急剧下降;在低温下体弹模量随压强呈线性增大,高温下体弹模量随压强的变化不再是线性关系,高温低压下曲线的斜率要大于高温高压下的斜率.通过对比高温高压下TiAl和TiAl3的热膨胀和热容,发现在0 GPa下,金属间化合物TiAl3的热膨胀系数总是高于TiAl,随着温度的升高和压强的增大,金属间化合物TiAl3的热膨胀系数慢慢低于TiAl的热膨胀系数;相同温度下TiAl3的热容值近似为TiAl的二倍.
[1]Zhang Y G,Han Y F,Chen G L 2001 Structural Materials of Intermetallics(Beijing:National Defense Industry Press)(in Chinese)[张永刚,韩雅芳,陈国良2001金属间化合物结构材料(北京:国防工业出版社)]
[2]Yamaguchi M,Umakoshi Y,Yamane T 1987 Philos.Mag.A 55 301
[3]Asta M,Fontaine D,Schilfgaarde M,Sluiter M,Methfessel M 1992 Phys.Rev.B 46 5055
[4]Bastow T J,Foewood C T,Gibson M A,Smith M E 1998 Phys.Rev.B 58 2988
[5]Amador C,Hoyt J J,Chakoumakos B C,de Fontaine D 1995 Phys.Rev.Lett.74 4955
[6]Lue C S,Xie B X,Horng S N,Su J H,Lin J Y 2005 Phys.Rev.B 71 195104
[7]Saniz R,Ye L H,Shishidou T,Freeman A J 2006 Phys.Rev.B 72 014209
[8]Hong T,Watson-Yang T J,Guo X Q 1991 Phys.Rev.B 43 1940
[9]Viala J C,Peillon N,Clochefert L,Bouix J 1995 Mater.Sci.Eng.A 203 222
[10]Zhu G L,Dai Y B,Shu D,Xiao Y P 2011 Comput.Mater.Sci.50 2636
[11]Zhu G L,Shu D,Dai Y B,Wang J,Sun B D 2009 Acta Phys.Sin.58 S210(in Chinese)[祝国梁,疏达,戴永兵,王俊,孙宝德2009物理学报58 S210]
[12]Kogachi M,Kameyama A 1995 Intermetailics 3 327
[13]Ming X,Wang X L,Du F,Chen G,Wang C Z,Yin J W 2012 Acta Phys.Sin.61 097102[明星,王小兰,杜菲,陈岗,王春忠,尹建武2012物理学报61 097102]
[14]Wang B,Liu Y,Ye J W 2012 Acta Phys.Sin.61 186501(in Chinese)[王斌,刘颖,叶金文2012物理学报61 186501]
[15]Du H J,Guo L C,Li D C,Yu D L,He J L 2009 Chin.Phys.Lett.26 016403
[16]Hao A M,Zhou T J,Zhu Y,Zhang X Y,Liu R P 2011 Chin.Phys.B 20 047103
[17]Vanderbilt D 1990 Phys.Rev.B 41 7892
[18]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865
[19]Monkhorst H J,Pack J D 1976 Phys.Rev.B 13 5188
[20]Blanco M A,Francisco E,Luana V 2004 Comput.Phys.Commun.158 57
[21]Blanco M A,Martín Pendás A,Francisco E 1996 J.Molec.Struct.:Theochem 368 245
[22]Flórez M,Recio J M,Francisco E,Blanco M A 2002 Phys.Rev.B 66 144112
[23]PoirerJP1991IntroductiontothePhysicsoftheEarth’sInterior(England:Cambridge University Press)
[24]Francisco E,Blanco M A,Sanjurjo G 2001 Phys.Rev.B 63 094107
[25]Murnaghan F D 1944 Proc.Natl.Acad.Sci.USA 30 244
[26]Srinivasan S,Desch P B,Schwartz R B 1991 Scr.Metall.Mater.25 2513
[27]Nakamura M,Kimura K 1991 J.Mater.Sci.26 2208
[28]Ghosh G,van de Walle A,Asta M 2007 J.Phase.Equil.Diffu.28 9
[29]Zhang H,Wang S Q 2010 J.Mater.Sci.Technol.26 1071
[30]Boulechfar R,Ghemid S,Meradji H,Bouhafs B 2010 Physica B 405 4045
[31]Kraj`eí M,Hafner J 2002 J.Phys.Condens.Matter 14 024101
[32]Li X S,Wang H Y,Li C Y,Mi G F,Hu Q K 2012 Commun.Theor.Phys.57 141

