太赫兹波段谐振频率可调的开口谐振环结构*

戴雨涵 陈小浪 赵强 张继华 陈宏伟 杨传仁

(电子科技大学，电子薄膜与集成器件国家重点实验室，成都 610054)

(2012年8月6日收到;2012年9月21日收到修改稿)

1 引言

左手材料 (left-handed metamaterials，LHMs)是一种介电常数ε和磁导率µ同时为负的人工周期结构材料[1-3].1968年，苏联物理学家Veselago[4]首先研究了左手材料的基本理论问题.随后，英国物理学家Pendry等[5,6]于1996年相继提出：由周期性排列的金属线和金属谐振环组成的介质，其等效介电常数和等效磁导率在微波段为负值.在该理论基础上，Shelby等[7]用金属线和开口谐振环(SRRs)阵列组合成功制备了世界上第一块人造左手材料.近年来，随着左手材料独有的物理特性被人们逐步认识，围绕左手材料的各项研究也迅速展开，并不断促进着这一新兴领域的飞速发展.

左手材料对电磁波的响应特性始终是人们关注的重点.由于左手材料的特征峰主要取决于开口谐振环SRRs的磁谐振频率，因此深入研究SRRs的磁谐振行为对于左手材料的研制具有重要的科学意义和应用价值.目前已有的研究结果主要集中在SRRs的结构参数，如线宽、开口大小及内外环间距等方面[8-10].关于SRRs基底或表面覆盖物材料对谐振的影响方面，也有了一定程度的研究[11].在掌握了左手材料对电磁波响应规律的基础上，一个需要重视并解决的问题(也是SRRs结构在设计过程中应当注意的)，便是如何实现器件小型化.随着电子通讯技术的不断发展及微细加工工艺的日益成熟，体积小型化已成为电子元器件的发展趋势和必然要求，能否有效控制左手材料的体积尺寸，已成为影响其实际生产使用的关键因素.通过加载高介电常数基底，可以降低左手材料的谐振频率，减小器件尺寸，但高介电常数基底会导致损耗的增大，降低器件工作效率.所以寻找合适的结构是解决器件小型化问题的主要途径之一.

本文提出在SRRs两环间隙内引入相对交错的金属短线，并对因金属短线的加入所引起的电磁波透射性能变化进行研究，最终得到了工作在太赫兹波段的新型SRRs结构单元.通过与传统SRRs结构比较发现，新结构能以更小的尺寸在相同频率下发生谐振.因此，新型SRRs结构在体积小型化方面具有明显优势，并为今后的实际使用提供了有意义的参考.

2 数值模拟及讨论

2.1 SRRs模型

模拟中采用的一系列磁谐振单元是由传统的SRRs和两环间相对交错的金属短线构成，共5种结构，其短线数目N分别为 0，10，14，22，及 26，具体结构见图1，图2.SRRs的边长L=30µm，线宽W=3µm，开口宽度Gp=4µm，两环间距G=3.5µm.金属短线的长Lx，宽Wx及间距Gx分别为 3，2和 0.5µm.

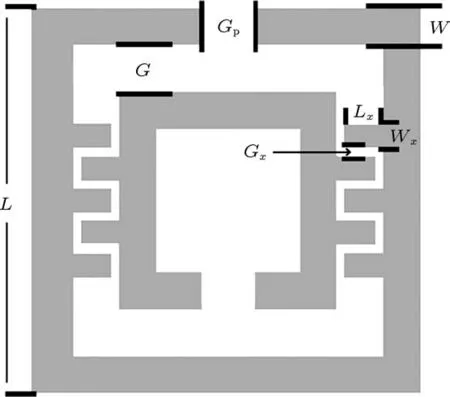
图1 含有10支金属短线的SRRs

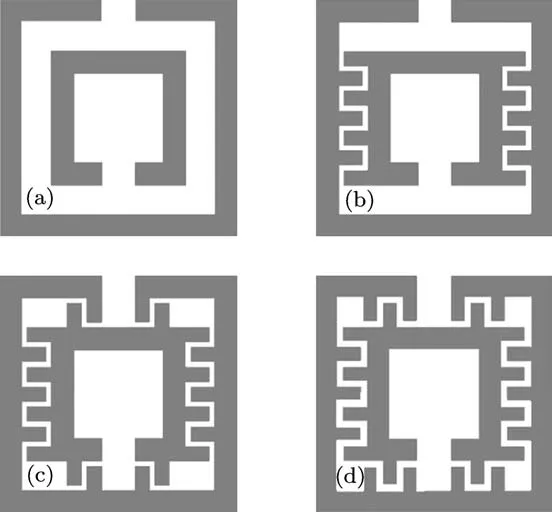
图 2 (a)无金属短线 SRRs;(b)，(c)，(d)短线数目为 14，22，26的SRRs

本文的数值仿真采用基于有限元积分技术的商业软件CST Microwave Studio.仿真时，边界条件如图3所示，电磁波沿x方向传播，电场沿y方向，磁场沿z方向.为了避免基底对SRRs的迟滞效应，对以上单元的数值仿真均在真空中进行，无介质基底，金属为铜，电导率为5.8×107S·m.

2.2 金属短线数目对谐振频率的影响

在传统SRRs两环间添加相对交错的金属短线，添加数目分别为10，14，22及26.对以上几种SRRs结构的电磁波透射特性进行数值模拟，并将结果与传统SRRs比较，结果如图4所示.当金属短线数目N=0，即传统SRRs，其电磁波透射曲线在1.22 THz出现一个谷值，说明在该频点发生谐振.而在两环间添加金属短线且数目不断增大时，谐振频率显著降低.当添加26支短线时，谐振频率降至0.72 THz，降幅达到40.98%.

图3 SRRs单元边界条件

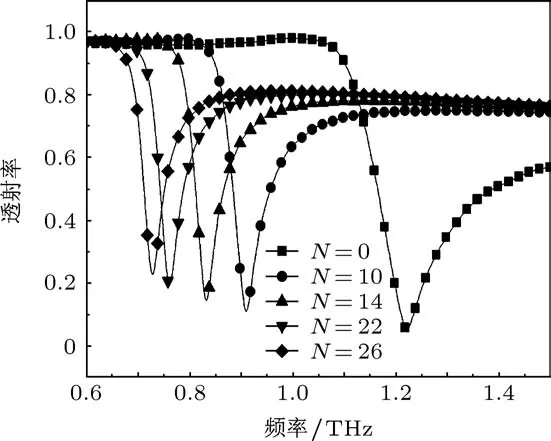
图4 短线数目N对谐振响应的影响

图5为含10支短线SRRs在谐振频率下的表面电流分布图.由图中圈注部分可看出，当SRRs产生磁谐振时，大小环金属短线处产生强烈的表面感应电流，且电流方向相反，说明大量异性电荷在此聚集，形成电容.

对于SRRs结构，金属线产生电感，大小环开口及两环间隙产生电容，当电磁波入射到磁谐振器上时，入射电磁波的磁场会在其上产生磁感应电流，从而形成LC谐振回路.因此SRRs的两环开口及间隙处结构参数对其谐振响应有着至关重要的作用.根据文献[9]，SRRs的磁谐振频率可近似由以下公式给出：

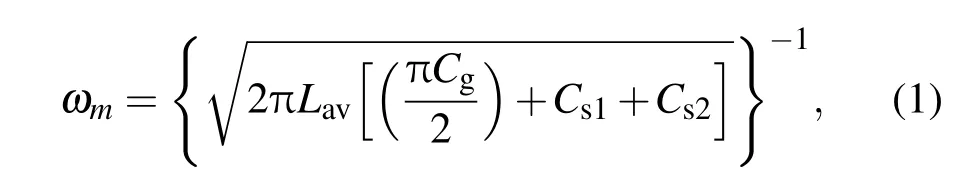
其中，Lav为金属环平均电感值，Cs1，Cs2分别为外环及内环开口处的电容值，Cg则为两环间隙处的电容.当SRRs两环间加有金属线并发生磁谐振时，两环间电容Cg增大，根据(1)式，两环间电容值Cg增大会导致谐振频率降低.因此，在SRRs两环间加入金属短线会使谐振频率降低.

图5 含10支短线SRRs的表面电流分布

2.3 金属短线结构参数对谐振频率的影响

为研究金属短线结构参数对SRRs谐振频率的影响，以短线数目N=10的SRRs单元为研究模型，短线长度Lx=3µm，宽度Wx=2µm，间距Gx=0.5µm.分别改变三项中的一项，保持其他两项不变，得出短线结构对谐振的影响，见图6—8.

保持金属短线的宽度Wx与间距Gx不变，当长度Lx由1.5µm增加到3µm时，SRRs的谐振频率由1.15 THz下降至0.91 THz，呈现红移，降幅为20.87%.

保持金属短线的长度Lx与间距Gx不变，改变Wx，SRRs的谐振频率随Wx的增加近似呈线性下降.当Wx由1.0µm增加到2.5µm时，谐振频率由0.94 THz下降至0.89 THz，呈现红移，降幅近5.32%.

保持金属短线的长度Lx与宽度Wx不变，当间距Gx由0.3µm增加到0.9µm时，SRRs的谐振频率由0.85 THz增大至0.94 THz，呈现蓝移，增幅为10.59%.同时，需要注意的是，随着Gx的增大，即金属短线的排布更为稀疏，谐振频率的变化程度也在逐渐减弱，Gx对谐振频率的影响不断减小.

图6 短线长度Lx对谐振响应的影响

图7 短线宽度Wx对谐振响应的影响

图8 短线间隙距离Gx对谐振响应的影响

总体上讲，对于加有金属短线的SRRs结构单元，其谐振频率随着Lx，Wx的增大及Gx的减小而不断向低频移动.这是因为，Lx，Wx的增大及Gx的减小，意味着金属短线的排布更加紧密，两金属环间距也同时减小，导致两环之间的电容值Cg增大，从而使谐振频率降低.

2.4 添加金属短线对减小器件尺寸的意义

对于SRRs结构，其单元尺寸是影响谐振频率的首要因素[12].以图2(a)所描述的传统SRRs结构为模型，通过改变边长L，其他参数保持不变，来研究单元尺寸与谐振频率的关系，具体结果见图9.

图9 外环边长L对谐振频率的影响

由图可见，随着单元尺寸的增大，SRRs的谐振频率不断降低.当外环边长由30µm增加至43µm时，谐振频率由1.22 THz降至0.67 THz.与含有26支金属短线的新型SRRs相比，要使两种结构单元的谐振频率相同，即0.72 THz，加有金属短线的新型SRRs的外环边长L仅需30µm，而传统SRRs的外环边长L则要增大至41µm，边长增大36.67%，单元面积增大86.78%.由此看出，通过在SRRs的两环间加入金属短线，可有效减小器件尺寸.

2.5 介质基底对谐振响应的影响

以上内容均为SRRs结构在真空中所得的模拟结果，忽略了介质基底的存在.实际上，介质基底因其介电常数、损耗及厚度的不同，也会对SRRs结构的谐振响应产生一定的影响，以下研究由介质基底所造成的影响.

以含有10支金属短线的SRRs结构为研究模型，金属为铜，厚度为3µm.基底材料为氧化铝，介电常数为9.9，损耗角正切值为0.0001.仿真时边界条件不变，电磁波沿x方向入射，电场沿y方向，磁场沿z方向.具体如图10所示.

图 11(a)—(d)分别为当基底厚度是 50，100，200和300µm时的S21曲线图.由图看出，基底的存在改变了SRRs的谐振频率，由无基底时的0.9 THz左右降至0.5 THz左右.当基底厚度从50µm增加至300µm时，谐振频率由0.494 THz升高至0.514 THz，但谐振强度却有较大的减弱.所以说，基底材料的介电常数将主要影响SRRs的谐振频率，而厚度主要影响其谐振强度.

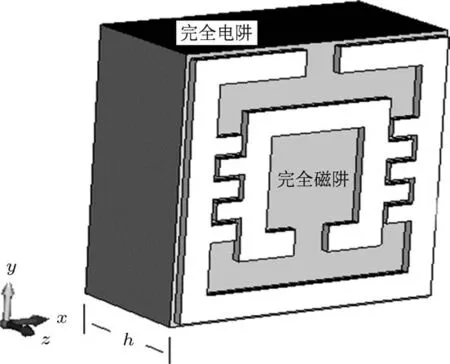
图10 含有介质基底SRRs的仿真边界条件

现研究当存在介质基板时，金属短线对谐振频率的影响.如图12所示，设基板依旧为氧化铝材料，厚度h=300µm，金属结构的参数同图1所示模型一致.当SRRs结构无金属短线，即N=0，谐振频率为0.684 THz;当N增加至26时，谐振频率大幅度下降，变为0.362 THz，降幅达47.08%.若以传统方式，即增大外环尺寸L的方式来降低谐振频率，使无金属短线的SRRs结构在0.362 THz发生谐振，如图13，L则应增大为44µm，长度增幅46.67%，器件面积增幅115.11%.因此，介质基板的存在虽然减弱了SRRs结构的谐振强度，但并不影响金属短线对减小器件尺寸方面的作用.

3 结论

本文通过在传统SRRs结构中引入金属短线，设计了新的磁谐振单元，并数值仿真了该新型谐振单元在太赫兹波段的谐振行为，分析研究了金属短线和介质基底的存在对SRRs谐振响应的影响.结果表明，谐振频率随着金属短线数目的增多而降低，且当短线数目为26时，磁谐振频率由1.22 THz下降至0.72 THz，降幅达到40.98%.此外，谐振频率也会随着金属短线长度Lx，宽度Wx的增加及间距Gx的减小而降低.最后，通过与传统SRRs结构相比较，证明了有短线的新型SRRs结构在器件小型化方面的显著优势.加入介质基底的仿真结果也表明，介质基底也不会影响到金属短线对减小器件尺寸方面的作用.相关的研究工作对于新型负磁导率材料及新型左手材料的设计具有重要的现实意义，并为太赫兹波段的器件设计工作提供了有意义的参考.

感谢空军工程大学理学院屈绍波教授和王甲富老师.

图11 不同厚度基底对谐振响应的影响

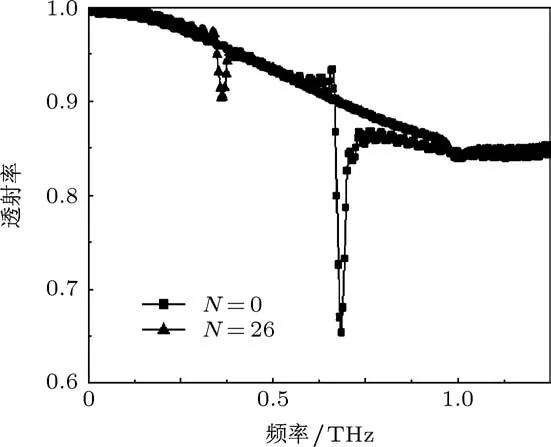
图12 h=300µm时不同数目短线的谐振响应

图13 h=300µm时L对谐振频率的影响

[1]Yen T J，Padilla W J，Fang N，Vier D C，Smith D R，Pendry J B，Basov D N，Zhang X 2004 Science 303 1494

[2]Sun Y Z，Ran L X，Peng L，Wang W G，Li T，Zhao X，Chen Q L 2009 Chin.Phys.B 18 174

[3]Ma H，Qu S B，Xu Z，Zhang J Q，Wang J F 2009 Chin.Phys.B 18 1025

[4]Veselago V G 1968 Soviet Phys.Usp.10 509

[5]Pendry J B，Holden A J，Stewart W J，Yongs I 1996 Phys.Rev.Lett.76 4773

[6]Pendry J B，Holden A J，Robbins D J，Stewart W J 1999 IEEE.Trans.Microwave Theor.Tech.47 2075

[7]Shelby R A，Smith D R，Schultz S 2001 Science 292 77

[8]Yao J Q，Yang P F，Bing P B，Di Z G 2011 Laser&Infrared 41 825(in Chinese)[姚建铨，杨鹏飞，邴丕彬，邸支刚2011激光与红外41 825]

[9]Radkovskaya A，Shamonin M，Stevens C J，Faulkner G，Edwards D J，Shamonina E，Solymar L 2005 Microwave Opt.Technol.Lett.46 473

[10]Aydin K，Bulu I，Guven K，Kafesaki M，Soukoulis C M，Ozbay E 2005 New J.Phys.7 168

[11]Labidi M，Tahar J B，Choubani F 2011 Opt.Express 19 733

[12]Wu J F，Sun M Z，Zhang C M 2009 Acta Phys.Sin.58 3844(in Chinese)[吴俊芳，孙明昭，张淳民2009物理学报58 3844]