粉末燃料高效装填技术研究①

杨晋朝，夏智勋，胡建新，孔龙飞

(国防科技大学高超声速冲压发动机技术重点实验室，长沙 410073)

0 引言

粉末燃料冲压发动机是一种新概念冲压发动机，它使用金属粉末为燃料、冲压空气为氧化剂和工质。具有比冲高、能量密度大、结构简单、燃烧产物稳定、燃料存储和使用过程中安全性高、燃料流量可主动调节等优点，在未来超声速导弹设计中受到广泛关注［1－2］。

粉末燃料冲压发动机使用高能量密度的固体颗粒(镁、铝、硼、碳等)作为燃料，理论体积比冲高。但由于粉末燃料的装填率不可能达到100%，所以发动机的实际体积比冲比理论体积比冲要低。为了使粉末燃料高效燃烧，发动机中使用的粉末燃料粒径都较小，在微米级以下。理论与实践都表明，颗粒越小，颗粒团聚、颗粒表面吸附作用越明显，松装密度越低［3］，这都使粉末燃料的装填率不能达到较高水平。在文献［4］中粉末燃料装填率只达到了37%，文献［2，5］也只达到了40%。因此，导致粉末燃料的体积热值降低很多。在装填率为40%的情况下，Mg粉末燃料的体积热值为17.3 kJ/cm3，而煤油和铝镁贫氧推进剂(组分为:20%Al，20%Mg，40%AP，20%HTPB)的体积热值分别为33.84 kJ/cm3和 33.26 kJ/cm3，可见，虽然 Mg的质量热值很高，但Mg粉末燃料的体积热值与煤油和铝镁贫氧推进剂相比处于劣势;燃烧热值更高的Al粉末燃料的体积热值(33.6 kJ/cm3)与这两者相比，也无优势可言［1］。

因此，要体现粉末燃料冲压发动机体积比冲高的优越性，必须提高粉末燃料的装填率，进而使其拥有较高的体积比冲。本文在对理想球形颗粒和非理想颗粒堆积理论全面系统分析的基础上，提出了理想的最紧密装填理论，并最终提出了一种简单有效的粉末燃料高效装填方法。

1 理想球形颗粒堆积理论

1.1 等径球体的有规则堆积

研究单一粒径理想球形颗粒的堆积特性是理解粉体堆积的基础。理想球形颗粒是指颗粒都是球形且表面光滑、不存在对相互移动有干扰作用的摩擦力和吸附力等。单一粒径球形颗粒规则排列的堆积参数如表1所示，其中立方体、体心立方、面心立方、六方最紧密堆积是4种典型的规则排列形式，见图1～图4。

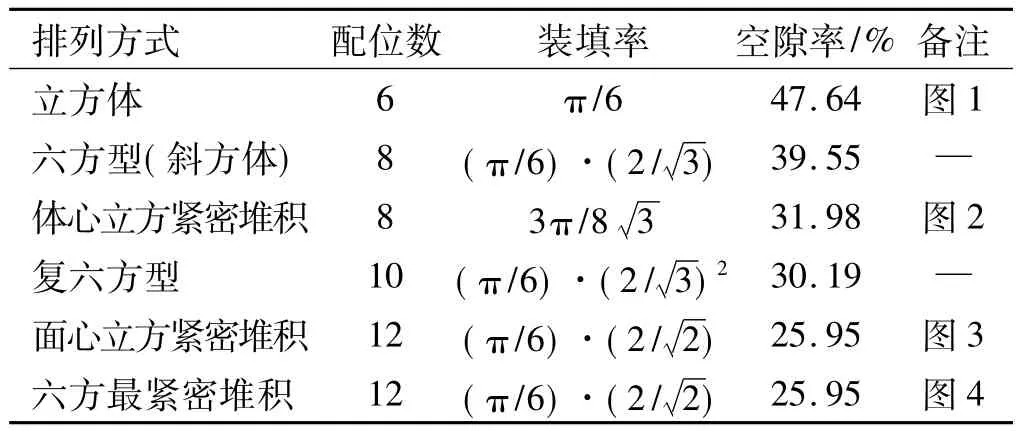
表1 单一粒径理想球形颗粒的堆积参数Table 1 Packing parameters of mono-disperse spherical particles

图1 立方体堆积Fig.1 Cubic packing

图2 体心立方紧密堆积Fig.2 Body-centered cubic close packing

图3 面心立方紧密堆积Fig.3 Face-centered cubic close packing

图4 六方最紧密堆积Fig.4 Hexagonal closest packing

由表1和图1～图4可知，配位数越大，其堆积密度越大。单一粒径理想球形颗粒装填密度最大的排列形式是面心立方紧密堆积和六方最紧密堆积，装填密度最小的排列形式是立方体堆积。在实际堆积中，颗粒的堆积一定是多种堆积形式的组合。所以，单一粒径粉体的装填率在π/6和(π/6)之间，其值与颗粒排列形式有关而与粒径大小无关。

1.2 异径球体的有规则堆积

当不同粒径的颗粒混合装填时，能达到更大的装填率。以六方最紧密堆积为例，根据Horsfield的六方最紧密堆积理论，6个球围成正八面体空隙，4个球围成正四面体空隙。六方最紧密堆积中基本的直径球称为1次球(半径r1)，填入正八面体空隙中的最大球称为2次球(半径r2)，填入正四面体空隙中的最大球称为3次球(半径r3);其后，再填入4次球(半径r4)，5次球(半径r5);最后，以极小的等径球填入残余的空隙中，这样就构成最紧密的堆积［6］。各次球径及装填率计算结果列于表2。

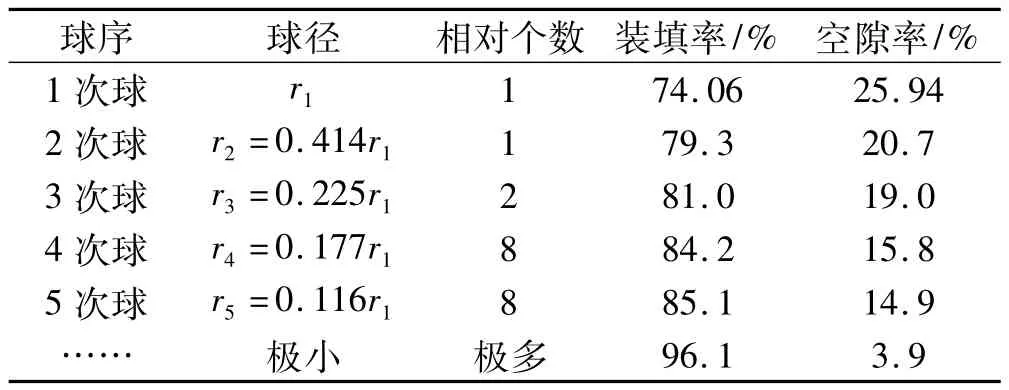
表2 六方紧密堆积的填充粒径与空隙率Table 2 Filling particles and voidages of hexagonal closest packing

同样，对于立方体堆积、斜方体堆积及体心立方紧密堆积等有规则排列，异径球多级填充也会使空隙率逐渐减小，直至最小。

1.3 等径球体的随意堆积

粉体在实际堆积中不可能完全是一种有规则的排列，而是多种排列方式的混合。Smith等通过实验，获得5种空隙率不同的等径球堆积配位数分布规律与平均空隙率及平均配位数的关系。假定堆积模型为立方堆积和六方最紧密堆积的混合，得到平均配位数和空隙率的关系式。

平均空隙率:

平均配位数:

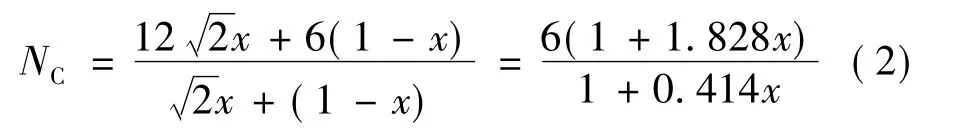
式中 x为六方最紧密堆积的比例数。

假设堆积模型为立方堆积和六方最紧密堆积的等比例混合，则x=0.5，用上述公式求得平均空隙率ε=36.8%，即装填率为63.2%。大量的实践证明，实际物料堆积中，装填率接近常数62%［3］。这说明该理论假设与实际情况比较相符。等径球体随意堆积空隙体积分数K是空隙体积含量与固体物质体积含量的比值，其计算式如下:

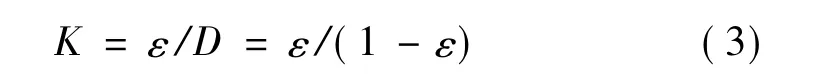
式中 ε为等径理想球形颗粒粉体的空隙率;D为粉体的装填率。

由于等径球体随意堆积的装填率接近常数0.62，所以等径球体粉体的K约为常数0.6。

1.4 异径球体的随意堆积

粉体一般并非由单一粒径的颗粒组成，而是由粗细颗粒混合而成。假设粉体由粗细两组分混合组成，则由粗细颗粒的粒径大小及含量比例的不同，可分为以下 3 种类型［7－8］。

第1种类型:细粉刚好能填满粗粉的间隙，混合粉体的空隙含量等于粗粉空隙体积含量减去细粉固体物质体积含量，如图5(a)所示。空隙体积分数为

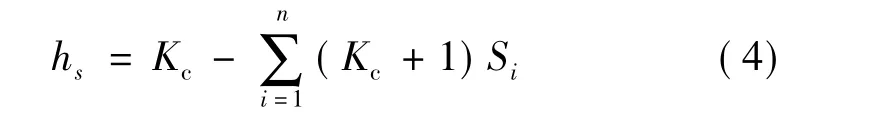
式中 Kc为粗粉空隙体积分数;Si为i粒级所占整个固体体积分数;n为粒级组分数。

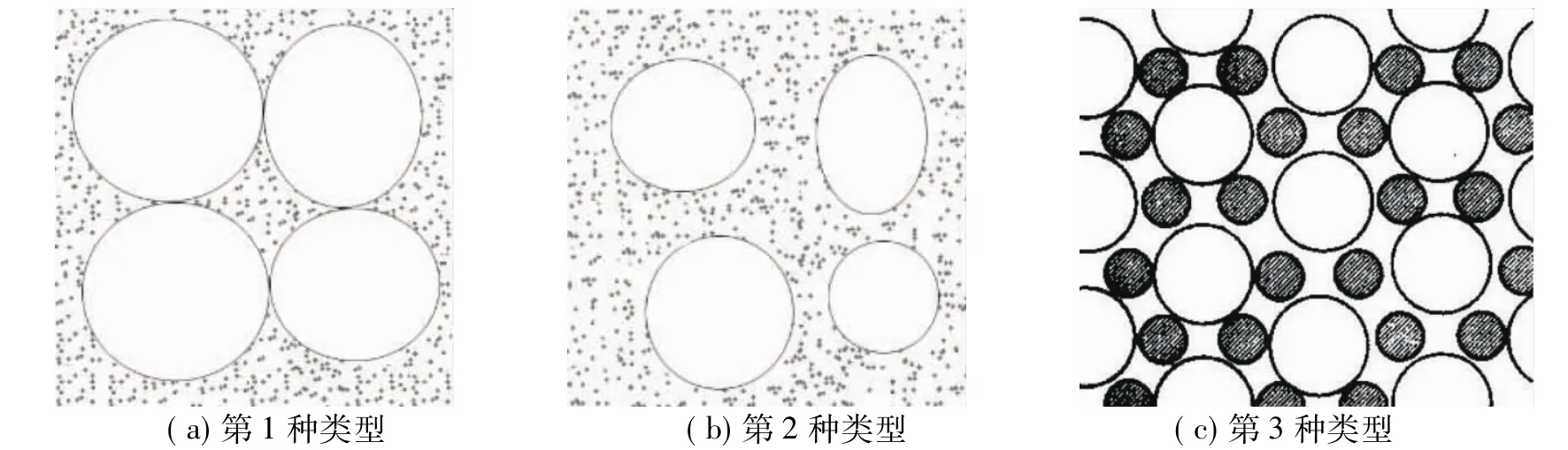
图5 异径球随意堆积的3种类型Fig.5 Three random packing types of multi-disperse particles

第2种类型:细粉分数大于粗粉空隙体积含量，粗颗粒被细颗粒挤开，好像“漂浮”在细粉中，混合粉体总体积也因此相应地扩大。混合粉体空隙含量等于细粉空隙体积含量，如图5(b)所示。空隙体积分数为

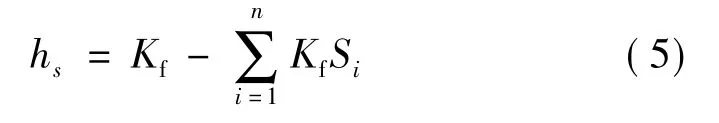
式中 Kf为细粉空隙体积分数。

第3种类型:由于细粉颗粒尺寸比例和几何形状不合适，不能填入粗颗粒间隙中。由于这种“颗粒干扰作用”增大了总体积量，也提高了空隙体积分数，如图5(c)所示。空隙体积分数为

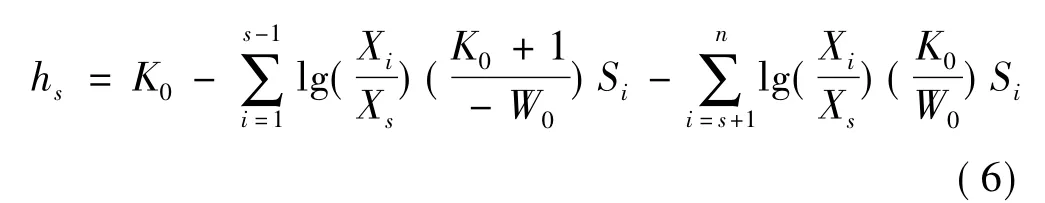
式中 K0为基础颗粒空隙体积分数;Xi为第i粒级的粒度;Xs为第s粒级的粒度;W0为颗粒干扰宽度，可表示为W0=lg(X0/Xw)，X0为基础颗粒粒度，Xw为极限颗粒粒度，是指刚好没有颗粒干扰作用的粒度。

在计算多粒级混合粉体孔隙体积分数时，极限颗粒粒度为除基础颗粒以外的任一粒级粒度。

由式(4)～式(6)可知，异径球体堆积的空隙体积分数必小于等径球体堆积的空隙体积分数，也即异径球体堆积装填率比等径球体堆积有更高的装填率。

综上，对理想球形颗粒的堆积规律有如下结论:

(1)相同粒径或相同粒径比的球形颗粒排列时，空隙率与其粒径的大小无关，仅与排列方式有关。

(2)排列方式相同时，多级配粒径球体的空隙率小于单一粒径球体的空隙率;并且级数越多，粉体的空隙率越小。

(3)颗粒堆在紧密排列的情况下，颗粒排列方式不是单一的，而是多种密排方式的混合。

2 非理想颗粒堆积

2.1 颗粒的干扰和干涉作用

实际粉末燃料都是不规则的，颗粒之间存在各种相互干扰，阻碍其自由移动。例如，细颗粒的几何尺寸不合适，几何形状不规则，不能恰好填入粗颗粒的空隙中，这时会将粗颗粒架开。另外，对混合粉体总体积的影响不仅是粗细颗粒的粒径比，更主要是它们的含量比例。若细颗粒含量太少，在粗颗粒之间必然留有未被填满的空隙;反之，所有粗颗粒的空隙都被填满后，剩余的细颗粒会将粗颗粒挤开。粗颗粒的外表面也不会是完全光滑的，对颗粒的自由滑动会起阻碍作用，干扰其有序排列。所以，在粗颗粒周围的细小颗粒往往不能紧密排列，留有较多空隙，这就是所谓的壁面效应［3］。细颗粒之间还存在相互吸附力，包括范德华力、静电力等，细粉末形成拱桥和互相粘附，妨碍了颗粒的相互移动。

20 世纪 30 年代，美国 Weymouth C A G［9］提出了颗粒干涉理论，1955年Williams提出了计算间断颗粒级配的干涉理论，该理论的要点为小颗粒的平均直径D2加上吸附层应小于平均粒径为D1的大颗粒的间隙，否则小颗粒会把大颗粒挤开，导致粉体的堆积密度下降，这就是所谓的“干涉作用”。计算表明，单级球颗粒在六方最紧密排列的情况下，可自由通过其间隙(不发生干涉作用)的小颗粒与大颗粒的关系为r=0.154 7R，在4个相邻的大颗粒中，其间隙可容纳小颗粒的最大半径为0.224 7R，如图6所示。单级球颗粒在简单立方排列的情况下，可自由通过其间隙(不发生干涉作用)的小颗粒与大颗粒的关系为 r=0.414 2R，在4个相邻的大颗粒中，其间隙可容纳小颗粒的最大半径为0.722 0R，如图7所示。

为研究颗粒之间的干扰和干涉作用，本文选取了9种粉末燃料作为实验样本，如表3所示。以2#、8#样本为例，详细说明颗粒之间的干扰和干涉作用。图8为2#、8#样本的扫描电镜照片。

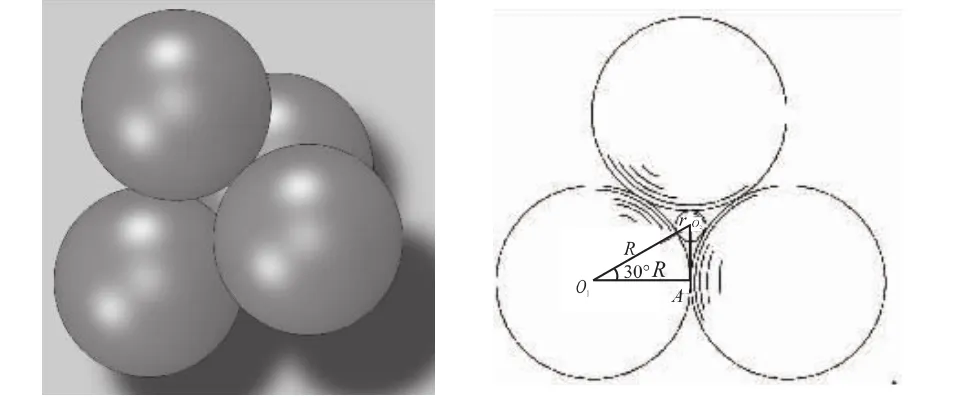
图6 六方最紧密堆积时大小颗粒粒径比Fig.6 Diameter ratio of big/small particles in hexagonal closest packing

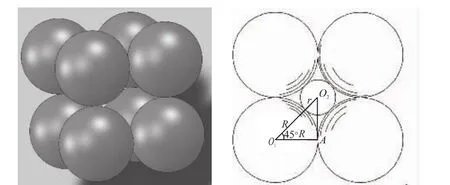
图7 立方体堆积时大小颗粒粒径比Fig.7 Diameter ratio of big/small particles in cubic packing

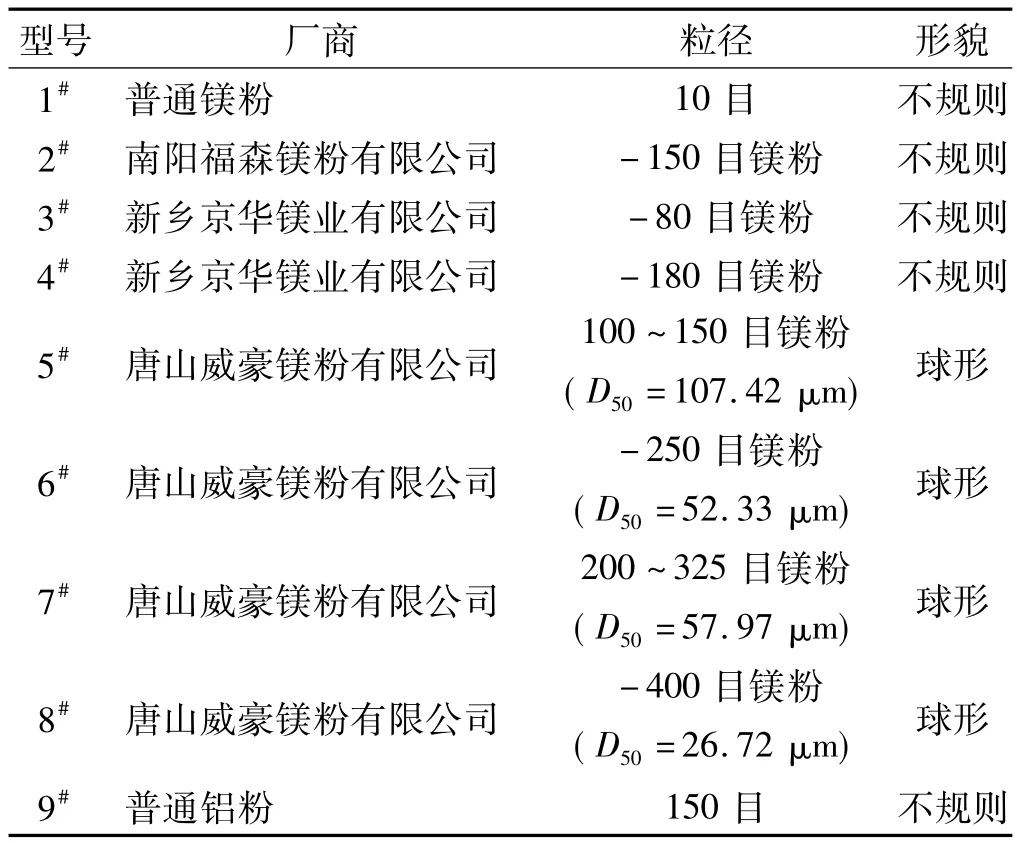
表3 实验样本Table 3 The samples for experiment

图8 2#、8#样本的扫描电镜照片Fig.8 SEM photos of 2#and 8#samples

由图8(a)、(b)可看出，2#粉末颗粒形状极不规则，且颗粒大小不均匀，颗粒表面也不光滑，颗粒之间相互干涉严重，小颗粒不能进入大颗粒之间的空隙内，从而粉体总的空隙率较大。在 1#、3#、4#、9#粉末的扫描电镜照片中也发现了此类干涉现象。由图8(c)、(d)可看出，8#粉末颗粒的球形度较好，但颗粒大小不均匀，大小颗粒相差较大。细小颗粒的吸附力不可忽略，如两图中圆圈内颗粒，在吸附力作用下，小颗粒可克服重力影响附着在大颗粒表面上。在5#～7#镁粉扫描电镜照片中也发现了细小颗粒的吸附现象。在图8(d)中还可清晰地看出，颗粒表面并非完全光滑。这都说明在实际粉体堆积中，干扰和干涉作用是不可避免的。

2.2 样本粉体的松装装填率

粉末燃料冲压发动机中的粉末燃料是在气流拖曳力的作用下从供应系统中流出，而振实状态的粉末燃料由于相互之间作用力较大，不易于流化。所以，目前粉末燃料供应系统中的粉末燃料是松装装填的。文中研究也主要围绕粉末燃料的松装装填率开展，共选取了9种粉末作为实验样本(见表3，其SEM照片如图9所示)，测量其松装密度，称量工具使用上海浦春计量仪器有限公司生产的精密电子天平(精度为0.01 g)。

图9 9种样本的扫描电镜照片Fig.9 SEM photos of nine samples

由图9可看出，1#～4#、9#样本颗粒的形状极不规则，球形度很差，颗粒大小也不均匀。5#～8#样本颗粒的形状球形度很好，表面光滑度也很好，其中5#的颗粒表面光滑度最好。5#颗粒大小较均匀，而6#～8#粒径小的颗粒含量相对较多。实验测得这9种样本的松装状态装填率如图10所示。

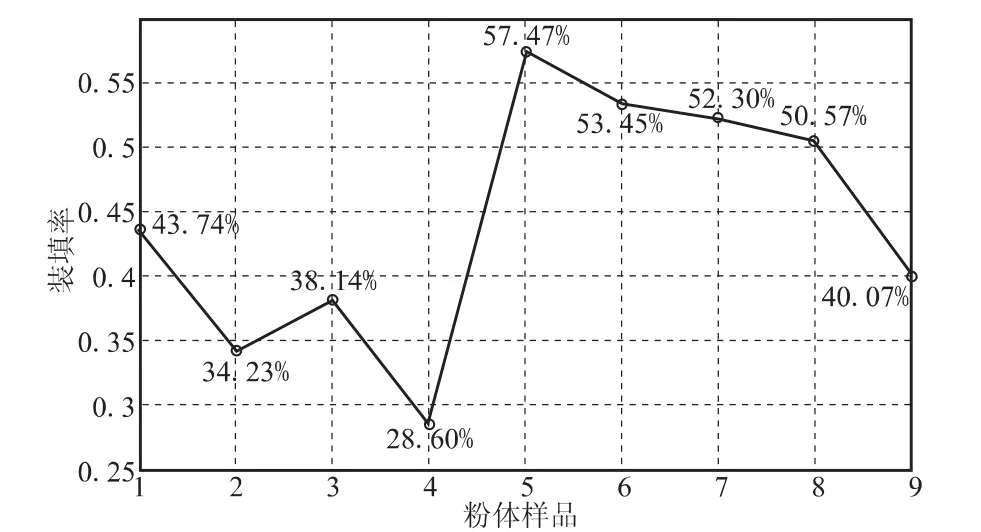
图10 样本的松装装填率Fig.10 Loose packing ratio of various samples

由图10可知，球形颗粒粉体(5#～8#)的松装装填率整体高于不规则颗粒粉体(1#～4#、9#)的松装装填率;而同一类型的粉体，大颗粒粉体的松装装填率又高于小颗粒粉体的松装装填率;但所有粉体的装填率都小于理想等径颗粒粉体的装填率62%。这说明实际粉体中颗粒形状越不规则，颗粒粒径越小，则粉体的装填率越低。与理想粉体不同，颗粒间的干扰干涉作用对粉体装填率的影响较大，且不可避免。由图10可知，5#样本球形度最好，表面最光滑，颗粒较大，所以颗粒间干扰作用较小，其松装装填率最大;而4#样本颗粒很不规则，颗粒也较小，所以颗粒间干扰作用较大，其松装装填率最小。

综上所述，实际粉体颗粒间的干扰和干涉作用阻碍颗粒形成最紧密堆积，使粉体的空隙率变大。颗粒形状越规则，粉体的松装装填率越大;颗粒越细小，颗粒的相互作用力越大，粉体的松装装填率越小。

3 粉末燃料的高效装填

由以上分析，为提高颗粒的装填密度，要尽量使用球形度好的颗粒，且必须采用多级配装填。而在多级配装填中，需解决2个主要问题:一是颗粒级数及粒径比的确定;二是各级颗粒含量比例的确定。

3.1 高效装填理论

实际粉体堆积不可能是颗粒的有规则堆积，本文假设一种最紧密堆积理论，其几何模型如图11所示。其中(a)表示各种不同粒级的颗粒分层装填的情况;(b)表示各个粒级的颗粒混合后按最紧密堆积的理想情况;(c)表示各粒级颗粒混合后的实际情况。

在n级颗粒分层装填时，粉体总体积如图11(a)所示。理想的最紧密装填方法如下:在一个固定容器内(如一个单位体积的容器)，先用大尺寸的一号颗粒(粒径为d1)充满容器，再用粒度远小于一号颗粒的二号粒子(粒径为d2)充满一号颗粒的空隙;然后，再用远小于二号粒子的三号粒子充满二号颗粒的空隙，……。如此填充下去，可使装填率达到最大(约为1，如图11(b)所示)，此时的装填密度趋近该物质的真密度。现实中不可能做到如此紧密的装填，实际的混合装填效果如图11(c)所示。

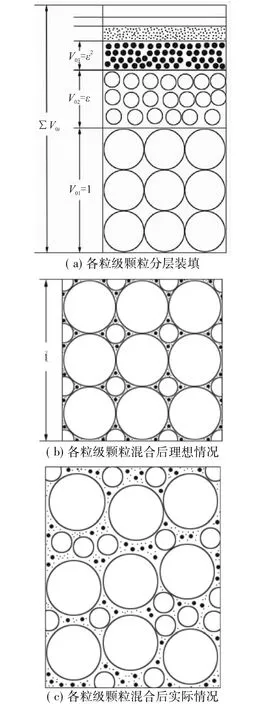
图11 最紧密装填的几何模型Fig.11 Geometric model of the closest packing

虽然实际中高效装填为图11(c)所示效果，但图11(b)所示的最紧密装填，为高效装填提供了一种方法，最紧密装填理论的假设如下:

(1)各级粒子的空隙率均为ε;

(2)在装填后，各级粒子本身的空隙率不变;

(3)各级颗粒为均匀、表面光滑的球形颗粒。

该理论认为有无穷级粒子，次级粒子直径远小于上一级粒子直径。在这种理想的假设下，各级颗粒的装填情况见表4。

表4 各级颗粒的装填情况Table 4 Packing ratios of multi-grade particles

粉体的初始装填率(D0=1－ε)不同，粒级数n与理论上能达到的最大装填率D的关系也不相同，图12为不同初始装填率的粉体粒级数与总装填率的关系曲线。由图12可知，初始装填率越大，多粒级粉体达到同一最紧密堆积密度所需的粒级组分数越小。但所有曲线都在n≤3时上升很快，而n＞3时上升趋势减缓，这就是说，三级以下的级配装填对提高粉体的装填密度是非常有效的，而三级以上的级配装填对提高粉体的装填密度已不是很明显。

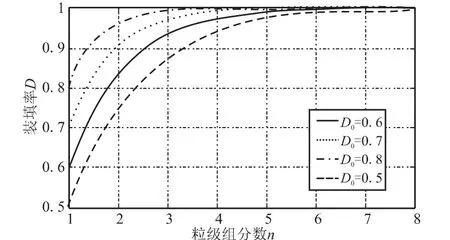
图12 多级混合粉体中粒级组分数与装填率的关系Fig.12 Relationship between packing ratio and size fraction of multi-grade spherical particles

高效装填方法:

(1)各级颗粒粒径比的确定

最紧密装填理论要求次级粒子直径远小于上一级粒子直径，而在实际中却无法满足“远小于”的要求。根据2.1节中讨论，在六方最紧密排列的情况下，可自由通过其间隙(不发生干涉作用)的小颗粒与大颗粒的关系为r=0.154 7R，即 R/r=6.46。据此，认为相邻两级的颗粒粒径比以大于6.5为宜。

(2)各级颗粒质量百分数的确定

各级颗粒体积百分数的确定是颗粒级配的首要问题。因为对于同一种材料(其密度相同)，其体积分数也就是质量分数。因此，可根据各级颗粒的空隙率直接计算其最佳配比。

例如，各级颗粒的真实体积比体积比即为质量比，由表4可知:

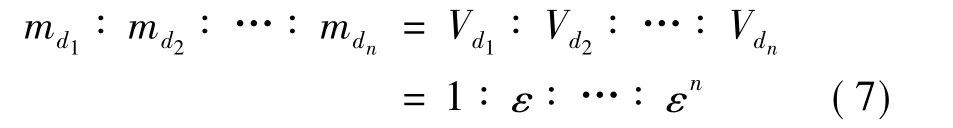
据此可确定各级颗粒质量百分数。

在实际混合装填中，若各级颗粒的空隙率不相等，则

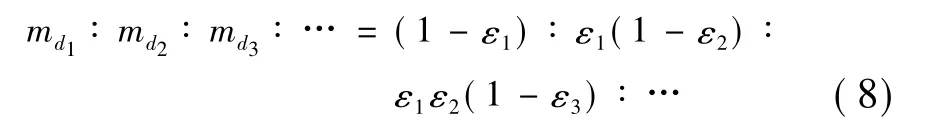
式中 ε1、ε2、ε3分别为1级、2级、3级颗粒的初始空隙率。

(3)颗粒级数的确定

由表4和图12可知，n级装填后所余下的空隙为εn，若 ε=0.4，则当组分数 n＜3时，空隙率下降明显，n＞3时，空隙率下降就不明显了;从另一角度，颗粒级数越多，则要求最大与最小颗粒粒径比越大，否则不能达到混合密度较大的目的。综合这两方面考虑，实际中常采用二级或三级颗粒级配。

3.2 粉末燃料的高效装填

由高效装填理论，装填颗粒应尽量选用球形度好且表面光滑的颗粒，再考虑粒径比的要求，确定了二级配混合装填的方案。在球形度好的样本中，选取5#和8#样本作为级配粉末，使用BT-9300H型激光粒度分布仪(丹东市百特仪器有限公司生产)，检测这2种粉末的粒度分布，测试结果如图13所示。

由图13可看出，8#样本颗粒粒度多集中在20～40 μm之间，5#样本颗粒粒度多集中在90～200 μm 之间(图13(b)中红线第二个峰，仅表示145～180 μm颗粒的区间百分含量略高于与其相临粒径的颗粒的区间百分含量)，这2种样本基本能满足级配装填中相邻颗粒R/r＞6.5的要求。再由式(8)和图10确定5#和8#样本的质量比:

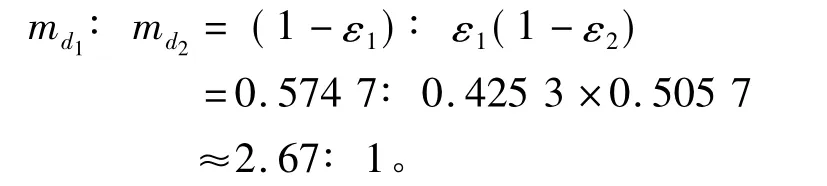
将质量比为2.67的5#、8#样本混合均匀，用电子天平(精度0.01 g)测量其松装密度。取3次测量值的算术平均值为混合粉末的松装密度值。实验得出此配比情况下粉体的松装装填率为67.16%，比单级装填情况下松装装填率最高的5#粉末提高了将近10%。为了验证此方法的可靠性，改变2种样本的配比进行了对比实验，实验结果如表5所示。表5中，φ为装填率，φ+ε=1。

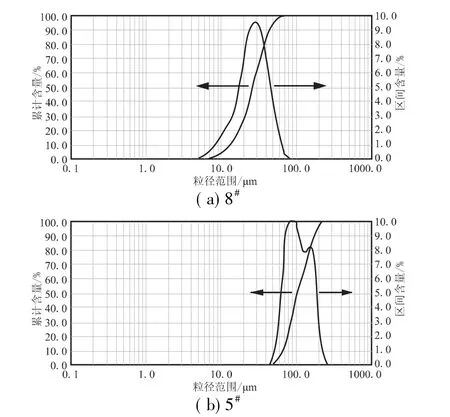
图13 8#和5#样本粒度测试结果Fig.13 Test results of particle size of 8#and 5#sample

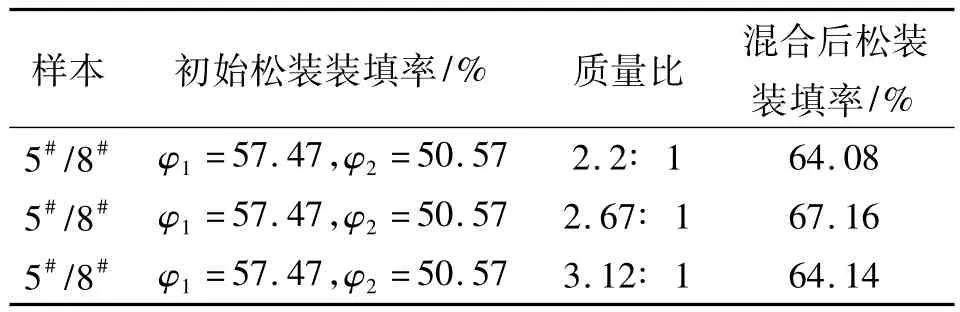
表5 大小颗粒不同配比实验结果Table 5 Experimental results of various mass ratios of big/small particles

由表5可知，5#、8#样本的质量比变大或变小后，粉体混合后的松装装填率都有所下降，这说明本高效装填方法确定的不同粒级含量比例是最佳的，以此方法来提高粉末燃料的装填密度是可行的。

4 结论

(1)理想球形颗粒堆积时，空隙率与粒径大小无关，仅与排列方式有关;在排列方式相同情况下，多级配混合粒径装填会减小粉体的空隙率，且级数越多，粉体空隙率越小;颗粒在紧密堆积状态下，其排列方式不唯一，是多种密排形式的组合。

(2)实际粉体颗粒间的干扰和干涉作用必然存在，并阻碍颗粒形成最紧密堆积，使粉体的空隙率变大。颗粒形状越规则，粉体的松装装填率越大;颗粒越细，颗粒的相互作用力越大，粉体的松装装填率越小。

(3)提出一种粉末燃料的高效装填方法，即填料中上级颗粒与次级颗粒粒径之比应大于6.5;质量比满足式(8);颗粒级数采用二级或三级。通过实验验证，这种方法可将粉末燃料的松装密度提高近10%，是一种简单有效地提高粉末燃料装填率的方法。

［1］申慧君，夏智勋，胡建新，等.粉末燃料冲压发动机燃烧室两相流数值模拟［J］.固体火箭技术，2007，30(6):474.

［2］申慧君.粉末燃料冲压发动机关键技术探索与研究［D］.长沙:国防科技大学，2008.

［3］乔龄山.水泥堆积密度理论计算方法介绍［J］.水泥，2007(7):1.

［4］Miller T F，Walter J L，Kiely D H.A next-generation auv energy system based on aluminum-seawater combustion［C］//Proceedings of 2002 Workshop on Autonomous Underwater Vehicles.2002:111.

［5］韩超.粉末冲压发动机燃料供应系统研究［D］.长沙:国防科技大学，2006.

［6］王立久，刘慧.矿料级配设计理论的研究现状与发展趋势［J］.公路，2008(1):170.

［7］吴成宝，胡小芳，段百涛.粉体堆积密度的理论计算［J］.中国粉体技术，2009，15(5):76.

［8］Reschke T.Schriftenreihe der zementindustrie 62/2000［M］.Düsseldorf:Verlag Bau Technik GmbH，2000.

［9］Weymouth C A G.Effects of particle interference in mortars and concrete［J］.Rock Products，1933，25:26.