斜拉桥π型主梁恒载剪力滞效应

杨 健 李银斌 阮 欣

（1.贵州省交通规划勘察设计研究院股份有限公司 贵阳 550001；2.同济大学 上海 200092）

1 引言

大跨度斜拉桥中，结构自重在总荷载中所占的比重较大，为尽可能减轻自重，双索面混凝土斜拉桥主梁截面由箱型逐渐演变为带边主梁的肋板结构形式——π型主梁［1］。该截面形式能够有效降低自重，便于悬臂施工，且具有较好的承载性能，是一种极具竞争力的主梁形式，但其截面设计理论方面尚存在待研究和解决的问题。

因π型主梁梁肋与桥面板刚度不同，由腹板传递的剪力流在边缘上受拉要大一些，而向板内传递的过程中，由于桥面板发生剪切变形，拉应力会逐渐减小，故应力在桥面板横向上的分布是不均匀的，该不均匀特征称之为剪力滞效应。

π型梁在施工阶段可能发生正或负剪力滞效应，根据定义，若肋板处正应力大于初等梁理论的计算值，则称之为“正剪力滞”效应，若肋板处正应力小于初等梁理论的计算值，则称之为“负剪力滞”效应，π型主梁正负剪力滞效应见图1。

图1 正负剪力滞示意图

我国现行规范缺少对π型主梁剪力滞系数的相关规定，且大多数开展的研究采用增广位移法［2－4］等理论解析 方法或有限元法［5］对特定荷载情况下的箱梁进行研究，而少数针对多肋式梁桥［6］或者π型主梁［7］剪力滞系数的研究工作也仅针对特定荷载情况，不能考虑施工阶段中结构形式以及恒载效应多变的情况。

综上所述，研究并明确π型主梁在关键施工阶段下的剪力滞效应，对于设计是十分重要的。本文以某π型主梁斜拉桥为例，采用实体有限单元法，开展关键施工工况下主梁恒载剪力滞效应的相关研究工作，其结论及分析思路可为同类工程提供借鉴。

2 工程概述

贵州省某斜拉桥为3跨连续预应力混凝土斜拉桥，跨度组合为195m＋438m＋195m，交角90°，桥梁全长828m。桥面由两侧1.3m斜拉索区和21.5m行车道组成，全宽24.1m。桥面铺装为防水层＋10cm厚沥青混凝土，主梁采用C60高强混凝土。桥梁总体布置及横断面布置见图2、图3。

图2 桥梁总体布置图（单位：m）

图3 π型主梁横断面（单位：m）

3 有限元模型及分析说明

3.1 模型建立

采用大型通用有限元程序ANSYS建立全桥空间有限元模型，由于仅关注主梁空间应力状态，主梁采用空间实体单元Solid45模拟，而主塔则采用空间梁单元Beam188模拟。纵向预应力钢筋采用Link8单元模拟，斜拉索采用Link10单元模拟，斜拉索与主塔间以Beam4单元形成的刚臂进行连接，整体模型见图4。

图4 桥模型

3.2 计算工况

由于各施工阶段结构体系和荷载形式不同，对剪力滞影响也不相同，选取较为关键的最大双悬臂工况以及成桥工况进行恒载剪力滞系数分析，工况及说明见表1。

表1 计算工况说明

3.3 分析截面及关键点

计算选取次边跨跨中、边跨跨中、主塔根部、主跨四分点、主跨跨中等5个关键位置附近截面（避开横梁）进行研究分析，截面编号依次为1～5，位置见图5。

图5 截面编号

对于本桥，研究在主梁横截面上定义12个点（顶板A～G、底板H～L）来描述断面应力分布特性，各点在横断面上的相对位置见图6。

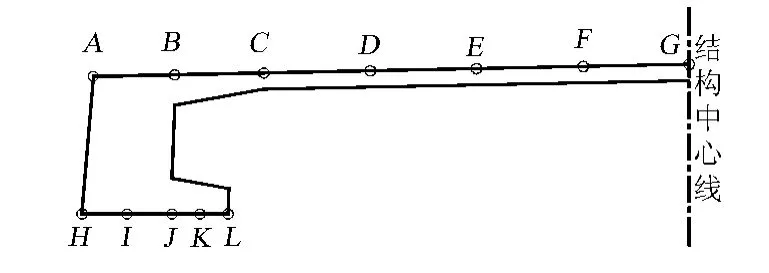
图6 剪力滞研究关键点

4 恒载剪力滞

4.1 剪力滞系数定义

剪力滞系数定义为考虑剪力滞效应所求得的正应力与按简单梁理论所求得的正应力比值。由于剪力滞效应仅引起截面正应力重分布，初等梁理论求得的正应力与平均正应力相差较小，本文以平均应力值代替初等梁理论值进行计算。以A点为例，剪力滞系数可描述为：

式中：σA为考虑剪力滞效应所求得的A点正应力；¯σs为平均应力值。

4.2 各截面应力分布

以4，5号截面为例，将各工况应力绘制于图7，因其桥面中心线对称，各工况仅示出一半。

图7 工况截面纵向应力分布图（单位：MPa，受压为负）

工况一为最大双悬臂工况，由于该工况下主跨跨中块段尚未施工，跨中截面即5号截面无应力数据。

4.3 剪力滞效应分析

斜拉桥主梁受自重均布力、索力竖向分力以及索力轴向分力综合作用，其应力状态较为复杂，正负剪力滞现象由施工索力状态以及边界支承条件决定，均有可能产生。据分析可知：

（1）1号截面剪力滞效应并不明显，上下缘应力分布较为均匀，这是因为本截面梁肋宽度相对较宽，桥面板较窄的缘故。

（2）2工况下2，3号截面均受负剪力滞影响，其中3号截面下缘因设置临时纵向支承，出现局部应力集中区域。

（3）4号截面受正剪力滞效应影响，梁肋处的正应力大于桥面板处正应力，但该效应较小，在工况一及工况二下，顶缘最大与最小正应力比值分别为1.05与1.08。

（4）5号截面在成桥后受负剪力滞效应影响，梁肋处正应力小于桥面板处正应力。

4.4 剪力滞系数分析

（1）工况一。根据有限元分析方法求解工况一关键点剪力滞系数，汇总见表2、表3。

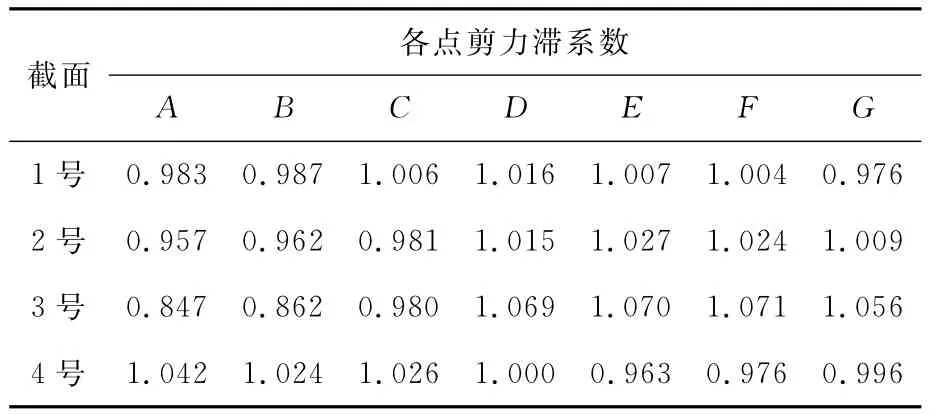
表2 工况一顶板关键点剪力滞系数

表3 工况一底板关键点剪力滞系数

根据工况一计算结果可以看出：①绝大多数计算点的剪力滞系数均在0.9到1.1之间；②3号截面顶A－G、底板H－L关键点剪力滞系数波动较大，顶板剪力滞系数最小为0.847（A点），最大为1.071（F点）。底板剪力滞系数最小不均匀系数为0.576（J点），最大为1.427（K 点），这是由于3号截面为塔根部主梁断面，在施工中设临时纵向支承引起局部应力集中的缘故。

（2）工况二。根据有限元分析方法求解工况二关键点剪力滞系数，汇总见表4、表5。

表4 工况二顶板关键点剪力滞系数

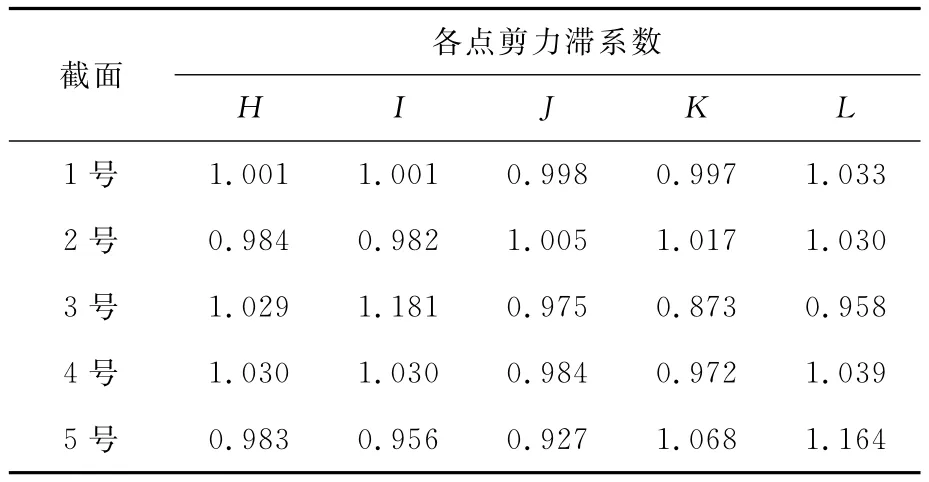
表5 工况二底板关键点剪力滞系数

根据工况二计算结果可以看出：①绝大多数计算点的剪力滞系数均在0.9～1.1之间；②3号截面底板H－L关键点剪力滞系数波动较大，底板剪力滞系数最小为0.873（K 点），最大为1.18（I点）；③5号截面底板L点的不均匀系数略大，为1.164，其余各点均在0.9～1.1之间。

4.5 对比分析及设计建议

出于设计中仅关注梁肋及桥面板最大剪力滞效应考虑，提取汇总各截面梁肋以及桥面板处的最大剪力滞系数进行分析，汇总见图8。

图8 各截面梁肋与桥面板剪力滞系数

根据梁肋及桥面板剪力滞系数分布规律得出：

（1）3号截面在工况一与工况二下的剪力滞系数差别较大，这是由于临时约束解除的缘故。

（2）梁肋上缘剪力滞系数大多数在0.9～1.0之间，3号截面略小于0.9，4号截面则略超出；设计中梁肋上缘的剪力滞系数可按1.0考虑。

（3）1，2，4号截面梁肋下缘剪力滞系数大多在1.0～1.1之间，设计中可按1.1考虑；工况一3号截面由于下缘局部应力集中，可根据工况二成桥工况选用，取为1.2；中跨跨中5号截面梁肋下缘最大剪力滞系数为1.164，也可偏安全按1.2考虑。

（4）工况一及工况二桥面板最大剪力滞系数均在1.016～1.071之间，可偏安全按1.1考虑。

5 结论

（1）剪力滞效应受截面特性内力状态以及支承边界影响，次边跨跨中、塔根、中跨跨中为负剪滞效应，中跨四分点为正剪滞效应。

（2）最大双悬臂工况及成桥工况下，除约束边界改变的3号截面剪力滞系数相差较大外，其余截面（除未浇筑的中跨跨中截面）剪力滞系数相差不大。

（3）梁肋上缘恒载剪力滞系数可取为1.0；梁肋下缘剪力滞系数，塔根处可取为1.2，其余截面可取为1.1；桥面板剪力滞系数可取为1.1。

［1］李 鑫.混凝土π型梁斜拉桥的温度场分析及温度效应研究［D］.长沙：长沙理工大学，2009.

［2］耿少波，石雪飞，阮 欣，等.增设广义位移下箱梁剪力滞效应的变分法［J］.同济大学学报，2010，38（9）：1276－1280.

［3］李小祥，石雪飞，阮 欣，等.低高度混凝土单箱单室宽箱梁剪力滞效应研究［J］.结构工程师，2008，24（2）：43－47.

［4］项海帆.高等桥梁结构理论［M］.北京：人民交通出版社，2001.

［5］程翔云.梁桥理论与计算［M］.北京：人民交通出版社，1998.

［6］秦绪喜.基于辛弹性力学的宽翼板T梁及箱梁剪力滞理论［D］.吉林：吉林大学，2009.

［7］万 臻.斜拉桥常用截面形式主梁的剪力滞效应研究［D］.成都：西南交通大学，2009.