自适应反馈单神经元模型混沌非线性电路实现设计研究

陈 军

（1.定西师范高等专科学校 物理与电子工程系，甘肃 定西 743000；2.武汉大学 电子信息学院，武汉 430072）

非线性电路在混沌的理论探索和应用研究中起着非常重要的角色，混沌电路有很大的现实意义和应用价值［1］.自蔡氏电路系统［2］认识以来，将混沌与电路这两个不同的领域联系起来，使混沌系统在数据加密、安全通信和优化计算等信号处理方面有很大的应用潜能［3］.在许多技术及工程应用领域有目的地产生和加强混沌行为已成为一个重大课题.

神经网络模型是以神经元的数学模型为基础来描述的.神经网络是一个高度非线性动力学系统.神经网络动力学特性已成为当前研究的焦点问题［4］.在各种不同类型的神经网络中混沌现象一直被受到观察和研究.例如，文献［5］对具有三细胞的神经网络混沌行为进行了研究；文献［6］描述了三神经元的Hopfield型的神经网络的混沌现象；文献［7］研究了具有外部激励的单细胞神经元禁忌学习的混沌行为；文献［8］对高维神经网络在外部正弦激励下的混沌现象进行了考察；文献［9］发现了迟滞神经网络能表现出混沌行为，对混沌吸引子及周期解共存性进行了探讨；文献［10］对混沌神经元同步及优化也有研究.特别是近年来神经元模型及混沌神经网络的电路实现［11－12］受到一些学者的关注.

本文研究了具有反馈的单神经元模型的非线性动力学行为的电路实现与设计方法，探讨了单神经元模型的两个共存吸引子到一个吸引子的变化等混沌现象，利用EWB［13］软件仿真验证了所设计的反馈单神经元模型电路的正确性.

1 具有自适应反馈突触的单神经元模型

本文所研究的神经元的动力学模型［4］方程为：

其中，p、q是正常数，外界输入正弦函数为I＝εsin（ωt＋φ）.这里，我们取激活函数f（x）为：

2 反馈突触神经模型电路实现设计与仿真

在研究文献［11－12，14－15］等的基础上，分别设计实现了激活函数的电路、反馈突触单神经元模型电路，并用运EWB软件对所设计电路进行了电路仿真实验，以下分别加以介绍.

2.1 激活函数电路的实现设计与仿真

激活函数（2）的功能由三个双曲正切函数的线性组合实现，而双曲正切函数可以通过双极性晶体管获得.由电路定律，对如图1 所示电路进行分析［16］.

图1 双曲正切函数基本电路Fig.1 Basic circuit of hyperbolic tangent function

这就是双曲正切函数模型的传输特性函数表达式.

在电路设计中，作者采用一个实现双曲正切函数f（x）＝tanh（x）功能的更加实用电路，称为模块单元电路［15］.

根据以上分析，激活函数（2）可由3个tanh（·）模块单元电路和线性电阻、电子集成运算放大器LF356等器件来实现，如图2所示为激活函数f（x）的电路图，为了叙述方便，我们称其为f（·）单元电路.

根据电路回路定律，对图2所示的电路进行分析，状态方程如下：

图2 f（·）单元电路图Fig.2 Unit circuit of f（·）

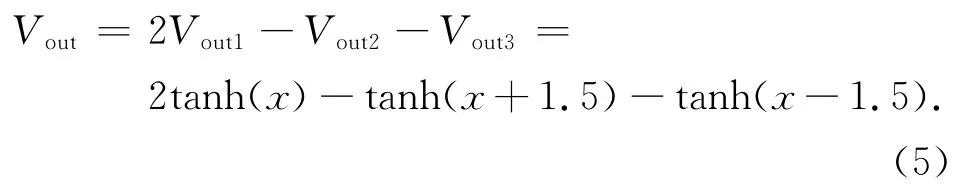
通过对比方程（5）与（2），表明作者所设计的f（x）单元电路能够实现反馈突触单神经元模型的激活函数.

2.2 反馈突触单神经元模型电路实现设计与仿真

对模型（1），设参数取值分别为［4］：τ＝1、p＝q＝5、ε＝0.3、ω＝2π、φ＝0或φ＝π，α取一系列不同的常数值.则模型（1）转化为：

在EWB软件环境下，为了将模型（6）通过电子电路实现，运用线性电阻、线性电容、电子集成运算放大器、乘法器AD633和f（·）单元电路等电子器件来设计实现，根据模型（6）和电路基本原理以及各个元件的特性，转换成相应电路元件，则其电路如图3所示.

图3 模型（1）的电路图Fig.3 Circuit of model（1）

电路中运算放大器LF356与线性电阻、电容搭配完成电路的加、减、微分及反相运算，乘法器用来实现非线性二次运算，f（·）单元电路实现激活函数（2）的功能，VS为外部输入正弦信号，其表达式为Vs＝－0.3sin（2πt＋φ）.电路中全部元器件均选用EWB中理想的虚拟电子元件.根据理想运算放大器的基本特性，由图3可推导出模型（6）的电路数学模型如下：

令u1＝u，u2＝s，则模型（6）和（7）等价.

在模型（1）中α＝1.4时，即对应于图3电路中，可变电阻Rw1＝Rw2＝R19＝14kΩ 的阻值情况，运用EWB 仿真软件，对设计电路进行仿真实验，其结果如图4、5所示，为混沌吸引子u（t）－s（t）相位图和t－u（t）波形图.图4中（a）为初值φ＝0时二维混沌吸引子的相平面图，（b）为当φ＝π时的相位图，可见此条件时系统出现2倍周期现象；图5中的（a）、（b）分别对应于初值φ＝0、π时ts（t）混沌吸引子的波形图.

图4 α＝1.4时u（t）－s（t）相位图Fig.4 u（t）－s（t）phase track chart atα＝1.4

图5 α＝1.4时t－s（t）波形图Fig.5 t－s（t）wave form atα＝1.4

在EWB仿真软件环境下，继续改变图3电路中的可变电阻，使Rw1＝Rw2＝R19大于16kΩ，两个分离的吸引子联结在一起，实现两个共存吸引子向一个相连吸引子转化的混沌现象.如图6所示为Rw1＝Rw2＝R19＝18kΩ 时即α＝1.8的二维混沌相连吸引的相平面图.

当α超过大约3.5时，它又分离成两个独立的吸引子.随着α的增加，其变成周期性轨道.当α＝5.5时即Rw1＝Rw2＝R19＝55kΩ，其对应于不同初值φ的仿真结果分别如图7（a）、（b）所示，为u（t）－s（t）的二维混沌吸引子的相平面图形，其结果都与文献的理论值相一致.

图6 α＝1.8时u（t）－s（t）相位图Fig.6 u（t）－s（t）phase track atα＝1.8

图7 α＝5.5时u（t）－s（t）相位图Fig.7 u（t）－s（t）phase track atα＝5.5

3 结论

本文设计了具有反馈的单神经元模型的非线性动力学行为的电路，推导了电路的参数.对实现非单调激活函数的单元电路方法及电路参数设计分析较为详细，并进一步利用仿真软件进行了仿真实验研究.结果表明，运用EWB 所设计电路的正确性.由于EWB软件仪器的控制面板外形和操作方式都与实物相似，可以实时显示测量结果.且它采用的是实际电路元件模型，所以其仿真实验结果与示波器从实际硬件电路得到的结果相近，因而该混沌系统的仿真实验结果是有效的.本文所做的工作对深入分析和促进混沌技术应用具有重要的意义.有关此类动力学系统的电路实现设计及在工程技术中的实际应用作者将作进一步的研究.

［1］Yassen M T.Adaptive control and synchronization of a modified Chuas'circuit system ［J］.Applied Mathematics and Computation，2003，113（1）：113－128.

［2］Chua L O，Komuro M，Matsumoto T.The double scroll family［J］.IEEE Trans Circ Sys I，1986，3（11）：1072－1118.

［3］毛北行，王东晓，卜春霞.Lurie混沌系统的脉冲控制同步［J］.华 中 师 范 大 学 学 报：自 然 科 学 版，2012，46（3）：297－299.

［4］Li C G，Chen G R.Coexisting chaotic attractors in a single neuron model with adapting feedback synapse［J］.Chaos，Solitons Fractals 2005，23：1599－1604.

［5］Zou F，Nossek J A.Bifurcation and chaos in cellular neural network［J］.IEEE Trans Circ Sys I，1993，40（3）：166－172.

［6］Li C G，Yu J B，Liao X F.Chaos in a three－neuron hysteresis Hopfield－type neural network［J］.Phys Lett A，2001，285：368－372.

［7］Li C G，Chen G R，Liao X F.Hopf bifurcation and chaos in tabu learning neuron models［J］.Int J Bifur Chaos，2005，15：2633－2642.

［8］Bondarenko V E.High－dimensional chaotic neural network under external sinusoidal force［J］.Phys Lett A，1997，236：513－519.

［9］Li C G，Chen G R，Liao X F，et al.Hopf bifurcation and chaos in a single inertial neuron model with time delay［J］.Eur Phys J B，2004，1：337－343.

［10］马 军，苏文涛，高加振.Hindmarsh－Rose混沌神经元自适应同步和参数识别的优化研究［J］.物理学报，2010，59（3）：1554－1561.

［11］陈 军，李春光.具有自适应反馈突触的神经元模型中的混沌：电路设计［J］.物理学报，2011，60（5）：5031－5037.

［12］周小勇.一个新混沌系统及其电路仿真［J］.物理学报，2012，61（3）：71－79.

［13］王冠华.Multisim10电路设计及应用［M］.北京：国防工业出版社，2008.

［14］李险峰，褚衍东，徐冬亮，等.一个新类Lorenz混沌系统的动力学分析及电路仿真［J］.四川大学学报：自然科学版，2008，45（5）：1167－1173.

［15］陈 军，李春光.禁忌学习神经元模型的电路设计及其动力学研究［J］.物理学报，2011，60（2）：5021－5029.

［16］Neamen D A.Electronic Circuit Analysis and design（2nd ed）［M］.Boston：McGraw－Hill，2001.