基于MATLAB实现同步电机自同步并列的仿真

许 强，陈巧玲，侯永辉，钱俊良，宋 喆

(华北水利水电学院，河南郑州450045)

同步电机的异步并列是指定值励磁电压、定值转速(但不同于同步转速)的电机突然与电力系统并列.这是一种严重的误操作，对电机本身以及整个系统的运行都可能造成严重破坏［1］.同步电机的自同步并列是指电机由原动机驱动至接近同步转速时投入电力系统，并在投入系统的同时或稍后，投入其直流励磁，使其在与逐渐增大的励磁电流相对应的交变转矩作用下进入同步［1］.与异步并列相比，自同步并列的电流和转矩都最小，故后者被认为属正常操作.自同步并列虽然合闸及投入励磁时会对电网及发电机本身产生强大的冲击电流，但它最突出的优点是毋需选择并列合闸时机，操作非常简单，因而在我国南方诸多的小型水电站中有着较多的应用，所以对工程实际也具有一定的意义［2］.

MATLAB是主要面对科学计算、可视化以及交互式程序设计的高科技计算环境.笔者用MATLAB进行编程，采用变步长积分法，对刚性、非线性、非连续性系统进行精确仿真，并借助其曲线图形，可以方便地实现仿真的可视化.

1 自同步的物理过程

自同步时，转子转速异于同步转速.自同步过程中，投入励磁前，同步电机的定子绕组中共有5组电流分量，即直流分量、以同步角频率和以2(1－s)，(1－s)，(1－2s)角频率交变的交流分量;励磁绕组中共有3个电流分量，即直流分量和以s，(1－s)角频率交变的交流分量;投入励磁后，在外施的直流励磁电压作用下，励磁绕组中又将逐渐出现一个直流电流分量;相应地，定子绕组中也将出现1组以(1－s)角频率交变的交流电流分量.因此，自同步暂态过程中的电磁转矩包含7类分量，即单向分量、以角频率 s，2s，1，(1 －s)，(1 －2s)，2(1 －s)交变的交变分量.在这些转矩分量中，投入励磁后以角频率s交变的分量，对电机能否进入同步关系最密切.它们的作用就在于使机组的瞬时转差产生周期脉动;而且，随时间的增加，转差脉动的幅值也逐渐增大，以致在某一瞬间，瞬时转差可能抵达零值并开始改变符号，机组开始进入同步.

2 同步电机的状态空间方程

运用计算机计算同步电机自同步的暂态过程时，可直接引用以派克分量表示的状态空间表达式(1).由于自同步并列属对称三相运行方式，可删去其中零轴分量之间的关系式.式中的电压列向量udq0的初值和电流列向量idq0的初值因研究的具体运行方式而异.在dq0坐标系统中以电流的派克分量为状态变量时的状态空间方程［1］(用标幺值表示)为

式(1)可以简写为

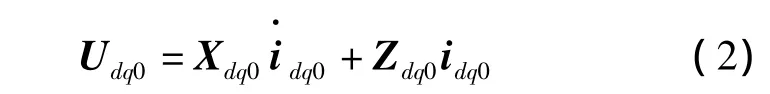
由式(2)可得

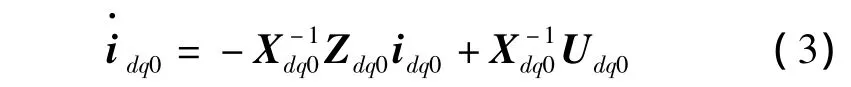
式中:ud，uq，uf为各绕组电压的瞬时值;id，iq，if，iD，iQ为各绕组电流的瞬时值;xd为直轴同步电抗;xq为交轴同步电抗;xf为励磁绕组电抗;xD为直轴阻尼绕组电抗;xQ为交轴阻尼绕组电抗;xaf，xfD，xaD分别为定子绕组、励磁绕组、直轴阻尼绕组3个绕组相互之间的互感电抗且xaf=xfD=xaD=xad(xad为直轴电枢反应电抗);xaQ为定子绕组和交轴阻尼绕组之间的互感电抗;r为定子电阻;w为转子的电角速度，此时w=(1－s).

2.1 仿真算法的实现

根据图1中所示同步电机稳态运行时各个量之间的关系［3］，求出同步电机自同步并列前的电机端电压 ud［0］和 uq［0］，投入的励磁电压 uf分别为:

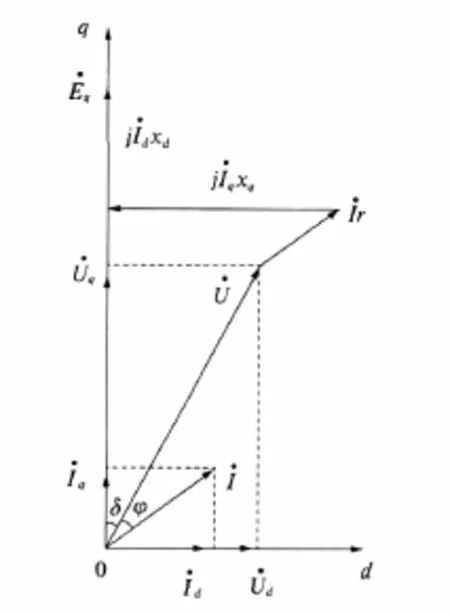
图1 同步电机电势向量图

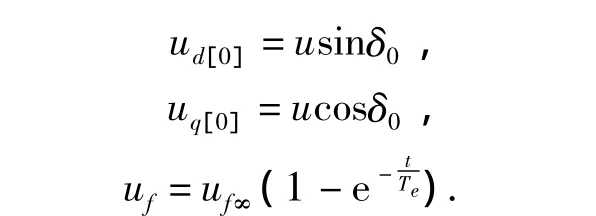
显而易见，式(1)的解是一个常系数常微分方程的初值问题，故可以用变步长龙格—库塔法等计算.此方法可以用MATLAB中的ode45命令，它采用四阶、五阶 runge-kutta单步算法，截断误差为(Δx)3.此命令解决的是Nonstiff(非刚性)的常微分方程，是解决数值解问题的首选方法.下面给出自同步投入电机的同时投入其励磁运行方式下的初值:

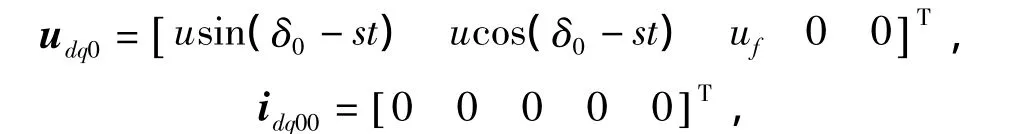
式中:udq0为电压列向量;idq00为电流列向量的初值;s为转差率;δ0为并列瞬间的功率角.

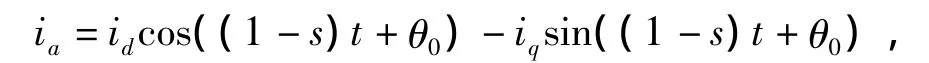
式中:s为转差率;θ0为转子位置角，代入式(4)中，

可得自同步并列时的电磁转矩.

根据上述原理，可以画出同步电机自同步并列计算流程，如图2所示.

图2 同步电机自同步并列仿真流程

2.2 仿真实例

在同步电机自同步并列的仿真中，以1台典型的同步电机为例来说明仿真的过程.其同步电机的电机参数(标幺值)如下.

若给出自同步投入励磁前的运行方式下的初值:

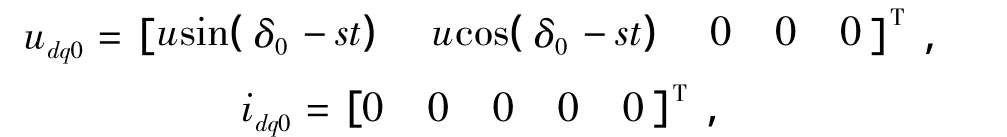
还以上述典型的同步电机为例，按类似的方法可以仿真出自同步投入励磁前的电磁转矩，如图8所示.

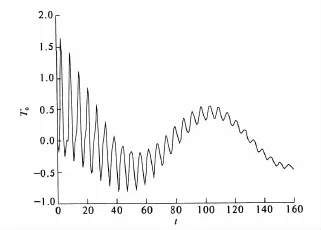
图8 自同步并列投入励磁前的电磁转矩T0的波形

若不计定子绕组电阻，因为投入励磁而出现的等值定子绕组合成磁链增量为零，所以，投入励磁后的电磁转矩，只比投入励磁前的电磁转矩多两个分量，如图9所示.

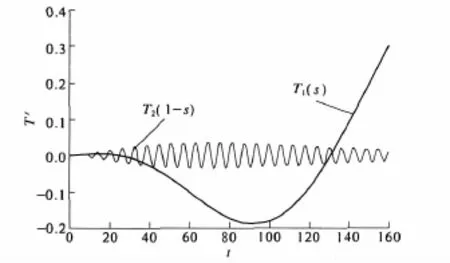
图9 自同步投入励磁后增加的电磁转矩分量T'的波形

2.3 实例仿真结果分析

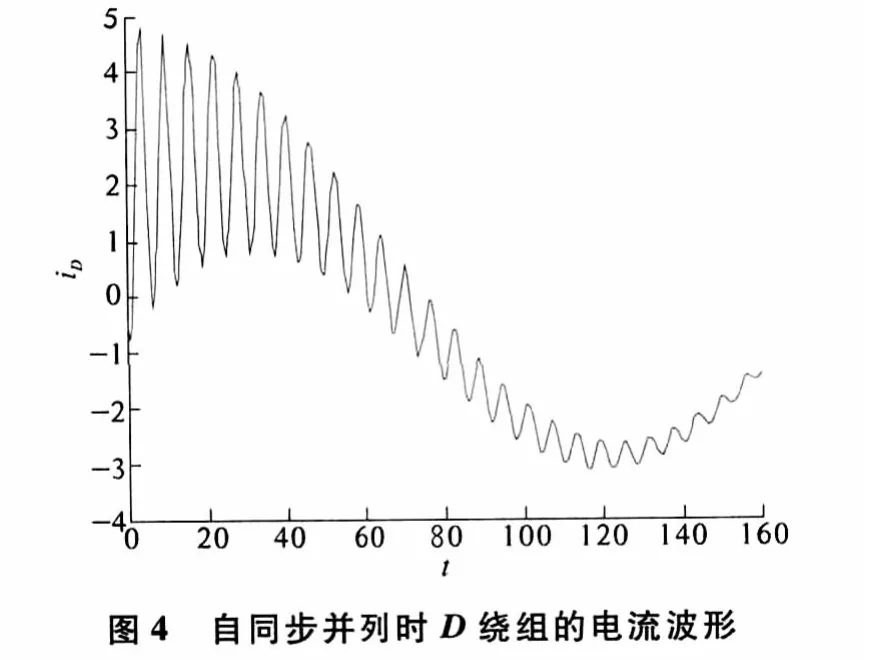
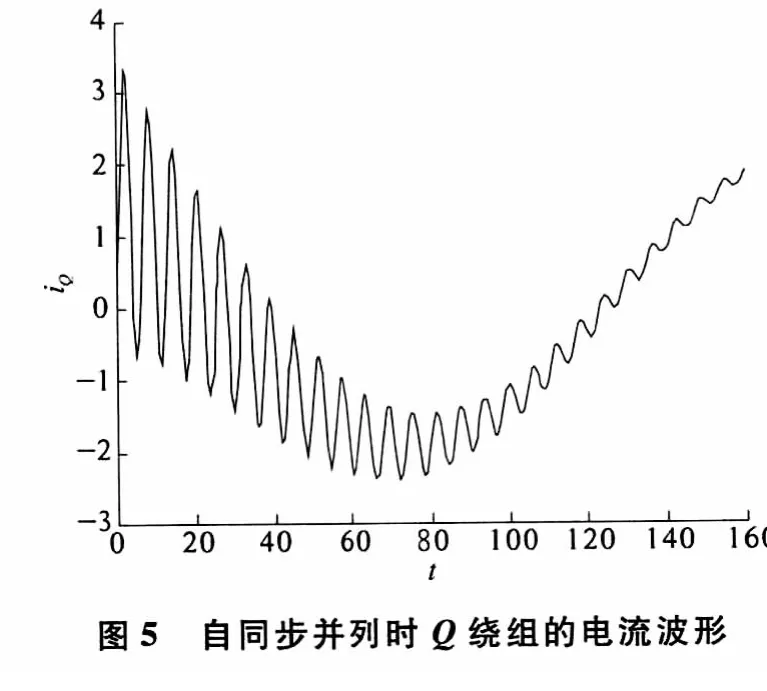
由图3—7可以看出，当进行自同步并列时，各绕组电流和转矩都很小.各绕组电流刚开始会发生强烈震荡，特别是定子上面的相电流最为突出，由于定转子电流产生的磁场相互作用，刚开始会产生比较大的电磁转矩，随着电流的衰减，磁场的减弱，转矩也周期性地逐渐衰减，最终被拖入同步.

由图7—9可知，图7是图8与图9的叠加，而由图9可见，在投入励磁的初始阶段，这些转矩分量都相对较小.经比较可知，即使在投入电机的同时投入其励磁，也不会给电机带来更大的冲击.因此，在电力系统发生事故、频率波动较大的情况下，用自同步并列可以迅速把备用机组投入电网运行，作为处理系统事故的重要措施之一.

3 结语

利用MATLAB工具对同步电机自同步并列做了仿真分析，编程简单，并可直接对输出结果进行分析.计算机算法具有简单、精确、灵活等独特优点，但具有物理概念不清晰等缺点.若计及电机各绕组的电阻，分析这类暂态过程的初始阶段，运用解析法简化计算公式计算，仍不失为一种可取的办法，将是下一步需要解决的问题.

［1］陈珩.同步电机运行基本理论与计算机算法［M］.北京:水利电力出版社，1992.

［2］张志强.能量变换器自同步并列和非同期并列的研究［D］.哈尔滨:哈尔滨理工大学，2008.

［3］李光琦.电力系统暂态分析［M］.北京:中国电力出版社，2007.

［4］吴天明，谢小竹，彭彬.MATLAB电力系统设计与分析［M］.北京:国防工业出版社，2007.

［5］彭建飞，任眠，王树锦.MATLAB在电力系统仿真研究中的应用［J］.计算机仿真，2005，22(6):193 －196.

［6］ Mahseredjian J，Alvarado F.Creating an electromagnetic transients program in MATLAB:Motets［J］.IEEE Trans on Power Delivery，1997(12):380 －388.