福建省5种造林树种幼苗生物量估测模型
马玉珠,程栋梁,钟全林,徐朝斌,靳冰洁
(福建师范大学 地理科学学院/湿润亚热带山地生态国家重点实验室培育基地,福建 福州 350007)
生物量作为植物群落能量基础和营养物质的重要组成部分,是生态系统生产力的重要体现[1]。准确测定森林生物量是深入研究林业和生态问题的基础,特别是在评价森林生态系统碳循环过程中具有不可替代的作用[2]。
福建省地处亚热带,气候温和,雨量充沛,光照充足,土壤肥沃,十分适合林木生长,森林覆盖率达63.1%,居全国第一[3]。全省有高等植物4 703种,占全国高等植物种类的15.7%,其中,裸子植物以中国特有的马尾松(Pinus massoniana)为主,杉木(Cunninghamia lanceolata)广布全省,是构成常绿针叶林的主要成分[3]。刨花楠(Machilus pauhoi)、闽楠(Phoebe bournei)和木荷(Schima superba)是福建省主要的常绿阔叶造林树种。
目前对马尾松、杉木的成株生物量估测研究比较普遍[4-5],但对刨花楠、闽楠、木荷3种常绿阔叶树种的研究较少,本文以福建省内5种常见乔木树种为研究对象,构建其幼苗生物量估测模型,这对准确评价苗木及其构件生物量,分析苗木构件生物量分配对其生长的影响及快速判别苗木优劣等方面具有重要理论意义和实际应用价值。
1 材料与方法
1.1 研究地概况
本研究实验区位于顺昌县林业科技推广中心苗圃。顺昌县为福建省南平市下辖县,地处福建西北,武夷山脉南麓,位于北纬 26°38'~27°121',东经 117°29'~118°14'。境内以山地、丘陵地貌为主,属中亚热带海洋性季风气候,年平均气温19℃,年平均降雨量2 051 mm。气候土壤资源得天独厚,全县拥有国家级、省级生态保护林约3万hm2,森林覆盖率82.8%,绿化程度95.1%,超发达国家水平,素有“林海粮仓果乡”之美誉。该区是马尾松、杉木、刨花楠、闽楠和木荷的典型分布区。
1.2 测定项目与方法
研究样木为马尾松、杉木、刨花楠、闽楠和木荷1~2年生幼苗。于2012年12月和2013年4月对实验地幼苗生长情况进行调查。分别树种随机选取生长状况良好的苗木,每种50株以上(表1,闽楠因苗木数量不足,仅测量19株)。对各样苗分别测量其株高(H)、基径(D)和冠幅宽度(C)。株高用钢卷尺测量,基径用游标卡尺测量;冠幅分南北和东西方向测量,取平均值。将苗木根部去土洗净后,分别根、茎、叶,将其放在75℃烘箱烘干至恒质量后,测定其生物量(表1)。
冠层面积(canopy area,CA)和冠层投影体积(canopy projected volume,CV)采用如下公式计算[6]:
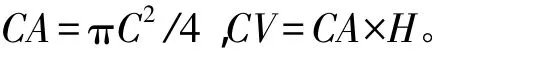
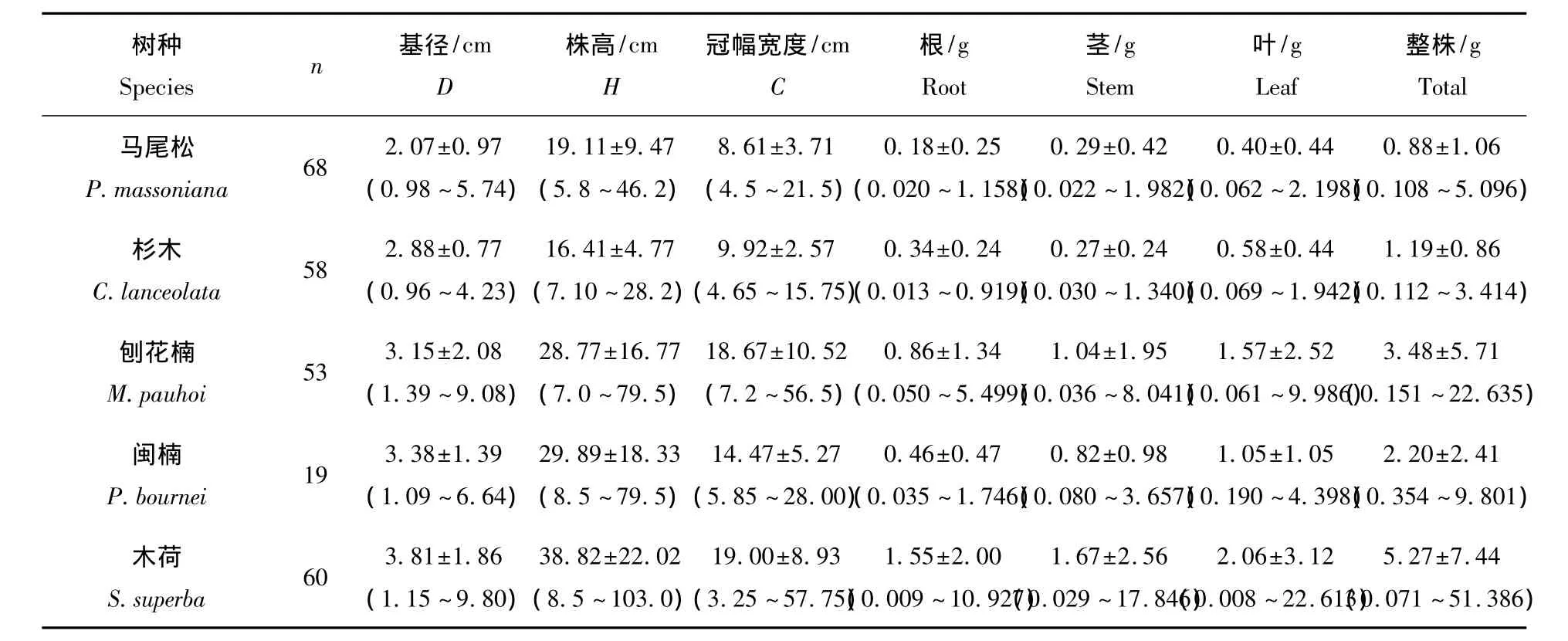
表1 5种苗木生物量估测模型因变量和部分自变量概况Tab.1 Dependent variables and partial independent variables summary of biomass estimation model for five types of saplings
1.3 数据处理
选取基径(D)、株高(H)、冠幅宽度(C)及复合变量D2、D2H、CA和CV作为自变量,幼苗根、茎、叶及整株生物量作为因变量,选用5种回归方程(线性方程y=a+bx、二次多项式y=a+bx+cx2、指数方程y=aebx、幂函数y=axb和对数方程y=a+blnx)构建生物量估测模型,其中y为各器官或整株生物量,x为选取自变量中的任一变量,a、b、c为待估参数。
采用SPSS17.0软件进行统计和回归分析,并根据决定系数R2和SEE(standard error of the estimate)对所构建生物量模型进行拟合优度的评估和比较。
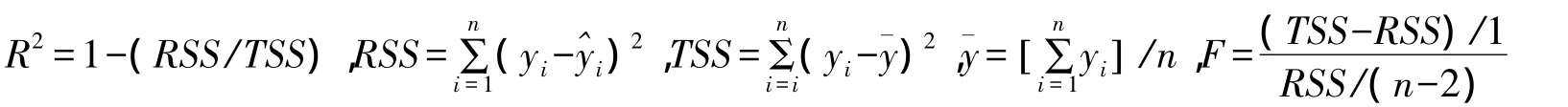
2 结果与分析
研究共拟合幼苗生物量回归方程700(5×7×4×5)个。综合来看,R2以幂函数、二次多项式最高,其次为一次线性式,指数方程和对数方程最低。700个回归方程在此不一一赘述,5种乔木幼苗各器官及整株生物量最优模型整理后列于表2。
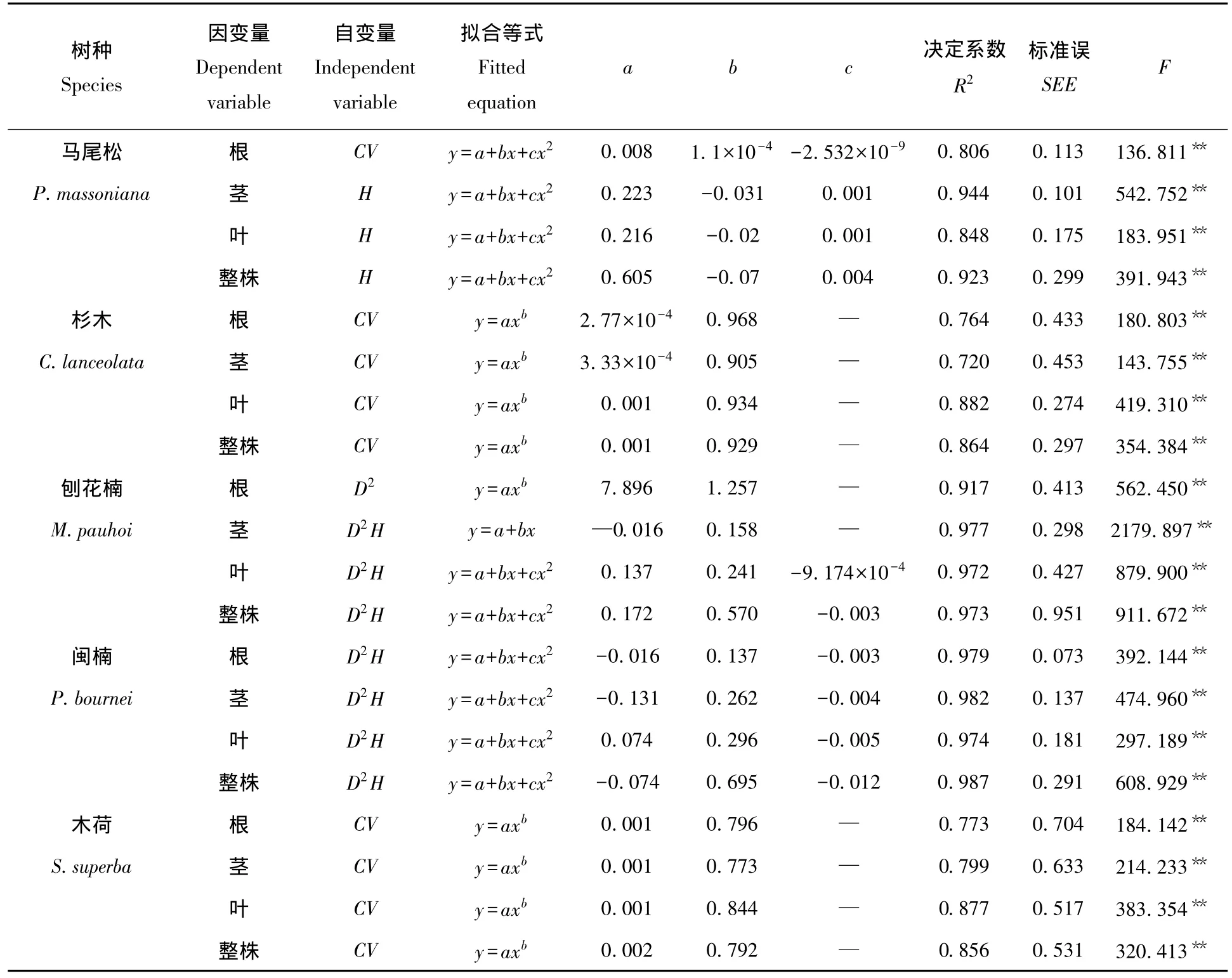
表2 5种幼苗生物量最优拟合方程Tab.2 Best biomass fitted equations for five types of saplings
5种苗木各器官及整株生物量的最优模型均统计显著(P<0.001)(图1-5),决定系数R2的变化范围从杉木茎器官的0.720到闽楠整株生物量的0.987。
马尾松和闽楠各器官及整株生物量的最优拟合形式均为二次多项式,但其自变量不同:闽楠整株及各器官最优模型的自变量为D2H;马尾松根器官最优模型的自变量为CV,茎、叶和整株生物量最优模型的自变量为H。杉木和木荷各器官及整株生物量的最优拟合模型为幂函数,自变量均为CV。刨花楠根器官的最优拟合形式为幂函数,其自变量为D2;叶和整株生物量最优拟合模型为二次多项式,茎器官生物量最优拟合模型为一次线性式,但其自变量均为D2H。
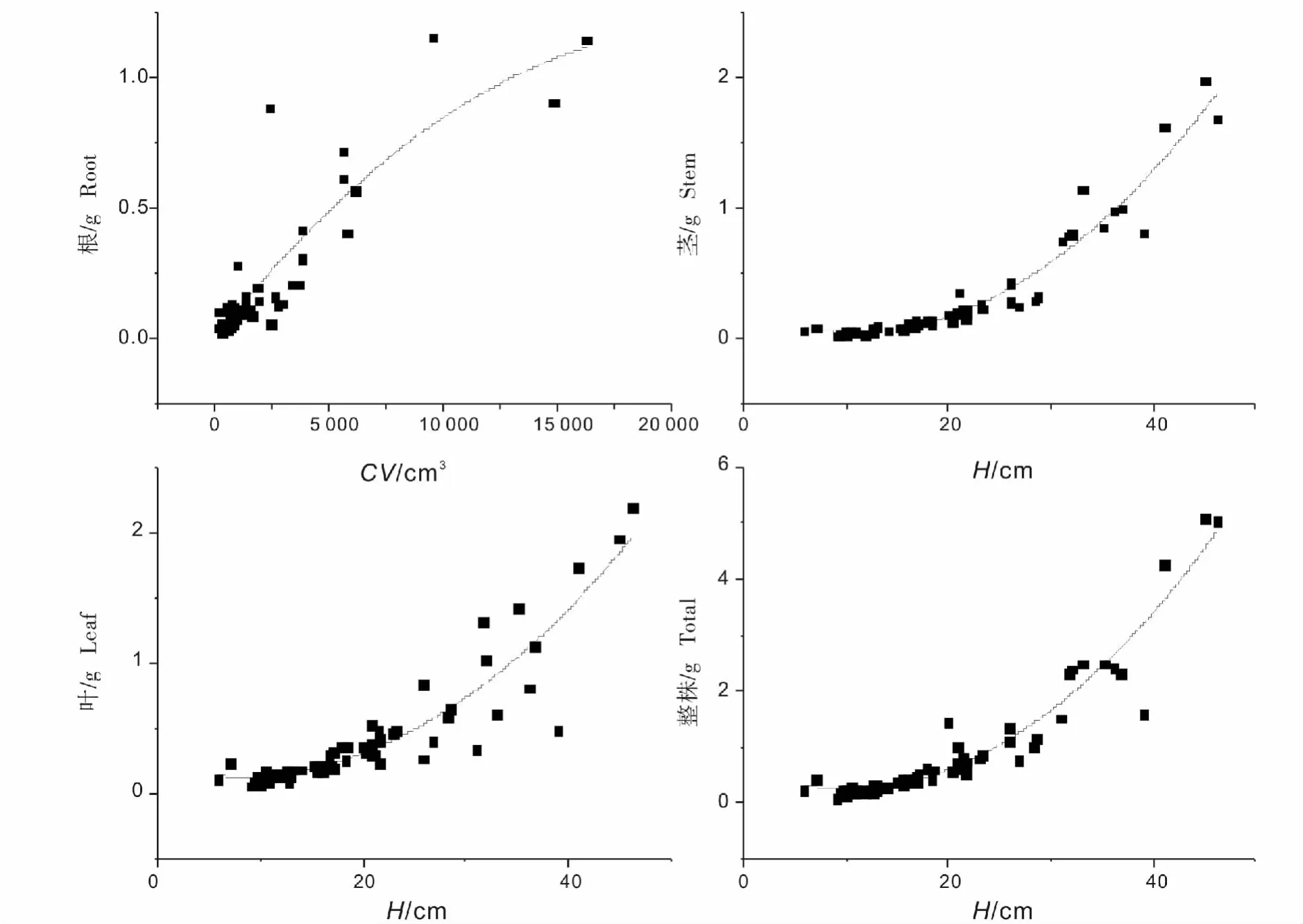
图1 马尾松最优拟合模型Fig.1 Best fitted models for Pinus massoniana
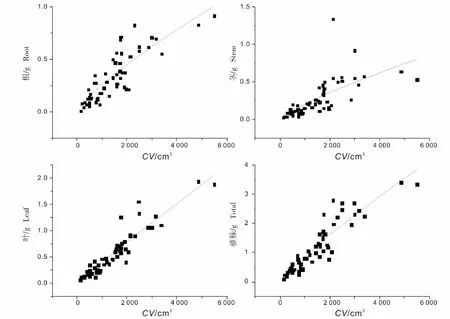
图2 杉木最优拟合模型Fig.2 Best fitted models for Cunninghamia lanceolata
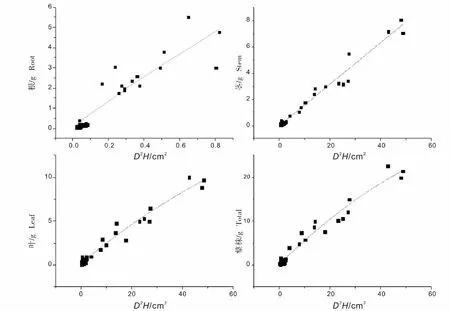
图3 刨花楠最优拟合模型Fig.3 Best fitted models for Machilus pauhoi
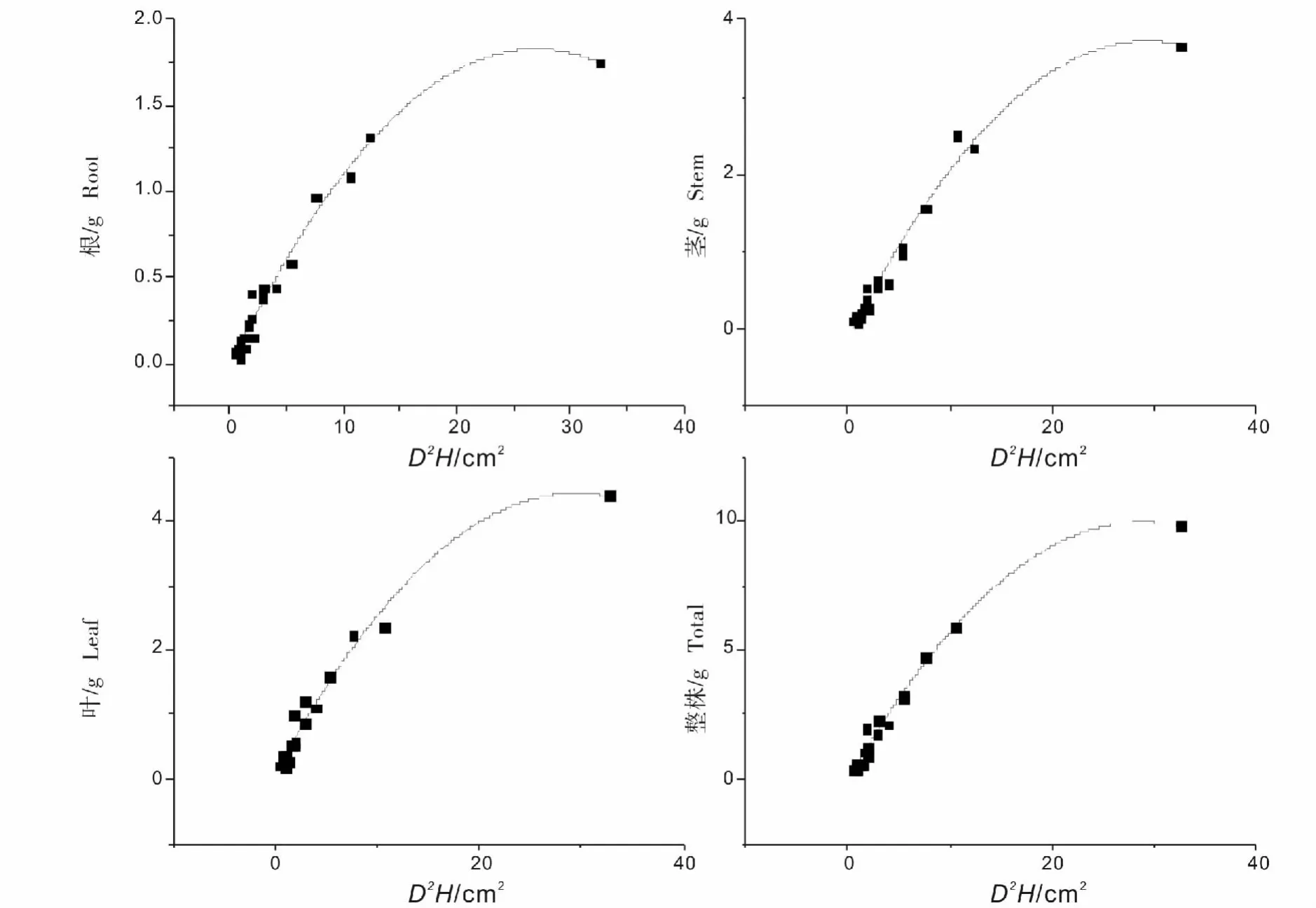
图4 闽楠最优拟合模型Fig.4 Best fitted models for Phoebe bournei
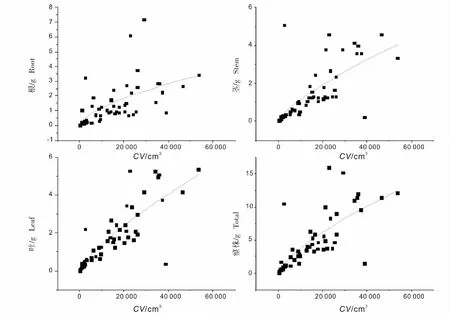
图5 木荷最优拟合模型Fig.5 Best fitted models for Schima superba
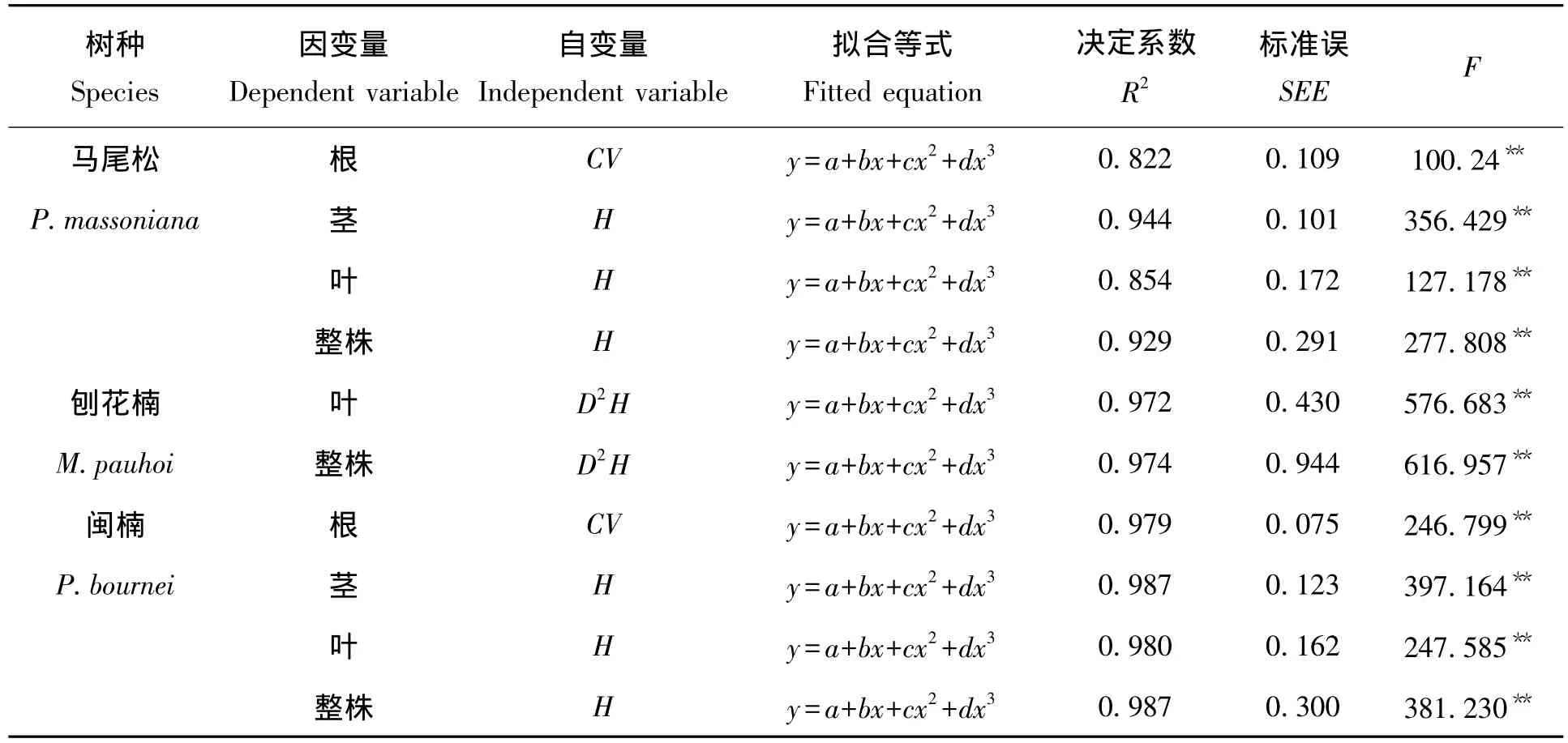
表3 3次多项式拟合结果Tab.3 The fitted results of cubic polynomial
3 讨论
本文选取D、D2、H、D2H、C、CA和CV作为自变量建立回归模型。在一些研究中,D被认为是最好的自变量指标[7-10]。由于本研究实验材料为幼苗,因此用基径(D)代替胸径(DBH)。针对闽楠、刨花楠,当D和H组成复合变量D2H时,拟合效果显著增强。通常认为以(DBH)2H作为自变量的幂函数模型是最好的估测模型[2,4-5,11-12],但本研究中,凡是以 D2H 作为自变量的模型,均是以二次多项式的形式出现;以幂函数形式出现的最优模型,自变量均为CV。说明幼苗生物量最优估测模型不同于成熟个体。有研究表明CV也可以作为植物生物量估测的适宜变量[6,13],本研究中,CV与杉木、木荷各器官及整株生物量之间具有很好的回归关系。
异速生长方程通常被用来进行生物量估测[14-17],其本身就是幂函数形式,本研究中杉木和木荷的最优拟合模型均为幂函数,幂函数占本研究最优模型总数近1/2(9/20),可见用幂函数评估苗木生物量是较好的。
马尾松和闽楠两种乔木幼苗的最优拟合模型均为二次多项式,5种乔木幼苗的20个最优拟合模型中,二次多项式为10个,占总数量的1/2。对于同一组自变量和因变量,通常三次多项式比二次多项式拟合效果好,二次多项式比一次线性式拟合效果好,这表明次数越高,拟合效果越好。然而当拟合多项式的次数较高时,其正规方程组往往是病态的,因此要尽量少做高次拟合,故本研究生物量估测模型中多项式拟合只做二次拟合。
本文建立的5种乔木幼苗各器官及整株生物量估测模型大多达到了较高的拟合度,但在应用时要谨慎。由于样木的采集获取集中于顺昌县林业科技推广中心苗圃,光照、土壤以及区域环境等因素对幼苗生物量及其分配影响较大,因此,在研究区外应用本结果还有待进一步验证;同时对于D和H超出本研究测定范围的幼苗,在应用本研究模型时,预测结果也可能出现较大误差。
[1]冯宗伟,王效科,吴刚.中国森林生态系统的生物量和生产力[M].北京:科学出版社,1999:6-65.
[2]范春楠,庞圣江,郑金萍,等.长白山林区14种幼树生物量估测模型[J].北京林业大学学报,2013,35(2):1-9.
[3]福建省林业厅.福建林业概况[EB/OL].[2013-7-5].http://www.fjforestry.gov.cn.
[4]蔡梅生.中国杉木林地地上地下生物量分配研究[J].林业勘察设计,2009(1):95-98.
[5]张国斌,李秀芹,佘新松,等.安徽岭南优势树种(组)生物量特征[J].林业科学,2012,48(5):136-140.
[6]Zeng H Q,Liu Q J,Feng Z W,et al.Biomass equations for four shrub species in subtropical China[J].J For Res,2010,15:83-90.
[7]Clough B F,Scott K.Allometric relationships for estimating above-ground biomass in six mangrove species[J].For Ecol Manag,1989,27:117-127.
[8]Haase R,Haase P.Above-ground biomass estimates for invasive trees and shrubs in the pantanal of mato grosso,brazil[J].For Ecol Manag,1995,73:29-35.
[9]Paton D,Azocar P,Tovar J.Growth and productivity in forage biomass in relation to the age assessed by dendrochronology in the evergreen shrub Cistus ladanifer(L.)using different regression models[J].J Arid Environ,1998,38:221-235.
[10]Paton D,Nunez J,Bao D,et al.Forage biomass of 22 shrub species from Monfrague Natural Park(SW Spain)assessed by log-log regression models[J].J Arid Environ,2002,52:223-231.
[11]罗天祥.中国主要森林类型生物生产力格局及其数学模型[D].北京:中国科学院国家计划委员会自然资源综合考察委员会,1996.
[12]范文义,张海玉,于颖,等.三种森林生物量估测模型的分析比较[J].植物生态学报,2011,35(4):402-410.
[13]徐朝斌,钟全林,程栋梁,等.基于C2H和D2H的刨花楠幼苗生物量回归模型比较研究[J].华南农业大学学报,2013,34(4):543-547.
[14]李春萍,李刚,肖春旺.异速生长关系在陆地生态系统生物量估测中的应用[J].世界科技研究与发展,2007,29(2):51-57.
[15]Shaiek O,Loustau D,Trichet P,et al.Generalized biomass equations for the main aboveground biomass components of maritime pine across contrasting environments[J].Annals of Forest Science,2011,68(3):443-452.
[16]Armeecin R B,Coseco W C.Abaca(Musa textilis Nee)allometry for above-ground biomass and fiber production[J].Biomass and Bioenergy,2012,46:181-189.
[17]Subedi M R,Sharma R P.Allometric biomass models for bark of Cinnamomum tamala in mid-hill of Nepal[J].Biomass and Bioenergy,2012,47:44-49.

