“巧妙点”的再探究

●何君青 (南京师范大学附属中学新城初中 江苏南京 210019)

“数学是思维的体操”，可以锻炼学生的思维能力，使其不断地发展.作为一名教师，应当在教学过程中创设一系列有价值的问题，这一系列问题往往表现为一个系统，蕴含着丰富的思想和方法.笔者最近在一篇文章中创设了一系列问题，在稿件修改的过程中经过多次斟酌和修改收获颇丰，为把文章的部分环节再深入研究，经思考后，本文就其中一个问题展开深入探索，愿与读者分享.

原题呈现 平面上，若点P与点A，B构成的△PAB是等腰三角形，我们称点P是点A，B的“巧妙点”.类似地，平面上，若点P与点A，B，C中的任意2个点构成的△PAB，△PBC，△PCA均是等腰三角形，我们称点P是点A，B，C的“巧妙点”，或称点P是△ABC的“巧妙点”.探索：若点 A，B，C存在“巧妙点”，则如何作出这3个点的“巧妙点”?

分析由于点A，B，C的位置并未确定，需要考虑三点共线和不共线的情形，况且原文以探究课的形式呈现，并未深入研究个别角需要具备的条件，故笔者在三点共线的情形下解答如下：

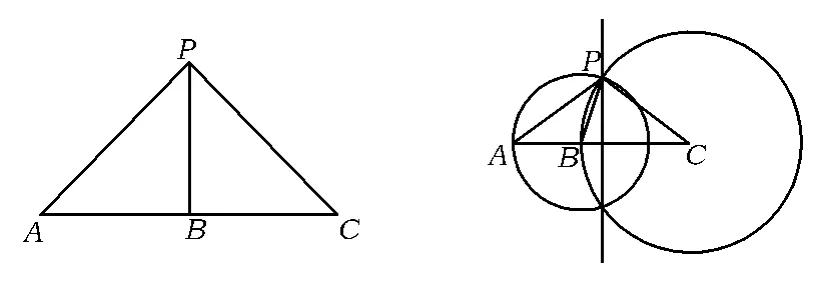
图1 图2

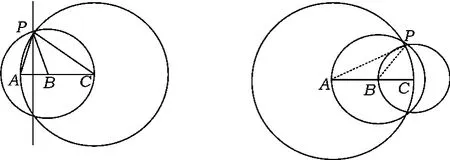
图3 图4

若点A，B，C共线，则不能构成三角形，如图1～4可以分以下4种情况(由于点的任意性，相同方法下仅以一种情况为例)：

(1)如图1，考虑特殊情况：当B为AC的中点时，点P即为“巧妙点”;

(2)如图2～4，当点B不为AC中点时，可以利用垂直平分线、两圆的交点或三圆交点找到“巧妙点”，此时∠A，∠C，∠APB有特定的度数(课后思考).

思考 根据图1～4的描述，已经作出了三点共线情形下的“巧妙点”.由于课堂时间的限制，笔者在课堂上并未让学生具体算出∠A，∠C，∠APB，仅是利用几何画板的演示让学生清晰地感受到三点共线情况下“巧妙点”如何作出.但课后学习能力较好的学生进行了探索，笔者也进行了计算，发现4种情形下的∠A，∠C，∠APB的大小是可以求得的，而且通过3个角的确定也能将点P的位置确定下来，可见求得∠A，∠C，∠APB是有价值的.

解(1)当B为AC中点时，如图1，只要点P能使△PAB，△PBC，△PCA均为等腰直角三角形即可，很容易求出∠A=45°，∠C=45°，∠APB=45°.

(2)当B不为AC中点时，

①如图2，以点B为圆心、BA为半径作圆⊙B，以点C为圆心、CB为半径作圆⊙C，再作线段AC的垂直平分线，两圆公共点且在垂直平分线上的这个点即为“巧妙点”P.因为在⊙B，⊙C中，BA=BP，CB=CP，所以

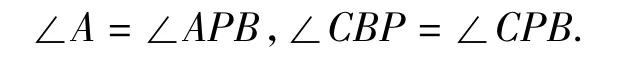
在△PCA中，由 PA=PC，得

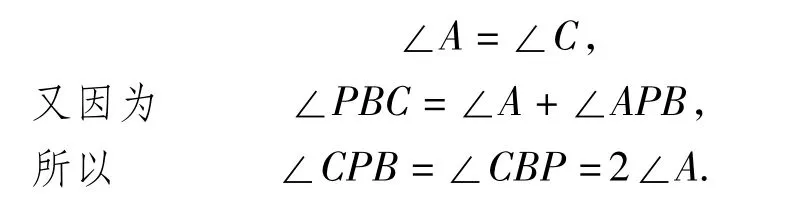
由∠A+∠C+∠APC=180°，得

②如图3，以点B为圆心、BC为半径作圆⊙B，以点C为圆心、CA为半径作圆⊙C，再作线段AB的垂直平分线，两圆公共点且在垂直平分线上的这个点即为“巧妙点”P.因为在⊙B，⊙C中，CB=BP，CA=CP，所以

③如图4，以点A为圆心、AC为半径作圆⊙A，以点B为圆心、BA为半径作圆⊙B，以点C为圆心、CB为半径作圆⊙C，三圆公共点即为“巧妙点”P.因为在⊙A，⊙B，⊙C 中，AP=AC，BA=BP，CB=CP，所以

通过上面的解答可知，若点A，B，C存在“巧妙点”，则作出巧妙点，还可以确定共线的3个点满足什么条件时存在“巧妙点”.一道题的深入研究让题目更趋于完美.

本题还可以进一步推广：对共线的4个点进行“巧妙点”的探索.如图5，共线的4个点A，B，C，D 的“巧妙点”情形：以点 A为圆心、AC为半径作圆⊙A，以点B为圆心、BA为半径作圆⊙B，以点D为圆心、DB为半径作圆⊙D，三圆公共点即为“巧妙点”P.利用前面的方法可以求出此时∠A= ∠D=36°，∠APB= ∠DPC=36°，∠ABP=∠DCP=108°.

学习数学就应在一定程度上理解其本质，掌握其方法及规律，继而会一题，解一类.不能走“题海战术”、“强化训练”的老路，要开展探究规律性学习，让学生认识数学的特点，归纳出每一类题的特征，这样才能提高学生的答题能力，真正解题时才可得心应手.

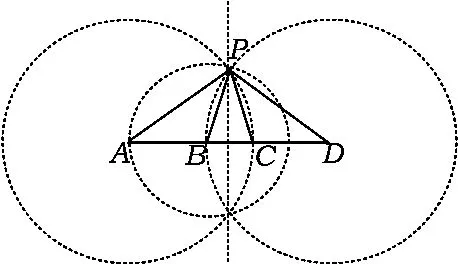
图5