基于多目标遗传算法的磁轴承结构优化设计

张松山，周 瑾，张发品

（1.南京航空航天大学机电学院，江苏 南京 210016；2.94795部队，安徽 芜湖 241007）

0 引言

磁悬浮轴承简称磁轴承，是利用磁场力将转轴无机械摩擦、无润滑地悬浮于空间，并且轴心位置可由控制系统控制的一种新型轴承。应用于航空压缩机、计算机硬盘、军事制导及高速机床等多个方面。其中，磁轴承的承载力历来是工程设计中所关注的主要指标，而磁轴承所能提供的最大载荷最终要受到铁芯磁饱和的限制。利用多目标遗传算法MOGA（multiple objective genetic algorithm）［1］，基于ANSYS Workbench多物理协同仿真平台，在转子外径、工作气隙和工作电流一定的情况下，通过调整和优化磁轴承磁路上部件的结构参数，以达到最大地发挥铁芯的磁通量，提升磁轴承承载力的目的。

1 优化算法

MOGA多目标遗传算法引入了Pareto秩的概念来进行适值分配，保持了种群多样性和提高了算法的搜索效率等［1］。其基本的优化流程如图1所示。在多峰值优化问题中会因为早熟而存在“遗传漂变”问题，MOGA因为引入了适值分享的概念［2］和交配限制的方法［3］，很好地解决了这个问题。该方法能够快速自动地找到最优参数，避免了烦琐的试验过程，提高了优化效率［4］，MOGA集成在ANSYS优化模块中，其优化技术已经较为成熟，能基本解决工程上的一些优化问题。

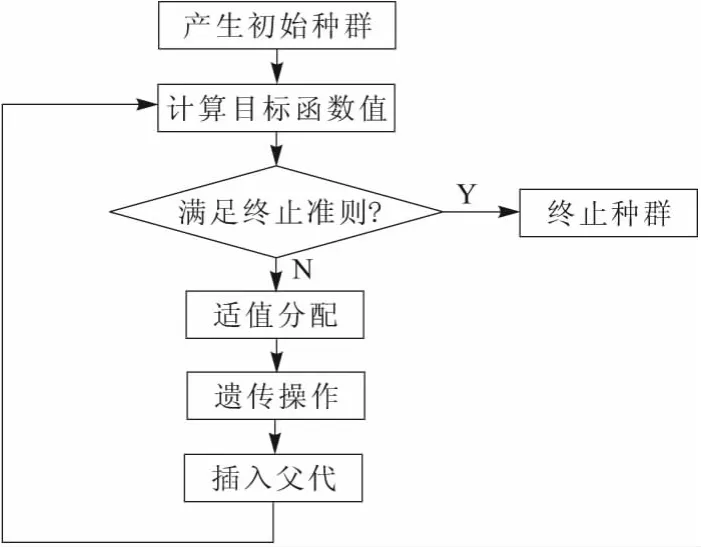
图1 多目标遗传算法基本流程

2 磁轴承参数化建模

所要优化的磁轴承是集轴向单自由度磁轴承、径向二自由度磁轴承于一体的径向-轴向三自由度磁轴承，可同时实现径向2个自由度和轴向单自由度的联合控制［5-7］。为便于优化设计，对模型的关键尺寸进行参数化设计。径向磁轴承和轴向磁轴承采用CATIA V5R20三维建模软件建模，完成后导入ANSYS Workbench的Design Modeler建模模块。为保证径向磁轴承的一个完整磁路，在不影响计算精度情况下尽量减少单元提高分析效率而采用了1／4分析模型，最后建好的1／4模型如图2所示。径向磁悬浮轴承和轴向磁悬浮轴承一起安装在转子的一端，两者的磁场会相互地影响，即磁路会有一定耦合，利用理论公式来计算磁悬浮轴承的承载力误差会较大，而利用有限元会较好地解决这个问题。

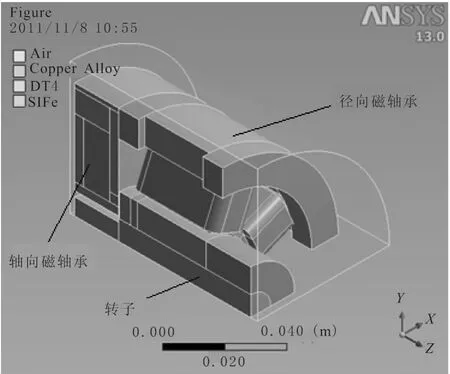
图2 磁悬浮轴承的1／4模型

3 优化目标和优化参数

3.1 优化对象

优化目标：在转子外径、气隙和工作电流不变的情况下，径向磁悬浮轴承单个磁极的电磁力最大、轴向磁悬浮轴承的电磁力最大。

优化参数如图3所示，提取结构的参数如表1所示。

3.2 磁场分析

磁场分析的边界条件为：

a.径向磁悬浮轴承线圈加载大小为1A的电流。

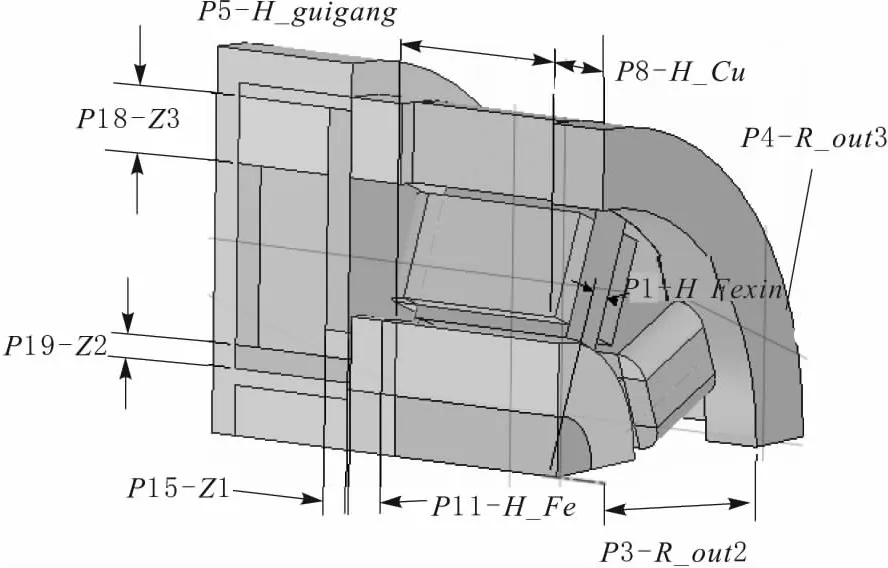
图3 磁悬浮轴承磁路关键结构参数

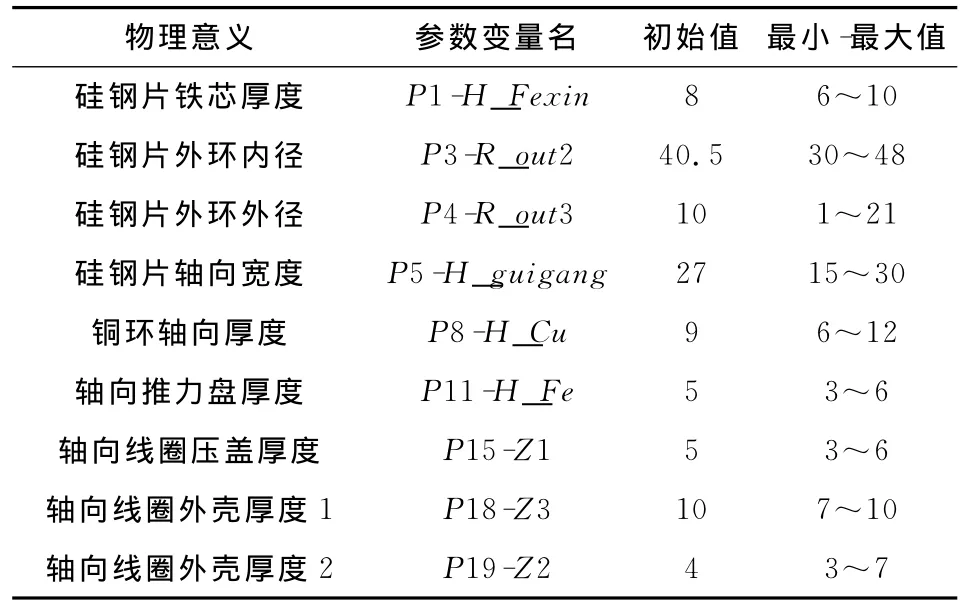
表1 磁轴承关键结构参数表 mm

b.轴向磁悬浮轴承线圈加载大小为1A的电流。

c.模型的表面（对称处表面除外）磁通量为零。

边界条件如图4所示。优化目标参数提取，经过计算，提取了转子组件所受3个方向的磁拉力，具体如表2所示。

表2 磁场仿真磁拉力结果表 N

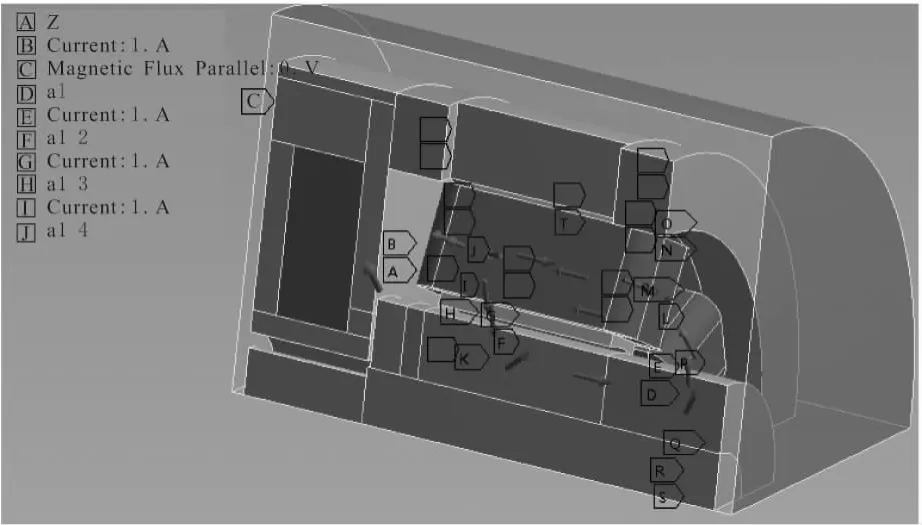
图4 磁场分析边界条件

3.3 优化过程

先通过DOE在结构参数变化范围内生成设计点，然后通过磁场有限元计算出每个设计点得目标参数的结果。为后续的灵敏度分析、响应面生成和优化计算奠定基础。各结构参数对电磁拉力的灵敏度关系如图5所示。

由灵敏度分析可知，对径向磁悬浮轴承磁拉力相对影响较大的是硅钢片铁芯厚度P1-H＿Fexin、硅钢片外环内径P3-R＿out2、硅钢片轴向宽度P5-H＿guigang；P8-H＿Cu和P15-Z1对它有负面影响。由此可见，影响径向磁悬浮轴承磁拉力的主要是硅钢片的结构参数，这与理论分析是相符的。对于径向磁悬浮轴承磁拉力相对影响较大的是轴向线圈压盖厚度P15-Z1和轴向线圈外壳厚度P19-Z2。

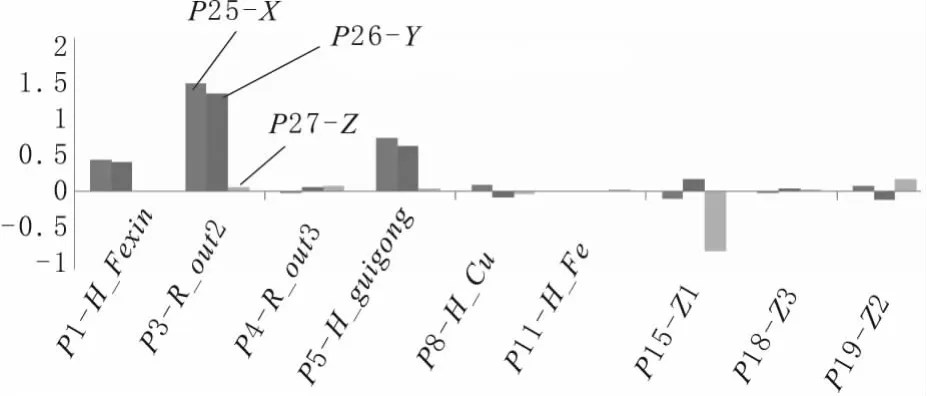
图5 各结构参数对电磁拉力的灵敏度关系

轴向磁悬浮轴承的结构参数对径向的磁拉力有一定的影响，同样，径向磁悬浮轴承的结构参数对轴向的磁拉力有一定的影响，这同样验证了两者磁场有一定的耦合。

4 多目标遗传算法优化解

调整各个参数的权重比，经过优化计算后推荐3组优化解，先通过磁场仿真验证推荐优化解的结果，后选取效果较好的那一组作为设计点，重新开始新一轮的优化计算。为了节省计算仿真时间可以略去对目标参数不太敏感的优化参数，反复优化直至到较好的优化解为止，如表3所示。

由表3可知，调整硅钢片的结构参数（硅钢片铁芯厚度、硅钢片外环内径、硅钢片外环外径和硅钢片轴向宽度）可以大大提高电磁拉力，将轴向推力盘厚度、轴向线圈压盖厚度和轴向线圈外壳厚度减小来提高轴向力等，这与理论分析是相吻合的。最后优化的结果如表4所示。

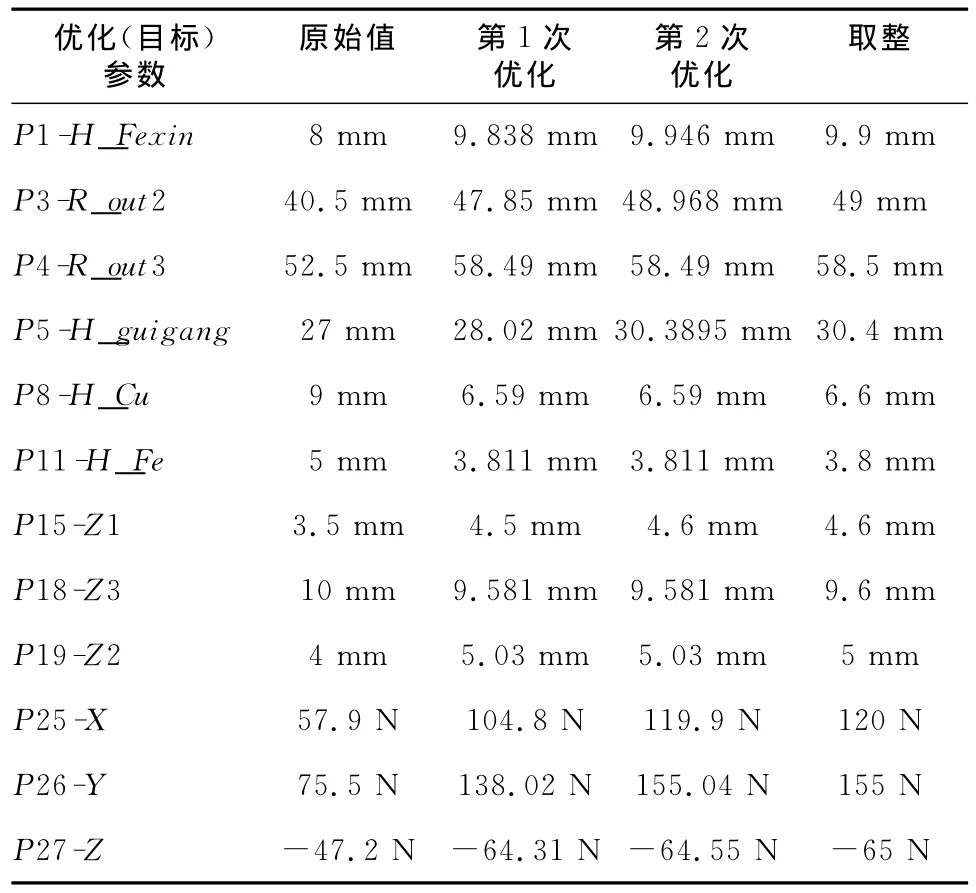
表3 磁悬浮轴承结构参数优化过程参数值

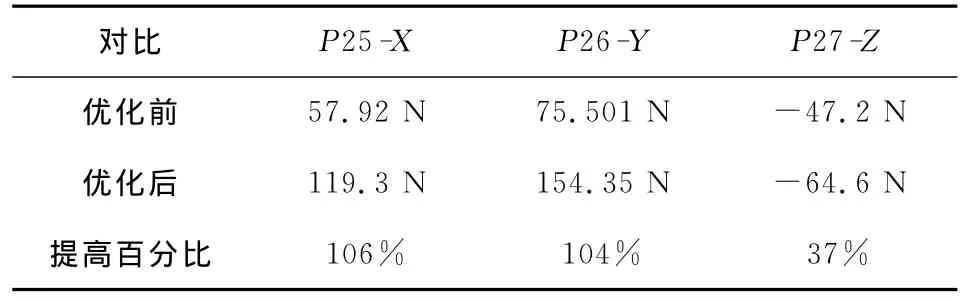
表4 磁悬浮轴承优化前后结果对比

5 结束语

通过对磁悬浮轴承结构参数的优化，在转子外径、工作气隙和工作电流不变的情况下，径向磁悬浮轴承单个磁极的静态吸引力和轴向磁悬浮轴承的静态吸引力得到了较大的提升。这对于磁悬浮轴承的承载力的提高是大有裨益的。但是此次优化分析，只对转子外径做了限定，对硅钢片外径没有限定，对线圈的大小也没有根据空间来自动调配。在实际运用中，硅钢片的外径和转子外径很有可能是限定的，磁悬浮轴承的承载力优化提升的空间就会压缩，然而对磁悬浮轴承的快速优化设计提供了参考依据。

［1］Fonseca C M，Fleming P J.Multiobjective Optimization and multiple constraint handling with Evolutionary algorithms-part I：A unified formulation［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part A：Systems and Humans，1998，28（1）：26-37.

［2］Goldberg D E，Richardson J.Genetic algorithms with sharing for multimodal function optimization［A］.Proceedings of the Second International Conference on Genetic Algorithms［C］.1987.41-49.

［3］Deb K，Goldberg D E.An investigation of niche and species formation in genetic function optimization［A］.in Proc.Third International Conference on Genetzc Algorithms［C］.Morgan Kaufmann，1989.42-50.

［4］高学金，王 普，孙崇正，等.基于 MOGA和SVM的发酵过程建模［J］.信息与控制，2006，35（1）：12-15.

［5］G施韦策，H 布鲁勒，A特拉克斯勒，著.主动磁轴承基础性能及应用［M］.虞 烈，袁崇军，译.北京：新时代出版社，1997.

［6］朱烷秋，张 仲，诸德宏，等.交直流三自由度混合磁轴承结构与有限元分析［J］.中国电机工程学报，2007，27（12）：77-81.

［7］Xie Zhi-yi，Zhu Huang-qiu，Sun Yu-kun.Structure and control of AC-DC three-degree-of-freedom hybrid magnetic bearing［A］.Proceedings of the 8th International Conference on Electrical Machines and Systems（ICEMS）［C］.Nanjing，2005.1801-1806.