基于盲源分离的无源雷达直达波提纯方法
张 瑜,陈丹丹,贺秋瑞
(河南师范大学物理与电子工程学院,河南 新乡 453007)
0 引言
无源雷达是指雷达本身不发射电磁波信号,而利用外辐射源 (如广播发射台、电视发射台、移动基站以及导航卫星等)发射的信号作为探测信号,通过接收经过目标反射的回波信号提取目标的方位、距离、速度等信息,来完成目标探测和跟踪的雷达系统。无源雷达因其抗干扰、反隐身、反辐射导弹、抗低空突防等诸多优点受到了雷达界的高度重视[1-3],各个国家都投入了大量的人力、物力对其进行研究。利用外辐射源信号进行目标探测和跟踪的关键技术是无源相干定位技术[4]。一般而言,无源雷达系统实现相干定位时在接收系统中设置2个通道,即接收目标回波信号的回波通道和接收直达波信号作为参考信号的参考通道。人们多是考虑抑制回波通道的直达波干扰,却较少关注参考通道中获取直达波的纯度,一般认为参考通道接收天线主瓣指向发射台,接收到的混合信号中直达波信号功率最大,干扰可以忽略。其实不然,在无源雷达系统中,直达波主要有2个作用:一是作为参考信号用于对消回波通道的直达波;二是作为参考信号与目标回波信号做相关检测[5]。此外,直达波信号的模糊函数定性地分析了该信号是否可以达到探测系统所需的距离分辨率和速度分辨率。因此,直达波信号的纯度对整个无源雷达系统来说尤为重要。
目前,一些信号处理手段已成功应用于直达波提纯[6-9]。时域上主要是自适应均衡、对消技术;在频域上主要有复倒谱技术和频域的动态补偿技术;在空域上主要是在多径杂波方向形成零陷来对其进行抑制,从而凸显直达波。但是以上这些技术的实现需要通道参数、波形参数、来波方向等先验知识,在仅只有接收数据的前提下,很难得到成功应用。因此,需要借助盲信号处理手段,目前采用最多的是恒模盲均衡以及其改进算法[10],虽然对直达波有很好的恢复效果,但是仅仅对特定的信号模型适用,限制了辐射源的选择。本文提出了只需要接收数据便可以实现直达波提纯的基于全局最优盲源分离算法[11]。该算法适用于零均值、不相关的线性混合信号且混合数据中最多只有1个高斯信号的分离,只需对混合数据进行数学计算,而不需要其他的先验知识,便可以到达分离提纯的目的。在无源雷达中,参考通道接收的混合数据,满足该算法的前提条件,因而该算法可以成功地应用于该系统的直达波提纯。
1 基于全局最优盲源分离的直达波提取
在无源雷达接收系统中,把直达波、多径信号以及噪声干扰分别看作各有1个辐射源产生,设源信号向量为S=(s1,s2,…,sn)T,各个辐射源对系统的贡献率称为源信号si。这些辐射源发射的信号在空间传输和接收机中以线性混合方式进行混合,这种混合方式通过1个混合矩阵H=(hij)N×N来实现。设接收机的混合数据向量为X,那么接收机接收到的数据可用X=H×S来表示,其中X=(x1,x2,…,xn)。要提取直达波就必须对混合信号进行分离,即找到1个分离矩阵W来恢复各个源信号,如式Y=WX,Y=y1,y2,…,yn,Y 为恢复的源信号向量。
1.1 全局最优盲源分离算法
在全局最优盲源分离算法中,首先建立目标函数。假设 C=[c1,c2,...,cn]T是 n 维非零向量,则恢复信号向量Y的分量y可表示为n个源信号的线性组合
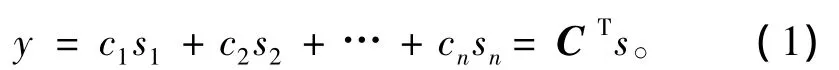
假设存在函数g,g(s1),g(s2),…,g(sn)不相关,并且满足
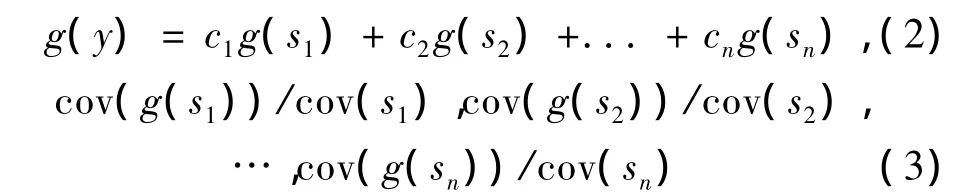
中各个元素互不相等,定义目标函数的一般形式为
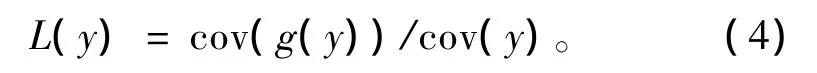
数学证明,源信号任意线性组合的目标函数值在宽松条件下小于最大的源信号的目标函数值。因为目标函数是关于分离矩阵W的二次型,所以W的全局最优求解转化为广义特征值的求解问题,用求出的广义特征值对应的特征向量构成的矩阵即为分离矩阵W。
定理1:假设源信号 s1,s2,…,sn互不相关,并且存在函数g满足式(4),则函数g(s1),g(s2),…,g(sn)是互不相关函数,并且 L(s1),L(s2),…,L(sn)互不相等。定义
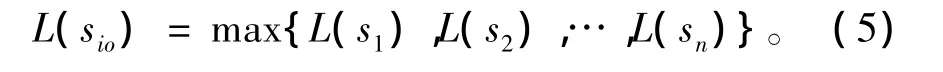
对于恢复信号y,有

当y≠asio时,a为非零常数,有
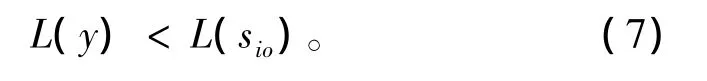
该定理的证明过程详见文献 [11]。
因此,可以通过最大化式(5)来恢复源信号sio,其中Y=WTX。当提取出来sio后,可以用同样的方法提取剩下的信号。最后得到分离矩阵同时恢复所有源信号。
因为L(si)互不相等,不失一般性,可假设

令wi为WT的第i行,根据定理1可得
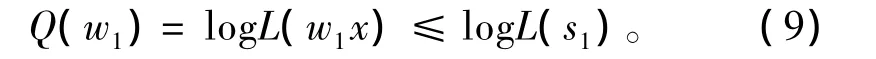
因为H是一个n维非奇异方阵,因此:
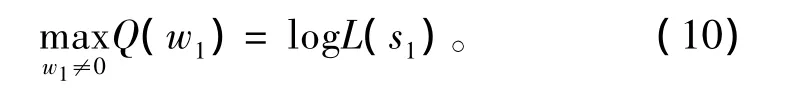
源信号s1可以通过求解式(10)的最优解来提取。对函数Q(w1)求梯度可得
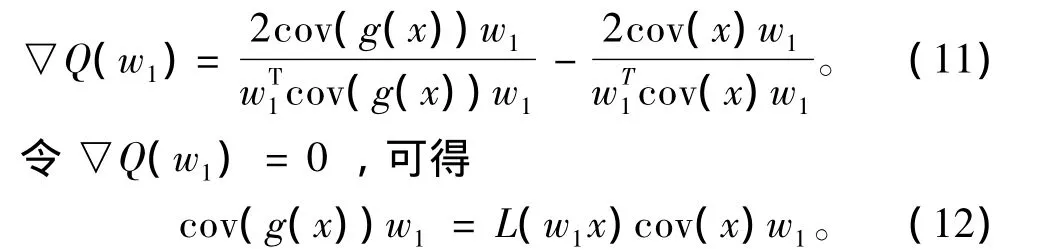
其中cov(x)和cov(g(x))都为正定矩阵。求解式(12)实际上变成求解广义特征值问题。通过求解,可得w1,在式(10)中是最大特征值对应的特征向量。显而易见,第二大特征值对应的是w2,第三大特征值对应的是w3,依次类推,第n大特征值对应wn。最后得到矩阵W。
针对函数g,假设每个恢复信号y都是时间t的函数,令
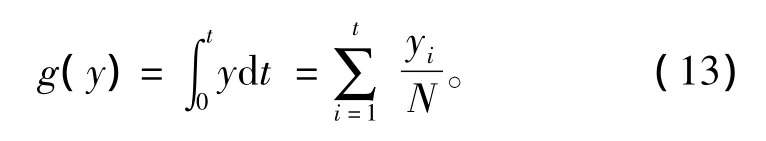
式中:N为采样数;yi为恢复信号向量Y的各个分量,i=1,2,…,n。可知,函数g满足上述分析的要求。将其代入式(11)可得
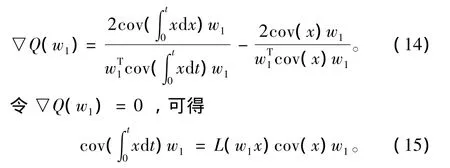
1.2 基于全局最优盲源分离算法的直达波提取方法
由于无源雷达接收机接收到的各组观测数据之间可能存在相关成分且均值不为0,因此在利用全局最优盲源分离算法之前,首先要对观测数据进行零均值处理和白化预处理,具体方法在文献[12]中有详细说明;其次,在观测时间内对观测数据进行积分,求出函数g(x);最后对观测数据求协方差以及g(x)的协方差代入式(15)求得特征值的特征向量,并组成分离矩阵W,从而对观测数据进行有效的分离。
2 仿真实验与分析
基于全局最优盲源分离算法在对参考信号中的直达波进行提纯时,只要满足该算法对数据要求的前提条件,均可应用该方法进行数据处理。因此该算法不局限于辐射源的选择。本文以基于调频广播辐射源的无源雷达系统为例来进行仿真实验。
在Matlab仿真环境下,编程实现全局最优盲源分离算法,采用模拟的调频广播信号为直达波信号,采样间隔设置为0.01 s,仿真时间为2 s。调制系数为200,载波为幅度是1的2000 Hz正弦波,产生一个类似的声音信号去控制调频信号,如图1所示;用不同的延时0.1 s,0.15 s,0.2 s,以及对应的衰减系数0.5,0.1,0.01模拟3条多径信号,选择加性高斯白噪声模拟接收系统中的噪声。如上所述,各有5个辐射源产生,随机产生5×5线性混合矩阵用来模拟空间混合方式以及通道混合参数。采用全局最优盲源分离算法对混合数据进行处理,提取直达波信号,如图2所示。对比图1和图2可知,全局最优盲源分离算法恢复出了直达波信号,虽然幅度改变了,但这不影响后续的相关处理效果。
直接用接收机接收到的混合数据进行模糊函数分析,如图3和图4所示。用提纯后的直达波进行模糊函数分析时,如图5和图6所示。
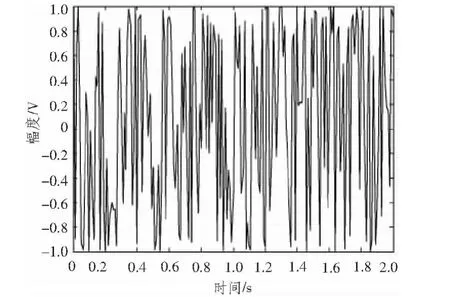
图1 调频广播的直达波信号Fig.1 Direct path wave signal of FM radio
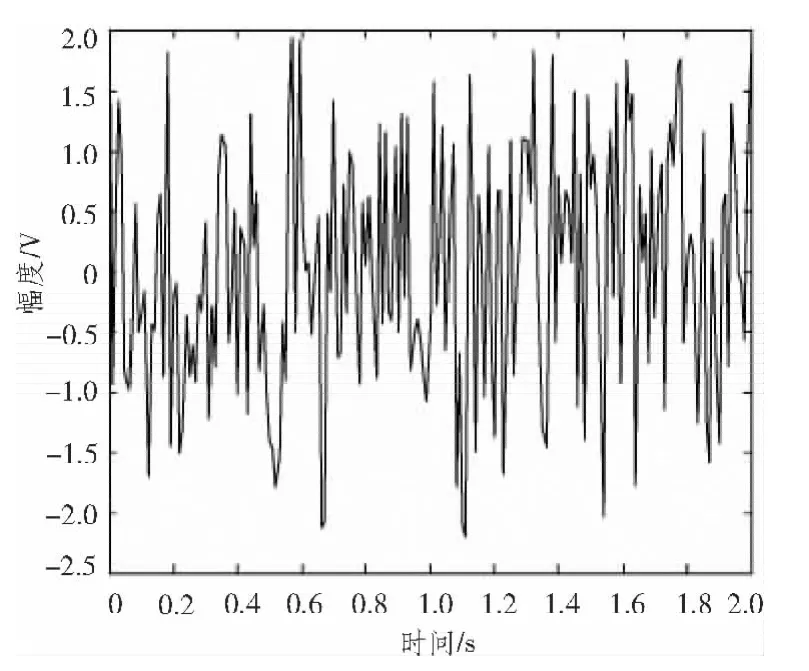
图2 提取的直达波信号Fig.2 Extraction of the direct path wave signal
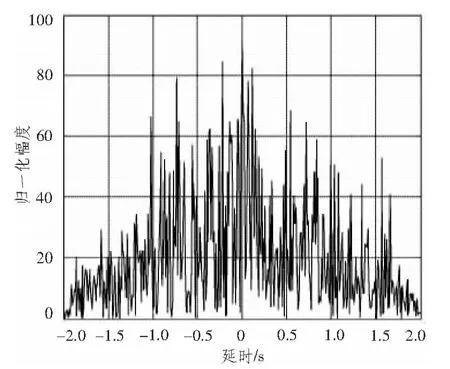
图3 混合数据的自相关函数Fig.3 Autocorrelation function of hybrid data
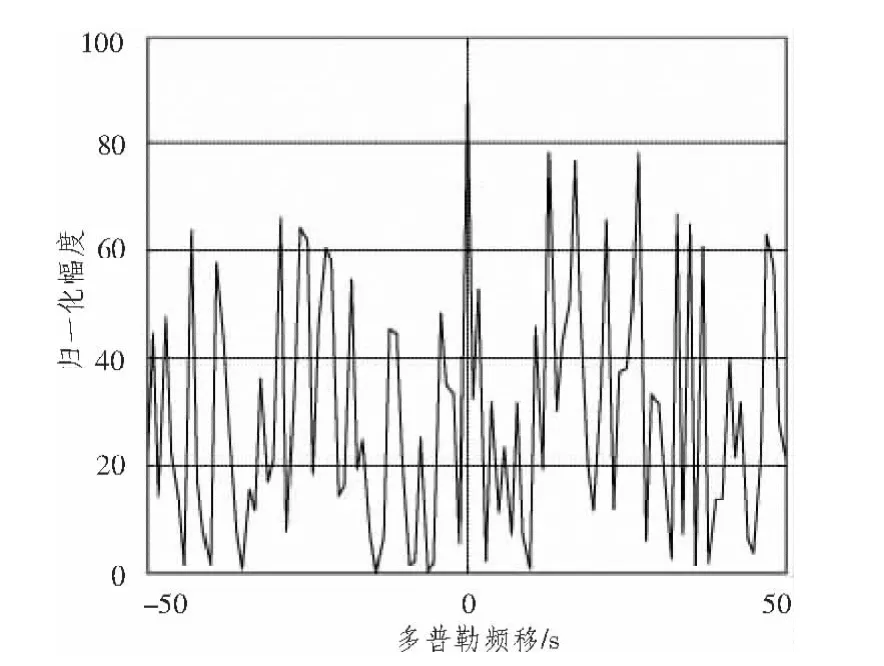
图4 混合数据的多普勒敏感度Fig.4 The doppler sensitivity of hybrid data
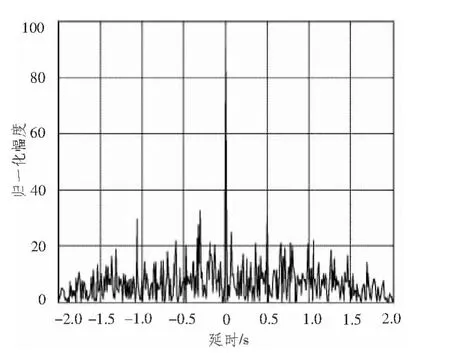
图5 提纯后的直达波自相关函数Fig.5 Extraction of the direct path wave autocorrelation function
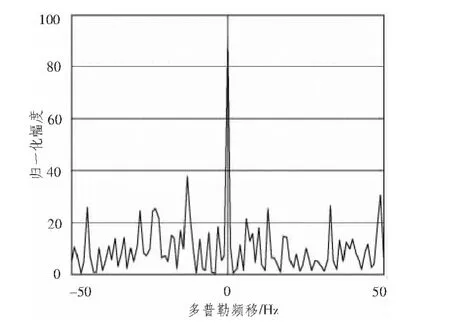
图6 提纯后的直达波多普勒敏感度Fig.6 Extraction of the direct path wave doppler sensitivity
对比图3、图4和图5、图6可以发现,提纯前,直达波由于受到多径杂波和噪声的干扰,使其自相关函数零时刻的尖峰受其他时刻尖峰的影响而具有模糊性,在多普勒域,由于旁瓣分布比较高,影响零时刻主瓣的判断,使多普勒敏感度下降。提纯后的直达波在距离和速度上的尖峰更加明显,因此具有较好的距离分辨率和速度分辨率,对系统的性能进行了很大程度的改善。
3 结语
本文首先分析直达波提纯的必要性,针对无源雷达系统接受到的混合数据特点,进而提出基于全局最优的盲源分离算法,用仿真实验进一步证明了该算法对直达波自相关函数的冲激特性的改善,在很大程度上提高了多普勒敏感度。对后续的目标检测的成功提供保障,因而对改善该无源雷达系统的探测性能具有重要的意义。但根据该算法所描述的需要逐个提取信号,最后把混合信号全部分离。虽然计算复杂度低,但会导致系统的实时性有所降低,并且增加了计算量,下一步工作需要改进。
[1]徐定杰,吕东泽,沈峰.基于改进子空间投影的无源雷达弱目标检测方法[J].宇航学报,2011,32(10):2228-2234.XU Ding-jie,LV Dong-ze,SHEN Feng.An improved subspace projection based method for weak target detection in passive radar[J].Journal of Astronautics,2011,32(10):2228-2234.
[2]吴海洲,陶然,单涛.基于DTTB照射源的无源雷达直达波干扰抑制[J].电子与信息学报,2009,31(9):2033-2038.WU Hai-zhou, TAO Ran, SHAN Tao. Direct-path interference suppression for passive radar based on DTTB illuminator[J].Journal of Electronics & Information Technology,2009,31(9):2033 -2038.
[3]左斌,赵洪立.无源探测雷达系统的现状及发展趋势浅述[J].中国科技信息,2009(14):52-53.ZUO Bin,ZHAO Hong-li.Elementary introdution of the developing situation and the further development of the passive detecting radar system[J].China Science and Technology Information,2009(14):52 -53.
[4]张财生,刘勤,唐小明,等.无源相干定位系统直达波干扰对消研究[J].现代雷达,2008,30(8):26 -28.ZHANG Cai-sheng,LIU Qin,TANG Xiao-ming,et al.Double-channel cancellation method for mitigating DPL in PCL[J].Modern Radar,2008,30(8):26 -28.
[5]王俊,赵洪立,张守宏,等.非合作连续波雷达中存在强直达波和多径杂波的运动目标检测方法[J].电子学报,2005,33(3):419 -422.WANG Jun,ZHAO Hong-li,ZHANG Shou-hong,et al.Detection of moving targets in commercial illuminator based radar system with strong direct signal and multipath clutters presented[J].Acta Electronica Sinica,2005,33(3):419 -422.
[6]杜东平,唐斌.基于频域对消的噪声调幅干扰抑制[J].电子与信息学报,2007,29(3):557 -559.DU Dong-ping,TANG Bin.A high performance algorithm of noise amplitude modulation interference suppression based on frequency domain cancellation[J].Journal of Electronics& Information Technology,2007,29(3):557-559.
[7]朱家兵,洪一.基于复倒谱技术的无源雷达直达波提纯方法[J].现代雷达,2007,29(8):75 -78.ZHU Jia-bing,HONG Yi.A direct-path-wave purified approach to passive radar on cepstrum technique[J].Modern Radar,2007,29(8):75 -78.
[8]吴海洲,陶然,单涛.数字电视辐射源雷达基于空域滤波的直达波获取[J].兵工学报,2009,30(2):226-230.WU Hai-zhou,TAO Ran,SHAN Tao.Direct-path signal obtaining to digital video broadcasting transmitter radar based on the spatial filtering[J].Acta Armamentarii,2009,30(2):226-230.
[9]李辉,何友,唐小明,等.非合作双基地雷达中直达波信号的重构[J].系统工程与电子技术,2010,32(10):2025-2030.LI Hui,HE You,TANG Xiao-ming,et al.Reconstruction of direct-path reference signals in non-cooperation bistatic radar[J].Systems Engineering and Electronics,2010,32(10):2025-2030.
[10]葛先军,何友,宋杰.基于改进CMA+MMA的直达波脉冲复包络估计技术[J].现代雷达,2010,32(12):54-59.GE Xian-jun,HE You,SONG Jie.Complex envelope estimation techniques of direct-path pulse signals using modified CMA+MMA[J].Modern Radar,2010,32(12):54-59.
[11]CHEUNG Y M,LIU H L.A new approach to blind source separation with global optimal property[J].Proceedings of the IASTED International Conference of Neural Networks and Computational Intelligence.Grindelwald,Switzerland,2004:137-141.
[12]张瑜,房少娟,李雪萍.低角雷达多径误差抑制盲分离方法[J].电光与控制,2011,18(10):32 -34.ZHANG Yu,FANG Shao-juan,LIXue-ping.Blind separation method oflow-angle radarmultipath error suppression[J].Electronics Optics & Control,2011,18(10):32-34.

