基于并行遗传混沌方法的UUV性能综合优化分析

陈 鹏，杨松林，刘福伟，俞 强

(江苏科技大学船舶与海洋工程学院，江苏 镇江 212003)

0 引言

UUV的设计要求一般包括水动力性能、操纵性、结构强度和稳定性、电力能源、低噪声、可制造性等，而且设计过程中的目标往往不止一个。就UUV性能优化设计而言，其本身就是一个多学科、多目标的优化问题。针对这类问题，根据设计任务书的要求，如何合理地确定目标函数、目标函数中各项性能指标的权重以及选择何种优化计算方法均是需要研究的问题。

在实际工程中，UUV设计的优化问题往往是按照顺序方式处理的，并未充分考虑各个学科之间的相互联系，所以传统的UUV优化设计工作得到的往往是局部最优解，并非全局最优解。目前，国内针对UUV的低阻、降噪、艇型、耐压壳等方面都已进行了单性能、单目标的研究，且已建立了较好的数学模型，并得到可靠的优化结果［1］。但是，包含多性能、多目标的综合优化研究工作尚处于起步阶段，无论是性能的综合优化，还是同时包含结构和性能的综合优化均需要进一步研究。

为了提供综合性能好的UUV设计，有必要进行其性能综合优化的研究。近年来，低阻力、小型化、远程化和操纵性好是UUV的发展趋势，而这些设计要求往往相互之间存在着制约的关系，如何在设计中综合协调以上矛盾，设计出综合性能优良的UUV，优化方法的构造是重要的研究课题［2－3］。本文从船舶快速性、操纵性和能源系统3个方面出发，构造UUV性能综合优化数学模型，将优化问题转化为求一个多目标、多变量、多约束条件的复杂数学极值问题。通过对艇体主尺度及相应参数的优化来进一步提升UUV的航行性能。除此之外，进一步分析目标函数类型及性能指标权重对该优化问题的影响，为UUV结构和性能的综合优化研究提供依据。

1 并行遗传混沌优化方法

遗传算法是基于达尔文自然界生物遗传及进化过程中“物竞天择、适者生存”的原理和遗传学的随机交换理论而发展起来的一种寻优方法。该算法具有解决复杂系统优化问题的能力。但在解决一些非常复杂的系统优化实际问题时，它一般具有很大的群体规模，从而使得算法的遗传进化运算过程进展缓慢，即耗时长、计算效率相对较低。应用实践表明，借助各种并行与遗传算法可不同程度地解决这个问题［4］。

本文构造一种并行遗传混沌优化方法，它借用计算机学科中的并行思想，将设计变量的区间进行等区域划分，每个设计变量的区间被分成几个区间块，各设计变量区间块的组合形成一个计算向量空间，假设设计变量的个数为N，划分的区间次数(又称为区间并行次数)为M，每个区间组合中优化计算次数为P，则形成区间的组合为MN种，总的计算次数

优化的区域本来是一个N维空间，并行思想实质是对区间的等区域分割，将计算空间进行缩小，因此能大大提高寻优的概率。由于计算的区间向量空间是并行次数的指数函数，所以区间并行次数不是越多越好，合理的选择区间并行次数和每个区间组内的寻优次数是决定并行算法优劣的关键。

分层并行遗传混沌方法的流程是:第一次载波采用非并行遗传算法，第二次载波采取并行的混沌算法，在第一次5个最优解的一定邻域内寻取最优解。

其中遗传算法优化基本过程是:首先采用某种编码方式将解空间映射到编码空间，每个编码对应问题的一个解，称为染色体或个体;其次通过随机的方法产生初始解 (被称为群体或种群)，在种群中根据适应值或者某种竞争机制选择个体;再次使用各种遗传操作算子 (包括杂交、变异)产生下一代 (下一代可以完全替代原种群，即非重叠性种群，也可以是替代原来种群中的一些较差的个体，即重叠种群)，如此下去，直到满足期望的终止条件。遗传算法中使用适应度这个概念来度量种群中的各个个体在优化过程中有可能达到最优解的优良程度。度量个体适应度的函数称为适应度函数，其定义一般与具体问题有关［5］。

混沌算法优化是通过混沌变量来实现的，最常用的方法是基于Logistic映射的混沌优化方法:

其中，μ为控制参数。不难证明，当μ=4时，式(2)处于完全混沌状态，除去奇点0.25，0.5，0.75之外的所有数值产生遍历，利用混沌对初值的敏感特性，迭代得到无穷多个0～1之间不同的初值(不动点除外)，将混沌变量的值映射到设计变量的空间得到相应的自变量的N维向量(N为自变量的个数)，代入目标函数进行寻找最优解［6］。

2 UUV性能综合优化数学模型

UUV性能综合优化包括快速性、操纵性及能源系统3个部分。本文分别选取需要分析的性能作为相应的指标，并将各指标通过幂指数积的方式构造成UUV性能综合优化目标函数，而将浮性、稳性、续航力等其他性能及设计变量的限制作为约束条件［7］。

2.1 设计变量

UUV性能综合最优可能性分布函数的计算问题较为复杂，涉及的艇型参数也很多。该优化UUV艇型参照挪威“HUGIN－3000”设计，为近似的回转体，其主艇体效果如图1所示。

图1 UUV优化模型主艇体的设计图Fig.1 The design drawing of optimization model of UUV

综合分析可得到29个设计变量:艇体首段长度Ld，艇体平行中体段长度Lp，艇体尾段长度Lr，艇体中横剖面直径D，艇体尾段端面直径Dr，艇体平行中体底部宽B，浮心纵向位置Lcb，螺旋桨直径Dp，螺旋桨盘面比Ae/A0，螺旋桨螺距比P/Dp，螺旋桨转速N，设计航速Vs，升降舵展弦比r1，方向舵展弦比r2，尾翼展弦比r3，升降舵面积s1，方向舵面积s2，尾翼面积s3，方向舵角，升降舵速率，能源舱长度Lpw，能源舱宽度Bpw，能源舱高度Hpw，能源舱电池长度方向的布置间距a，能源舱电池宽度方向的布置间距b，能源舱电池高度方向的布置间距c，能源舱外壳壁的厚度d，电池价格，钢板价格。

2.2 目标函数

设f(x)为总目标函数，Csp(x)为快速性指标，Cma(x)为操纵性指标，Cpw(x)为能源系统指标，则有:

式中:α＞0，β＞0，γ＞0，α·β·γ=1

各项指标的具体表达如下:

1)快速性指标

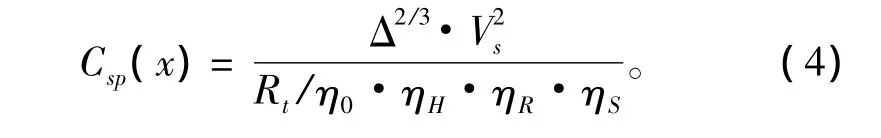
式中:Δ为排水量;VS为设计航速;Rt为总阻力;η0为螺旋桨敞水效率;ηH为船身效率;ηR为相对旋转效率;ηS为轴系传送效率。

2)操纵性指标

式中:β1＞ 0;β2＞ 0，β3＞ 0，β1·β2·β3= β;CH为水平面稳定性横准数;CRS为相对回转半径;Vχ为潜伏角速率［8］。

3)能源系统指标

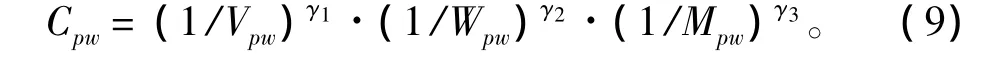
式中，γ1＞0;γ2＞0;γ3＞0;γ1·γ2·γ3= γ;Vpw为能源舱体积;Wpw为能源舱重量;Mpw为能源舱造价。

2.3 约束条件

2.3.1 等式约束

1)满足浮性条件，Δ保持不变

2)螺旋桨的推力与艇体航行时遭受的阻力相等

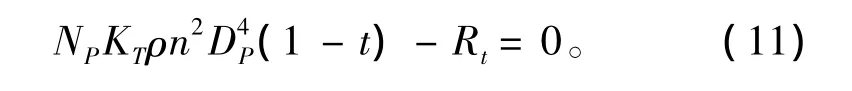
3)设计状态下主机供给螺旋桨的转矩与螺旋桨吸收的转矩相等

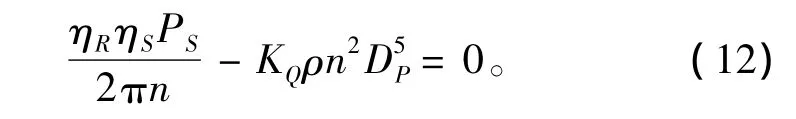
2.3.2 不等式约束

1)各个设计变量的取值范围。

2)续航力条件，5 kn速度航行下的续航力大于90 km。

3)直线自稳性约束:CH＞0。

3 优化计算及结果分析

3.1 初始条件

该UUV性能综合优化计算问题至少涉及29个设计变量，包括3个等式约束和2个不等式约束，若记入设计变量上下限约束，则不等式约束多达60个。显然，这是一个非常复杂的工程优化问题。作者采用上述的分层并行遗传混沌方法和数学模型编制了计算程序。

表1 设计变量范围Tab.1 The range of design variables

限于篇幅，在此仅以排水量约为3.3 t的UUV进行计算分析，该艇29个设计变量的初始范围如表1所示。

选取各指标权重如下:

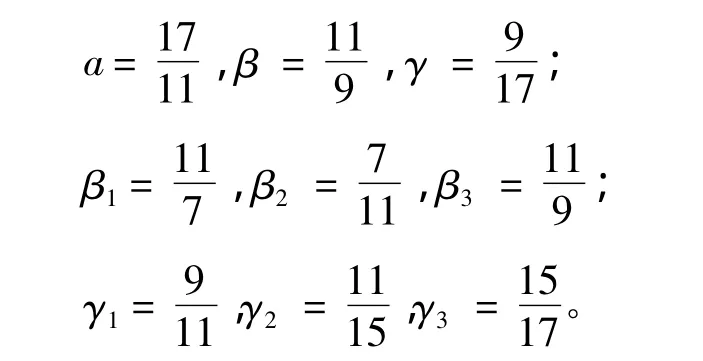
在一台计算机(主频2.80G Hz，内存3.49GB，硬盘1TB)上完成基于3000代遗传算法及5000次混沌算法的分层并行遗传混沌方法的算例优化计算。

3.2 优化计算

3.2.1 不同目标函数的计算

本计算的目的是通过目标函数的不同组成，探讨不同子目标函数对总目标及相应设计变量的影响［9］。计算过程时，将不参与探讨的性能指标权重设置为0，其余性能指标权重保持初始值不变，以快速性指标为基础，依次增加操纵性和能源系统指标，以分析新指标的加入对该优化问题的影响，每种情况计算3次，取最好值作为该种情况下的最终结果，计算结果见表2。

3.2.2 不同指标权重的计算

本计算的目的是:通过各性能指标权重的不同分配，分析性能指标权重对该优化问题的影响。由于各性能指标权重的乘积等于1，则各性能指标权重的改变成此消彼涨的变化趋势。所以在优化计算过程中，将对各性能指标权重的设置有所侧重，以分析不同性能指标权重对该优化问题的影响，计算结果见表3。

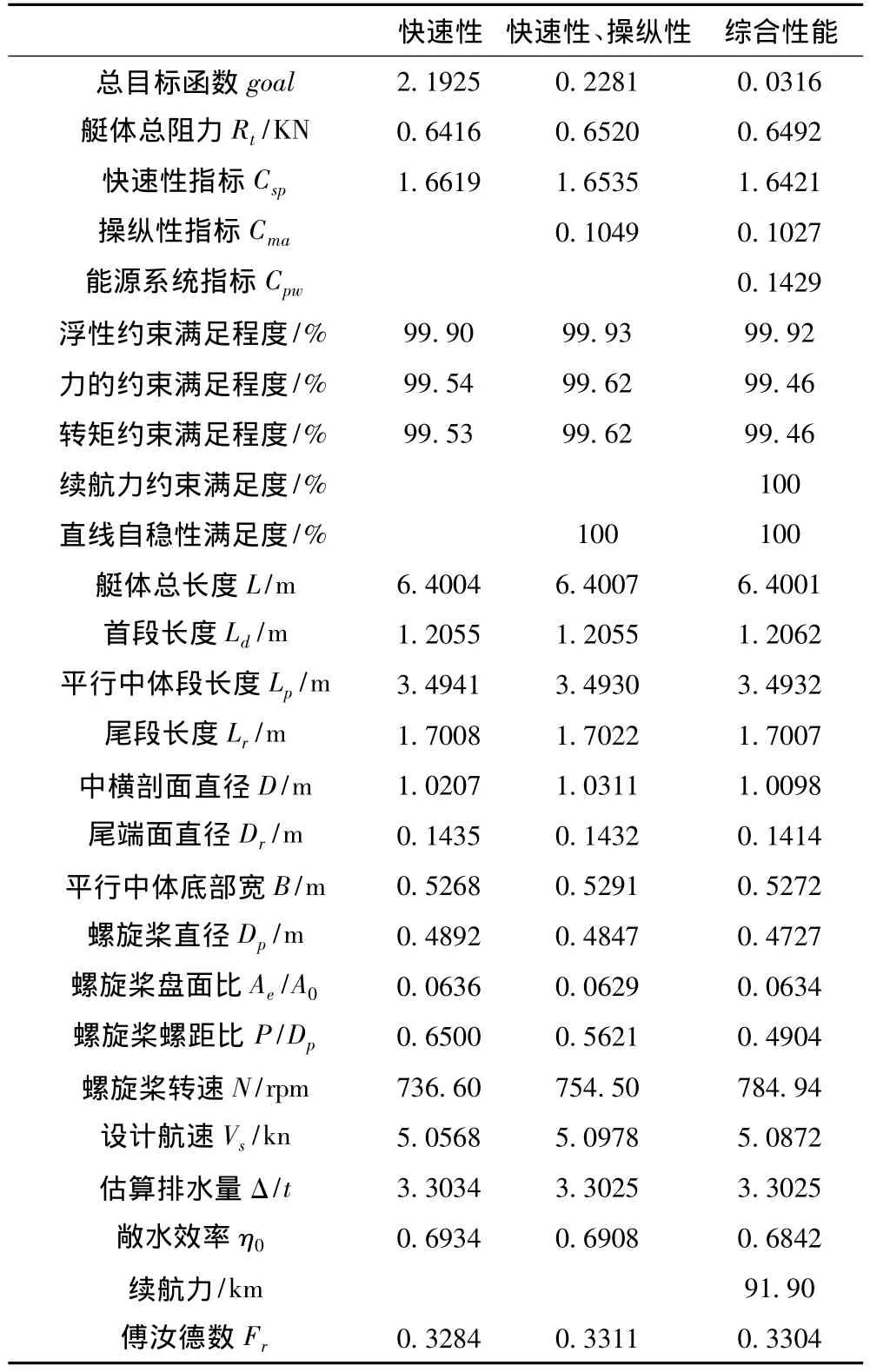
表2 不同目标函数的计算结果Tab.2 The calculation results of the different objective functions

表3 不同指标权重的计算结果Tab.3 The calculation results of the different index weights

本次计算3种权重方案，具体权重设置方案如下:

3.3 结果分析

通过计算，发现该并行遗传混沌方法在每种情况进行多次运算后，结果波动范围较小，等式约束的满足程度能达到99%以上，不过受性能指标权重的影响，有约束满足度未达到99%的情况出现，优化结果比较稳定。同时，不等式约束均获得100%的满足，说明优化方法计算精度高。除此之外，目标函数的不同和性能指标权重的改变，均对总目标函数有明显的影响，由于3种性能相互制约，所以其性能指标的变化并不是简单的线性变化，而是呈不规则的波动趋势。其余结论或建议如下:

1)通过不同目标函数的优化计算结果，发现随着综合优化性能指标的增加，总目标函数值有明显的波动变化，这主要是由于Cma和Cpw在目标函数的构成中占有一定的比例。同时，Csp呈相对稳定的递减趋势。在能源系统指标Cpw加入后，Cma也相对减小。除螺旋桨转速呈递增趋势外，大部分设计变量呈略微递减的变化趋势，其中以螺旋桨直径Dp和螺距比P/Dp相对明显。

2)对比性能指标权重分析的方案A和方案C:能源系统权重不变，随着快速性权重的增加、操纵性权重的减小，总目标函数、快速性指数、操纵性指数及能源系统指数均有所增大;对比性能指标权重分析的方案A和方案B，随着快速性权重的增加、操纵性和能源系统权重的减小，总目标函数、快速性指数和能源系统指标有比较明显的增大，操纵性指标减小。综上，说明性能指标和性能指标权重的变化趋势不一定相同。

3)通过以上计算结果可知，目标函数的构成及性能指标权重的设置均对该优化问题有明显影响。所以在UUV综合优化设计时，首先需要确定本次设计所需要考虑的性能指标，合理地将其构造成目标函数，并根据设计任务书的要求及航行区域的特殊环境，合理的设置各性能指标权重，这样才能得到综合性能佳的设计方案。

4 结语

本文从数学模型和优化方法2个方面研究UUV性能的综合优化问题。①从快速性、操纵性2个方面构造了UUV的性能综合优化数学模型;②将1种分层并行遗传混沌方法应用于UUV的性能综合优化问题中。计算结果表明，该方法计算结果好，且计算可靠、效率高。除此之外，本文从目标函数类型的不同和指标权重的改变2个方面对UUV性能优化问题进行分析。由于操纵性指标和能源系统指标与快速性指标不在同一数量级，其加以权重后，对总目标函数和相应指标均有比较明显的影响。同样，权重的改变对目标函数值和约束满足程度也有比较明显的影响，由于3种性能相互制约，所以其性能指标的变化并不是简单的线性变化，而是呈不规则的波动趋势。由于在实际生产设计中，需要考虑实际航行海况和设计任务书的要求，对各项指标的要求必然有所不同，所以如何更合理地选择性能指标权重是今后优化设计工作的重点。

［1］马伟锋，胡震.AUV的研究现状与发展趋势［J］.火力与指挥控制，2008，33(6):10 －13.MA Wei-feng， HU Zhen. Current researches and development trend on AUV［J］.Fire Control and Command Control，2008，33(6):10 －13.

［2］赵涛，刘明雍，周良荣.自主水下航行器的研究现状与挑战［J］.火力与指挥控制，2010，35(6):1 －6.ZHAO Tao，LIU Ming-yong，ZHOU Liang-rong.A survey of autonomous underwater vehicle recent advances and future challenges［J］.Fire Control and Command Control，2010，35(6):1－6.

［3］FLETCHER B.UUV master plan:a vision for navy UUV development［A］.OCEANS 2000 MTS/IEEE Proceedings［C］.Providence，RI，2000.

［4］李学斌.多目标遗传算法在水面船舶快速性优化设计中的应用［J］.江苏科技大学学报(自然科学版)，2008，22(5):1－5.LI Xue-bin.Application of multi-objective genetic algorithm to the optimal and fast design of surface ship［J］.Journal of Jiangsu University of Science and Technology(Natural Science Edition)，2008，22(5):1 －5.

［5］王建，王建华.标准遗传算法的研究进展［J］.华东船舶工业学院学报，2000(3):28－34.WANG Jian，WANG Jian-hua.Research fruit of traditional genetic algorithms［J］.Journal of East China Shipbuilding Institute，2000(3):28 －34.

［6］周晓，胡以华，陈修桥.混沌遗传算法及其在函数优化中的应用［J］.计算机与数字工程，2005，33(7):68－70.ZHOU Xiao，HU Yi-hua，CHEN Xiu-qiao.Chaos genetic algorithm and its application in function optimization［J］.Computer and Digital Engineering，2005，33(7):68 －70.

［7］张火明，杨松林，朱仁庆，等.船舶航行性能优化的模糊遗传算法［J］.中国造船，2002(3):7－15.ZHANG Huo-ming，YANG Song-lin，ZHU Ren-qing，et al.Fuzzy-genetic algorithm of ship navigation performance optimization［J］.Shipbuilding of China，2002(3):7 －15.

［8］施生达.潜艇操纵性［M］.北京:国防工业出版社，1995.SHI Sheng-da.Maneuverability of submarine［M］.Beijing:National Defence Industry Press，1995.

［9］杨松林，陈淑玲，张火明.船舶动力学性能及结构特性的综合优化方法［J］.中国造船，2006，47(2):10－16.YANG Song-lin，CHEN Shu-ling，ZHANG Huo-ming.Synthetical optimization method on ship dynamic performance and structure characteristic［J］.Shipbuilding of China，2006，47(2):10 －16.