舰艇真航向动态测量方法中舷角的误差修正及仿真
王 佳,王海波,陈荣娟,胡宏灿
(1.海军大连舰艇学院研究生管理大队,辽宁 大连 116018;2.海军大连舰艇学院航海系,辽宁 大连 116018)
0 引言
舰艇导航精度试验中航向真值的测量标定是重要组成部分。为实现舰艇航向的动态高精度测量,舰艇真航向动态测量方法研究主要采用计算方位和测量舷角相结合的舰艇真航向测量方案,即采用高精度定位设备所获取的舰位信息和被观测岸标位置点坐标计算出岸标的大地方位角,并采用电子经纬仪测量岸标的舷角,利用航向角、方位角和舷角三者之间的关系,解算出舰艇的真航向。
舷角的高精度测量因受到舰艇摇摆的影响会产生误差。误差修正方法主要有2种:一种是建立一个物理稳定平台,将经纬仪安装在平台上进行角度测量,但这种方法适用在舰艇摇摆较小的情况;另外一种是将经纬仪直接安置在舰艇甲板上,利用舰艇姿态信息进行数学方法修正,消除舰船摇摆的影响。本文主要分析舰艇摇摆对舷角测量的影响,尤其是较大幅度的摇摆对舷角测量的影响,针对第2种方法分析测量精度的改善效果。
1 舷角测量
舷角测量是通过在舰船甲板首尾线上架设电子经纬仪,电子经纬仪镜头瞄准首尾线舰首方向,水平度盘调零,再顺时针转动经纬仪望远镜瞄准岸标的来进行测量。由于受到风浪和涌的影响,舰艇会产生摇摆,因此电子经纬仪的水平度盘无法保持水平。为此,在实际测量时,要使电子经纬仪的水平度盘与甲板平面保持平行,这样电子经纬仪就只能测量到岸标相对于甲板坐标系的舷角和高度角。计算真航向时,会存在误差。
而岸标的舷角是在测者地面真地平面上,以舰艇航向线为基准,从航向线到岸标方位线之间的夹角。因此,必须将经纬仪所测量舷角投影到地平面上,即从甲板坐标系变换到地理坐标系,才能得到岸标的舷角。
2 相关坐标系定义及坐标变换原理
2.1 地理坐标系(t系)
取地理坐标系OXtYtZt为东北天坐标系,其原点设在运载体质量中心在地球表面的投影点O。Zt轴沿地心O'与坐标系原点的连线并指向天顶,垂直于当地水平面;Yt和Xt轴在当地水平面内,分别水平指北和水平指东,如图1所示。
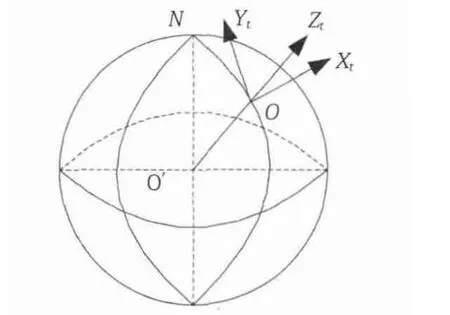
图1 地理坐标系示意图Fig.1 The schematic of geography coordinate
2.2 甲板坐标系(b系)
甲板坐标系OXbYbZb的原点位于舰艇质量中心,Yb轴与舰艇首尾线重合指向舰首方向,Xb轴与舰艇正横轴重合指向右弦,Zb轴与Xb和Yb轴构成右手直角坐标系,垂直甲板平面指向上方,如图2所示。
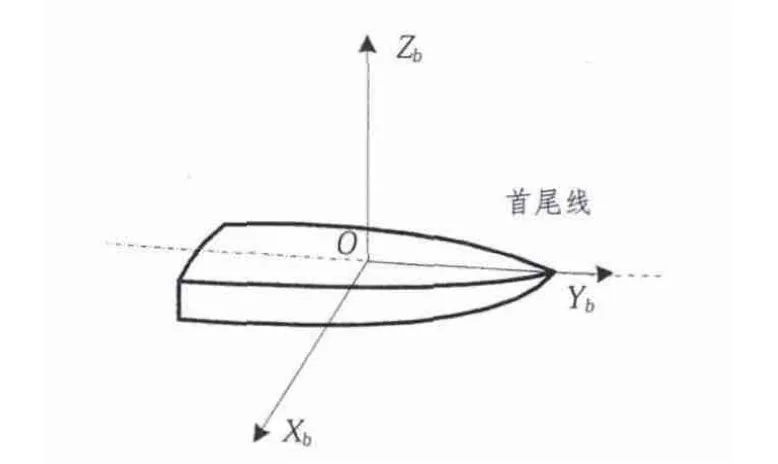
图2 甲板坐标系示意图Fig.2 The schematic of deck coordinate
2.3 坐标变换原理
舰艇甲板坐标系和地理坐标系之间存在着方位关系。若舰艇的首向角、纵摇角、横摇角分别用H,P,R来表示,那么就可以用(H,P,R)推导出2个坐标系的变换关系表达式。按照首向角、纵摇角、横摇角的定义,可按下列顺序分3次转动得到,如图3所示。
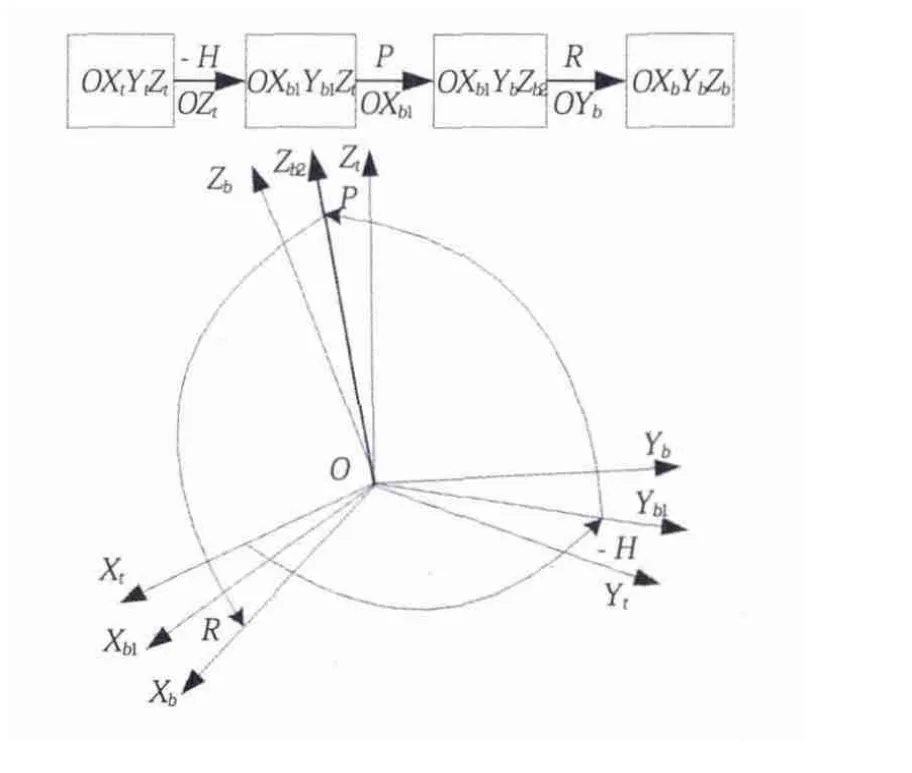
图3 地理系向甲板系变换示意图Fig.2 The schematic of coordinate transformation from geography coordinate to deck coordinate
设在初始时刻,甲板坐标系OXbYbZb与地理坐标系OXtYtZt相重合。根据欧拉角矢量变换相关理论,按顺序依次转动获得3个方向的余弦矩阵如下:
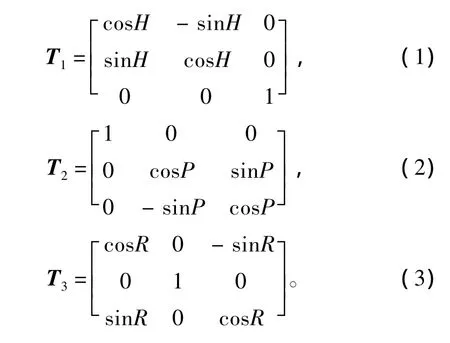
因此地理坐标系到甲板坐标系的坐标变换可以表示式(1)~式(3)3个方向余弦矩阵的乘积,但3个矩阵相乘时的排列次序应与甲板坐标系的转动次序相反,即:

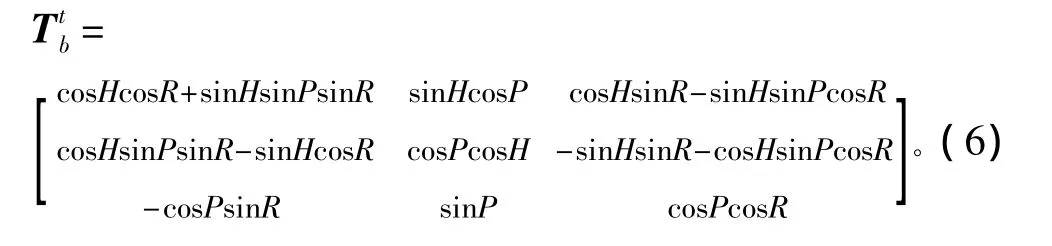
3 舷角测量误差补偿数学模型
设(A,h)为岸标大地方位角和高度角,(Q',h')为岸标甲板舷角和高度角,(H,P,R)为舰艇姿态角,(xt,yt,zt)为地理直角坐标值,(xb,yb,zb)为甲板直角坐标值。可得:

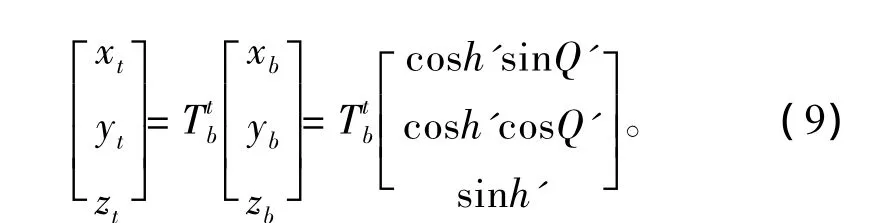
利用公式tanA=sinA/cosA=xt/yt可以计算得到:
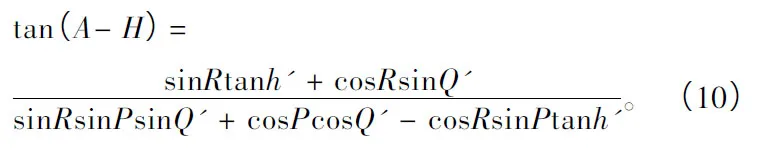
所以地理坐标系下的舷角为
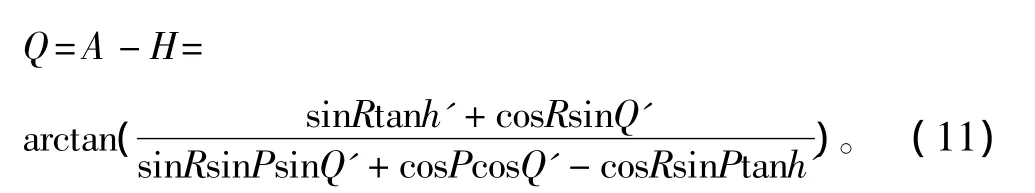
显然,真舷角与舰船纵横摇,及在舰艇上测得的岸标高度角和舷角有关。利用电子经纬仪测量出相对于甲板坐标系的岸标高度角、舷角,及舰艇实时提供的姿态信息,就可求出地理坐标系下的舷角。
4 仿真分析及结果验证
4.1 舰艇摇摆造成电子经纬仪对岸标测量的舷角误差和高度角误差分析
假设舰艇未发生摇摆,电子经纬仪有3组岸标的测量数据,如表1所示。

表1 无摇摆时经纬仪的测量数据Tab.1 The measurement data of board angle in the absence of warship swing
此外,在这里假设舰艇的摇摆有4种情况,纵横摇角度大小由表2给出。
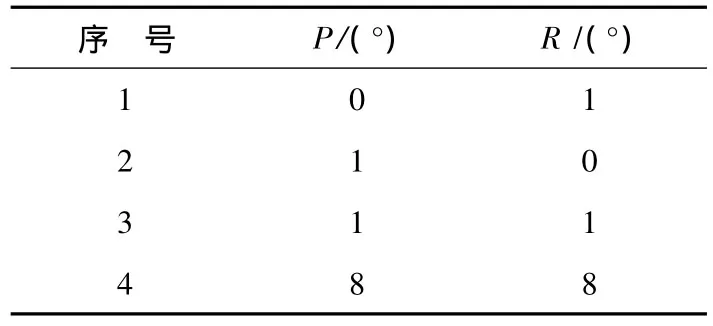
表2 四种舰艇摇摆情况下的纵横摇数据Tab.2 The data of pitch and roll in four cases of warship swing
对3组岸标测量数据分别按4种摇摆情况进行计算,由本文第2节相关原理求得公式如下:
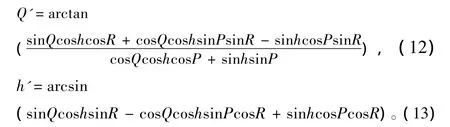
通过计算,得出12组摇摆造成电子经纬仪对岸标测量的舷角误差和高度角误差,如表3所示。
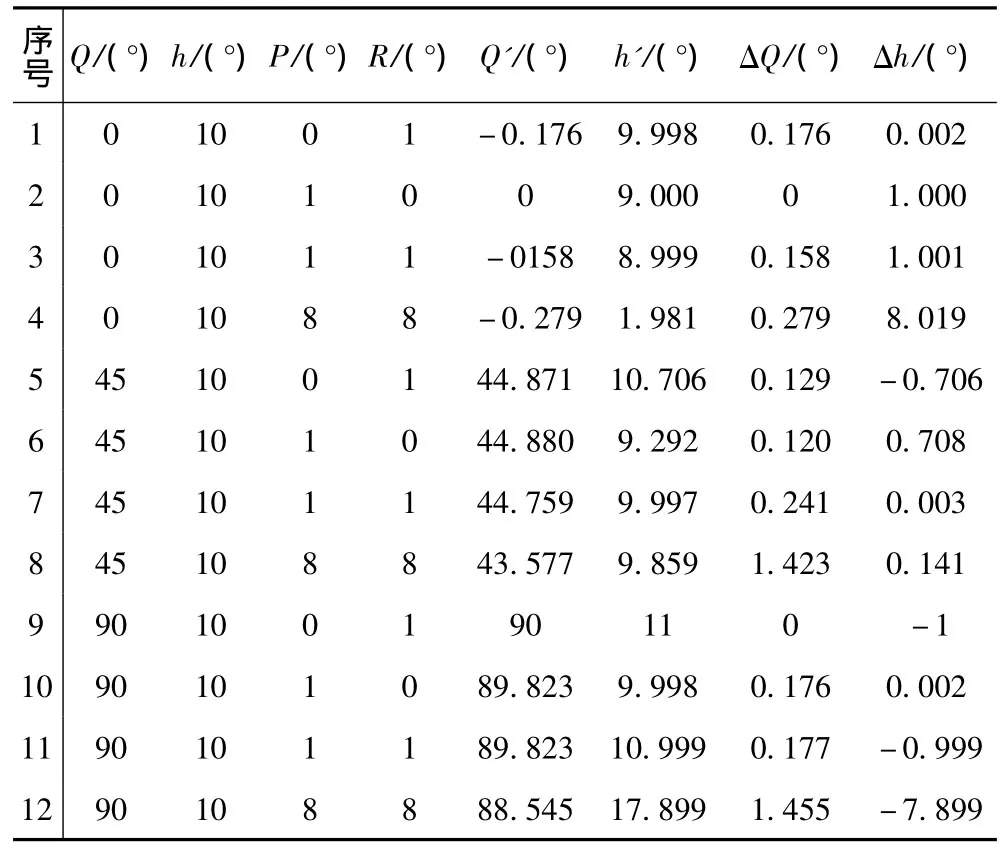
表3 四种舰艇摇摆情况下舷角、高度角测量及误差数据Tab.3 The measurement and error data of board angle and elevation angle in four cases of warship swing
表3中的Q'和h'为舰艇摇摆时经纬仪测量的岸标舷角和岸标高度角,ΔQ=Q-Q'和Δh=h-h'分别表示经纬仪测量岸标舷角和高度角的变化值。
由表3可见,舰艇摇摆使经纬仪产生了对准误差。其测量变化值不仅与舰艇摇摆的角度大小和方向有关,还与岸标相对于舰艇的位置有关。可见,在舰船摇摆状态下电子经纬仪测量受到影响,尤其摇摆角度变大时,测量会受到较大影响。
4.2 舰艇摇摆模型下舷角测量误差仿真
舰艇在海上航行中受到风浪的干扰而发生纵摇、横摇运动。为了模拟舰船海上的航行环境,假设舰艇纵摇角、横摇角的摇摆变化用下述模型简化描述:

式中:Pm和Rm分别为舰艇的纵摇角与横摇角变化的最大幅值;TP和TR分别为摇摆周期;ψP和ψR分别为纵摇、横摇的初始相位角;P0和R0分别为舰艇的初始姿态角。
为研究摇摆运动对舰载电子经纬仪测量精度的影响,建立3种简化舰艇摇摆模型,即模型Ⅰ (无摇摆状态)、模型Ⅱ (系泊状态)和模型Ⅲ (航行状态)。假设舰艇未发生摇摆时电子经纬仪测得的舷角Q和高度角h分别为45°和10°。舰艇的初始姿态角均为0,其他参数由表4给出。仿真步长Tn=0.1,仿真时间取100 s。通过Matlab编程仿真得到舷角测量误差曲线如图4所示。

表4 三种舰艇摇摆模型的各项参数Tab.4 The parameters of three warship swing models

图4 三种模型下的舷角测量的误差曲线图Fig.4 The error curve of board angle under the three models
通过分析图4得到,无摇摆状态和系泊状态下,纵横摇角度没有变化或变化较小,对电子经纬仪测量影响较小;航向状态下,纵横摇变化角度较大,对测量影响较大,需进行修正。
4.3 误差修正后舷角测量精度仿真验证
仿真条件:舰艇摇摆采用模型Ⅲ,电子经纬仪在舰艇上测得的舷角Q'和高度角h'值分别为43.577°和9.859°。纵摇 σP和横摇 σR精度均为3',经纬仪测量物标舷角精度σh'和高度角σQ'精度均为2″。仿真步长 Tn=0.1,仿真时间取100 s。
结合式(11),根据误差处理理论获得坐标变换后舷角测量精度公式如下:
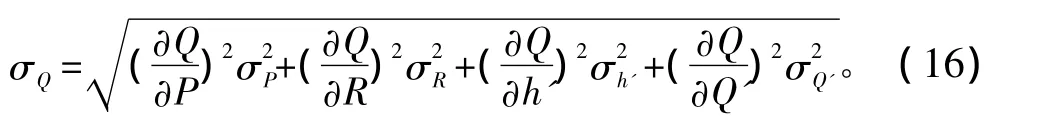
其中:
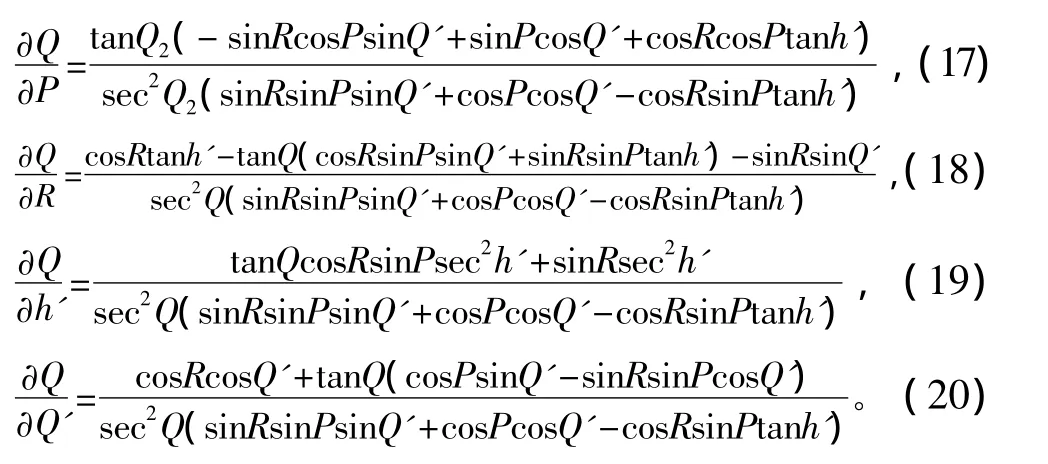
通过Matlab编程仿真得到坐标变换后舷角测量精度曲线。从图5可以看出,岸标舷角的测量值利用坐标变换原理从甲板坐标系转换到地理坐标系后,其测量误差得到很好的补偿。仿真表明坐标变换的误差修正模型可以应用在舷角测量中。

图5 坐标变换后舷角测量的精度曲线图Fig.5 The accuracy curve of board angle after coordinate transformation
5 结语
在航行过程中,舰艇受到风浪的影响,姿态角发生变化,进一步影响舰载电子经纬仪对岸标的舷角和高度角测量。本文为利用坐标变换原理和舰艇姿态信息推导出舷角测量的误差修正数学表达式,较好地改善了舰艇摇摆较大时对电子经纬仪测量的影响,保证了岸标舷角的测量精度,达到了理想的效果,对舰艇真航向动态测量方法研究起到重要作用。
[1]程禄,焦传道,黄德鸣.船舶导航定位系统[M].北京:国防工业出版社,1991.CHENG Lu,JIAO Chuan-dao,HUANG De-ming.Ship navigation and positioning system[M].Beijing:National Defense Industry Press,1991.
[2]张天光,王秀萍,王丽霞.捷联惯性导航技术[M].北京:国防工业出版社,2010.ZHANG Tian-guang, WANG Xiu-ping,WANG Li-xia.Strapdown inertial navigation technology[M].Beijing:National Defense Industry Press,2010.
[3]王有朝.对舰艇纵横摇坐标变换的讨论[J].现代雷达,2001(3):27-30.WANG You-chao.Discussion on coordinates transform of pitch and roll of warship[J].Modern Radar,2001(3):27-30.
[4]秦永元,朱新颖.舰载机捷联惯导自对准方案设计与仿真[J].中国惯性技术学报,2008,16(1):28 -33.QIN Yong-yuan,ZHU Xin-ying.Design and simulation on SINS self-alignment for carrier born aircraft[J].Journal of Chinese Inertial Technology,2008,16(1):28 -33.
[5]李恒德.在舰船处于浮态情况下进行作战系统对准[J].舰船工程研究,2000,69:15 -18.LI Heng-de.Combat system alignment when warship in the floating state[J].Ship Engineering Research,2000,69:15-18.
[6]杨丹,赵海滨.MATLAB从入门到精通[M].北京:中国铁道出版社,2013.YANG Dan,ZHAO Hai-bin.MATLAB from entry to the master[M]. Beijing:China Railway Publishing House,2013.
[8]张志远,罗国富.舰船姿态坐标变换及稳定补偿分析[J].舰船科学技术,2009,31(4):34 -40.ZHANG Zhi-yuan,LUO Guo-fu.Coordinate transformation of warship pose and analysis of stabilization compensation[J].Ship Science and Technology,2009,31(4):34 -40.
[9]丁振良.误差理论与数据处理[M].哈尔滨:哈尔滨工业大学出版社,2002.DING Zhen-liang.Error theory and data processing[M].Harbin:Harbin Institute of Technology Press,2002.
[10]葛兵,高慧斌.舰载经纬仪视轴自稳定方法研究[J].舰船科学技术,2006,28(6):93-94.GE Bing,GAO Hui-bin.Stabilization of LOS for carrierbased theodolite[J].Ship Science and Technology,2006,28(6):93-94.

